基于升階K 分布統計特征的超聲圖像增強技術

蔡潤秋

南京中醫藥大學附屬醫院 （江蘇 南京 210000）

超聲回波信號的統計分布呈現為給定組織結構平均回波強度附近的漲落。其中，漲落是由特定組織結構反射的超聲波的衍射和散射引起的，即使組織結構均勻分布，也會在圖像上呈現出散斑噪聲（speckle noise）[1]。在幾毫米尺度上，超聲成像的分辨率服從阿貝衍射極限，這限制了對超聲圖像中顯示的更精細組織結構的觀察。因此，全面了解超聲回波信號的統計分布對于提高超聲圖像的質量具有重要的意義。

現階段已存在幾種用來描述超聲回波信號的統計分布。例如，用于超聲回波信號的第一個統計分布——瑞利分布，該分布源自正態分布的二維擴展[1]，在瑞利分布模型中，散射元素在垂直和水平方向上均服從正態分布；但是，由于散射元素的數量不符合大數定律，或者給定組織中存在強散射元素，導致使用瑞利分布擬合超聲回波信號的精確度較低[2]。通過引入K分布，可以將超聲回波信號的統計描述推廣到非瑞利的統計分布，其最初是根據雷達制圖[3-4]發明的一種統計分布。同時被引入超聲回波信號擬合的還有用于描述通信噪聲的Nakagami 分布[5-7]。相對而言，上述統計分布并未足夠精確地描述超聲回波信號，其擬合精度有較大的改進空間。因此，基于散射回波的振蕩模式和隨機游走定理，升階K分布被提出用來模擬超聲回波信號。且相關研究表明，升階K分布以更高的精確度擬合了超聲回波信號的統計特性[8]。

升階K分布的函數結構由兩個參數定義，這些參數可由給定組織的統計特征決定。本研究發展了基于各種組織統計結構的統計熵值分析方法，通過利用不同組織區域的統計參數賦予該區域不同的權重。

1 基于升階K 分布統計特征的超聲圖像增強技術

為了評估各種組織結構的統計特性，本研究從商用超聲掃描儀VINNO 70的后臺數據庫中收集了幾個乳腺病變樣本和腎臟樣本的超聲回波信號，采集的數據是原始回波信號的數據，共包括100套乳腺病變回波信號，病變為3～4級乳腺腫塊[乳腺影像報告和數據系統（breast imaging reporting and data system，BIRADS）分級]，以及30套腎臟內緣區的超聲圖像樣本（正常組織），兩套數據均為數據矩陣的.rf 格式，直接保留了超聲回波的大部分未失真信息；并根據給定組織的結構選擇了感興趣區（region of interest，ROI）截取區域，每個ROI 截取區域包含相同數量的樣本點，以確保每次統計權重的計算是控制變量的（統計參量計算的精度與選取的樣本量有關），且歸集了ROI 內超聲回波信號的統計分布數據，并在Matlab 平臺上用升階K分布進行了擬合，最終生成了相應的統計參數。

通常情況下，小于超聲圖像分辨率極限的細節無法通過常規圖像處理算法確定，因為衍射漲落特征使來自給定ROI 部分的回波信號強度具有不確定性。然而，由于組織結構具有相同的統計特性，因此，通過上述統計分析方法分析超聲圖像，可為每個圖像像素提供統計加權，其中的統計權重由參數確定，而這些參數來自升階K分布的數據擬合。本研究將超聲圖像劃分為連續的10×10像素的小樣本區，并計算每個樣本區的統計參數（即統計權重），再通過這些統計權重重組出統計拓撲圖，即通過統計加權調整超聲圖像，每個樣本盒的灰度由其統計加權代替，見圖1。

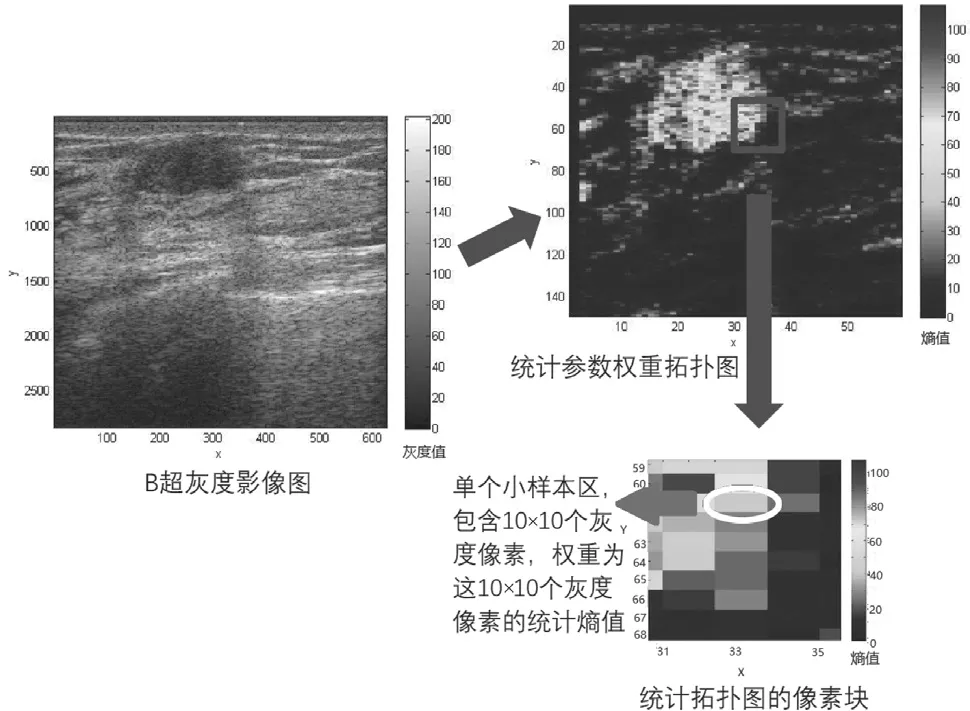
圖1 統計拓撲權重圖與小樣本區

由于超聲圖像的分割會降低分辨率，因此，應選擇盡可能小的樣本區。然而，隨著樣本區中包含像素數量的減少，樣本區之間的統計漲落會上升。統計漲落與小樣本區大小之間的關系為：ΔN=1/（N為每個樣本框中包含的元素數量）。

選擇熵為每個小樣本區的統計權重，從以下推導我們可以看出給定樣本區的升階K分布的參數與其熵有著密切的關系。

升階K分布[8]如下所示：

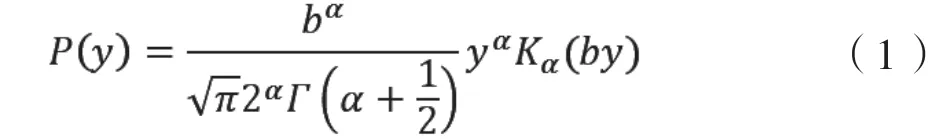
其中，y為圖像灰度值，P(y)為該灰度值的統計量大小；α為組織結構內散射體的聚集特征；b為散射信號的強度漲落；π為圓周率；Γ為Gamma函數；Kα為采用升階K分布的漸近形式作為近似值[9-11]：

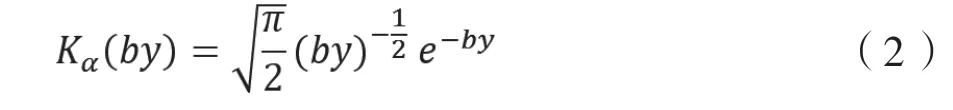
其中，e為自然對數。

則升階K分布可以表示為：

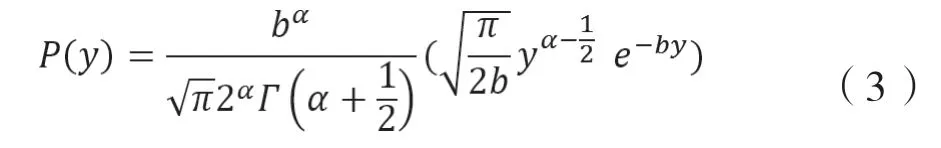
計算升階K分布的熵，以便將組織中樣本盒的統計參數與可推導的統計數量[12-14]聯系起來：

其中，S為樣本區熵值。

關于升階K分布的以上計算表明，任一樣本區的熵可以與其統計參數關聯在一起，因此，應用給定小樣本區的熵來繪制統計熵值權重圖是可行的。

2 基于升階K 分布統計特征的超聲圖像增強技術的應用

由前文可知，某些組織結構可以通過比原始灰度圖像具有更高對比度的統計熵值權重圖來區分。圖2A 所示的結構是原始超聲圖像中未明確確定的腎錐體部分，圖2B 為腎錐體的統計拓撲圖；圖2C為乳腺病變的超聲影像圖，圖2D 為乳腺病變的統計拓撲圖；由圖可以看出統計拓撲圖更加清晰地顯示了相關區域。根據超聲回波信號可以得出，病灶區域與正常組織之間的平均統計加權比約為1∶5，而原始圖像中病灶區域與正常組織之間的平均灰度比約為1∶3。統計熵值權重圖增強了各種組織結構之間的對比度。給定組織結構的特征在圖像細節低于衍射極限時變得模糊，從而降低超聲圖像的對比度；但局部漲落會在小樣本區的統計平均過程中消除，并以該小樣本區的統計參量（熵）反映組織結構信息，統計熵值權重圖顯示了隱沒于分辨率極限之下的信息。

統計熵值權重圖能夠更有效地識別病變組織，如乳腺腫塊組織。正常的組織結構可以自組織成一個有序的實體，因為熵隨著生物體的生長而減小[15-16]；病理變化扭曲了正常組織的有序結構，因此可以通過熵的變化對病變組織與正常組織進行區分[17-18]。由圖2可知，正常乳腺組織與乳腺腫塊組織之間的高對比度使臨床診斷達到更高的精確度。

圖2 乳腺腫塊和腎臟區域的超聲圖像與相應灰度圖像映射的統計熵值權重

統計熵值權重圖的視覺表達可以通過改變每個采樣箱中包含的元素數量進行調整。因為所含元素的數量越多，從統計上消除的噪聲和漲落越多，所以，具有較大取樣盒的統計熵值權重圖可提供更大的統計對比度，以區分病理特征與正常組織。增加小樣本區的尺寸亦存在缺點，即降低了統計熵值權重的空間分辨率，見圖3。

圖3 同一乳腺病變的統計熵值權重圖

統計拓撲圖對病灶和正常組織的區別能力和小樣本區的尺寸有著密切的關系，通常情況下，隨著單個小樣本區的尺寸逐漸增大（即小樣本區內包含了更多的數據點），統計漲落會被更好地平均，組織的特征統計參量會被更好地反映出來。因此，當小樣本區的尺寸增大時，統計拓撲圖中正常組織與病變組織之間的加權比會更高，即兩種組織的對比度會增強。

表1表示不同尺寸小樣本區正常組織與病變組織的對比度，由表可知，統計加權通過等高線圖或密度圖描繪并沒有區別，對比度的差異小于5%，表明在采用相同統計加權賦值原理的基礎上，圖形表現形式對區分組織差異的幫助較小；隨著小樣本區尺寸的增大，正常組織與病變組織之間的對比度差異上升，但在尺寸超過20×20后，對比度差異逐漸穩定，上升空間變得有限，考慮主要是由于當單個小樣本區內所包含的樣本足夠多時（此例為＞400），統計漲落已經被較好地消除，再增加樣本量對提升對比度的效果有限。圖4詳細說明了在密度圖模式與等高線圖模式下病變組織與正常組織的對比度，由圖可知，當小樣本區尺寸為1時，即按原像素狀況處理。

表1 不同尺寸小樣本區正常組織與病變組織的對比度（密度圖、等高線圖模式）

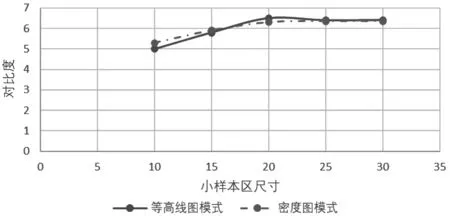
圖4 密度圖模式與等高線圖模式下病變組織與正常組織的對比度

3 小結

統計熵值權重圖的提出為病變組織結構的識別提供了另一種方法。基于統計熵值權重圖的圖像增強方法被證明是有效的，并且通過設置樣本區的大小可以調整統計熵值權重圖的組織間對比度。同時，增大小樣本區的尺寸可提高統計熵值權重圖的靈敏度，但當小樣本區的尺寸持續增大超過20×20時，統計權重的對比度收益下降，且統計熵值權重圖的分辨率也逐漸下降。