淺埋大斷面公路隧道施工工法對比研究
李長明
(中鐵十八局國際有限公司,天津 300000)
交通基礎設施建設直接關系到國家的經濟發展,因此各國都在積極開展交通建設。隧道因具有便利通行、節約時間等優點,在我國獲得大力發展。然而我國地質條件復雜,因此對隧道設計與施工的探討變得十分必要和迫切。
選擇合適的施工工法對隧道施工安全起至關重要的作用。眾多學者通過數值法、理論法、試驗法等對隧道施工問題展開了研究。李剛[1]以某大跨度隧道為研究對象,通過ABAUQS 有限元軟件建立三維模型分析了隧道施工全過程,研究了不同斷面隧道開挖中圍巖的受力變形規律。戚玉亮等[2]基于某大斷面淺埋暗挖海底隧道工程,利用數值模擬手段分析了采用CRD 法施工隧道圍巖的變形和受力情況,以及CRD 法施工的合理工序。陳林杰等[3]以超大斷面地鐵車站隧道為工程背景,通過PLAXIS 3D 有限元軟件建立數值模型,對比CRD 法和臺階法施工的圍壓變形和應力以確定合適的施工工法。李鵬飛等[4]通過理論法獲得隧道圍巖壓力的解析解,并對比分析不同圍巖參數和支護參數以確定該解析解的適用范圍。于麗等[5]針對淺埋黃土隧道工程,利用理論法研究了隧道圍巖壓力計算方法。李鵬飛等[6]通過對高地應力軟弱圍巖隧道施工現場監測,獲得了隧道施工中初期支護結構的受力變形規律,以位移和應力為指標分析了各施工工序的影響。鄧偉等[7]以某大斷面隧道為例,通過有限元軟件建立三維數值模型分析了大斷面隧道雙側壁導坑法施工過程,獲得了雙側壁導坑法過程下的隧道圍巖的變形規律和力學特性。
本文基于某淺埋暗挖公路隧道工程,利用有限元軟件建立隧道施工模型,分析不同施工工法下隧道圍巖和支護結構的受力變形,以獲得該工程最合理的施工工法。
1 工程概況
某公路隧道起訖里程DK78+464~DK8+253,線路經過山區,兩側地勢差異較大,山間谷地發育,局部有丘陵及河流階地分布。山體受斷裂及褶皺構造的制約,大多呈北東走向,地形較陡峻,地面標高200~700 m。地表大多植被茂密,除人工開挖外,基巖裸露地表少見,部分地段水土流失嚴重。沿線河流與山脈的延伸方向受構造線控制,并與構造線走向基本一致;河谷形態多為“V”型。
沿線地層出露較為復雜,一般上部為素填土、黏性土、粉土類、網紋狀、蠕蟲狀黏土等,下部為砂礫層、卵礫石層等,其中河流漫灘、谷地區等積水低洼地帶含淤泥、淤泥質黏性土等,第四系地層厚度5~30 m 不等,最大厚度達50 m。下覆地層巖性一般為砂質泥巖、頁巖、砂巖、礫巖、砂礫巖、灰巖、白云質灰巖、板巖、千枚巖、凝灰巖、變質砂巖等,并發生區域變質作用。
2 三維有限元模型
2.1 有限元模型
根據工程實際,建立160 m(寬)×60 m(縱深)×90 m(高)的模型(見圖1)。隧道橫截面為單拱大斷面,寬25.8 m,高19.5 m,隧道拱頂距地表12.5 m。在建模中未設置地下水,初始應力場即為自重應力場,在模擬隧道開挖形成的真實應力場時選用Null 模型。隧道周邊圍巖假設為各向同性的連續介質,用8 節點6 面體單元模擬,本模型為摩爾-庫倫。初襯結構用Shell 單元模擬,鋼拱架用Beam 單元模擬,錨桿用Cable 單元模擬,其余部分用實體單元模擬。

圖1 模型整體
2.2 模型參數選取
依據現場勘察資料,可知巖土體的物理力學參數(見表1)。

表1 土體參數
依據隧道設計方案,隧道結構物理力學參數如表2 所示。其中初襯混凝土等級為C25,二次襯砌混凝土等級為C40,鋼支撐選用工字鋼。
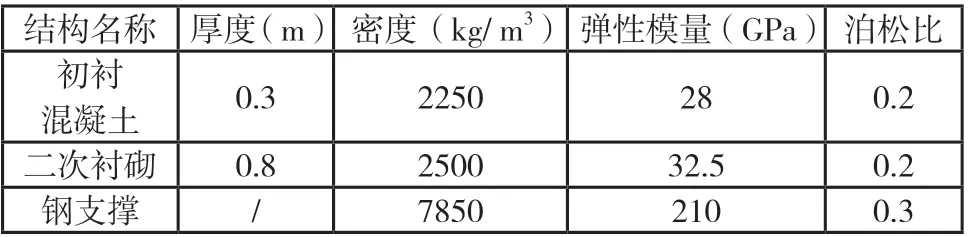
表2 隧道結構參數
2.3 不同施工方法模擬過程
2.3.1 三臺階法開挖模擬
以三臺階法開挖隧道需將隧道橫斷面由上至下分三個臺階依次開挖,以此循環。開挖進尺均為2 m,臺階長度為4 m。每次開挖完成后實施初期支護,下臺階掘進16 m 后進行二次襯砌,單次施工二次襯砌長度為4 m(三臺階法模擬見圖2)。

圖2 三臺階法
2.3.2 CRD 法開挖模擬
CRD 法開挖隧道時,將隧道橫斷面分為左右兩部分,各部分從上至下又分為3 個臺階。先從上至下開挖左側3 個臺階,隨后同樣方式開挖右側。每次開挖進尺均為2 m,臺階長度均為4m。每次開挖完成后實施初期支護,右側下臺階掘進16 m后進行二次襯砌,單次施工二次襯砌長度為4 m。CRD 法模擬如圖3 所示。

圖3 CRD 法
2.3.3 雙側壁導坑法
雙側壁導坑法開挖隧道時,將隧道橫斷面從左到右依次分為:左導坑、中間核心土和右導坑,再將每部分從上至下分為上中下三部分。首先依次開挖左導坑上中下三部分,接著同樣方式開挖右導坑及中間導坑。開挖進尺均為2 m,臺階長度為4 m。每次開挖完成后實施初期支護,右導坑最下部分掘進16 m 后進行二次襯砌,單次施工二次襯砌長度為4 m。雙側壁導坑法模擬如圖4 所示。
圖4 雙側壁導坑法
3 數值模擬結果及分析
3.1 三臺階法結果分析
3.1.1 圍巖位移
截取三臺階法施工下隧道正中間剖面豎向和水平位移云圖(見圖5),并給出相應隧道圍巖位移表(見表3),可見:隧道豎向位移峰值發生在隧道拱頂處,水平位移峰值發生在兩側邊墻處。隨著施工推進其周邊圍巖位移逐漸持續增大。隧道拱頂的最終豎向位移為-21.2 mm,隧道邊墻的水平位移呈對稱狀態且最終水平位移為9.2 mm。
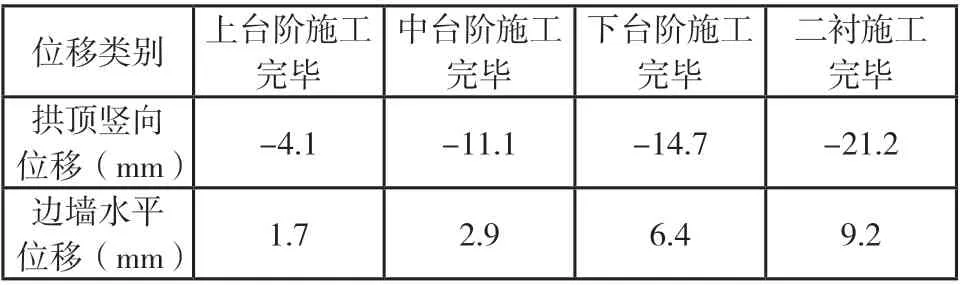
表3 三臺階法施工隧道圍巖位移
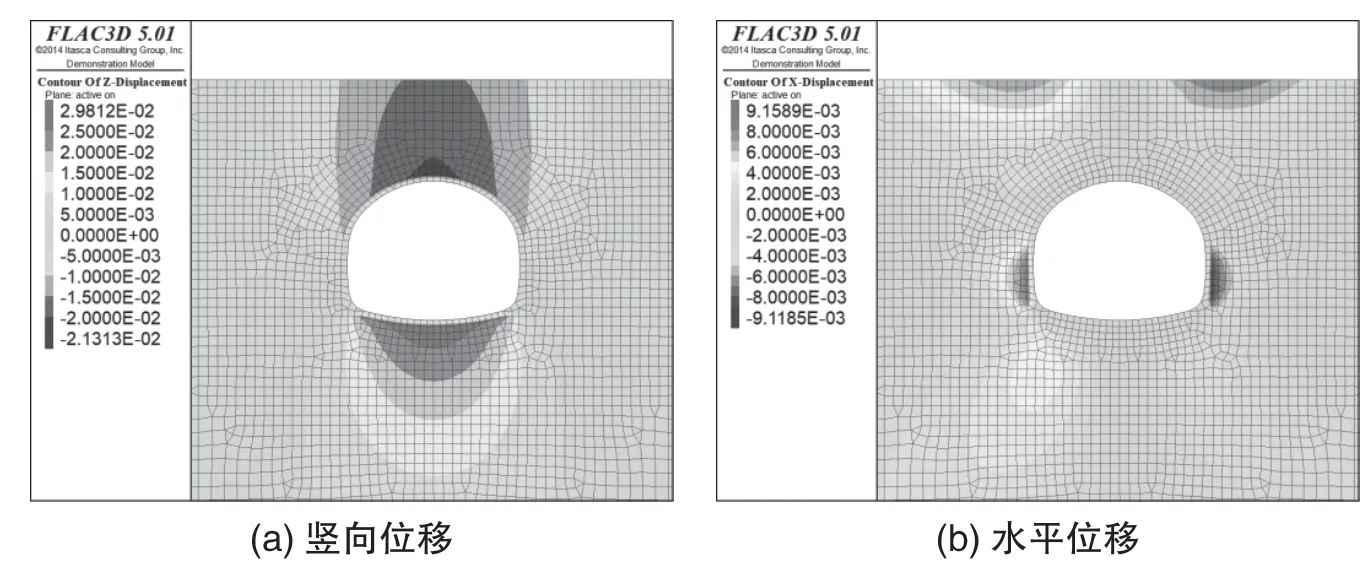
圖5 隧道正中間剖面的豎向和水平位移
3.1.2 鋼拱架受力
由隧道開挖完成后鋼拱架的應力云圖(圖6)可知,由于模型的對稱性,鋼拱架的應力左右兩側呈對稱分布,且沿著拱腳到墻角方向逐漸變大。應力較大值主要發生在隧道拱腰和拱頂位置,其中鋼拱架應力峰值發生在兩側拱腰位置,約為62.2 MPa,低于鋼拱架鋼材本身的抗壓強度,鋼拱架整體處于安全狀態。

圖6 隧道開挖完成后鋼拱架應力
3.1.3 初襯混凝土最大主應力
由隧道開挖完成后初襯混凝土的最大主應力云圖(圖7)可知,初襯混凝土的最大主應力為正,處于受拉狀態,且最大主應力沿著拱頂向拱腳呈現先變小后增大的狀態。由于對稱性,最大主應力同樣左右對稱,隧道仰拱和拱頂處的最大主應力比較大,原因為該處變形量比較大。根據工程經驗,初襯混凝土在隧道拱頂處受拉破壞對隧道安全性的影響比在仰拱處受拉破壞引起的影響更為顯著。因此在實際施工時,應著重監測拱頂的變形受力,及時采取有效的支護措施。

圖7 初襯混凝土最大主應力
3.2 CRD 工法結果分析
3.2.1 圍巖位移
由表4 (CRD 法施工過程中隧道圍巖位移對比)可見,隨著隧道逐步開挖,圍巖位移同樣持續增大。當左導坑施工完畢后拱頂豎向位移僅為-0.9 mm,初期支護后拱頂豎向位移卻迅速增大到-9.1 mm,可見圍巖拱頂豎向位移主要發生在右導坑施工后,此過程增加的豎向位移約占最終位移的72%,拱頂最終位移為-12.6 mm。左導坑施工完畢后邊墻水平位移為3.4 mm,初期支護后邊墻水平位移為5.1 mm,最終邊墻水平位移為5.5 mm,可見邊墻水平位移主要發生在左導坑施工過程中。
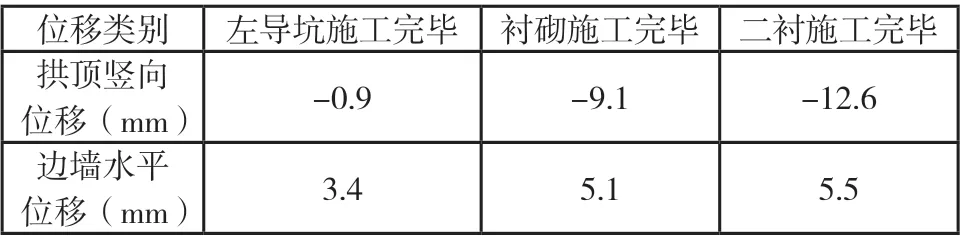
表4 CRD 法施工隧道圍巖位移對比
3.2.2 鋼拱架受力
由隧道開挖完成后鋼拱架的應力云圖(圖8)可知,鋼拱架應力均小于零,即處于受壓狀態。鋼拱架左邊部分應力大于右邊部分,原因是左導坑先施工。鋼拱架最大應力發生在豎向臨時支撐處,約為-92 MPa,低于鋼材本身的抗壓強度,鋼拱架整體處于安全狀態。
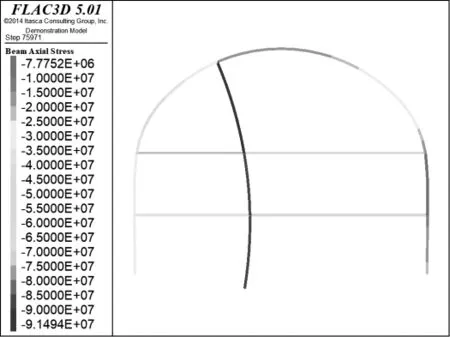
圖8 隧道開挖完成后鋼拱架應力
3.2.3 噴射混凝土受力
由隧道開挖完成后初襯混凝土的最大主應力云圖(圖9)可知,CRD 工法下初襯混凝土同樣處于受拉狀態。施工完成后,最大主應力較大值主要發生在隧道仰拱右側和拱頂右側,這是因為左導坑先施工導致豎向臨時支撐產生的支護作用更偏向隧道左半部分。
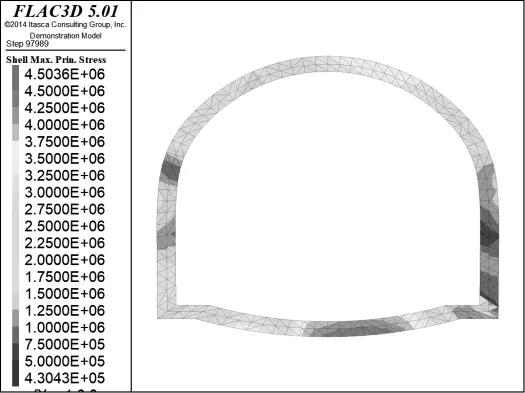
圖9 初襯混凝土最大主應力
3.3 雙側壁導坑法結果分析
3.3.1 圍巖位移
由表5(雙側壁導坑法施工過程中隧道圍巖位移狀況)可知,隨著隧道的開挖,圍巖位移變化規律相似。當右導坑施工完成后圍巖拱頂豎向位移僅為-0.9 mm,當中間核心區施工完成后拱頂豎向位移迅速增至-5.1 mm,可見圍巖拱頂豎向位移主要發生在中間核心區施工后,約占最終位移的54%。左導坑施工完畢后邊墻的水平位移為3.13 mm,右導坑施工完畢后其值為4.4 mm,中間核心區施工完后其值為4.9 mm,最終邊墻水平位移為5.1 mm,可見邊墻水平位移主要發生在左導坑施工中。
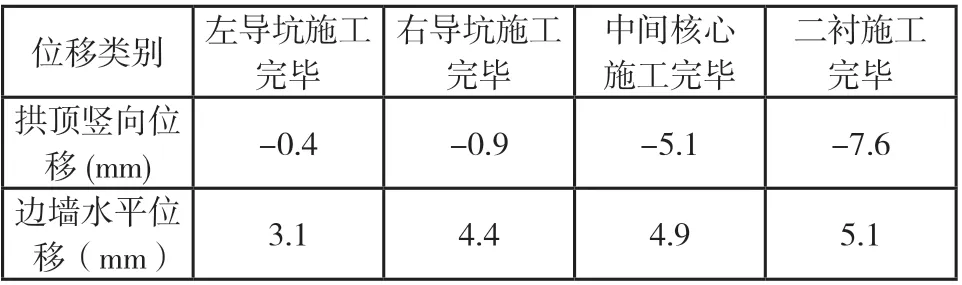
表5 雙側壁導坑法施工隧道圍巖位移
3.3.2 鋼拱架受力
由隧道開挖完成后鋼拱架的應力云圖(圖10)可知,鋼拱架施工完成后處于受壓狀態。施工完畢后,上部分橫撐處于受拉狀態,拉應力約為14.7 MPa,這是因為豎向臨時支撐存在向內部的水平變形。整個鋼拱架最大應力發生在豎向臨時支撐,峰值約為-136 MPa,同樣低于鋼材本身的抗壓強度,鋼拱架整體處于安全狀態。
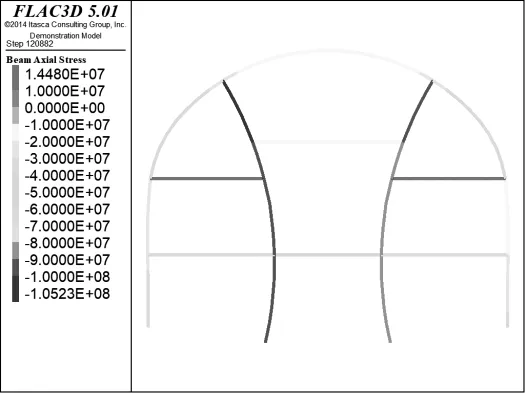
圖10 隧道開挖完成后鋼拱架應力
3.3.3 噴射混凝土受力
由隧道開挖完成后初襯混凝土最大主應力云圖(圖11)可知,雙側壁導坑法施工下初襯混凝土同樣處于受拉狀態,施工完畢后最大主應力在隧道拱頂位置較大,因此該工法施工時應著重監測拱頂的變形受力情況并及時支護。

圖11 初襯混凝土最大主應力
3.4 三種施工工法對比分析
由上述三種施工工法下不同位置的最大主應力曲線(取正中間剖面的計算結果,下同)(圖12(a))可知,不同施工工法下隧道圍巖最大主應力規律相似,四個位置最大主應力均小于零,即為壓應力。邊墻處的主應力值最大,拱腰處次之,仰拱處較小,拱頂處最小,其中圍巖仰拱和拱頂位置主應力較小,處于應力松弛狀態。對比不同工法下的主應力可知,雙側壁導坑法施工完畢后圍巖各處位置的最大主應力最大,圍巖受力狀態最佳。
由不同工法下拱頂豎向位移和邊墻水平位移曲線(圖12(b))可知,三臺階法下拱頂豎向位移和邊墻水平位移分別為21.3 mm 和9.2 mm,CRD 法為12.6 mm 和5.6 mm,雙側壁導坑法為7.9 mm 和5.1 mm。可見,雙側壁導坑法能更好地控制圍巖變形,三臺階法對圍巖變形控制的效果最差。
由不同位置處初襯混凝土最大主應力曲線(圖12(c))并對比三種施工工法可知,不同工法不同位置下的初襯混凝土最大主應力均大于零,即為拉應力。仰拱處的最大主應力最大,拱頂處次之,拱腰處較小,邊墻處最小。對比不同工法可知,雙側壁導坑法施工不同位置最大主應力均最小,由于混凝土材料的抗拉強度低,因此采用雙側壁導坑法時初襯結構受力狀態更佳,更有利于隧道施工過程中圍巖的穩定。
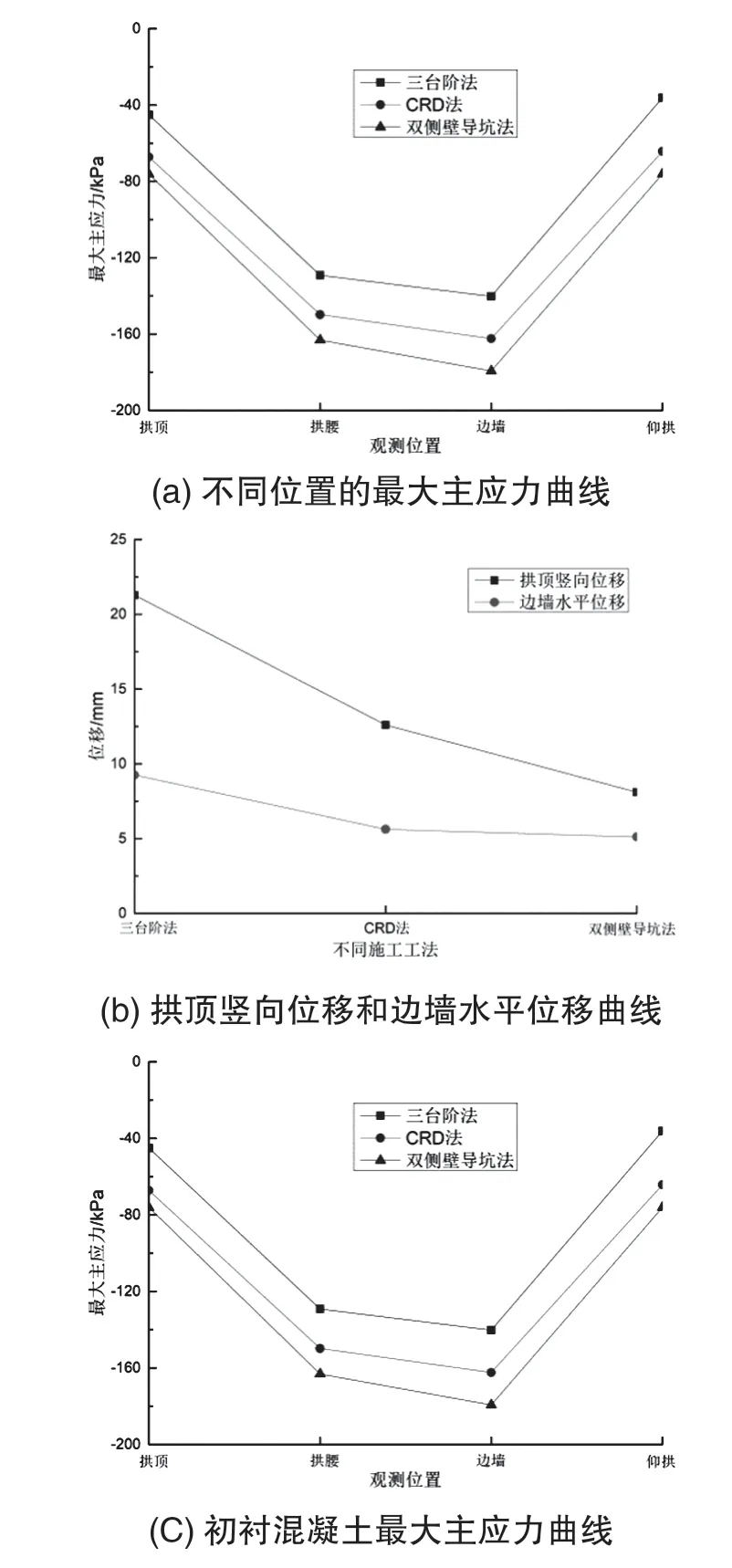
圖12 不同施工工法對比
4 結論
基于某淺埋暗挖公路隧道工程,利用有限元軟件建立隧道施工模型,分析三臺階法、CRD 法、雙側壁導坑法三種施工法下隧道圍巖和支護結構的受力變形情況,以獲得該工程最合理的施工工法。通過對比可知,采用雙側壁導坑法施工隧道時圍巖變形控制最佳,且受力狀態和穩定性最好,因此該工程最合理的施工工法為雙側壁導坑法。

