非線性時間分數階色散方程的分支問題與精確解研究

張 慧，芮偉國

(1.綿陽城市學院通識教育學院，四川 綿陽 621000；2.重慶師范大學數學科學學院，重慶 401331)

分數階導數的概念最早出現在1695年L’Hospital和Leibniz的往來書信中.此后，經過幾百年的發展，分數階微積分理論逐漸建立起來.與整數階微積分模型相比，越來越多的研究者發現分數階微分模型可以更準確地描述數學力學、控制理論、信號處理等各個領域的復雜問題.尤其在過去的幾十年間，分數階微積分被公認為是描述長記憶過程、黏彈性現象和反常擴散行為的最佳工具之一.

近幾十年來，出現了許多求解非線性分數階微分方程的有效方法.主要有Adomian分解法[1-2]、第一積分法[3]、同倫分析法[4-5]、李群論方法[6]、不變子空間法[7-8]、分數變分迭代法[9]、分數復變換法[10-11]、分離變量法[12-13]、分離變量法結合齊次平衡原理或積分分岔方法[14-15].這些方法對于求解更復雜的分數階非線性偏微分方程來說是遠遠不夠的.因此，尋找求解分數階非線性偏微分方程的新方法和新的分析工具成為當前和未來的首要任務.

本文利用文獻[16]關于分離變量法與動力系統方法相結合的思想，研究三階非線性時間分數階色散方程解的存在性、精確解和解的動力學性質.

1 三階非線性時間分數階色散方程Kα(0，2，0)

研究下列時間分數階色散方程[17]，記為Kα(m，n，p)：

(1)

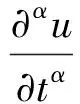
考慮三階時間分數階非線性方程Kα(0，2，0)：

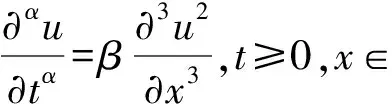
(2)

其中u=u(x，t)，α∈(0，1).當α=1時，文獻[18]深入研究了三階非線性色散方程的激波和爆破問題.文獻[19-20]首次在非線性色散方程Compacton解的觀點下研究了其一般情形.

方程(2)可化簡為

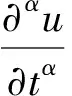
(3)

假設方程有如下形式的解：

u=[a0+a1v(x)]tγ.

(4)

其中：v=v(x)為待定函數；a0，a1，γ為待定常數.將(4)式代入(3)式得

(5)

利用齊次平衡原理，令γ-α=2γ，可得γ=-α.將γ=-α代入(5)式中，等式兩邊同時除以t-2α得

(6)

將(6)式對x積分一次，并令積分常數為零，則

(7)

(8)

當v=-a0/a1時，dy/dx無定義，由此稱v=-a0/a1為系統(8)的奇異線.顯然，當v=-a0/a1時，系統(8)與方程(7)不等價.為了使二者完全等價，只需做變換

dx=2βa1(a0+a1v)dτ，

(9)

其中τ為參數，則系統(8)可化簡為一個正則系統：

(10)

系統(10)與系統(8)具有相同的首次積分

(11)

其中h是積分常數.為了方便下面的討論，將(11)式改寫為

(12)

2 系統相圖分支

對系統(10)平衡點的性質及可能出現的相圖進行分析.除奇異直線v=-a0/a1外，系統(8)與系統(10)是拓撲等價的.因此，奇異系統(8)的相圖是由奇異直線v=-a0/a1周圍的拓撲結構和正則系統(10)的相圖構成.

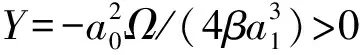
設M(v，y)，J(v，y)分別為系統(10)的雅克比矩陣和行列式，則有：

(13)

(14)

將平衡點代入(12)，(14)式中可得

(15)

(16)

根據平面動力系統的分岔理論[21-25]，有下面2個引理：

引理1 對于平面可積系統的平衡點有以下結論：(1) 當J(vi，yi)<0，系統的平衡點為鞍點；(2) 當J(vi，yi)>0且TraceM(vi，yi)=0，系統平衡點為中心；(3) 當J(vi，yi)>0且[TraceM(vi，yi)]2-4J(vi，yi)>0，系統平衡點為結點；(4) 當J(vi，yi)=0且Poincaré指數為0，系統平衡點為尖點，否則為高階奇點.

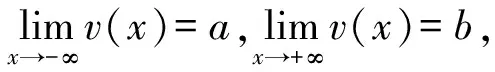
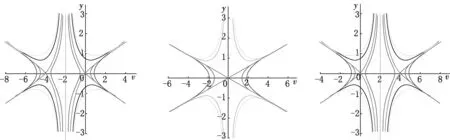
(1) 當a=b時，系統(8)具有同宿軌道，因此方程(7)具有孤立波形式的同宿解；

(2) 如果a≠b時，系統(8)有一條異宿軌道，因此方程(7)具有一個扭結或反扭結波形的異宿解；

(3) 若系統(8)有一條圍繞中心點的閉合軌道，則方程(7)具有周期解；

(4) 如果系統(8)具有等腰三角形的異宿軌道，且等腰三角形的底部是一條奇異線，則方程(7)具有尖波解.

由引理1易知：A點為尖點；C1，2點為鞍點；當βa1Ω>0時，B1，2點為鞍心，當βa1Ω<0時，B1，2點為中心.利用引理2可知，(7)式的孤立解對應于系統(8)的同宿軌道，方程(7)的異宿解對應于系統(8)的異宿軌道，方程(7)的周期解對應于系統(8)的閉軌道.

根據以上信息，在不同的參數條件下，繪制系統(8)的相圖分支，如圖1—2所示.需要注意的是，圖中的所有軌道曲線在平衡點外并不相交，一條軌道對應于方程(7)的一個解.

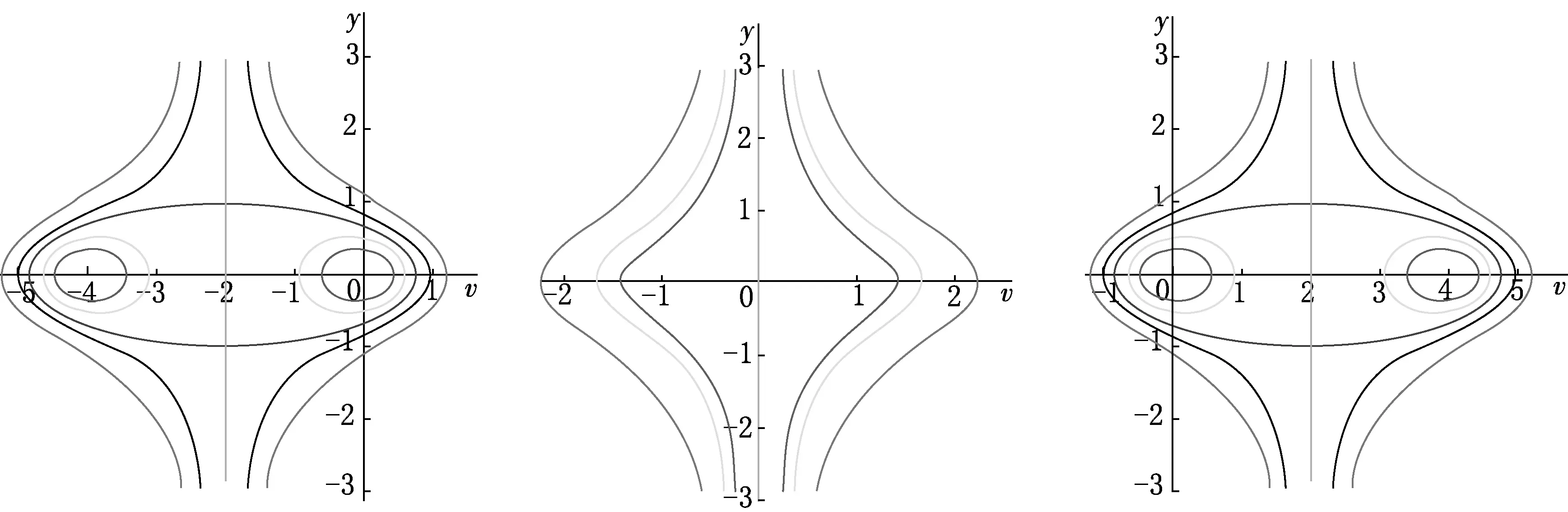
(a) a0>0 (b) a0=0 (c) a0<0

(a) a0>0 (b) a0=0 (c) a0<0

3 色散方程Kα(0，2，0)的精確解

系統(8)在不同參數下的相圖分支中的每一條軌道對應于方程(7)的一個解.

3.1 在h=h1，βa1Ω<0，a0≠0條件下色散方程Kα(0，2，0)的精確解

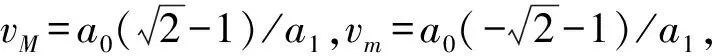
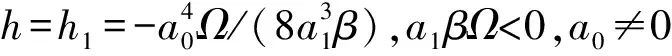
(17)

將(17)式代入系統(8)的第一個方程中，并沿通過點(vM，0)的閉軌道積分得

(18)

求解(18)式，可得(7)式的一個光滑周期解

(19)

(20)

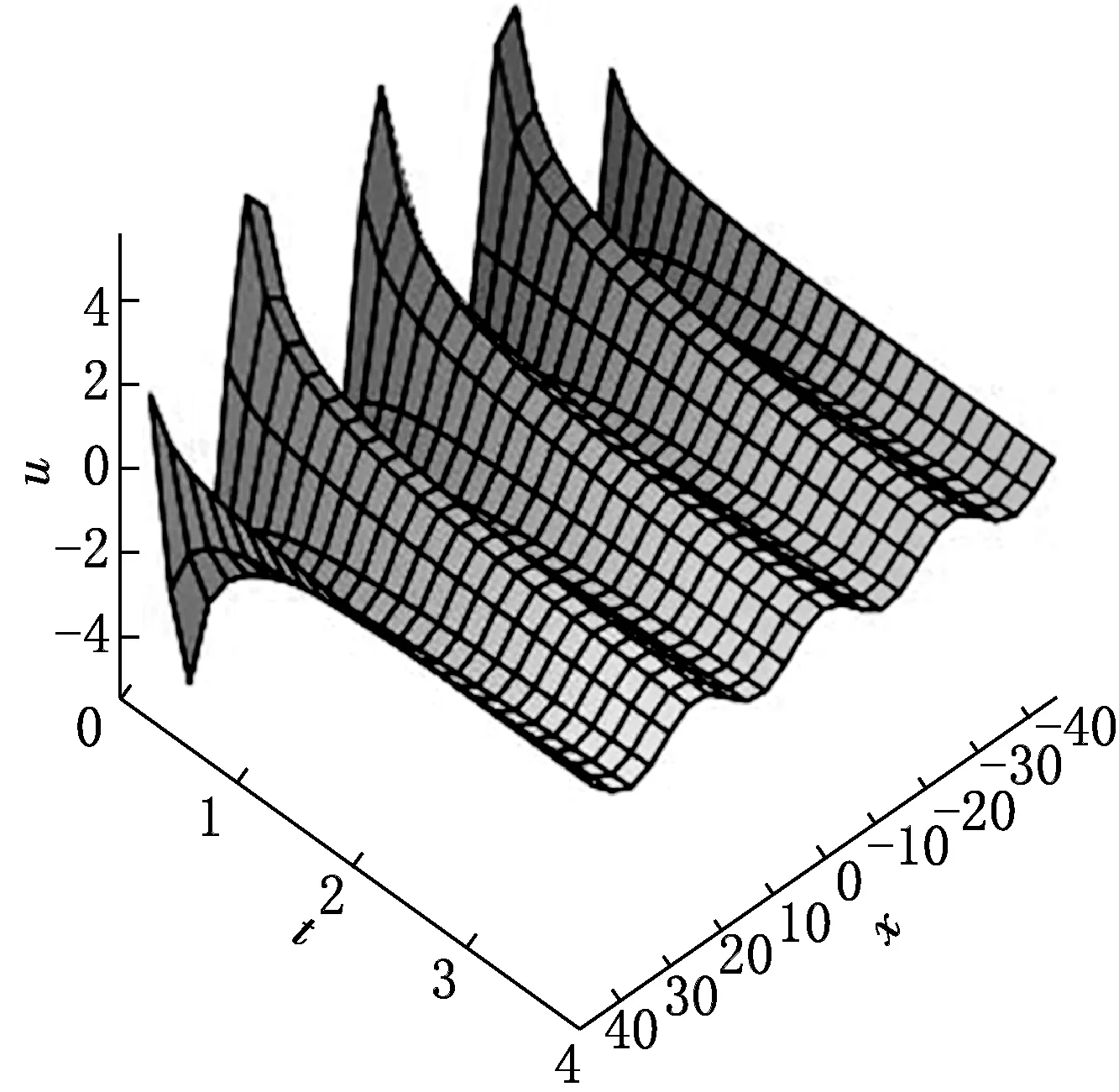
圖3 解(20)隨時間和空間變量演化的三維圖

由于當t→+∞時，u→0，故解(20)是具有周期性和衰減性的穩定解.為了直觀地顯示解(20)的動力學性質，取a0=a1=1，β=-2，α=0.75，繪制解(20)的動力學曲線圖，如圖3所示.

3.2 在h20條件下色散方程Kα(0，2，0)的精確解

當h20時，系統(8)圍繞中心點B1，2有無窮多個閉合軌道，圖1中可以看出，所有這些閉合軌道都有4個與v軸相交的點，由引理2 可知方程(7)具有無窮多個光滑的周期解.

在以上的條件下，方程(11)可化簡為

(21)

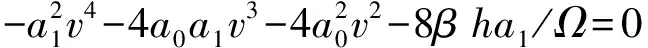
(22)

這里v1>v3>v4>v2.故(21)式可改寫為

(23)

以(v3，0)為初始條件，將(23)式代入(10)式的第一個方程，并積分可得

(24)

由此可得

(25)

其中

將(25)式代入變換(9)進行積分，可得

(26)

將(25)式代入(4)式，結合(26)式可獲得方程(3)的精確解：

(27)

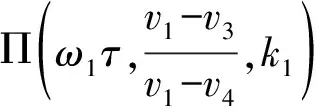
類似地，解(27)滿足當t→+∞時，u→0.故解(27)定義了一類具有周期性和衰減性的穩定解族，其動力學性質和剖面與解(20)非常相似.

3.3 在h>h1，β a1Ω<0，a0a1>0條件下色散方程Kα(0，2，0)的精確解

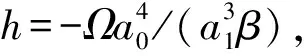
(28)

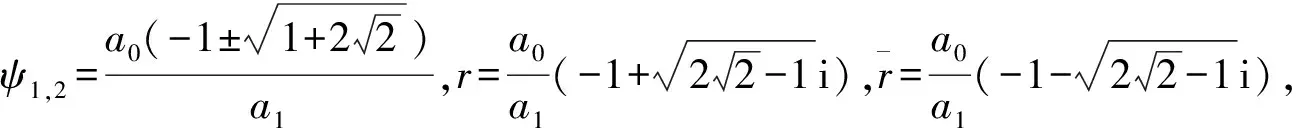
(29)

求解上式可得

(30)

其中：

將(30)式代入dx=2βa1(a0+a1v)dτ中，再積分，同樣令積分常數為0，可得

(31)

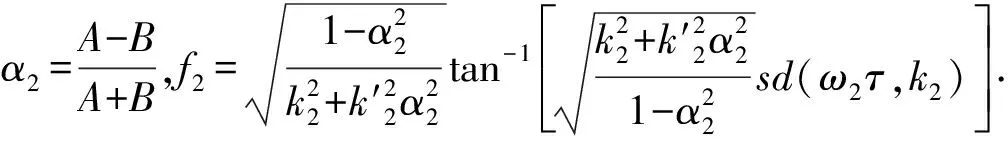
將(30)式代入(4)式，結合(31)式可獲得方程(3)的如下精確解：

(32)

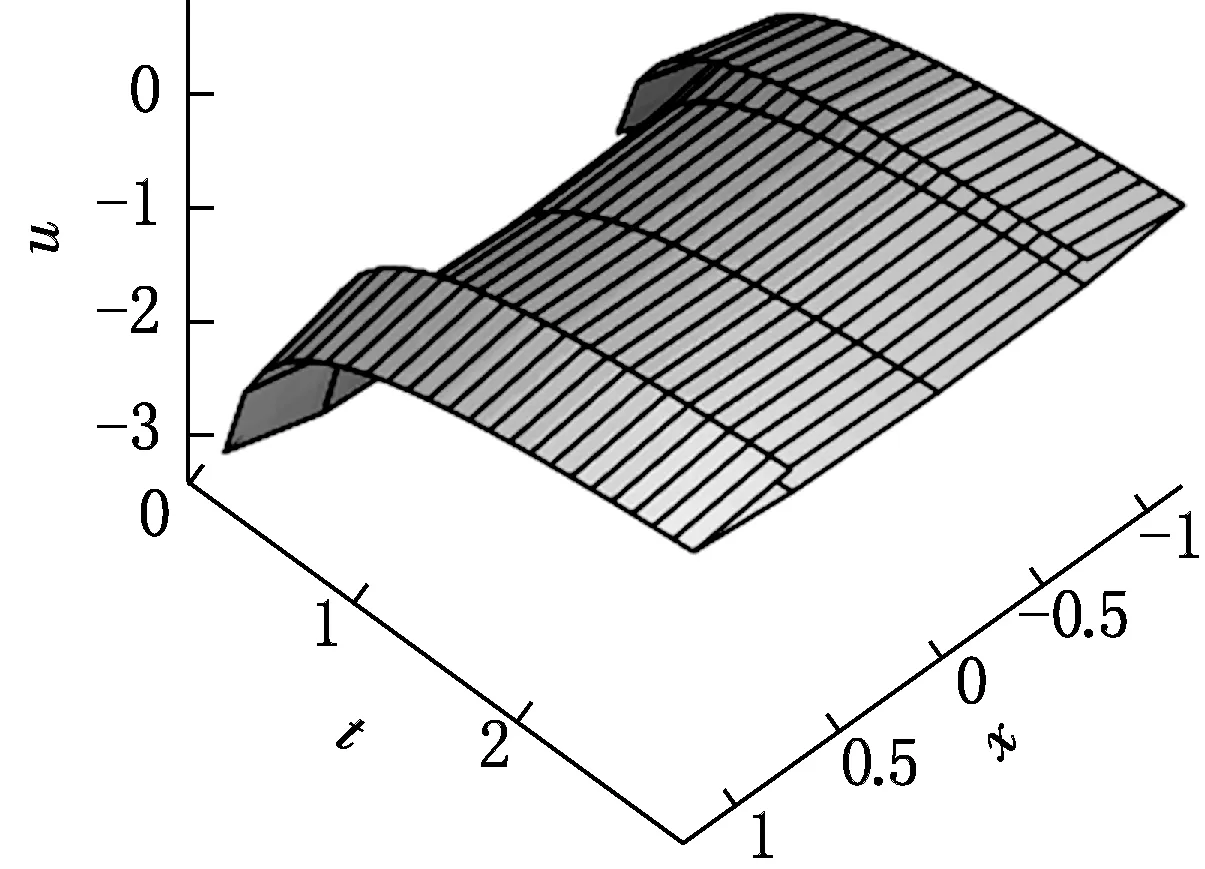
圖4 解(32)隨時間和空間變量演化的三維圖

當t→+∞時，u→0，故解(32)是一個具有Compaction性的漸進穩定解.為了直觀地顯示解(32)的動力學性質，取a0=a1=1，β=-2，α=0.35，繪制解(32)的動力學曲線圖，如圖4所示.

3.4 在h=h2，β a1Ω>0，a0>0條件下色散方程Kα(0，2，0)的精確解

當h=h2=0，βa1Ω>0，a0>0時，系統(8)總是有4條光滑的異宿軌道(見圖2)穿過鞍點B1(0，0)，B2(-2a0/a1，0).將上述條件代入(11)式，再將其代入(10)式中的第一個方程可得

(33)

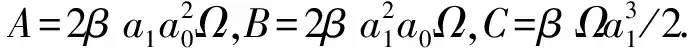
(34)

將(34)式代入dx=2βa1(a0+a1v)dτ中，再積分，同樣令積分常數為0，可得

(35)

將(34)式代入(4)式，再結合(35)式可獲得方程(3)的6個精確解：

(36)

(37)

(38)

(39)

(40)

(41)

其中:τ為參數，Ω=Γ(1-α)/Γ(1-2α)，α≠1/2.

為了能夠直觀地展示上述解的動力學行為，繪制一些具有代表性解的3維坐標演化圖形.取a0=a1=1，β=2，α=0.35，ε=1，繪制出解(36)的坐標演化圖形，如圖5(a)所示；取a0=a1=1，β=2，α=0.35，ε=-1，繪制出解(38)的坐標演化圖形，如圖5(b)所示.

(a)解(36)的3維圖 (b)解(38)的3維圖圖5 解(36)，(38)隨時間和空間變量演化的3維圖

3.5 在h10條件下色散方程Kα(0，2，0)的精確解

系統(8)在鞍點B1和B2兩側有無限多個弓形有界軌道，如圖2所示.根據引理2，對應于弓形有界軌道，(7)式有一簇緊性解.將h10代入方程(11)可得

(42)

同3.2節中方法一樣，(42)式可改寫為

(43)

以(v1，0)為初始條件，將(43)式代入(10)式的第一個方程，并積分得

(44)

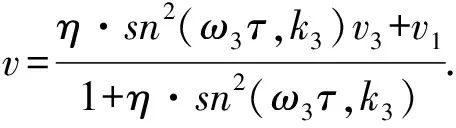
(45)

其中：

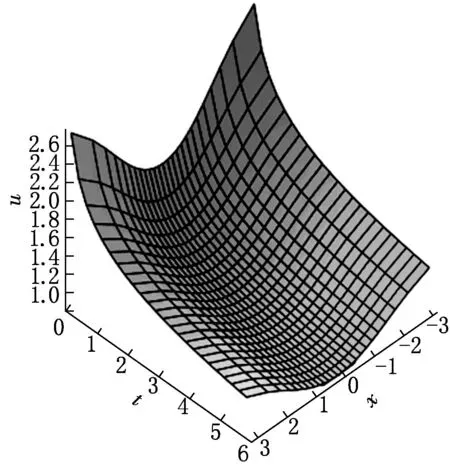
圖6 解(47)隨時間和空間變量演化的3維圖

將(45)式代入變換(9)進行積分，可得

(46)

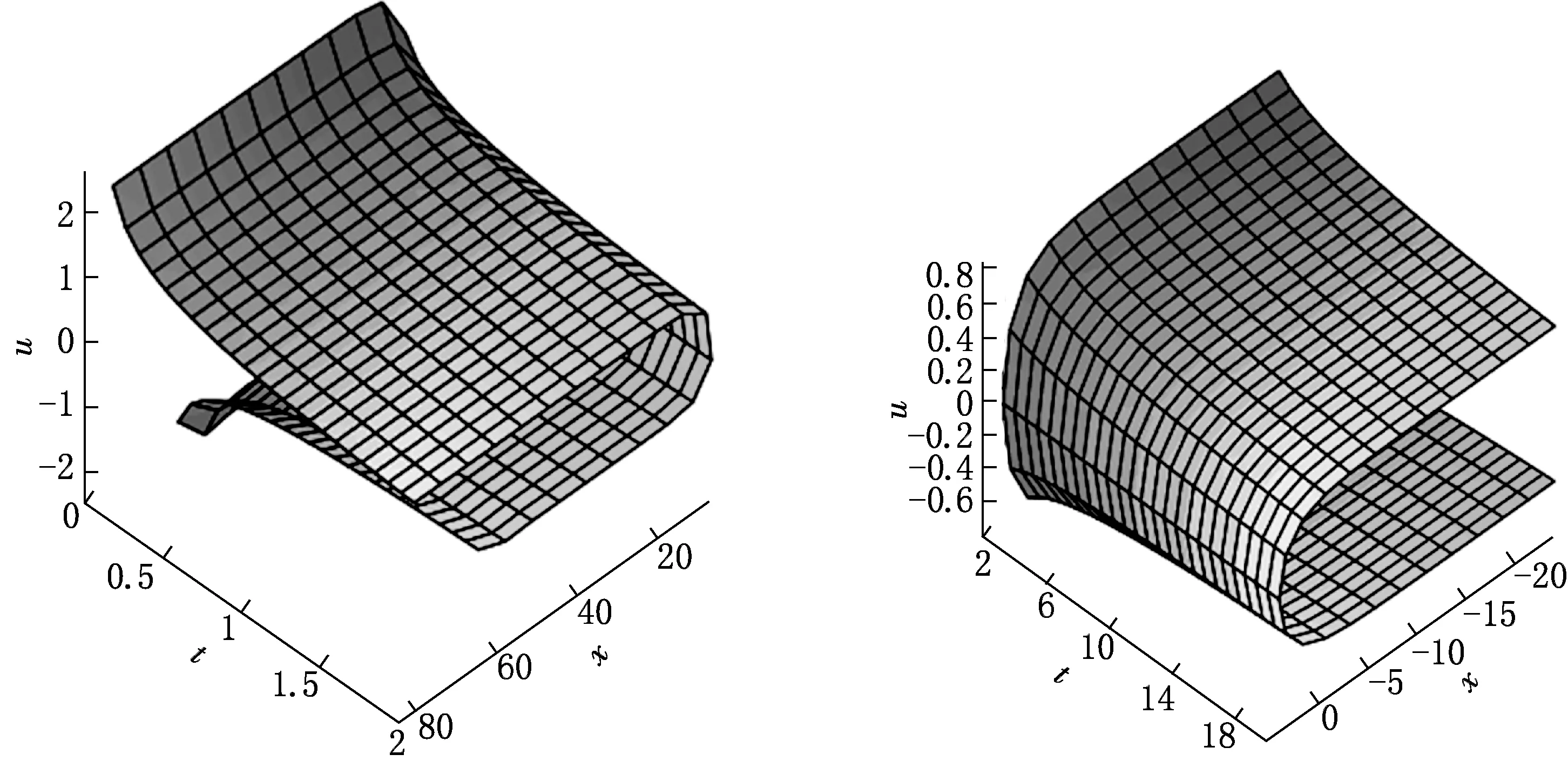
將(45)式代入(4)式，再結合(47)式可獲得方程(3)的一個精確解：

(47)

解(47)定義了一類具有compaction性的漸進穩定解.為了直觀地顯示解(47)的動力學性質，取參數a0=1，a1=0.5，β=2，α=0.25，t∈[0，6]，τ∈[-0.7，0.7]，繪制解(47)的動力學曲線，如圖6所示.

3.6 在h=h1，β a1Ω>0條件下色散方程Kα(0，2，0)的精確解

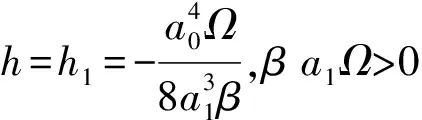
(48)

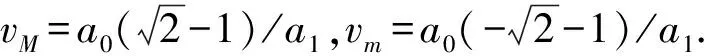
將(48)式代入系統(8)的第一個方程中，并沿通過點(vm，0)的閉軌道積分得

(49)

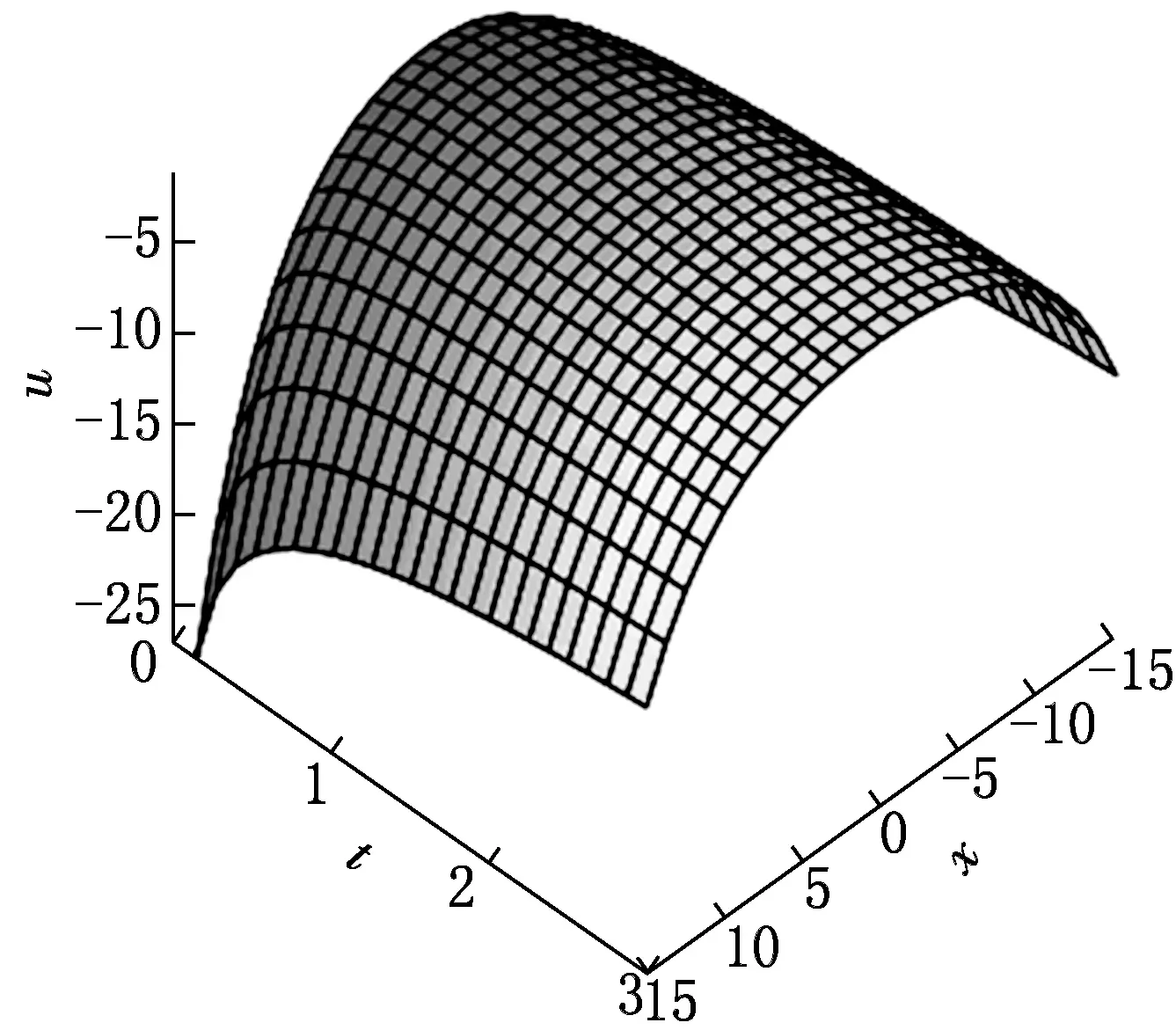
圖7 解(51)隨時間和空間變量演化的3維圖

求解(49)式，可得(7)式的一個無界解

(50)

(51)

當t→+∞時，u→0，故解(51)為無界漸進穩定解.為了直觀地顯示解(51)的動力學性質，取a0=a1=1，β=2，α=0.25，x∈[-15，15]，t∈[0，3]，繪制解(51)的動力學曲線圖，如圖7所示.

4 結論

本文利用分離變量法和動力系統法相結合的方法，研究了非線性時間分數階色散方程精確解的存在性問題及動力學性質.在一些特殊的參數條件下，得到了時間分數階色散方程不同類型的精確解，其中有些具有周期性，如解(20)、(27)，有些具有compaction性質，如解(32)、(47)，有些解具有無界特性，如解(51).它們大多具有隨時間增加而衰減的特性，滿足當t→+∞時，u→0.