基于樂隊花車效應的觀點動力學模型及其實證研究

徐涵,成思,沈浩

（1.華中科技大學新聞與信息傳播學院，武漢 430074；2.中國傳媒大學媒體融合與傳播國家重點實驗室，北京 100024）

1 引言

近年來，隨著互聯網與通信技術的高速發展，空間與時間對意見交換的限制被大幅削弱，跨時空對話、與素未謀面的陌生人交流變得輕而易舉，人們能夠更加便捷地分享自己的觀點、交流彼此的意見。個體之間進行觀點交互的社交網絡也因此變得愈發龐大復雜，各種不確定性因素隨之出現，使得輿論的演變充滿了不可控性，給輿情管理帶來了各種挑戰。

觀點動力學主要研究復雜網絡中的動態問題，其研究成果在輿情管理領域具有重要的實際應用價值，可以幫助應對新時代的輿情管理挑戰。在不同的觀點動力學模型中，考慮有界置信度的Hegselmann-Krause（HK）模型被廣泛應用于模擬各種真實情況，尤其是公眾意見演化。利用HK模型，我們可以模擬不同情況下的公眾意見演化過程，預測輿情事件發生后的輿論發展方向，為有關部門的輿情管理工作提供理論依據和技術支撐，輔助其制定輿情應對方案。

盡管自經典HK模型提出以來，許多學者已經對其進行了諸多改進研究［1-4］，但仍有許多會影響意見演變的因素尚未被納入模型的考慮范圍，比如在當今社會高頻出現的樂隊花車效應（Bandwagon Effect）的影響就仍未被考慮其中。因此，為了使觀點動力學模型更加符合輿論演化的實際情況、基于模型產出的輿情應對方案更具有價值，本研究基于樂隊花車效應對經典HK模型進行擴展，提出了一種新的基于樂隊花車效應的觀點動力學模型（Bandwagon Effect-Based Hegselmann-Krause Model，BEHK模型），并通過仿真實驗進行了實證研究，驗證新模型的有效性。

2 相關研究

在觀點動力學的發展過程中，最初，研究者們提出了很多經典模型來研究觀點演化過程。這些經典模型可以按照觀點值的類型被分為離散觀點演化模型和連續觀點演化模型兩大類。其中，經典的離散觀點演化模型有投票者模型（Voter Model）［5］、多數裁定模型（Majority-vote Model）［6］和勸導者模型（Sznajd Model）［7］等；連續觀點演化模型主要有談判者模型（Deffuant Model）［8］和 HK 模型［9］。

由于離散觀點演化模型認為個體的觀點是“非黑即白”的，而在大部分輿情事件中，個體的觀點往往不會如此絕對，因此本研究選擇認為個體觀點值可以在一定區間內連續變化的連續觀點演化模型作為研究的基礎模型。而在經典的連續觀點演化模型中，談判者模型認為個體在更新意見時僅和與其觀點相近的一個個體相互作用，HK模型則認為個體會與鄰居中所有觀點相近的個體進行相互作用。考慮到當今社會的輿情事件多發于互聯網，個體往往處于一對多的狀態，因此本研究選取更貼合情況的HK模型作為具體的基礎模型進行改進研究。

在經典的HK模型中，個體只與那些意見在其置信范圍內的鄰居進行交流，并在意見更新時將這些人的平均意見作為自己的新意見；如果沒有鄰居，個體意見將保持不變。給定一個社交網絡G=(V,E)，其表達式如式（1）所示。

其中Oj(t)表示個體j在t時刻的意見；Ni(t)表示t時刻可以與個體i交換意見的鄰居集合，其范圍如式（2）所示，(2)中εi代表個體i的置信范圍。

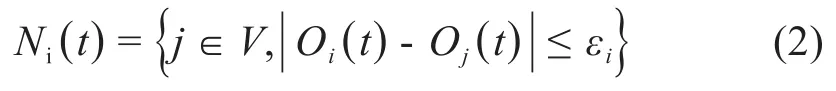
目前，許多研究者致力于通過引入新的影響意見演化的因素來對經典HK模型進行改進。在信任因素的影響方面，Fu等［10］認為現實世界中個體對自己和鄰居意見的信任程度存在差異，當個體更新意見時，獨立考慮自己的意見會更合理，基于此提出了修正的HK模型（MHK模型），其表達式如（3）所示。

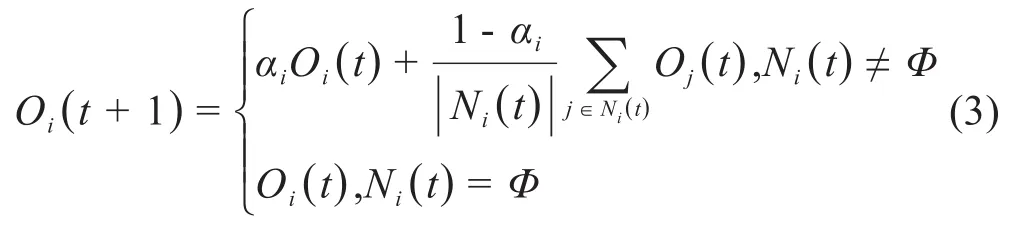
其中αi∈［0,1］代表個體對自己觀點的信任程度，鄰居集合Ni(t)的范圍在經典HK模型的基礎上剔除了個體自己。張亞楠等人［11］考慮到人與人相互交往過程中存在心理關系上親疏程度的差異，引入參數關系度，提出了一種新的關系HK模型。蘇炯銘等人［12］發現連續觀點動力學模型中缺乏對個體信任及其觀點的不同權重的考慮，引入個體間的信任度和觀點間的相似度兩個參數，基于HK模型，將有限信任假設擴展為有限影響假設，建立了帶權重的觀點更新模型。回顧相關文獻，可以發現已有研究涉及較多的是個體與個體間的內部信任對觀點演變的影響。

而所謂樂隊花車效應［13］，來源于心理學的概念，指的是一種行為模式在群體中的加速擴散，一個人做某件事的概率隨著已經這么做了的人的比例增加而增加。當它應用于觀點動力學領域時，指個體對多數意見會持更信任的態度，個體在群體的引導或施加的壓力之下會懷疑并改變自己的觀點，使其與群體中大多數人的意見保持一致。也就是說，在個體之間進行意見交互從而更新觀點的過程中，當個體意見與群體意見相差大時，個體會更信任群體意見，個體對意見的信任程度受到意見與群體意見差異的影響。Wang等［14］用閾值模型對集體把關中的人際效應和樂隊花車效應進行建模，發現集體把關人中的樂隊花車效應是在線新聞傳播的主要驅動力，為理解集體把關對信息傳播的影響做出貢獻。楊超［15］基于兩個真實案例分析了突發事件傳播中的樂隊花車效應，并從政府、意見領袖和大眾三個層面對此提出了解決建議。

基于樂隊花車效應，本研究提出在經典HK模型中引入群體意見因素，并提出在意見更新過程中，將個體對其鄰居意見的信任系數建模為當前時刻個體自身意見與群體意見之差的函數關系。與現有的研究相比，本文的創新點在于考慮到了網絡中個體對外部群體環境的信任及個體意見與群體意見的差異對個體意見信任程度的影響，從而能夠更好的對社交網絡上的觀點演化進行建模。

3 模型結構

本研究將網絡中的個體分為普通個體及意見領袖個體，所有個體的初始意見值在［-1,1］隨機分布。給定一個社交網絡G=(V,E)，這些個體在意見演化過程中遵守以下規則：

①群體意見受所有個體意見影響，它可以是當前時刻所有個體意見的均值。用Xc(t）表示t時刻的群體意見，則其表達式為式（4）：

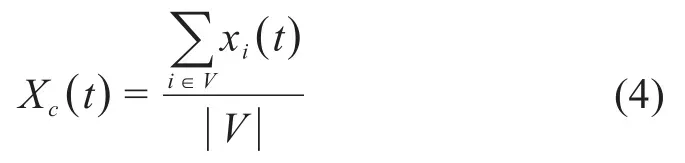
其中xi(t)代表個體i在t時刻的意見值。

②個體中存在一種固執個體，其意見值始終等于初始值。

③非固執普通個體只會接觸置信范圍內的普通鄰居，但會接觸置信范圍外的意見領袖。在意見更新時，其意見受上一時刻自己的意見、普通鄰居的意見、相鄰意見領袖的意見和群體意見的影響，表達式如式（5）所示。

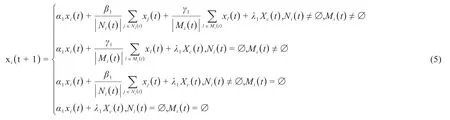
其中Ni(t)代表t時刻與個體i相鄰且在置信范圍內的普通個體集合，Mi(t)代表t時刻與個體i相鄰的意見領袖個體集合，α1、β1、γ1、λ1分別代表個體對自己的意見、普通鄰居的意見、意見領袖的意見、群體意見的信任程度，α1+β1+γ1+λ1=1。

基于樂隊花車效應，個體對多數意見會持較信任的態度，所以當個體意見與群體意見相差大時，個體會更信任群體意見，即λ1大，α1小；當個體意見與群體意見無差異時，個體對自身意見與群體意見的信任程度持平，即α1=λ1，可以用公式（6）表示這種關系。

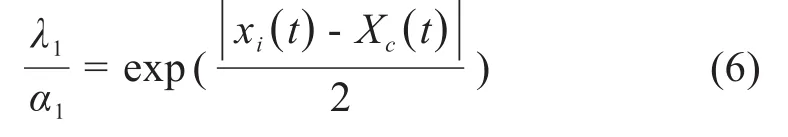
④在意見更新時，非固執意見領袖個體的意見受上一時刻自己的意見、相鄰意見領袖意見、群體意見影響，表達式如式（7）所示。

其中Nk(t)代表t時刻與意見領袖個體k相鄰的意見領袖個體集合，α2、β2、λ2分別代表意見領袖個體對自己的意見、其他意見領袖的意見、群體意見的信任程度，α2+β2+λ2=1。與（6）類似，α2與λ2的關系如（8）所示。

非固執普通個體在進行意見更新時，可能的個體連接情況和對應公式初始權重分配如下所示：

①非固執普通個體的意見受到自己的意見、普通鄰居的意見、相鄰意見領袖的意見和群體意見的影響，則可能的初始系數為：

α11=0.2,β11=0.1,γ11=0.4,λ11=0.3

②如果非固執普通個體沒有在置信范圍內的普通鄰居，則其意見只受自己的意見、相鄰意見領袖的意見和群體意見的影響。可能的初始系數為：

α12=0.2,β12=0,γ12=0.5,λ12=0.3

③如果非固執普通個體沒有與之相連的意見領袖，則其意見只受自己的意見、普通鄰居的意見和群體意見的影響。可能的初始系數為：

α13=0.2,β13=0.5,γ13=0,λ13=0.3

④如果非固執普通個體沒有在置信范圍內的普通鄰居和與之相連的意見領袖，則其意見只受自己的意見和群體意見的影響。可能的初始系數為：

α14=0.4,β14=0,γ14=0,λ14=0.6

以上是初始權重分配的一種可能情況。這樣設置的原因是：由于樂隊花車效應的存在，λ1＞α1更有可能出現；同時由于這是初始階段，個體對群體意見的感知并不明顯，所以仍然可能存在大于λ1的權重。

非固執意見領袖個體在進行意見更新時，可能的個體連接情況和對應公式初始權重分配如下所示：

①非固執意見領袖個體的意見受到自己的意見、相鄰意見領袖的意見和群體意見的影響，則可能的初始系數為：

α21=0.3,β21=0.3,λ21=0.4

②如果非固執意見領袖個體沒有相鄰意見領袖，則其意見只受自己的意見、群體意見的影響。可能的初始系數為：

α22=0.4,β22=0,λ22=0.6

初始權重分配這樣設置的原因與前文相同。

4 實證研究和結果分析

4.1 實驗設置

數據集：為了驗證BEHK模型的有效性，我們在兩個人工生成網絡（BA無標度網絡和WS小世界網絡）和兩個真實物理世界網絡（ego-Facebook網絡和feather-lastfm-social網絡）中進行了觀點演化實驗。其中BA網絡和WS網絡系通過相關網絡生成算法生成，ego-Facebook網絡和feather-sastfm-social網絡獲取自斯坦福網絡分析平臺。ego-Facebook網絡數據集由Facebook的朋友列表組成，數據來源于使用Facebook APP的調查參與者；feather-lastfm-social網絡是來自亞洲國家的LastFM用戶的社交關系，于2020年3月從公共API中搜集。這4個網絡的基本特征如表1所示：

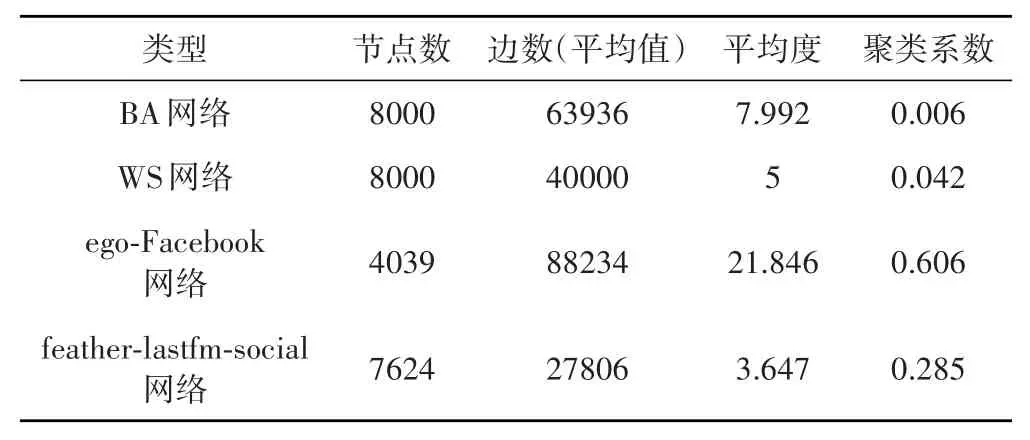
表1 四種復雜網絡的基本特征

實驗參數：仿真實驗中使用的參數如下：

-意見領袖比例：θ=2%、θ=10%

-個體置信度：ε=0.2、ε=0.6、ε=0.9

-初始狀態下個體對群體意見的信任系數：λ=0.1、λ=0.01、λ如第3部分所示

-在群體意見計算公式中，意見領袖意見與普通個體意見的權重比：η=1、η=3、η=10

4.2 BA網絡實驗結果

在有8000個節點的BA網絡中進行模擬實驗，為意見領袖比例θ和個體置信度ε賦不同的值，觀點演化結果如圖1所示。從圖1整體可以看出，考慮樂隊花車效應，在群體觀點和意見領袖的共同影響下，無論θ和ε如何變化，除固執個體外，其他個體的觀點都能在較短時間內達成共識。當θ=0.02和ε=0.2時，我們可以看到，固執個體在整個過程中都保持初始意見不變，而其他非固執個體在第11天的時候以極小的意見區間達成共識。當ε值從0.2增加到0.6，非固執個體在第9天達成共識，且共識意見區間增大。當ε值增加到0.9時，非固執個體在第7天達成共識，達成共識所需的時間進一步減少，共識意見區間進一步增大。

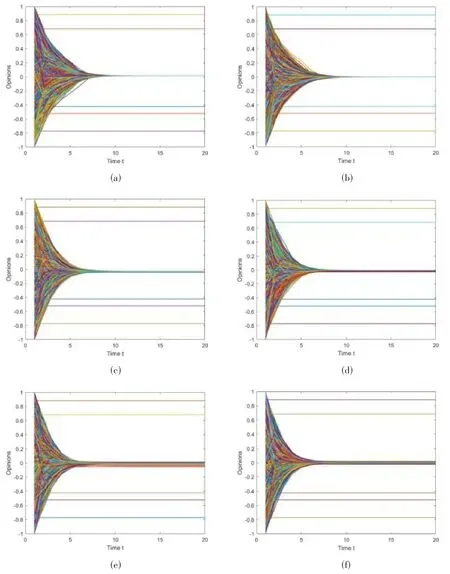
圖1 不同意見領袖比例和個體置信度對BA網絡中觀點演化的影響。

4.3 WS網絡實驗結果

在有8000個節點的WS網絡中進行仿真實驗，為個體置信度ε和個體對群體觀點的初始信任系數λ賦不同的值，意見演化結果如圖2所示。與BA網絡中的仿真結果相似，非固執個體可以在較短時間內達成共識。θ=10%時，ε值從0.6降至0.2，非固執個體達成共識所需的時間變長，最終的共識意見區間變窄。當θ=10%和ε=0.6時，圖2(a)、(c）和（d）分別為λ如第3部分所示、λ=0.1和λ=0.01時的仿真結果。我們可以看到λ越小，初始階段的觀點變化越慢。當λ小到一定程度時，就會出現“折角”現象。這是因為在初始階段，當群體觀點的影響力降低時，個體就會更多地考慮自己和鄰居的意見，他們的自信水平會相應提高，觀點的變化幅度會減小。

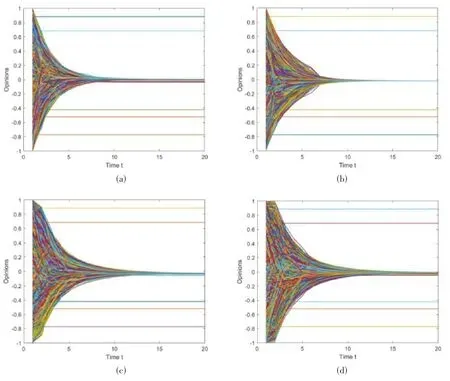
圖2 不同個體置信度和個體對群體意見的初始信任系數對WS網絡中觀點演化的影響。

4.4. ego-FaceBook網絡實驗結果

在有4039個節點的真實ego-FaceBook網絡中進行同樣的仿真實驗，意見演化結果如圖3所示。與BA網絡和WS網絡中的實驗結果相似，給定不同的θ和ε值，非固執個體可以在較短時間內達成共識，且達成共識所需的時間和最終共識觀點區間與ε值有關，此結果不受網絡規模的影響。

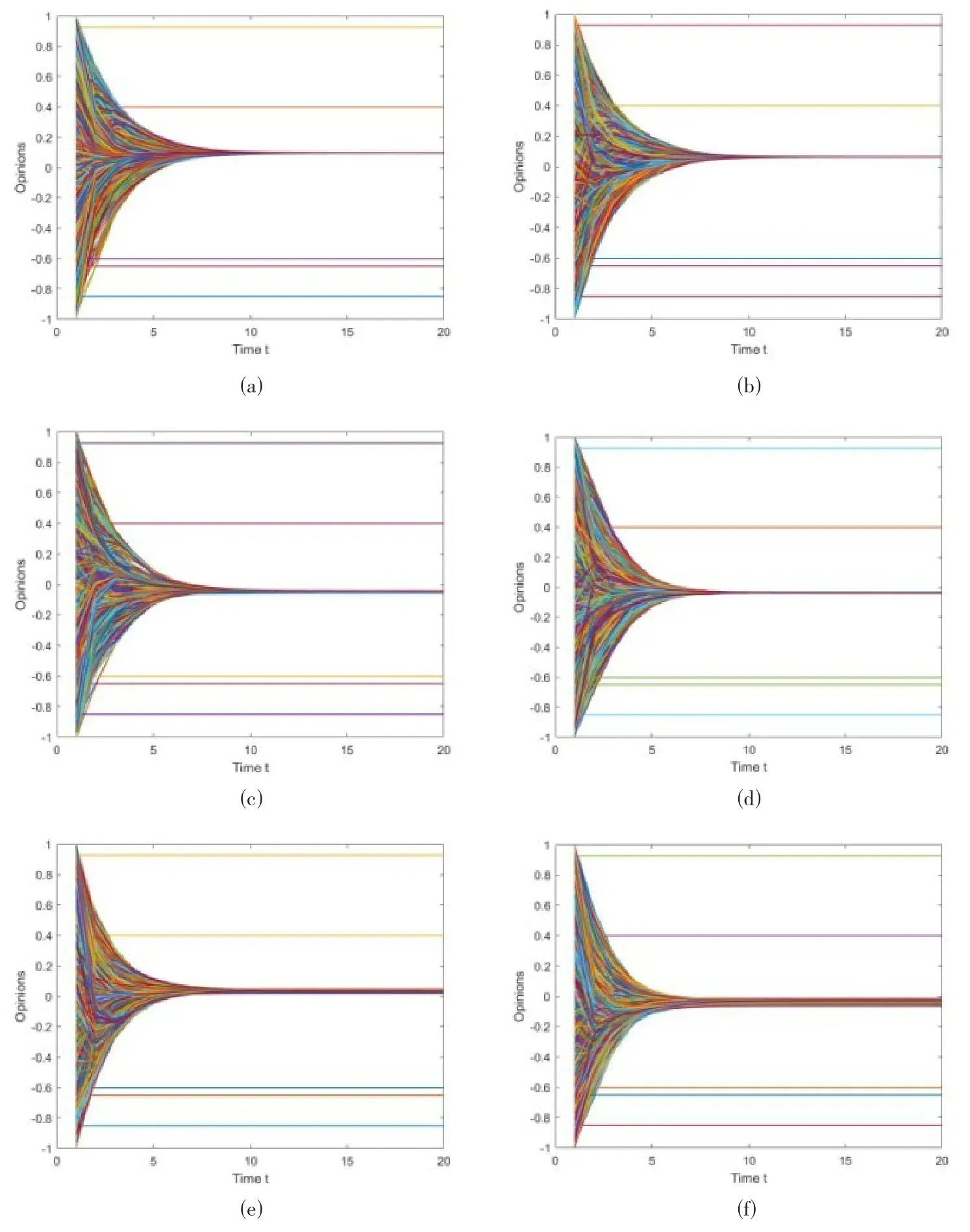
圖3 不同意見領袖比例和個體置信度對ego-FB網絡中觀點演化的影響。

4.5 Feather-lastfm-social網絡實驗結果

為個體置信度ε賦不同的值，并在群體觀點更新計算公式中調整意見領袖的意見權重，在有7624個節點的真實feather-lastfm-social網絡中進行相同的仿真實驗，觀點演化結果如圖4所示。對比圖4(a）和（b）可以看出，與上述三種網絡的仿真結果相似，幾乎所有的非固執個體都能在較短時間內達成共識。θ=2%時，ε從0.6減小到0.2使非固執個體達成共識需要的時間增加，最終共識觀點區間變窄。但與上述情況不同的是，在這個真實網絡中，有大量個體位于網絡邊緣。因此，在觀點演化的過程中，由于缺乏意見的交換，會有極少數的個體被隨機孤立。在圖4(a）和（b）中，我們可以看到每個圖中都有一個孤立個體，他們的最終觀點與群體觀點不一致。圖4(a)、(c)、(d）分別為η=1、η=3、η=10時的模擬結果。我們可以看出，在群體觀點更新計算公式中，意見領袖觀點與普通個體觀點的權重比例不會影響最終達成共識的結果，但共識觀點區間大小是隨機的。

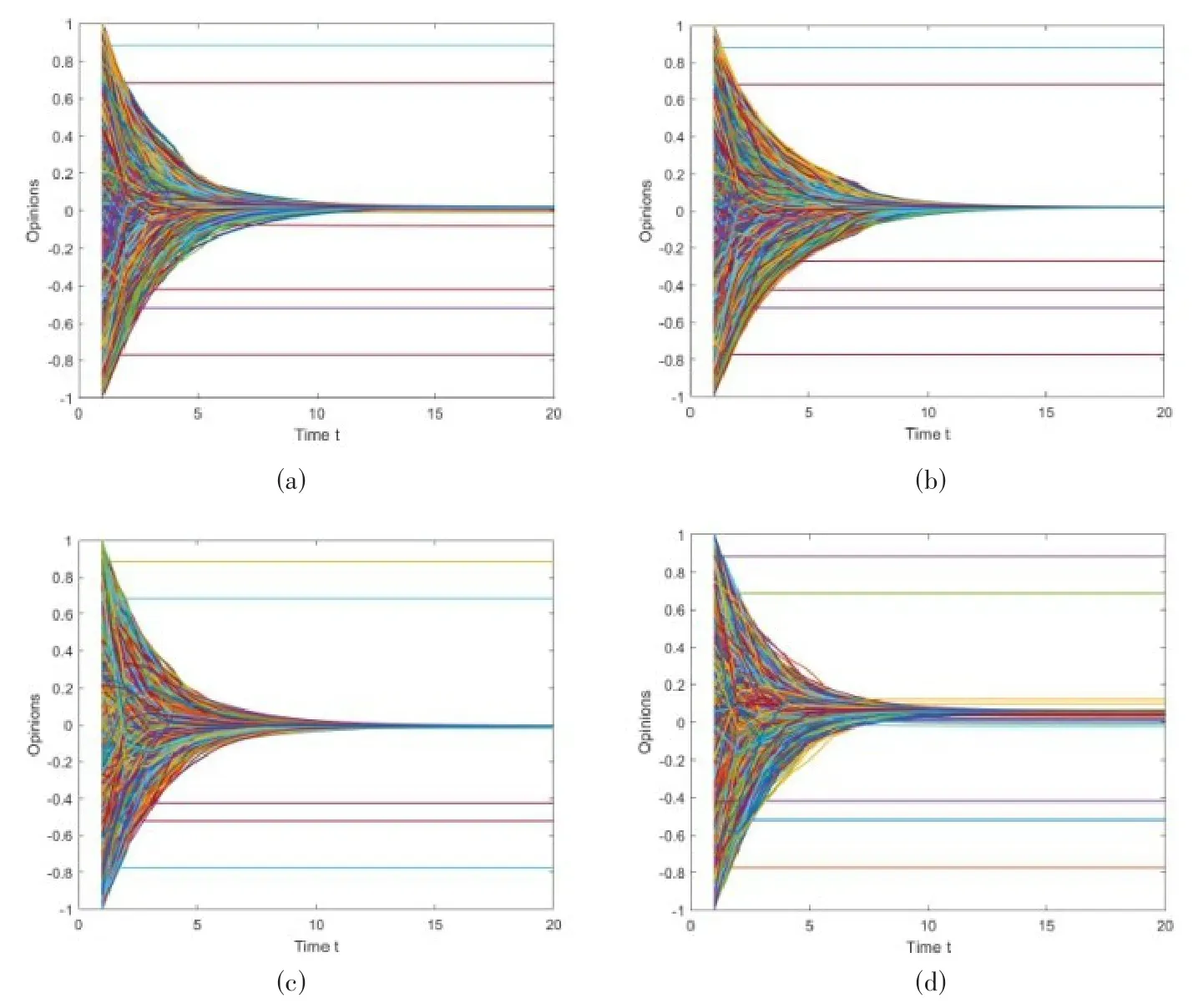
圖4 不同個體置信度和群體觀點更新公式中意見領袖觀點權重對feather-lastfm-social網絡中意見演化的影響。

5 結語

本研究基于樂隊花車效應，考慮群體觀點和信任程度等因素，提出了一種新的基于樂隊花車效應的Hegselmann-Krause觀點動力學模型。實證分析結果表明，考慮樂隊花車效應，在群體觀點和意見領袖的共同影響下，無論θ和ε如何變化、網絡規模如何，除固執個體和孤立個體外，其他個體的意見都能在較短時間內達成一致。個體置信度越小，達成共識所需的時間越長，最終的共識區間范圍越窄。此外，個體對群體意見的信任程度也會影響意見變化幅度。在初始階段，個體對群體意見的信任系數越低，意見變化幅度越小。

本研究已經在兩個人工生成的網絡數據集和兩個真實的網絡數據集上得到了廣泛的實驗結果，但后期還可以在規模更大的真實社交網絡數據集中進行實驗，以進一步驗證所提出模型的有效性與魯棒性；此外，在大量的實驗中，我們發現除部分固執個體和孤立個體外，群體中的最大觀點值會隨著時間的推移而嚴格降低，而群體中的最小意見值會隨著時間的推移而嚴格增加，因此群體意見在有限的時間內會不可避免地趨于一致。在今后的工作中，如何嚴格證明模型的收斂性以及明確收斂時間下界，值得進一步研究。