評析2021年高考數學中的結構不良問題
蔣靜霞



【摘 要】 與常規的結構良好問題相比,高考試題中的結構不良問題以其開放性,給考生充分的選擇空間,能充分考查學生對數學知識的理解和運用的能力.此類題型科學把握了數學題型與數學思維的開放性,在高考改革中兼顧了平穩過渡和創新.本文通過研究2021年高考中的結構不良問題,探討其在數學核心素養培養中的重要作用,并試談在新高考背景下高中數學教學如何引入此類題型的策略.
【關鍵詞】 結構不良;學科素養;教學啟示
在2019年由教育部考試中心制定的《中國高考評價體系》中,正式發布了以“一核”、“四層”、“四翼”為主要內容的高考評價體系,落實立德樹人的根本任務,發揮高考的引導作用,體現高考的育人功能[1].在《普通高中數學課程標準》(2017年版2020年修訂)中,提出數學素養是現代社會每一個人應該具備的基本素養,數學教育與考試評價承載著立德樹人和發展素質教育的功能[2].2021年的數學科高考命題在課程標準與高考評價體系的指引下,命題以數學核心素養的落實為導向,創新運用了多種新題型,結構不良問題是其中重要的一類.
1 結構不良問題的內涵
結構良好問題是初始狀態、目標狀態和算子都很明確的問題,而結構不良問題則是這三者中至少有一個沒有明確界定的問題[3].所謂算子,就是解決問題的方法和途徑.學生在平常的學習和考試中常見的試題一般都是結構良好的試題,條件不多不少,學生只要在掌握了知識與方法的前提下,充分利用題目給出的條件就能解答既定的問題.然而現實生活中所遇到的問題多是結構不良型,能順利地解決結構良好問題并不能保證可以成功地解決現實生活中的結構不良問題.因此,結構不良問題的出現能從一個新的角度考查學生的素養和能力,在日常教學中能促進學生核心素養和能力的養成,在考試中能發揮選拔的功能.
2 例舉結構不良問題在2021年高考數學中的應用
在2021年的高考中,數學科高考積極貫徹《深化新時代教育評價改革總體方案》,加大了題型的開放性與創新力度,多份試題出現了結構不良問題,利用結構不良問題考查考生的數學學科核心素養和關鍵能力,能讓素養和能力突出的考生在考試中脫穎而出,讓只會刷題、思維定勢的考生在考試中自亂陣腳,發揮出高考試題的選拔性.下面對此類題型中的全國卷甲卷的18題和乙卷的16題,以及新高考二卷的14題、22題進行評析.
2.1 目標明確,條件開放的結構不良問題
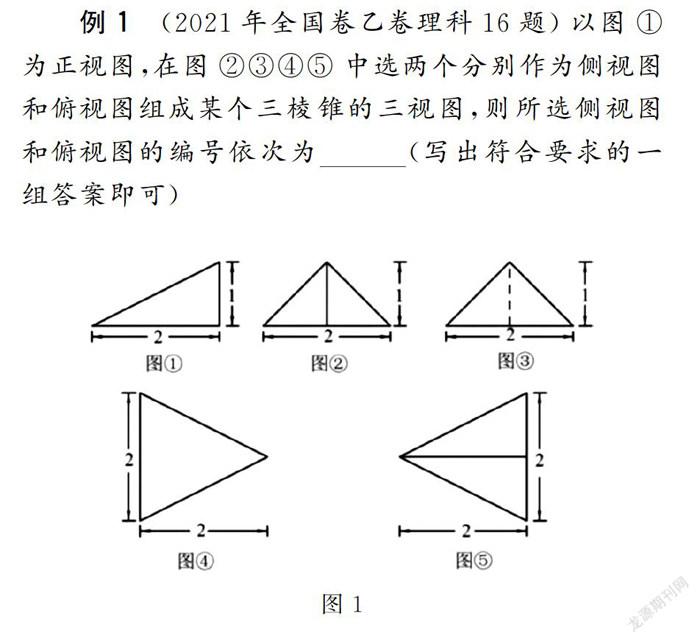
例1 (2021年全國卷乙卷理科16題)以圖①為正視圖,在圖②③④⑤中選兩個分別作為側視圖和俯視圖組成某個三棱錐的三視圖,則所選側視圖和俯視圖的編號依次為(寫出符合要求的一組答案即可)
命題立意分析 本題以結構不良型為載體、直觀想象的數學核心素養為導向考查考生的直空間想象能力.本題需要考生根據給出的三棱錐的正視圖,結合余下的視圖,選出合適的側視圖和俯視圖還原幾何體.試題的答案不唯一,而正確的答案只有兩個.考生需要會觀察視圖并想象原幾何體,著重觀察的視圖不同,答案也不同.考查了考生的空間想象能力,能夠拉開差距,體現高考的選撥功能.
解析 由正視圖的高度可知,側視圖只能是②或③,分析和觀察題目給出的5個視圖,可以嘗試在長方體中還原幾何體.當側視圖是②的時候,俯視圖是⑤,如圖2;當側視圖是③的時候,俯視圖是④,如圖3.所以答案是②⑤或③④.
3 結構不良問題在數學核心素養培養中的重要作用
2021年是中國新高考評價體系頒布后實施新高考的第二年,新高考引領新的數學教學方法,落實核心素養.結構不良問題的再度開放,對在教學中數學核心素養的培養中有著重要作用.
3.1 引領教學回歸教材、注重核心素養培養
少數教師在新授課教學中和備課復習中片面理解高效課堂,為了趕教學進度,不僅自己不用教材,而且不引導學生用教材,視教材知識為無物,往往只花很少的時間探究新知識,而把大量的時間花在總結題型解法訓練上,只重結果,忽視了知識的生成與發展,更談不上對學生數學閱讀與理解能力的培養.新高考新題型結構不良問題的出現,讓這種教學方式的缺點在高考中暴露無疑,同時也讓習慣于只會被動接收知識且只會條件反射解常規題型的考生無所適從.啟示教師不能舍本逐末,忽視基礎知識的教學,忽視學科素養培養的真正落實.
3.2 與“雙減”政策相呼應、摒棄題海戰術
結構不良問題的出現會對只靠機械盲目刷常規題型的學生造成一定的沖擊.在教學中,應整體布局和設計,科學、準確把握習題的容量、難度,防止“題海戰術”,避免盲目刷題.新授課的習題應注重梯度、由淺入深,幫助學生掌握基礎知識、基本技能的同時獲得數學經驗的積累和數學思維的逐步提升;思考題應關注情境和問題的創設,幫助學生理解數學本質,提升數學核心素養;復習題應關注主線之間的關聯,構建知識網路,與六個數學核心素養相協調.
3.3 重思想重能力、體現育人功能
2021年數學科高考中結構不良試題的命制,使學生體會到,在數學的學習中不能僅僅只會解答結構良好的數學問題,也要關注如何解決現實生活中所遇到的結構不良問題,引導學生從單純地接受知識轉向問題的解決、策略的選擇,體現數學的育人功能.
4 高中數學課堂在新高考背景下引入結構不良問題的策略
為了發揮結構不良問題在落實核心素養培養中的重要作用,在新高考新教材的背景下,要恰當、適時地在日常教學中引入結構不良問題.如何引入?下面筆者將從新知探究、課堂練習、復習鞏固三個方面進行探討.
4.1 新知探究——在數學實驗探究中引入結構不良問題
高考數學中結構不良試題的引入,積極和深刻地考查了學生的數學理解能力、數學探究能力,而在缺乏探究的機械式的教學中很難培養學生的創新思維.這就要求教師能夠針對教學中的某個內容,精心設計能引發學生積極探索的教學過程,使學生在體驗數學研究的過程中培養學習掌握、實踐探索、思維方法的學科素養.
例如 以北師大版必修二的三視圖的教學為例.不少學生對立體幾何的章節知識都是望而生畏的,原因是空間想象能力欠缺,歸根結底是缺乏直觀想象的數學核心素養.在本章節中,教師應多開展實驗探究,借助多媒體,利用好幾何畫板等數學軟件,化抽象為具體.在三視圖這一節,筆者設計這樣一道結構不良的題目:
在以下四個幾何體中,有相同的三視圖的兩個幾何體是?? .
學生通過觀察作出四個幾何體的三視圖,發現圖4和圖7的三視圖相同,圖5和圖6的三視圖相同.而教師則利用幾何畫板展示四個幾何體由正方體切割得到的過程,進一步補充“補形”的方法.
4.2 課堂練習——在變式中結合結構不良問題
在平常教授新課中,課本練習是評價教師的教與學生的學達成程度的必不可少的一個環節.而教材中的例題多為結構良好的問題,教師可以將課本的例題變式,通過改變條件或問題,或者整合幾個題目,改編為結構不良的問題.
例如 以北師大版必修四第三章第三節《二倍角的三角函數》的例題為例.課本中的例2為:設α是第二象限角,已知cosα=-35 ,求sin2α,cos2α,tan2α的值.
通過改變條件和簡化問題,變成目標明確、條件開放的結構不良問題如下:
變式練習 從下面兩個條件中選擇一個,求sin2α的值
①tanα=43,5π4<ɑ<3π2;
②sin ɑ+cos ɑ= 45;
③sin(ɑ+π4)=35 .
可以發現,同樣是求二倍角的正弦函數值,選擇的條件不同,難度也不同,但是都是考查三角恒等變換的問題.在通過變式成開放性的結構不良問題的過程中,由淺入深的變化中加強了數學運算的素養的培養.
4.3 復習鞏固——在構建知識網絡中引出結構不良問題
例如 以函數的復習為例.為解決本文中的例3(2021年高考全國新Ⅱ卷14題)類型的問題,考生需要熟練掌握所學過的函數類型及相關性質,若只是片段教學,沒有及時進行歸納總結和與相關的其他章節的知識串聯形成知識網絡,則需要花較多的時間去回想所學過的基本初等函數類型并與題目的條件對照,才能得到正確的答案.
在復習課中形成知識網絡的重要方法是利用好思維導圖.若平時注重花時間繪制適合自己的思維導圖,將高中所學過的基本初等函數的定義、圖像、運算性質、函數性質等歸納起來,本題將很快迎刃而解.
參考文獻:
[1]教育部考試中心.中國高考評價體系.北京:人民教育出版社,2019
[2]中華人民共和國教育部.普通高中數學課程標準(2017年版2020年修訂). 北京:人民教育出版社,2020
[3]李同吉,吳慶麟.論解決結構不良問題的能力及其培養[J].華東師范大學教育科學學報,2006(1):63-68.

