“垂直平分線”和“角平分線”的應用
阮秋月


【摘要】“垂直平分線”和“角平分線”是學習初中數學和解決數學問題中常遇和常用的“兩線”,它們在定義、性質和判定等方面具有一些相通點.本文嘗試在分析這些相同點的基礎上,尋找用“兩線”解決問題的巧妙之處,從而幫助初中生更高效的解題.
【關鍵詞】“垂直平分線”;“角平分線”;數學解題
“垂直平分線”和“角平分線”作為初中數學幾何部分的內容,在代數部分也舉足輕重,尤其是在壓軸題中其綜合性體現得非常明顯.同時,“兩線”結合也是學生解題的難點所在,如何巧妙應用“兩線”解決數學問題,對提升學生的解題效率和準確率非常關鍵.
1 “垂直平分線”和“角平分線”的相通之處
“垂直平分線”和“角平分線”雖然是初中幾何部分兩個不同的教學內容,但是它們的知識點安排,如定義、性質、判定、尺規作圖等,具有異曲同工之妙.教師要想學生能夠靈活、巧妙的利用“垂直平分線”和“角平分線”解決數學問題,就要讓學生對這“兩線”各自的內容及其相通之處有所了解[1].本文認為,“垂直平分線”和“角平分線”的相通之處主要體現在以下四個方面:
首先,定義相通.從“垂直平分線”和“角平分線”這“兩線”的定義不難看出,“垂直平分線”重在說明線段被平分,而“角平分線”重在說明角被平分.所以,從“垂直平分線”和“角平分線”這“兩線”在定義方面的相通之處在于“平分”,即抓住了“平分”也就抓住了從“垂直平分線”和“角平分線”這“兩線”的定義.
其次,性質相通.從“垂直平分線”和“角平分線”這“兩線”的性質可以看到,“垂直平分線”和“角平分線”這“兩線”都重在說明“距離相等”,這是它們的相通之處.不同的是,“垂直平分線”中的“距離”是指點到點的距離,而“角平分線”中的“距離”是指點到邊的距離.總之,抓住“距離相等”和“點到點的距離”、“點到邊的距離”幾個關鍵詞,就可以掌握“垂直平分線”和“角平分線”的重點和難點.
再次,判定相通.“垂直平分線”和“角平分線”的判定都是證明一條線的屬性或歸屬.如“垂直平分線”的判定定理證明的是一條直線是一條線段的垂直平分線,“角平分線”的判定定理證明的是一條射線是一個角的平分線.但需要注意它們的不同,那就是證明一條直線為垂直平分線時,需要分別證明兩個不同的點在這條直線上,而證明一條射線為角平分線時,需要說明這個點在這個角的內部[2].由此可見,抓住了它們的不同之處,也就抓住了它們的本質.
最后,作法相通.從“垂直平分線”和“角平分線”的尺規作圖方法不難看出,“垂直平分線”的尺規作圖方法是“角平分線”的尺規作圖方法的基礎,都要以兩個不同的端點為圓心,都要以大于線段二分之一的長度為半徑,都是兩條圓弧的交點.換言之,“角平分線”的尺規作圖是在“垂直平分線”的尺規作圖基礎上進行的[3].另外,作法相通還表現在圖形的構造上,都凸顯了全等三角形和等腰三角形.第一,在作“垂直平分線”時,圓弧的交點和線段端點、垂直平分線就構造出了兩個全等的三角形,在這作“角平分線”時,兩種不同圓弧的交點與角平分線就構成了兩個全等三角形.第二,線段兩個端點和一個圓弧交點形成的圖形為等腰三角形;畫角平分線的理論依據就是等腰三角形的“三線合一”,即底邊的垂直平分線和頂角的角平分線“合二為一”,這里再一次說明了“垂直平分線”的尺規作圖方法是“角平分線”的尺規作圖方法的基礎.
2 基于“兩線”的初中數學題巧解思路
2.1 利用“平分”巧解
例1
如圖1所示,在△ABC中,∠ACB=90°,BE平分∠ABC,交AC于點E,DE垂直平分AB于點D.
求證:BE+DE=AC.
點撥與解析本題是典型的“垂直平分線”和“角平分線”結合問題.由于BE、DE和AC很難發現他們之間的數量關系,但是可以通過轉化的方法將這三條線段化為一條,這就是數學中典型的化歸思想.具體可以按如下步驟操作:首先需要借助“垂直平分線”的性質將BE和AE相互轉換,然后要利用“角平分線”的性質將CE和DE相互轉換.在轉換之后,便容易由AC=AE+EC得到AC=BE+DE.
2.2 利用“距離相等”巧解
例2
如圖2所示,已知∠AOB 平分線上一點E,且EC⊥OA,ED⊥OB,垂足分別為點 C,D.
求證:(1)OC=OD;(2)OE是CD的垂直平分線.
點撥與解析 本題中兩次利用到了“距離相等”,第一次是利用了角平分線中的“點到邊距離相等”,即DE=EC,第二次是利用了垂直平分線的“點到點距離相等”,即OD=OC,這是“垂直平分線”和“角平分線”中典型的“距離相等”相通之處.看到“∠AOB 平分線上一點E,且EC⊥OA,ED⊥OB”,馬上就要想到是角平分線的性質,看到“OC=OD”,馬上就要想到是否與線段的垂直平分線有關,這都是靈活解題的表現.而“垂直平分線”和“角平分線”還有“全等三角形”相通之處,所以(1)(2)兩問是否可以借助這一相通之處解決就變得非常重要.
2.3 利用“全等”巧解
例3
如圖3所示,在△ABC中,DF是邊BC的垂直平分線,AD是△BAC一個外角的角平分線,DF與AD相交于點D,DE⊥于 E,且 AB > AC.
求證:BE-AC=AE.
點撥與解析 本題是要證明BE、AC、AE三邊之間的關系,而從圖形中不難發現AB-BE=AE.很明顯,這需要構造三角形并證明它們全等,恰巧“垂直平分線”和“角平分線”有一個相通之處是“作法相通”,根據上文分析其實就是“三角形全等”.基于此,就應該馬上想到如何利用“垂直平分線”和“角平分線”構造出“全等三角形”,而這就需要連接DB和DC,同時還需要過D點作DM⊥AC.這樣作輔助線的靈感主要來自三個方面:其一,連接DB和DC是由“DF是邊BC的垂直平分線”這個條件想到;其二,過D點作DM⊥AC是由“AD是△BAC一個外角的角平分線”這個條件想到;其三,構造“全等三角形”是由“BE-AC=AE”這個條件想到.
2.4 利用“相等”巧作輔助線
例4
已知,如圖4所示,點B、C在∠A的兩邊上,且AB=AC,P為∠A內一點,PB=PC,PE⊥AC,PF⊥AB,垂足分別為E、F.
求證:PE=PF.
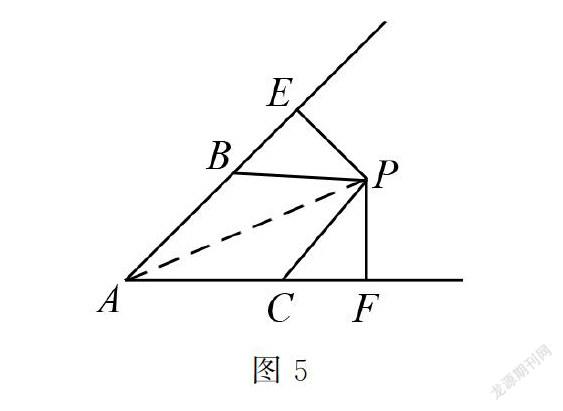
點撥與解析 本題是非常典型的“兩線”問題.在“兩線”問題中,往往需要依靠作輔助線才能得到解決,而如何作輔助線,其中有一定技巧,抓準題中“相等”關系的量非常關鍵,如本題中的“AB=AC”、“PB=PC”,都是巧作輔助線的突破口.所以,本題的解決思路大體是:首先,如圖5所示連接AP.然后,根據
AB=AC、PB=PC,外加一條公共邊AP,就證明了△ABP和△ACP是全等三角形,在此基礎上得到∠BAP=∠CAP.再結合P為∠A內一點,得到AP為∠A的角平分線.最后,根據PE⊥AC,PF⊥AB,結合角平分線的性質可知PE=PF.需注意的是,首先,本題中證明AP是∠A的角平分線不能僅憑∠BAP=∠CAP這一個條件得到,而需結合P為∠A內一點這個條件,因為“角平分線的判定”中明確了“在角的內部”這一基礎條件,切勿遺漏.其次,本題中綜合了角平分線的性質和判定,而這學生對這兩大內容極易混淆,在本題解決過程中切勿因混淆而致錯.
3 “兩線”問題解決過程中應避免的錯誤
在初中數學幾何部分,“垂直平分線”和“角平分線”是非常重要且基礎的兩個知識點,其一方面體現在知識體系規善上,另一方面體現在解題思維拓展上.但是,無論從哪個方面審視該知識點,都應注意以下易錯點的規避:
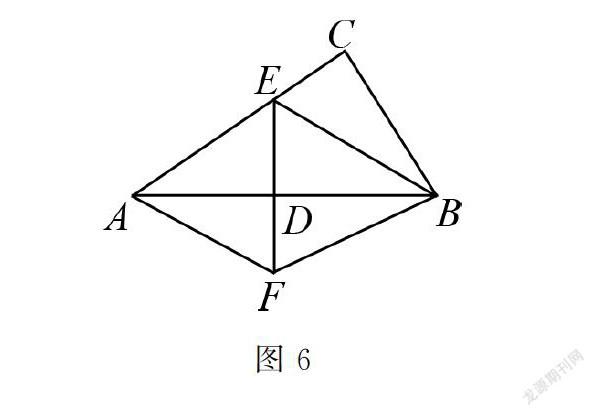
第一 準確理解“平分”.相對而言,角平分線中的“平分”比較容易理解,無論是在其性質還是判定都是如此.這里所說的準確理解“平分”,重點在于垂直平分線.如圖6所示,由于DE垂直平分AB,易得DE⊥AB和AD=DB,這是正確的解題思路.但是,很多同學容易在類似于圖6的問題中出錯,認為在DE垂直平分AB的情況下還可以得到ED=FD.
第二 準確區分性質與判定.無論是垂直平分線,還是角平分線,它們都有性質與判定.
首先,垂直平分線的性質是“線段垂直平分線上的點與這條線段兩個端點的距離相等”,垂直平分線的判定是“到一條線段兩個端點距離相等的點,在這條線段的垂直平分線上.即線段垂直平分線可以看成到線段兩端點距離相等的點的集合”.不難看到,垂直平分線的性質和定理是互逆的,要想精準掌握,還需仔細揣摩.這里需注意的是,在判定垂直平分線時,需證明兩個點同時在一條直線上才能得到該直線為垂直平分線上,這是學生極易犯錯之處.如圖6所示,只依靠AE=BE,DE垂直AB只能證明點E在直線EF上,還應用同樣的方法證明點F也在直線EF上,然后才能得到直線EF是線段AB的垂直平分線.另外需注意的是垂直平分線是直線,而角平分線是射線,這是它們的本質屬性.
其次,角平分線的性質是“角平分線上的點到角兩邊的距離相等”,角平分線的判定是“角的內部到角的兩邊距離相等的點,都在這個角的平分線上”.這里需要注意的是,“角平分線的判定”中明確了“角的內部”這一基礎條件,證明時切勿遺漏該條件.正如例4中,在證明AP是∠A的角平分線時,一定要結合“∠BAP=∠CAP”和“P為∠A內一點”兩個條件.要知道,在例4中明確給出了“P為∠A內一點”,學生在解本題時要意識到這一條件絕對不是命題者“多此一舉”.
參考文獻:
[1] 劉頓.兩線聯姻,輕松解題[J].初中生之友,2011(29):32-33.
[2] 王友峰.“三用”線段垂直平分線和角平分線定理解題[J].初中生學習指導:初三版, 2012(17):103-105.
[3] 趙興榮,祁樂珍.線段垂直平分線與角平分線的“證”與“用”[J].數學學習與研究, 2011(20):86-86.

