直線共軛液壓泵齒輪齒廓嚙合參數的幾何分析*
朱學明,許 蘢
(江蘇聯合職業技術學院,江蘇 鹽城 224005)
0 引 言
直線共軛內嚙合齒輪泵由于結構緊湊、流量脈動小、噪聲低等顯著優點在高端機床、塑料機械、海洋裝備、航空航天等領域有廣泛應用[1]。率先成功研發第一臺直線共軛內嚙合齒輪泵的是瑞士Turninger公司[2],此項設計技術仍由國外掌握,目前還沒有公開完整規范設計體系。
國內大多學者以單一公式法、仿真法研究了直線共軛齒輪泵,而忽略其幾何意義。當直線共軛齒輪某些參數超過范圍時,純公式計算將會出現嚴重錯誤;同時單一公式計算并不能動態反映動態直線共軛齒輪嚙合過程。由于缺乏理論的指導,國內通過仿制法獲得的產品仍與發達國家產品有較大差距,研究思路并未獲得較大進展,魏偉鋒等[3]通過研究指出構建高效嚙合幾何模型的重要性;徐學忠等[4]研究了直線共軛齒輪,通過向量方程求解速度最終獲得滑動系數,過程較為繁瑣,同時僅獲得單一滑動系數;董永昌等[5]、徐學忠等[6]學者研究了其部分嚙合特性,但都缺乏嚙合參數的系統分析;許蘢等[7]雖然基于Willis定理建立幾何模型分析了重合度、嚙合線以及共軛線,顯示幾何分析的巨大威力,但并未對嚙合角、壓力角、滑動系數嚙合參數進行進一步分析和計算。
幾何對嚙合角、壓力角、滑動系數等分析有著先天的優勢,若超過范圍將無法作圖,同時可動態進行分析與計算,因此對其的研究顯得非常有必要。專為它開發分析軟件并不經濟,結合常用的SolidWorks軟件、Excel軟件就可對直線共軛齒輪嚙合的整個過程進行動態分析,從而指導設計。
諸多資料在研究直線共軛內嚙合泵時都采用了一些范例,由于這些范例具有通用性,筆者同樣以范例形式進行幾何分析和計算。重點是通過使用幾何方法對直線共軛齒輪的嚙合參數進行分析,得出齒廓嚙合的規律,為直線共軛齒輪齒廓設計提供參考。
1 工具及基本理論
齒輪設計應考慮各嚙合參數如嚙合角、壓力角、滑動系數等,目前已有資料中的齒輪嚙合參數求解都圍繞嚙合線方程展開。直線共軛齒輪傳動是一個動態過程,也是嚴格的幾何嚙合過程,同樣可通過幾何方法進行求解。
1.1 求解工具介紹
SolidWorks是優秀CAD/CAM軟件之一,它具有功能強大、易學易用和技術創新的特點,使用它可使設計更加高效。
與本文相關為參數化草圖功能,草圖中常用的幾何關系:水平()、豎直()、垂直(),剪切可自動產生交點()等;一旦標注尺寸,默認為驅動尺寸,也可修改為從動尺寸;參數化草圖中數據導入Excel軟件后可根據需求設定間隔后進行進一步分析和求解,同時保持幾何關系。
1.2 直線齒廓基圓及嚙合線概念
直線共軛齒輪組其中一個齒輪齒廓為直線,由于直線特殊性,過圓心O1點作直線齒廓反向延長線的垂線,垂足為F,將以O1F為半徑的圓稱為直線齒廓齒輪基圓,在傳動過程中基圓不發生改變,如圖1所示。
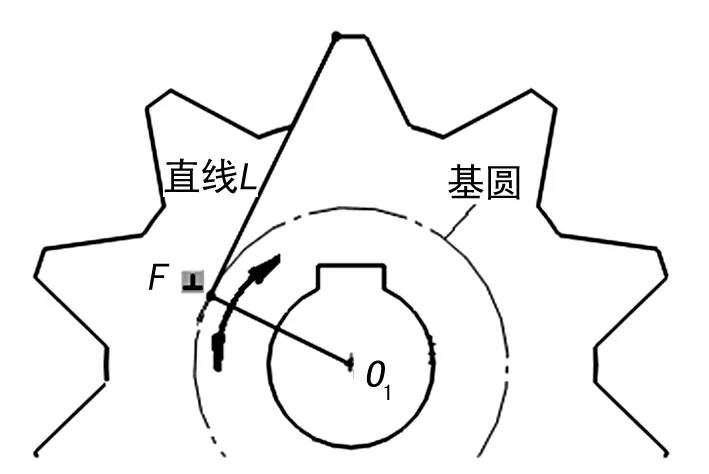
圖1 直線齒廓齒輪基圓定義
根據Willis定理[8],過兩節圓交點P點作齒輪1直線齒廓所在直線L的垂線,垂足為E點,rj1為節圓1的半徑(定值驅動尺寸),O1F為定值(驅動尺寸),拖動直線L(O1F繞著O1旋轉,并且保持O1F⊥EF),可獲得嚙合點E的軌跡即為嚙合線,則PE為公法線,直線L(EF)為公切線,如圖2所示。
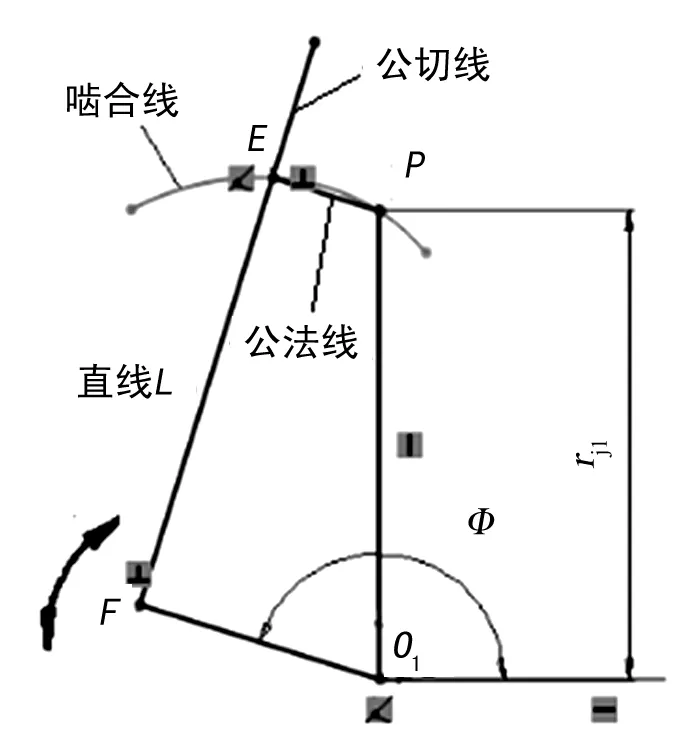
圖2 嚙合線生成
1.3 嚙合角定義
嚙合線與兩節圓公切線所夾銳角稱為嚙合角(漸開線齒輪定義)。嚙合角較小時,重合度較高,齒面滑動系數較大,齒根較瘦,抗彎強度較差,不適合大扭矩傳遞,反之相反[8]。
對于直線共軛齒輪,根據定義E點為嚙合線上的一點,作兩節圓的公切線,則角θ為嚙合角,嚙合角隨著E點的移動而變化。如圖3所示,嚙合角θ它是一個變化值,和漸開線齒輪嚙合角為固定值不同。
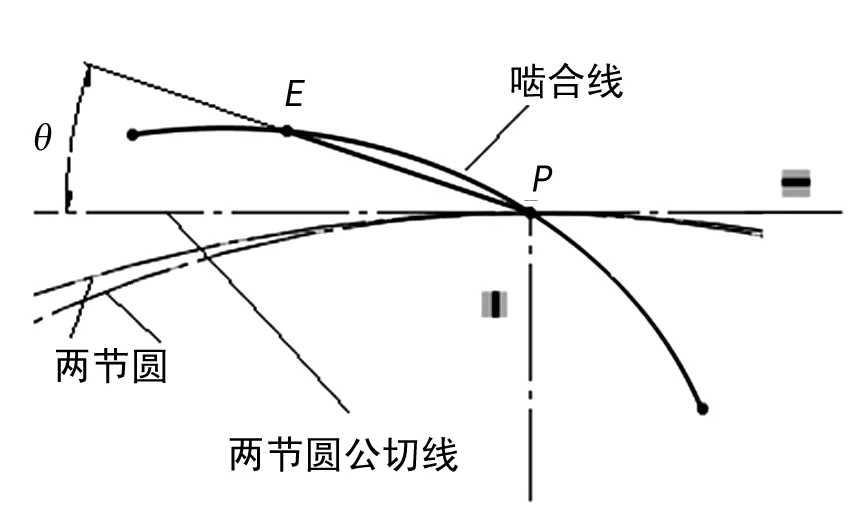
圖3 嚙合角幾何定義
1.4 壓力角定義
力方向與其作用點速度方向所夾的銳角稱為壓力角,即該作用點法線方向與速度方向夾角[8]。壓力角越小,傳動性能好;壓力角越大,實際有用功越小,它只增加了摩擦力矩。機構運動中壓力角不斷變化,一般機構壓力角不超過50°。
對于直線共軛齒輪,E點為嚙合線上一動點,切線為EF,法線為PE。過E點作EZ垂直于O1E,EZ為速度的方向,如圖4所示,角α即為齒輪1壓力角,它是一個變化值,同理可幾何作圖求出齒輪2的壓力角。

圖4 齒輪1壓力角幾何定義
1.5 滑動系數定義
齒輪嚙合點處兩齒間相對切向速度(即滑動速度)與該點切向速度的比值稱為滑動系數,用η表示[8]。齒輪1的滑動系數為:η1=(vt2-vt1)/vt1;齒輪2的滑動系數為:η2=(vt1-vt2)/vt2。
齒輪嚙合傳動時,齒廓接觸點的相對滑動將會引起齒輪的磨損,而相對滑動的大小又與齒廓曲線的性質有關。齒輪傳動一般既有滾動又有滑動,齒輪的齒根滑動系數大于齒頂的滑動系數;小齒輪滑動系數大于大齒輪滑動系數。
2 直線共軛內嚙合泵幾何分析范例
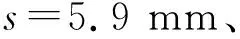
根據已知條件分析可知內齒輪2節圓半徑rj2=34.667 mm、傳動比i12=1.3,整體尺寸如圖5所示。
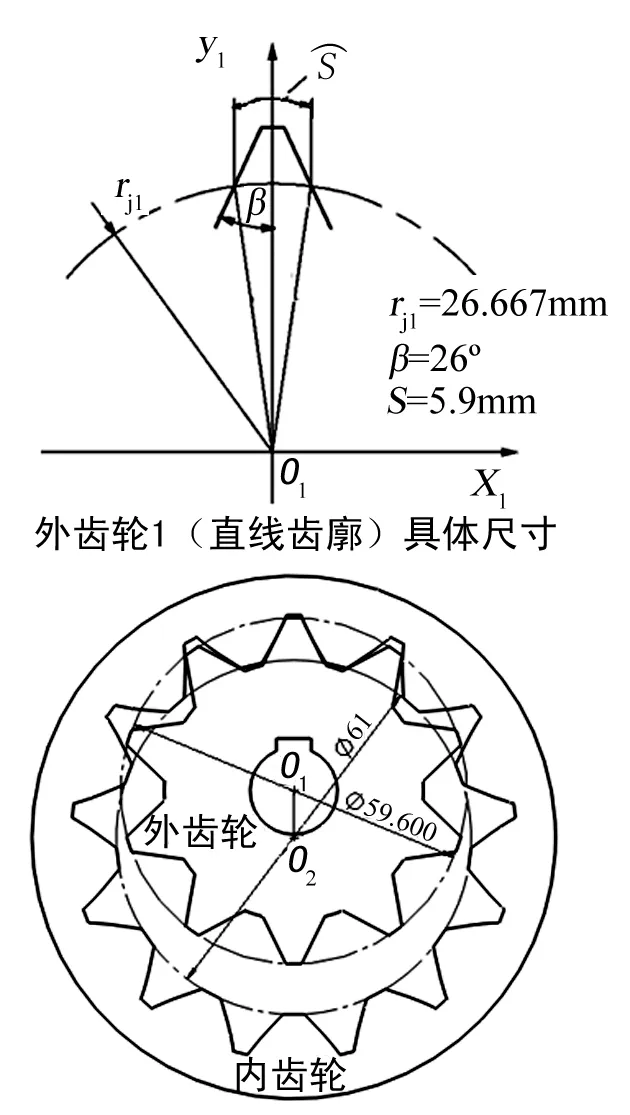
圖5 經典直線共軛內嚙合齒廓整體尺寸
根據理論分析,外齒輪1齒廓為直線,可作圖求解其基圓半徑,如圖6所示,可知齒輪1基圓半徑為O1F=14.264 mm,O1O2=8 mm(圖中可省略兩尺寸)。
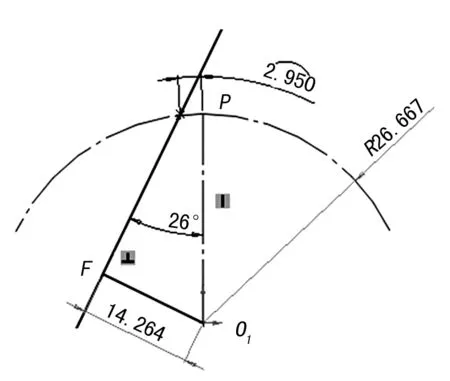
圖6 作圖求解直線齒輪基圓半徑
2.1 嚙合角求解過程
(1) 根據1.3節嚙合角定義,角θ為嚙合角,建立幾何模型如圖7所示。

圖7 嚙合角幾何模型
(2) 保持模型幾何關系,以嚙合點E點的X坐標為驅動尺寸,嚙合角θ角為從動尺寸,結合Excel軟件,驅動尺寸間隔設置為0.01 mm(以下同),獲得關系曲線如圖8所示。

圖8 嚙合角變化分析
(3) 從c點到d點的嚙合過程中,嚙合角的值逐漸變大,c點嚙合角為最小值11.14°(X方向值為-8.94 mm),d點嚙合角為最大值48.95°(X方向的值為3.84 mm),嚙合角平穩過渡無突變,兩極限位置嚙合角分析如圖9所示。
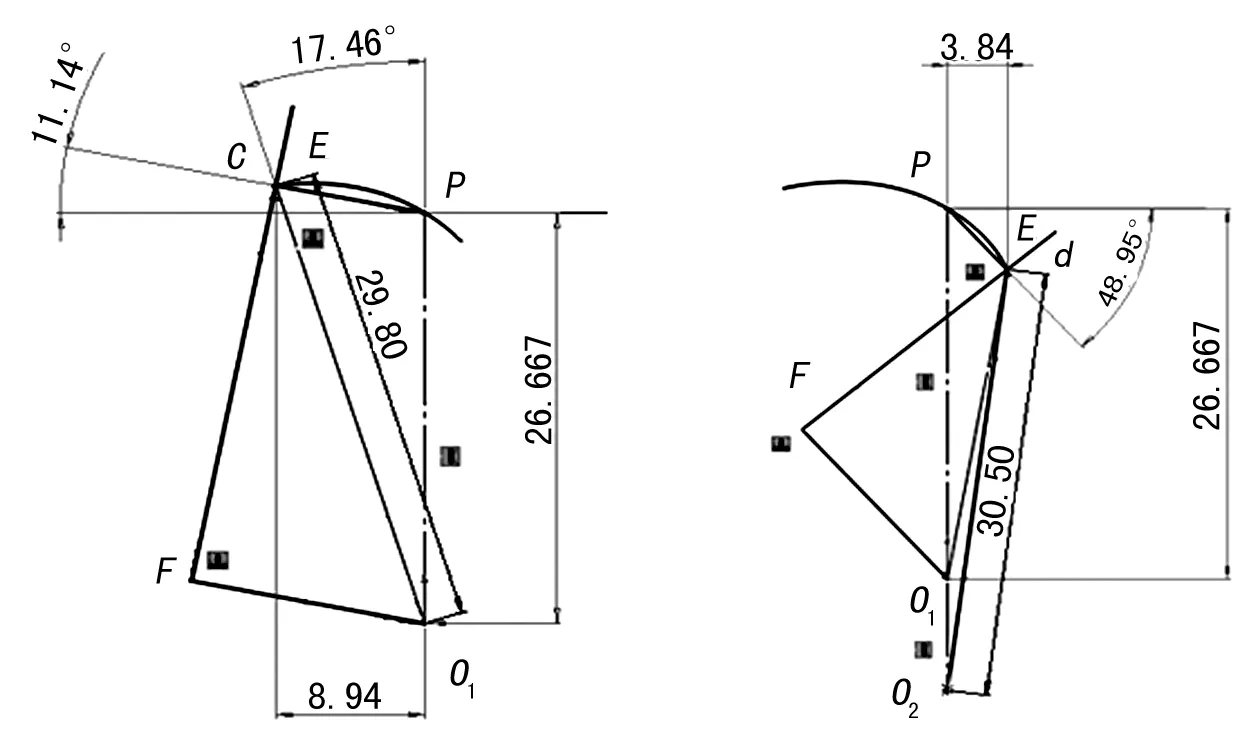
圖9 兩極限位置的嚙合角
2.2 壓力角求解
(1) 根據1.4節定義,如圖10所示,角α即為齒輪1的壓力角。
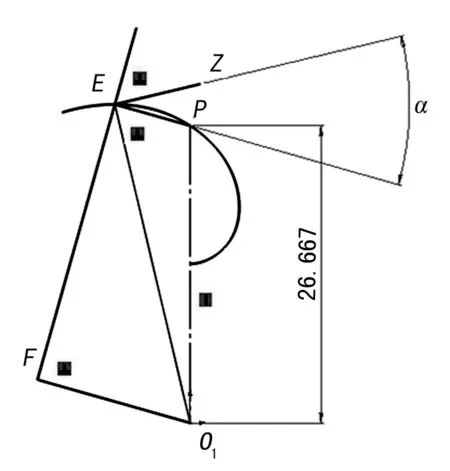
圖10 壓力角幾何模型
(2) 保持模型幾何關系,以嚙合點E點的X坐標為驅動尺寸,壓力角α為從動尺寸,結合Excel軟件,關系曲線如圖11所示。
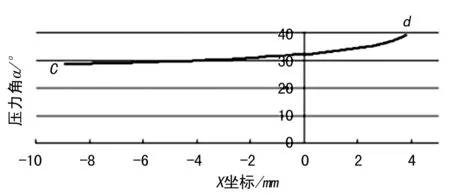
圖11 直線齒輪1壓力角曲線
(3)E點從c點到d點的嚙合過程中,齒輪1壓力角逐漸變大,c點的壓力角為最小值28.60°,d點的壓力角為最大值39.17°,壓力角的過渡平穩無突變,兩極限位置壓力角分析如圖12所示。
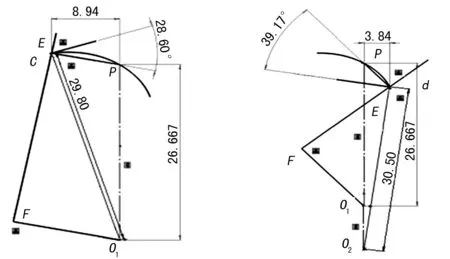
圖12 兩極限位置的壓力角
2.3 滑動系數求解
(1) 根據1.5節定義,過嚙合點E點作O1E與O2E的垂線,與直線EF(為嚙合的切線)的夾角分別為δ1和δ2,O1E為嚙合半徑R1,O2E為嚙合半徑R2,如圖13所示。
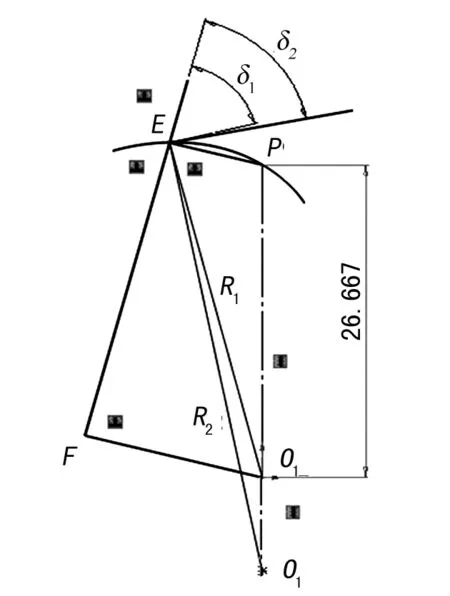
圖13 滑動系數的幾何模型
(2) 根據滑動系數的定義,vt1=ω1R1cos(δ1);vt2=ω2R2cos(δ2),ω1為齒輪1轉動的角速度;ω2為齒輪2轉動的角速度,將傳動比關系ω1=1.3ω2代入公式,則η1=(vt2-vt1)/vt1=R2cos(δ2)/[1.3×R1cos(δ1)]-1。根據公式,只要查詢嚙合E點cd段任一位置的R1、R2、δ1和δ2四個值導入Excel軟件,通過公式即可求出滑動系數,滑動系數關系曲線如圖14所示。
由于E點公切線方向速度值不同從而引出了滑動系數,在公法線上方向上速度的值應該相同(否則會出現脫離的現象),在Excel中進行計算η法=vt2/vt1=R2sin(δ2)/[1.3×R1sin(δ1)],計算結果皆為1,如圖14所示,說明法向的速度相等。

圖14 Excel中計算齒輪1滑動和法向系數
(3) 從c點到d點的嚙合過程中,滑動系數η1逐漸變大,c點的滑動系數為-0.14 742;兩節圓交點處滑動系數為0;d點滑動系數0.094 585,滑動系數的過渡平穩無突變。如圖15所示。
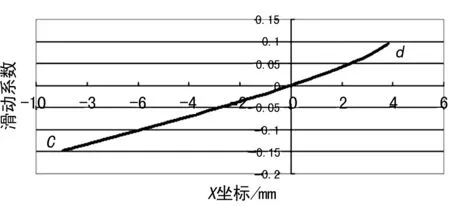
圖15 齒輪1滑動系數變化曲線
間隔根據需求可在Excel中任意設定,但不能超過其嚙合范圍,否則它的幾何模型無法生成。范例中僅僅求解齒輪1的壓力角和滑動系數,同理可求解齒輪2,文中在此不再闡述。
3 結 論
文中重點針對直線共軛液壓泵齒輪齒廓嚙合參數缺乏統一系統分析的問題,使用了幾何方法對其嚙合參數進行分析,揭示了內在的動態嚙合規律,對直線共軛齒輪齒廓設計有一定參考價值,總結重點如下。
(1) 同樣可用參數化草圖分析其嚙合極限半徑等其它嚙合參數,文中并沒有進一步展開。
(2) 基于Willis定理構建的直線共軛齒輪幾何嚙合模型簡潔準確且高效,根據其幾何模型求解嚙合參數,比單一公式計算有著先天的優勢。
(3) 使用參數化CAD軟件省去了繁瑣的計算,并且可動態分析整個嚙合過程,更適合工程人士使用。
(4) 對直線共軛齒輪嚙合參數的研究為進一步研究直線共軛齒輪的流量、功率、阻力等設計奠定了基礎。
(5) 所提幾何分析方法不但可求解直線共軛齒輪,也可求解其它類型的共軛齒輪。
(6) 通過對直線共軛齒輪嚙合幾何模型分析可知嚙合角、壓力角、滑動系數等嚙合變化規律,但作為齒輪泵不但要考慮傳動特性還需考慮困油、流量等因素。

