一道課本練習題的再思考

張富慶

【摘要】 課本是重要的數學資源，課本中的例題、習題是教材編者精心挑選的具有代表性的一些問題，是理解概念、性質、判定并學會運用它們解決問題的助推器，其蘊含著豐富的數學思想和數學方法，有廣闊的內涵和外延，是中考乃至其他命題的重要題源，故應該對一些重要的例題、習題進行再思考，挖掘出一系列結論，感悟典型例題習題的再生性，體現課本習題的潛在功能，實現課本資源利用最大化.

【關鍵詞】 課本練習;再思考

題源 有這么一道習題：如圖1，△ABC和△CDE是等邊三角形，△EBC可以看做是△DAC經過平移、軸對稱或旋轉得到，試說明得到△EBC的過程.

這道數學練習題實際上是運用旋轉思想讓學生說明△DAC是如何得到△EBC的！比較容易理解，我們可以對這道練習題進行再思考，挖掘其他一些有價值的結論！

1 挖掘其他三角形全等

本題不管是運用三角形全等還是旋轉知識去解釋，都能得到結論△ADC≌△BEC，事實上我們還可以挖掘出其他一些全等三角形，如△APC≌△BQC和△DPC≌△EQC（在這不贅述證明）

結論1 △APC≌△BQC和△DPC≌△EQC.

2 挖掘相關線段、角的結論

根據三角形全等性質，很明顯容易想到一些線段或角相等的結論，由△ADC≌△BEC顯然容易得出：

結論2 AD=BE，∠1=∠2，∠3=∠4.

同理根據△APC≌△BQC和△DPC≌△EQC，也容易得出：

結論3 AP=BQ，PC=QC，PD=QE，

∠APC=∠BQC，∠DPC=∠EQC，

∠ACP=∠PCQ=∠QCE=60°，∠POQ=120°.

如果繼續再連接OC，根據△APC≌△BQC，所以△APC和△BQC的面積相等，又AP=BQ，顯然由等面積法可得出這兩邊上的高相等，所以根據角平分線的判定定理很顯然CO平分∠POQ.

結論4 OC平分∠POQ或∠POC=∠QOC=60°.

3 挖掘特殊三角形和線段的特殊位置關系

順著上面的思路，根據三角形全等知識，如果連接PQ，顯然可以發現△PCQ是等邊三角形，也就說∠ACP=∠QPC=60°，

即PQ∥AE.

結論5 △PCQ是等邊三角形.

結論6 PQ∥AE.

4 挖掘四點共圓

我們知道，證明多點共圓，常有三種處理策略：

一是依據圓的定義，即證明動點到某點是定值（定點對定長）.

二是逆用圓周角性質，即證明動點對一定線段的張角為定值（定弦對定角）.

三是利用四邊形中如果對角互補，那么該四邊形四個頂點共圓.對于本練習題，我們進一步思考挖掘，可以發現該圖形中蘊含著多個四點共圓的知識（結論7、8）.

我們知道，在△PBO和△PAC中，∠1=∠2，∠BPO=∠APC，顯然根據三角形內角和定理，我們可以發現∠BOP=∠ACP=60°，

所以∠POQ+∠PCQ=120°+60°=180°，

即四邊形OPCQ的四個頂點共圓.

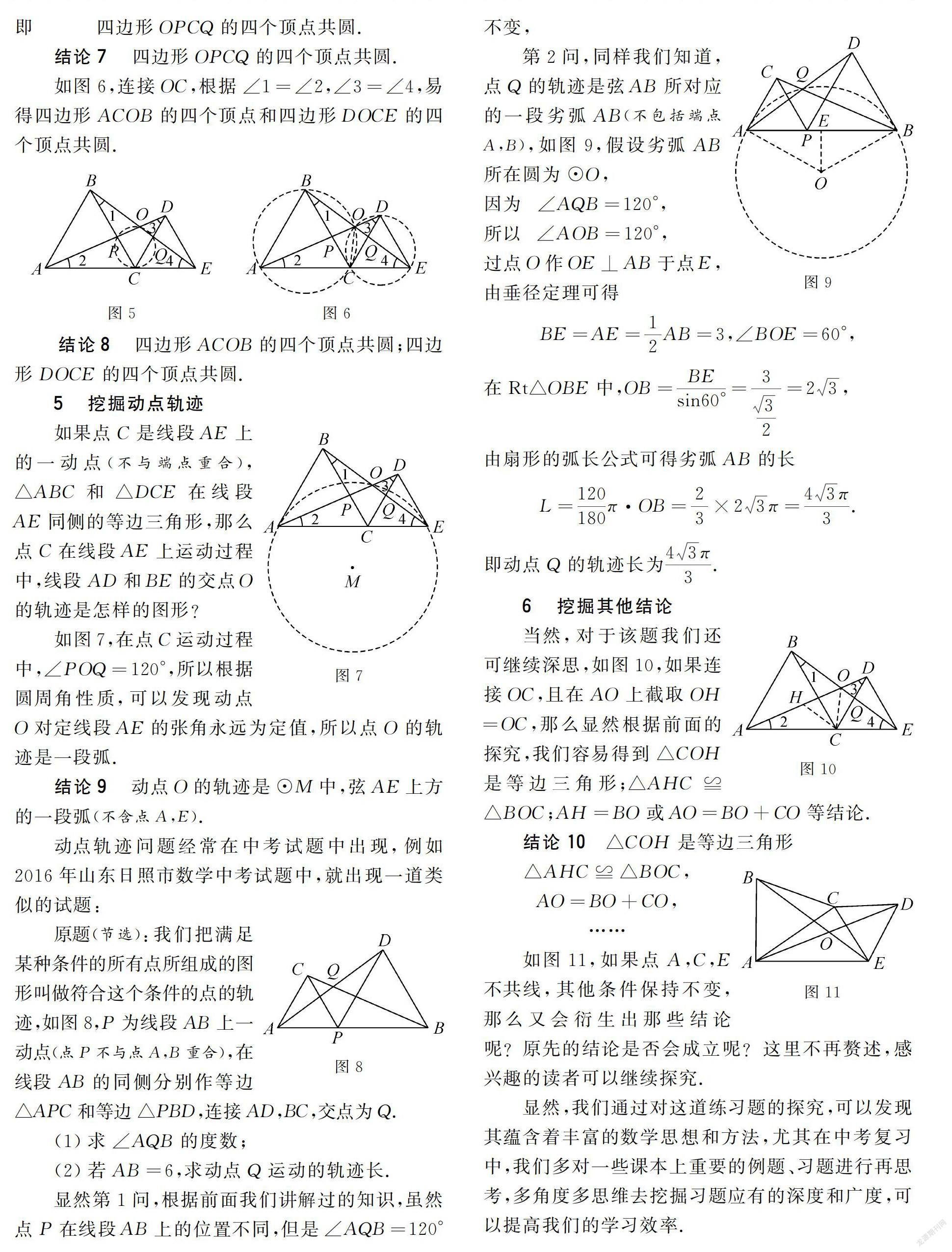
結論7 四邊形OPCQ的四個頂點共圓.

如圖6，連接OC，根據∠1=∠2，∠3=∠4，易得四邊形ACOB的四個頂點和四邊形DOCE的四個頂點共圓.

結論8 四邊形ACOB的四個頂點共圓;四邊形DOCE的四個頂點共圓.

5 挖掘動點軌跡

如果點C是線段AE上的一動點（不與端點重合），△ABC和△DCE在線段AE同側的等邊三角形，那么點C在線段AE上運動過程中，線段AD和BE的交點O的軌跡是怎樣的圖形？

如圖7，在點C運動過程中，∠POQ=120°，所以根據圓周角性質，可以發現動點O對定線段AE的張角永遠為定值，所以點O的軌跡是一段弧.

結論9 動點O的軌跡是⊙M中，弦AE上方的一段弧（不含點A，E）.

動點軌跡問題經常在中考試題中出現，例如2016年山東日照市數學中考試題中，就出現一道類似的試題：

原題（節選）：我們把滿足某種條件的所有點所組成的圖形叫做符合這個條件的點的軌跡，如圖8，P為線段AB上一動點（點P不與點A，B重合），在線段AB的同側分別作等邊△APC和等邊△PBD，連接AD，BC，交點為Q.

（1）求∠AQB的度數;

（2）若AB=6，求動點Q運動的軌跡長.

顯然第1問，根據前面我們講解過的知識，雖然點P在線段AB上的位置不同，但是∠AQB=120°不變，

第2問，同樣我們知道，點Q的軌跡是弦AB所對應的一段劣弧AB（不包括端點A，B），如圖9，假設劣弧AB所在圓為⊙O，

因為∠AQB=120°，

所以∠AOB=120°，

過點O作OE⊥AB于點E，由垂徑定理可得

BE=AE=12AB=3，∠BOE=60°，

在Rt△OBE中，

OB=BEsin60°=332=23，

由扇形的弧長公式可得劣弧AB的長

L=120180π·OB=23×23π=43π3.

即動點Q的軌跡長為43π3.

6 挖掘其他結論

0

當然，對于該題我們還可繼續深思，如圖10，如果連接OC，且在AO上截取OH=OC，那么顯然根據前面的探究，我們容易得到△COH是等邊三角形;△AHC≌△BOC;AH=BO或AO=BO+CO等結論.

結論10 △COH是等邊三角形圖11

△AHC≌△BOC，

AO=BO+CO，

……

如圖11，如果點A，C，E不共線，其他條件保持不變，那么又會衍生出那些結論呢？原先的結論是否會成立呢？這里不再贅述，感興趣的讀者可以繼續探究.

顯然，我們通過對這道練習題的探究，可以發現其蘊含著豐富的數學思想和方法，尤其在中考復習中，我們多對一些課本上重要的例題、習題進行再思考，多角度多思維去挖掘習題應有的深度和廣度，可以提高我們的學習效率.