基于改進啟發式搜索算法的智能電網電能質量監控

龍薔

(凱里學院， 建筑工程學院, 貴州， 凱里 556000)

0 引言

智能電網是一種隨著計算機、嵌入式、通信等技術發展而興起的新型系統。其核心思想是將電力傳輸與分布式網絡通過傳感器、計算單元以及通信網絡相連接，提供了更加靈活、高效的電能管理方式。智能電網的概念一經提出，就備受學者的廣泛關注。

智能電網最重要的一個特征就是自愈能力。然而，要實現自愈能力的關鍵就是要提高電能質量監控(Power quality monitor，PQM)效率。一種解決思路是對電網各節點添加電能監控模塊，從而提高電能質量監控能力。考慮到成本以及效率問題，不能簡單地對電網無限制添加或減少質量監控模塊，因此探索智能電網中監控模塊數量以及安裝位置的優化問題成為制約智能電網質量監控發展的重要因素，這也是困擾眾多學者的難點。

目前，已有眾多國內外學者對智能電網電能質量監控進行研究，并取得了一定成果。陳實[1]提出了一種改進的電能質量分析建立電能質量監控系統。該系統能夠便捷地分析和檢測各類電能質量干擾，如基頻偏差、諧波、相間諧波、電壓波動以及電能質量事件等。杜俊杰等[2]提出了一種能夠對諧波超標進行聯動預警與控制的軟件邏輯算法。該算法在保障用戶設備安全的前提下實現對用戶諧波的有效監控，保證了電網母線諧波控制在國標范圍之內。上述方法在對電能質量監控時未考慮最優解，而僅僅是找到了一個可行解。C. Ammer等[3]提出了一個基于回歸分析的節點檢測算法，能夠對各節點的相似行為進行評估，從而找出冗余電能質量監控支路。該方法在一定程度上能夠減少電能質量監控的數量，但是由于算法是基于大量數據進行分析得到，結果的準確度有待進一步驗證。Kaushal J等[4]提出一種利用MATLAB-Simulink軟件對單相交流微電網電能質量相關的電參數包括電壓、頻率、功率因數和總諧波失真等進行評估的決策方法。為了量化電能質量隨機變化的模糊性，利用256個基于規則的模糊推理系統對單相微電網模型提出了電能質量監測指標(PQMI)。該方法引入了模糊規則從而進一步精細化電能質量監控指標，然而模糊指標選取合理與否將對結果產生重要影響。選取精度過低造成準確度無法達到實用要求；選取進度過大將對系統造成重大負擔。Kamyabi L等[5]提出了一種新的電力系統電能質量監測儀(PQMs)在不同的不可觀測深度下的定位方法。在該方法中，考慮到這些器件測量通道數目的限制，將放置問題分為兩個層次進行求解。在該方法的第一級，選擇不同的連接線組合，而第二級確定在不同的不可觀測深度處每個組合的監視器的最佳位置。此外，第二級還識別關鍵總線，并考慮它們對監控器數量和位置的影響。該方法以不可觀測母線上的電壓相量估計誤差最小以及裝置的成本最低為主要目標。因此，該方法將找到安裝監控器的最佳位置和這些設備所需的最少通道數，以使所有電能質量參數(即電壓和電流相量)可觀測。

目前大部分方法的研究重心都在可觀測性方面，偶爾會有兼顧定位及考慮安裝代價等，因此在實際應用時缺乏一定實用性。為解決上述問題，本文對智能電網中電能質量監控進行了研究，以可觀測、定位及安裝代價為目標函數，提出了一種改進啟發式搜索算法對優化模型進行求解。

1 電能質量監控模型

1.1 電能質量監控可觀測模型

電能質量監控的定位問題可抽象為經典數學中組合優化問題。具體描述為

s.t.DX≥b

(1)

其中，C為1×Nb的矩陣，表示在網絡節點中安裝質量監控設備的代價矩陣，Nb表示系統中節點的數量。X為一個1×Nb的0-1矩陣，元素0表示該節點不需要安裝電能質量監控設備，1表示該節點需要安裝電能質量監控設備。約束條件中，b為一個1×Nb常數矩陣，表示各電能質量監控設備安裝代價要求。D為電能質量監控設備的密度函數，可通過一個m×Nb的觀測矩陣A獲取，其中m表示觀測中的狀態變量。觀測矩陣的計算公式為

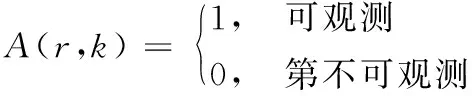
(2)

其中，r為觀測變量，k為電能質量監控設備個數。

值得注意的是，當一個智能電網網絡節點安裝電能質量監控設備后，與其相連接的鄰接網絡節點也可被觀測。接下來引入線路可觀測概念。

定義1 當網絡拓撲中一條邊的兩個節點都被安裝電能質量監控設備后，那么這條線路被稱為可觀測。

結合定義1，觀測矩陣可被進一步劃分為兩個部分：觀測節點與觀測線路，形式化描述為

(3)

其中，Av為NB×NB的觀測節點。Ai為NL×NB的觀測線路，且NL為線路個數。

因此，觀測節點矩陣形式化描述為

(4)

與之類似，觀測線路矩陣可描述為

(5)

1.2 電能質量監控定位模型

對于已觀測節點，即已安裝電能質量監控設備的節點很容易進行定位。然而對于未定位節點，需要進行快速定位，從而保證電能質量監控的效率。

為了優化系統中電能質量監控設備數量以及定位模型，觀測節點矩陣Av進一步計算為

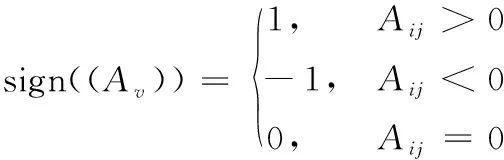
(6)

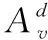
1.3 電能質量監控安裝代價模型

令dij表示智能電網節點i與節點j之間的距離矩陣。同理，距離矩陣也可用來描述電能質量監控設備節點i與節點j之間的電壓異常距離。

令dmin表示智能電網中距離矩陣dij最小距離。因此，隨著dmin的增大，系統安裝代價將快速增加。因此，系統安裝代價函數描述為

dmin≤C

(7)

其中，dmin為一常數值，C表示系統代價閾值。

2 解決方法

由于定位模型的基礎為可觀測，故可得知定位模型條件下的解一定為可觀測的。因此，為簡化計算，將可觀測模型與定位模型進行合并，同時結合安裝代價模型，本文提出了一種啟發式搜索算法用來求解電能質量監控面臨的定位以及安裝代價問題。啟發式算法將模型求解過程分為兩個部分，利用粒子群優化算法(PSO)分別找尋安裝代價以及定位問題的最優解。具體過程描述如下。

2.1 代價求解方法

本節將致力于尋求一個最小的安裝代價方法。首先，根據前述相關概念，電能質量監控設備的安裝代價模型為

costi=(NPQM×PPQM)+(Nch×Pch)+

(Nuch×Puch),i=1,2,…,NPop

(8)

其中，NPQM為安裝電能質量監控設備的數量，Nch為電能質量監控設備測量節點電壓的通道總數，Nuch為電能質量監控設備未使用的通道總數。同理，PPQM、Pch、Puch為電能監控設備、已使用通道和未使用通道的費用。

(9)

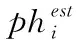
2.2 定位模型求解方法

令模型中總線數量為NBZ，通道數量為ch，則整體計算過程中系統變量尺度為NBZ×ch。根據前述規則可知，系統中評估誤差來源都來自未觀測到的網絡節點。令系統中未觀測到節點的數量為NPQM，則評估方程定義為

cost=[cost1,cost2,…,costNPQM]

(10)

同理，PSO算法更新規則方法為

c2r2[g(t)-xi(t)]

xi(t+1)=xi(t)+vi(t+1)

(11)

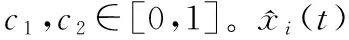
2.3 模型求解過程

結合2.1和2.2節內容，使用帶有啟發式搜索策略的PSO算法求解電能質量監控模型的具體過程如圖1所示。

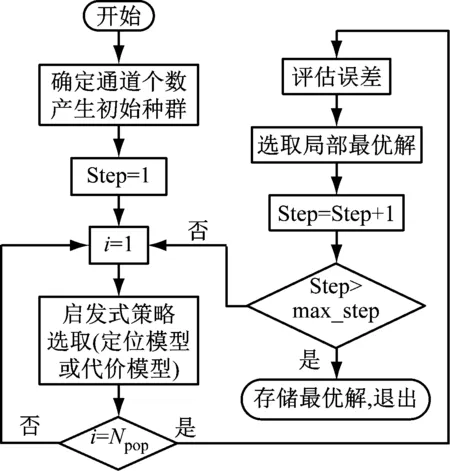
圖1 利用PSO算法求解安裝代價過程

算法過程可簡化步驟如下：

步驟1 初始化；

步驟2 迭代步長step=1，粒子i=1；

步驟3 啟發式搜索策略，分別帶入定位模型或代價模型；

步驟4 計算評估誤差；

步驟5 選取局部最優解，并更新方程；

步驟6 判斷是否達到退出條件。

3 仿真與分析

本節設計了一個仿真場景驗證本文所提方法的有效性。基礎場景參考了文獻[6]中IEEE 14總線模型。令仿真場景中節點分支個數為20個，電能質量監控設備為1個，設備安裝的位置為7號節點，且與之直接相連的節點有4、8和9號。電力仿真系統所中所設計的一些參數如表1所示。

表1 電力仿真系統參數信息

圖2為電力仿真場景中不同通道個數與安裝位置代價結果圖。

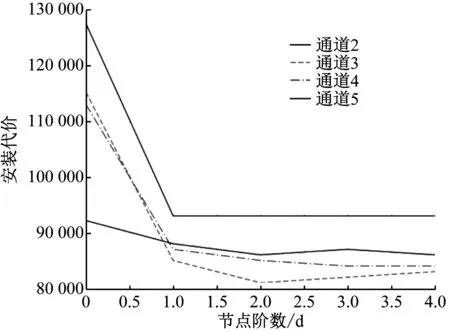
圖2 通道個數與安裝位置代價結果圖

由圖2可以看出，隨著通道個數增加，安裝代價呈現負相關關系。同時，當通道個數為3時，系統整體代價最優。

圖3為電力仿真場景中不同通道個數與定位模型代價結果圖。同理，當通道個數為3時，系統整體代價最優。

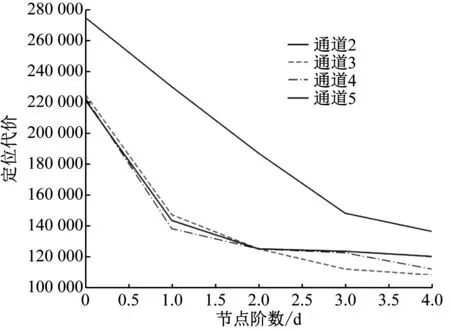
圖3 通道個數與定位模型代價結果圖

4 總結

為了應對智能電網中電能質量的監控問題，本文提出了一種改進的啟發式搜索電能質量監控優化系統，并對系統中PQM定位與代價尋優過程進行了詳細闡述。通過仿真分析，結果表明本文提出的方法能夠有效維護電力系統的正常運行。該結構為智能電網中電能質量監控的發展提供了一定借鑒和思路。