面向載荷運輸的非錨定空間系留電梯軌道半徑保持*
史格非
中山大學,廣州 510275
0 引言
空間系留電梯(Partial Space Elevator,PSE)概念源于“航天之父”齊奧爾科夫斯基提出的“太空電梯”構想。其總體結構如圖1。位于較高軌道的主航天器通過系繩將運輸航天器系留于較低軌道,通過電力驅動電梯艙內部爬行機構,實現負載電梯艙沿系繩的快速移動。該系統構建靈活,運輸成本低,安全性好,特別適于空間站物資運輸及面向超大型航天器在軌組裝的大范圍跨軌道載荷交換。其相關技術擁有廣闊的應用前景[1]。
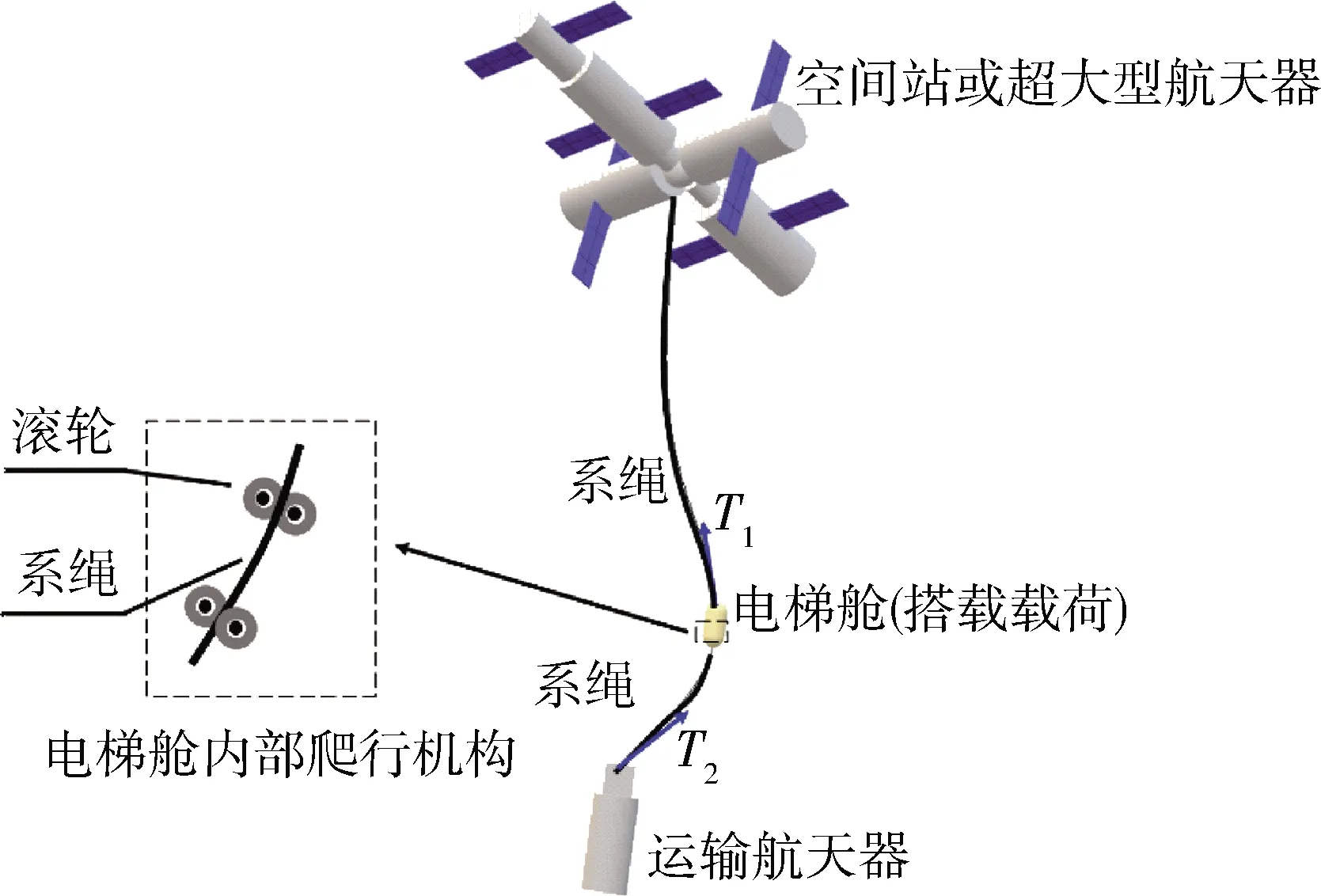
圖1 空間系留電梯系統總體結構
在載荷運輸過程中,系統各剛體間的動力學耦合將導致主航天器軌道參數發生變化,這不利于面向空間站及超大型航天器的貨物運輸。因此,如何將主航天器保持在目標軌道上,尤其是保持固定的軌道半徑,是空間系留電梯面向貨物運輸工程實踐的一個關鍵問題。
在過去的幾十年里,許多學者都致力于空間系留電梯(PSE)的動力學和控制方法的研究。Misra等[2]和Lorenzini等[3]給出了空間系留電梯的數學模型。Cohen等[4]、Woo等[5]和Williams等[6]研究了PSE的動力學特性。Yamagiwa等[7]從工程角度研究了PSE。Kojima等[8]提出了“任務函數”控制方法,僅通過調整電梯艙移動速度來抑制貨物運輸過程中的系統擺動。史格非等[9]借鑒文獻[10],系統地研究了PSE的擺動動力學,提出了不使用推力的擺動抑制策略。進一步,文獻[11]提出了一種控制非平衡欠驅動系統的“并行優化軌跡規劃與跟蹤”控制方法。上述工作皆假設主航天器錨定于固定軌道上。針對更為實際的情況,Jung等[12]建立了主航天器非錨定的PSE動力學模型,并對主航天器軌道半徑的變化特性進行了初步分析,但相關問題依然有待進一步研究。到目前為止,對于非錨定PSE的軌道半徑保持問題的研究非常有限,但依然可以借鑒部分現有的控制策略。鐘睿和朱正宏[13]提出了一種分段最優控制方法來控制電動力繩系衛星系統的軌道參數和姿態。相關的優化方法可用于處理欠驅動空間多體系統,包括非錨定PSE。除了最優控制方法外,模糊控制也是控制PSE的一種可能方法。考慮到軌道和姿態控制的要求,Rao等[14]提出了一種基于模型預測控制的“三階段”控制策略,用于對欠驅動繩系系統進行離軌控制。由于這種方法的泛用性和可實現性,可以考慮將其用于PSE的軌道保持及擺動抑制。
本文的研究目的是在不使用推力的情況下,實現對非錨定PSE在貨物運輸過程中主航天器的軌道半徑保持。首先,擴展經典的“兩啞鈴模型”,建立空間系留電梯動力學模型。在平衡特性分析的基礎上,提出了一種新的自穩定修正律。進一步,基于自穩定修正律,提出了一種新的控制策略并與SHMPC融合,在抑制系統擺動的同時,實現了主航天器軌道半徑的保持。仿真結果表明,所提出的控制策略適應貨物運輸任務的特點,效果良好。
1 動力學建模與分析
非錨定空間系留電梯簡圖及狀態參數如圖2:
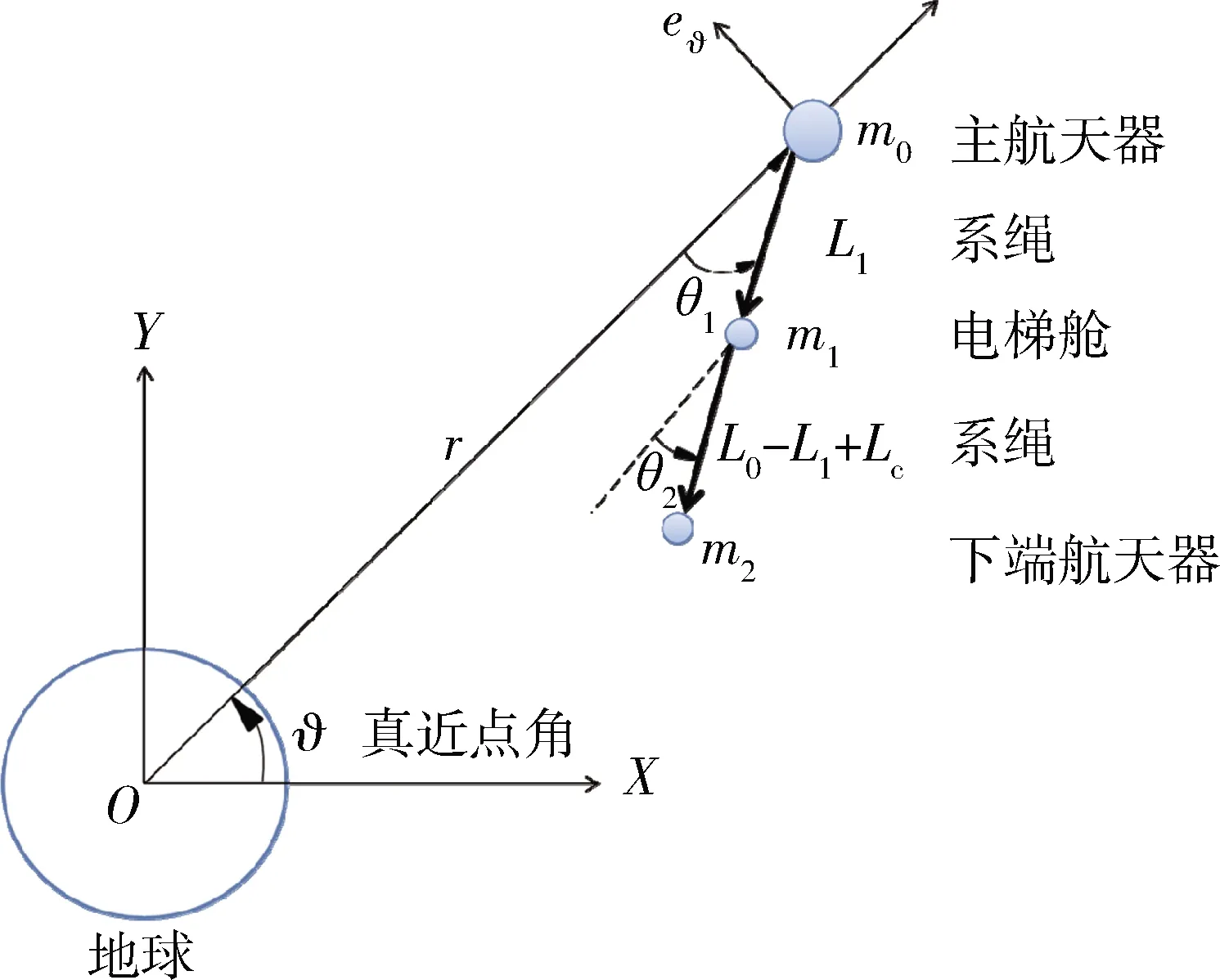
圖2 系統簡圖及狀態參數
為了簡化模型,假設系統處于一個無擾動的中心引力場中,忽略大氣阻力、太陽光壓、面外運動、系繩質量和彈性[15]。動力學模型建立在地心慣性系O-XY中。采用拉格朗日方程建立系統動力學模型,得到系統的六自由度動力學方程:
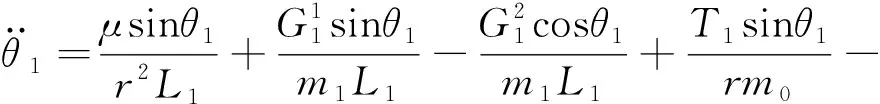
(1)
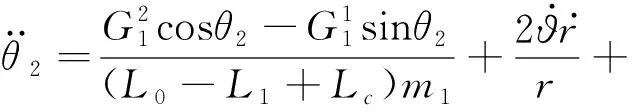
(2)
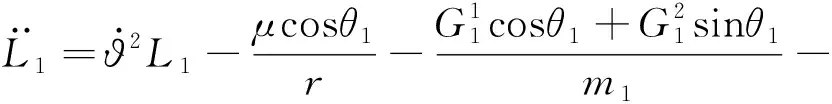
(3)
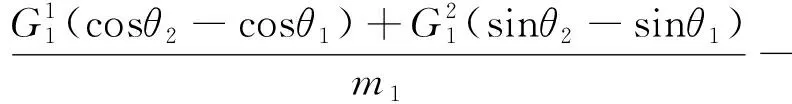
(4)
(5)
(6)
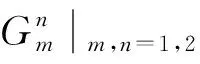
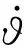
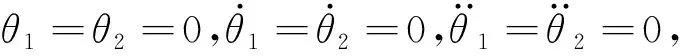
(7)
將式(7)代入系統動力學方程可以得到如下關系式:
(8)
(9)
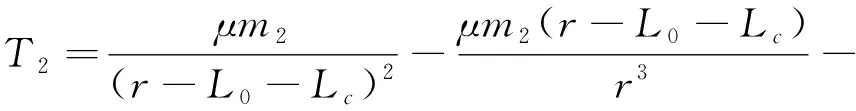
(10)
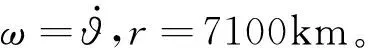
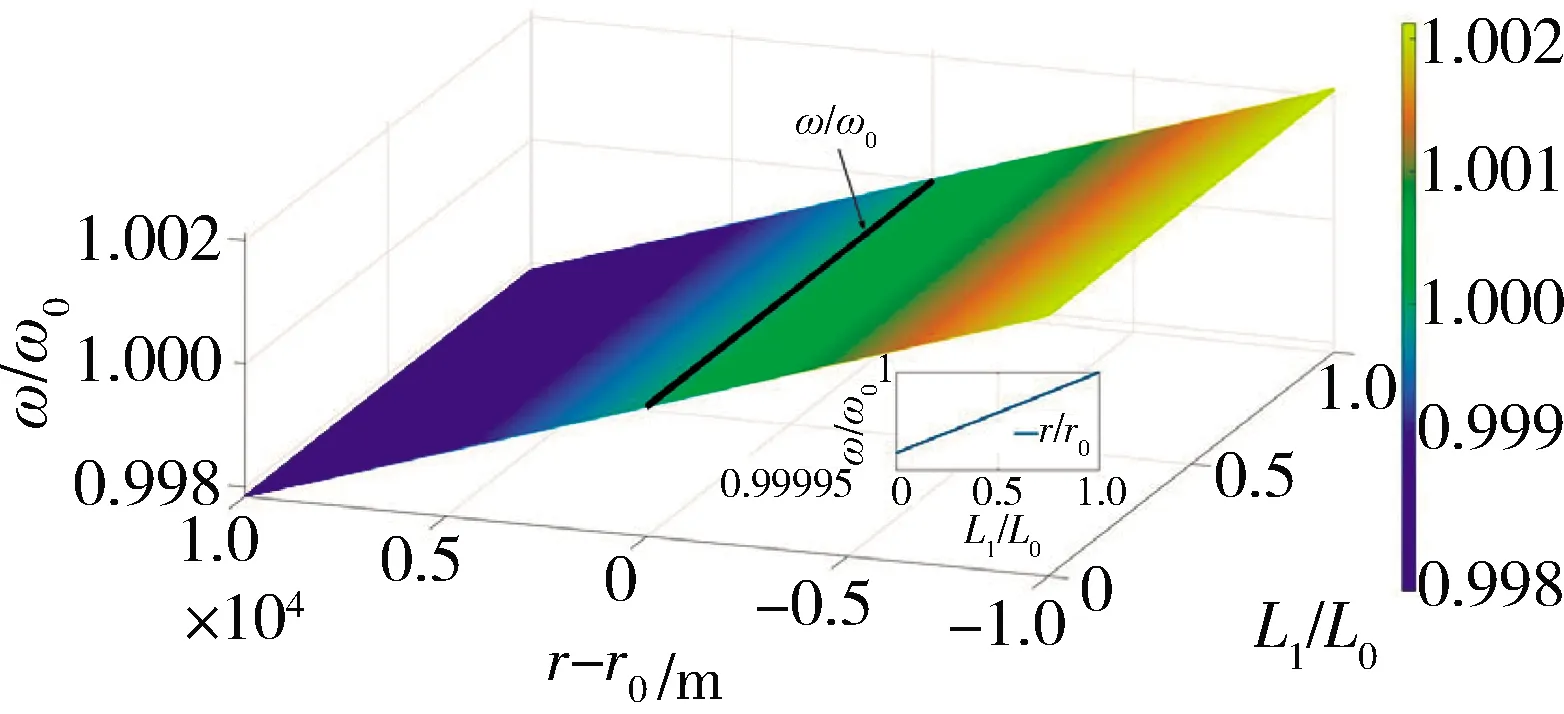
圖3 軌道參數平衡狀態
上述結果是基于系繩總長度不變的假設下得出的,即,Lc=0。在系繩總長度可變的條件下,對應不同的L1,可以得到特定軌道狀態下的平衡解:
(11)
平衡點解集如圖4中的實線表示。如圖4(a)所示,對應不同的L1,可以通過改變Lc進行平衡,其變化范圍為系統初始總繩長的45%~55%。在上述算例中,m1/m2=1/2,當該比值更小時,即電梯艙質量相比于下端系留飛船質量更小時,平衡解中的Lc減小,見圖4(b)。
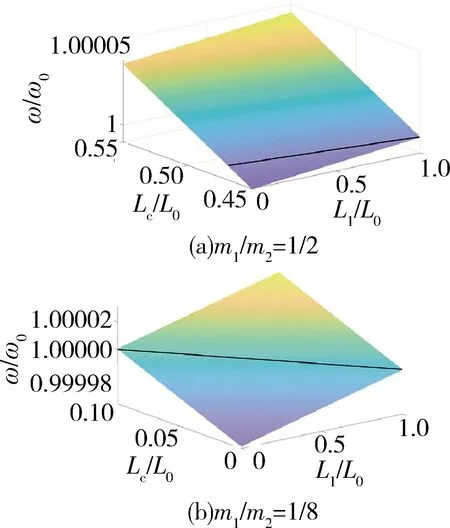
圖4 對應固定軌道半徑的平衡點軌道狀態參數
綜上所述,在平衡狀態下,對應電梯艙不同的位置,r/r0的變化量遠大于ω/ω0。此外,可以通過改變Lc,實現對非錨定的PSE的軌道保持,基于該結論,開展控制器設計研究。
2 控制器設計
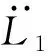
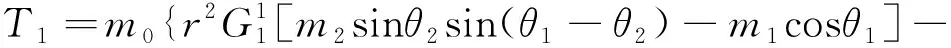
(12)
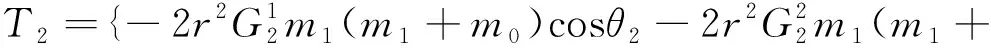
(13)
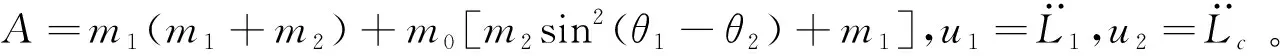
如式(5)所示,通過調節T1主航天器軌道進行保持的本質是對軌道半徑動力學方程的修正。因此,可以以T1為虛擬控制輸入,設計相應的修正律,實現主航天器軌道半徑的自穩定。將該自穩定修正律寫成滑模變結構控制律的形式,得到:
(14)
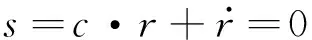
上述自穩定修正律可以看作是對控制輸入的一種約束。在該種約束下,通過調節u1和u2,可以對主航天器軌道半徑進行保持,并抑制非錨定PSE的擺動。由于貨物運輸是一個過程任務,故,要求系統狀態在任務結束時收斂到平衡狀態。對此,本文采用面向任務的SHMPC對系統進行控制。所預測的時域覆蓋從當前狀態到任務結束的時間段,控制時域則始終與預測時域成相同比例,當控制時域結束時,開始新的預測時域。本文忽略計算機運算時間。隨著控制近程的推進,預測時域越來越短,相應的控制時域也在縮減,這意味著越是接近任務結束,控制步長及其對應的周期就越短,控制精度也越高,這可以極好地應對空間系留電梯運輸任務所面臨的“面條”效應[8]。當預測時域小于一個設定閾值時,其對應的控制時域直接與其相等,即控制進入最后一個周期。在本文中,考慮PSE的運輸任務與系繩長度L1直接相關,因此控制時域直接以系繩長度作為尺度以代替時間尺度。這樣,每個控制步長結束時刻tf是浮動的,則當前控制周期的目標函數為:
(15)
服從公式(1)、(2)、(5)、(6)、(13)、(14)以及
(16)
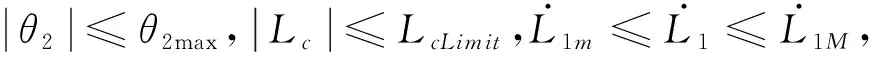
(17)
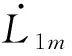
3 仿真校驗
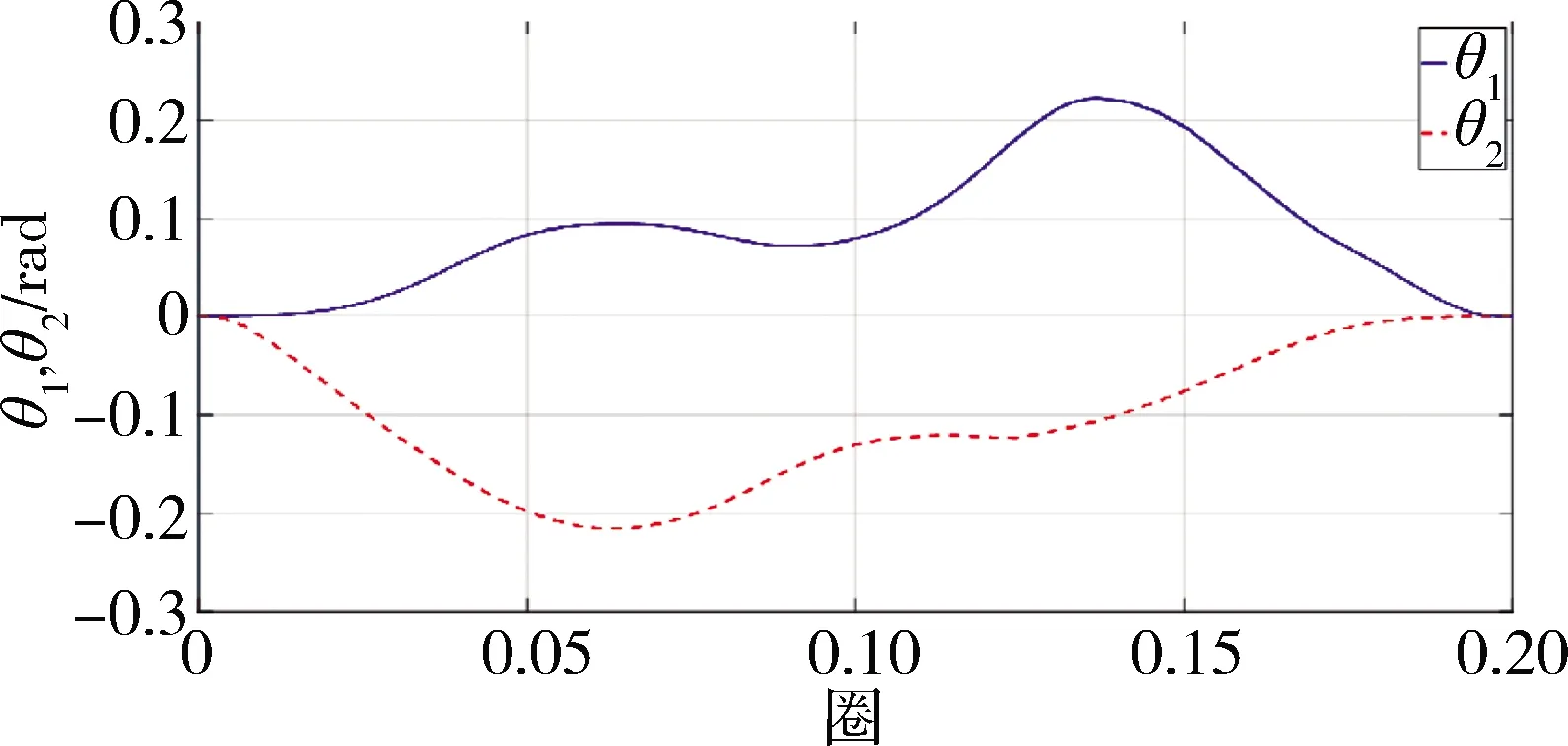
圖5 系統擺角變化
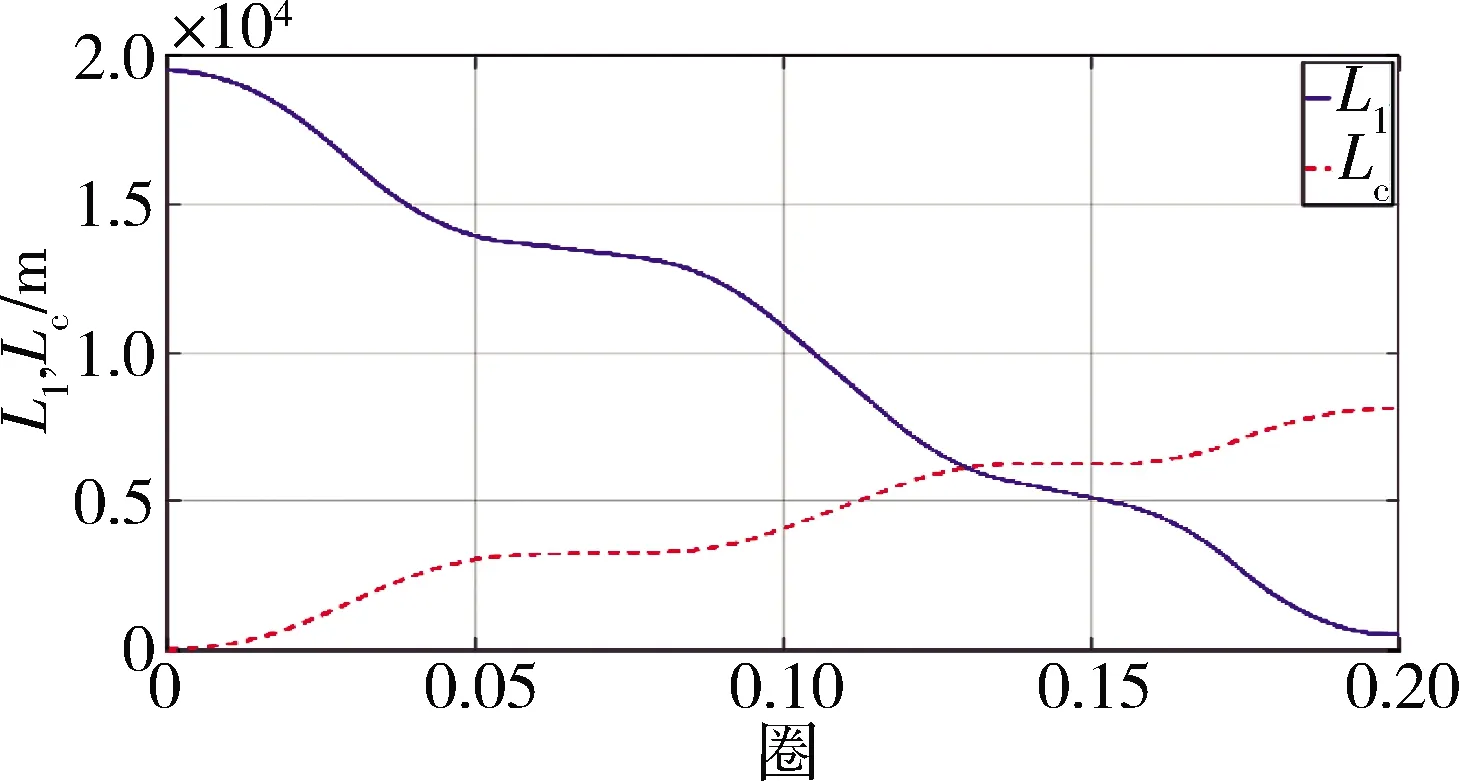
圖6 系繩長度變化
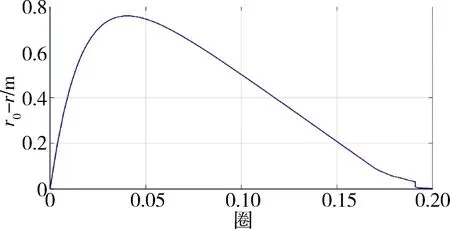
圖7 主航天器軌道半徑變化
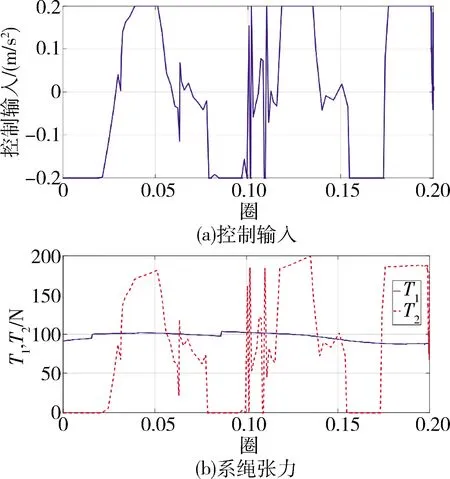
圖8 控制輸入與系繩張力
綜上所述,在自穩定修正律和比例SHMPC的作用下,可以實現對非錨定PSE的軌道保持,同時,也可以對系統擺動進行抑制。通過調節控制輸入,在運輸任務周期結束時,系統狀態參數將收斂到一個新的動態平衡狀態,而相應的,需要對下端飛船沿系繩向更低的軌道進行一定的釋放。
4 結論
本文基于六自由度動力學模型,對非錨定空間系留電梯的平衡狀態進行了分析。研究發現,為了保證對主航天軌道進行保持并使系統達到平衡狀態,可以沿系繩對下端飛船進行一定的釋放。受這一發現的啟發,本文提出了一種自穩定修正律,通過直接給定T1的修正律,實現對主航天器的軌道半徑保持。在此基礎上,面向保持軌道半徑和抑制擺動的需求,提出了一種新穎的控制策略。在此基礎上,考慮空間系留電梯貨物運輸任務特性,設計了基于比例SHMPC的控制律。仿真校驗結果表明,所提出的控制策略能夠在不使用推力的情況下,有效地實現主航天器的軌道半徑保持,并對系統擺動進行有效抑制。

