高溫季節軌道板溫度模型的熱流時延效應分析

方若望，何越磊，李再幃，路宏遙，趙彥旭

（1. 上海工程技術大學城市軌道交通學院，上海 201620；2. 中鐵二十一局集團有限公司，甘肅 蘭州 730070）

CRTSⅡ型板式無砟軌道作為我國高速鐵路重要組成結構，其混凝土結構破壞與溫度效應有重要關系[1]。 溫度作用力的劇烈變化會使軌道板產生諸多病害，常見的有裂縫、擠壓掉塊和翹曲變形[2-3]。 軌道結構在長期的溫度荷載變化下會產生不可逆轉的損傷，其中由于縱向的伸縮變形將導致寬窄接縫區域破損掉塊[4]，軌道結構整體升溫對軌道板與砂漿層界面開裂影響較大[5]，豎向溫度梯度是引起砂漿層界面離縫的主要原因。 諸多研究探討了溫度梯度對無砟軌道的結構特性影響。 鐘垚等[6]研究高溫條件及最高設計正溫度梯度下，軌道板與砂漿層之間仍會產生層間離縫且靠近板角位置更為嚴重。Song 等[7]提出了CRTSⅡ板式無砟軌道結構熱變形和界面分離的分析方法， 揭示了CRTSⅡ板式無砟軌道結構在自然環境條件下的溫度場、 熱變形、界面損傷和界面分離的特點。 劉鈺等[8]指出考慮熱效應引起的應力是正確設計結構的必要環節，提出了一種基于有限元方法的混凝土結構在時、空變溫度荷載作用下應力應變分析的數值方法。 現有的大部分研究[9-10]默認熱傳播速度無限大，系統時刻處于平衡狀態。 但在實際問題中，從狀態發生改變到建立平衡存在時間差，即由于溫度差異導致的熱傳遞具有延遲效應。本文以華東某線路CRTSⅡ型板式無砟軌道為例，研究環境溫度、太陽輻射等外界因素與軌道板自身內因對軌道板內部溫度分布的影響。 建立基于熱流時延的軌道板系統溫度模型，為后續在不破壞軌道結構的前提下評估軌道結構受力變形和維護提供理論依據。 包括指導施工作業，防止因破壞軌道結構產生巨大的溫度梯度及應力。

1 無砟軌道板內溫度分析

白天，軌道板表面由于外界環境因素升溫，并通過分子熱傳導向深處傳遞熱量；夜間，軌道板表面因與自然環境熱交換而首先冷卻， 熱量從板深處向上輸送。 軌道板溫度的變化首先從表面開始，逐漸影響深層板溫度的變化， 其變化幅度隨深度的增加而減少。 軌道板中熱量傳遞的大小與快慢還與板自身特性有關。 在自然科學土壤研究中[11]，若土壤是均質的， 其深處的傳熱僅通過分子的熱傳導， 而且土壤表面溫度隨時間有周期性變化，則土壤內溫度的變化遵循傅里葉定律：熱量轉遞愈深，則溫度周期變化的振幅衰減的越多；由溫度梯度引起的熱流之間的延遲時間與傳播距離成正比。

上述理念用公式展現，將其應用到軌道板溫度變化中，假設軌道板中混凝土是均質的，初步得到軌道板板內溫度簡易關系，即軌道板內部溫度由表層溫度曲線經過幅值變化和平移所得，結果如下

式中：T 為某一深度軌道板的溫度，K；τ 為軌道板不同深度溫度變化與軌道板表層的時間差，h；d 為深度，m； γ 為不同深度溫度幅值與軌道板表層的比值；T表為軌道板表層溫度，K；為表層平均溫度，K；為不同深度的平均溫度，K。

2 熱力學板溫求解模型

式（1）可大致反映出軌道板內溫度與板表的對應關系。 但是作為軌道板結構與外界環境的交界部位， 軌道板表層溫度受外界環境因素變化更為敏感，且存在突變的情形。 為了減少由于儀器自身原因或者記錄到的環境因素偶發變化帶來的影響，本文進一步考慮熱力學因素加入修正項來減少誤差。

2.1 太陽輻射

對監測的太陽輻射數據進行如下處理：先通過3 次樣條插值運算豐富數據量， 然后采用復化Simpson 公式對時間段求積分。 對前2 h 吸收的太陽輻射求均值， 作為該時間段影響軌道板溫度變化的太陽輻射量。 將區間 ［a，b］ 分成n 個子區間[xj，xj＋1]（j=0，1，…，n-1），第j 個子區間的中點為xj＋0.5，子區間長度為h。

應用復化Simpson 公式的太陽輻射求解公式如下

式中：f（a）為2 h 前的時刻測得的太陽輻射值，W/m2；f（b）為該時刻測得的太陽輻射值，W/m2。

2.2 熱對流

熱對流指的是在溫差的作用下，由流體的運動所引起的熱量傳遞。 通常為了方便起見，工程上采用牛頓冷卻定律[12]來計算混凝土表面與空氣的對流換熱密度，計算式為

式中：hc為對流傳熱系數，W/（m2·K），它取決于流體和固體表面的固有特性以及流體的速度分布，固體的溫度分布；Ts，Tu分別為軌道板表面溫度和空氣溫度，K。本文計算混凝土結構表面的對流換熱系數采用Saetta 等[13]給出的對流換熱公式，計算式為

式中：v 為風速，m/s。

2.3 熱輻射

任何具有溫度的物體，其熱能將通過電磁波的形式向外發射能量，這種現象稱之為熱輻射。 本文采用式（6）對軌道板混凝土表面熱輻射能量密度進行計算

式中：ε 為表面黑度， 對于混凝土可取0.94；σ 是黑體輻射常數，為5.67×10-8W/(m2·K4)。

2.4 熱流板溫模型

軌道板表層凈吸收的熱流密度如下

式中：q 為凈熱流密度，表示單位時間單位面積通過的熱量，W/m2；q1是太陽輻射密度，W/m2；q2是熱對流密度，W/m2；q3是熱輻射密度，W/m2。

以軌道板表層吸收的凈能量所能轉化的溫度量減去實際軌道板表層溫度的變化量，剩余部分作為修正項來減小誤差。

將軌道板溫度場計算假設為一維熱傳導問題，則軌道板內部溫度可大致看成是軌道板表層溫度曲線經過幅值放縮，相位延后所得。 由式（1）結合熱傳遞理論下的修正項，可得出軌道板板內不同深度溫度計算公式如下

式中：β 為能量轉化為溫度的轉化系數， 取0.004；ΔT表為表層溫度實測變化值，K。

以式（8）為核心計算公式，構成最終軌道板內不同深度溫度計算模型。區別于溫度擬合預測[14]，考慮了實時環境因素對軌道板內溫度帶來的影響，更有理論依據。 對于不同地區的軌道板內溫度變化規律，其幅值衰減γ 與延遲時間τ 有所不同。

3 熱流時延模型計算

以華東地區某高速鐵路2018 年7 月26 日到8月25 日期間測得的數據作為試驗計算驗證依據，數據內容包括風速、太陽輻射、環境溫度、軌道板表層及不同深度溫度等，數據收集間隔為0.5 h。 監測的板溫數據為路基軌道板板中位置， 具體位置如圖1 所示。

圖1 軌道板溫度監測位置示意圖Fig.1 Schematic diagram of track plate temperature monitoring position

3.1 實測軌道板溫度曲線

實測軌道板溫度曲線驗證了熱流存在時延，并且幅值衰減的理論（圖2）。

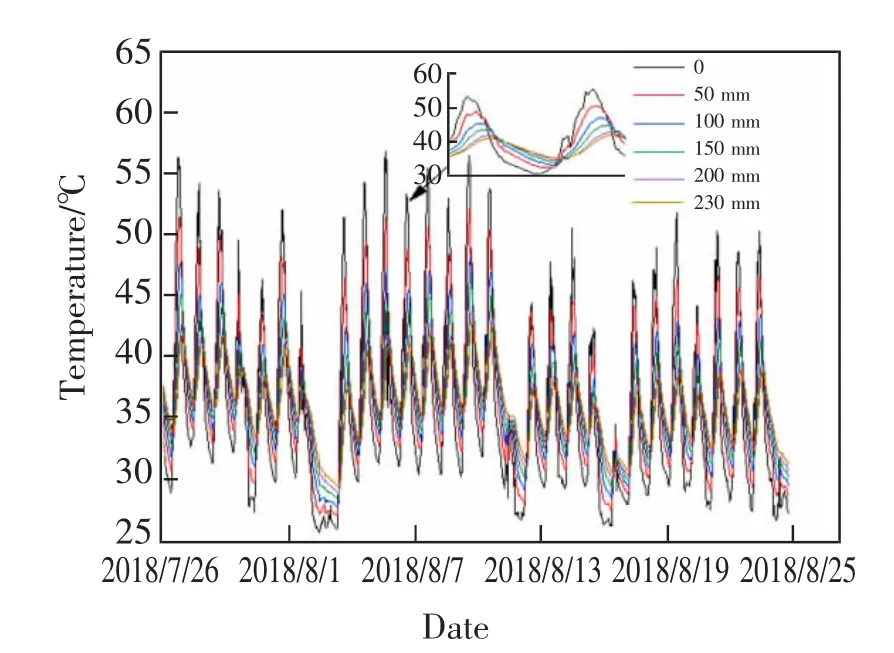
圖2 軌道板內不同深度溫度曲線Fig.2 Temperature curves of different depths in track slab

3.2 軌道板不同深度溫度頻域曲線

為了得出軌道板表層與不同深度溫度曲線關系的參數，采用頻譜分析的方法[15]，求出相應的τ，γ與深度d 的關系。 將測得的溫度數據傅里葉變換后，得到如圖3（a）所示頻域特性。 軌道板表層與不同深度溫度頻域特性相似，僅在頻率為1.158×10-5Hz時，溫度峰值有較大區別，對應的周期為23.99 h。其余頻率峰值相較于前者可忽略不計，本文僅考慮最大處峰值所蘊含的信息。若記表層溫度峰值為1，得到各深度峰值的擬合函數為

式中：γ 為軌道板各深度處溫度峰值相對表層的比值；d 為深度，m。 由式（9）可得出軌道板內各處溫度幅值隨深度呈指數衰減。

若記表層溫度峰值初始相位為0， 得到各深度溫度相位的擬合函數為

式中：φ 為軌道板各深度處溫度相對表層的滯后相位。 由式（10）可得出軌道板內各處溫度相位隨深度呈線性滯后。由圖3（c）相位差推時間差，得

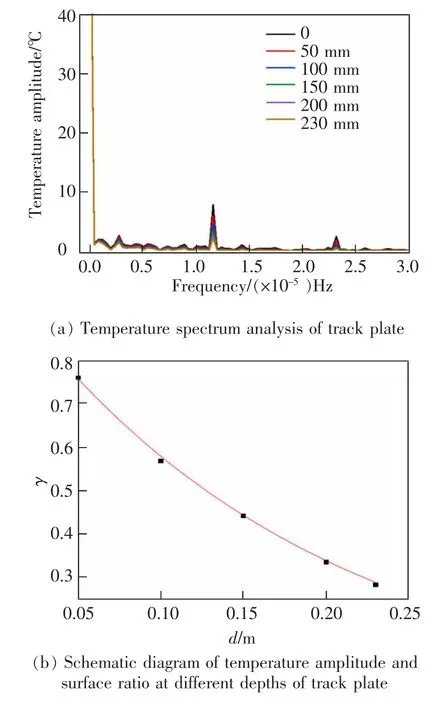
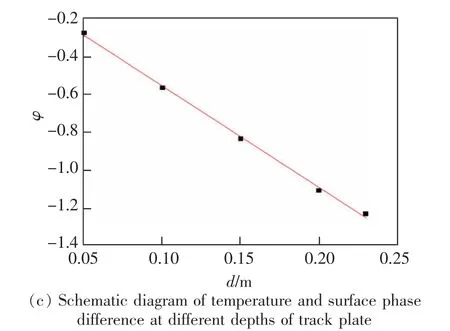
圖3 軌道板不同深度溫度頻域特征Fig.3 Frequency domain characteristics of temperature at different depths of track slab

式中：τ 為軌道板不同深度溫度變化相較于軌道板表面的時間差，h，負號代表延遲。

表1 不同深度溫度變化時間延遲Tab.1 Time delay of temperature change at different depths

上述頻域分析表明，軌道板不同深度溫度相對表層溫度序列，振幅以指數函數衰減，相位存在線性滯后。 同時也證明了無砟軌道板板內溫度熱流時延模型的可靠性。

4 熱流時延模型驗證

由本文熱流時延模型計算所得的不同深度溫度曲線與實測溫度對照展示如圖4。 由圖4 可以看出，最終求得的不同深度溫度曲線與實測溫度曲線吻合得較好，進而求出其平均相對誤差并進行可靠度分析（表2）。

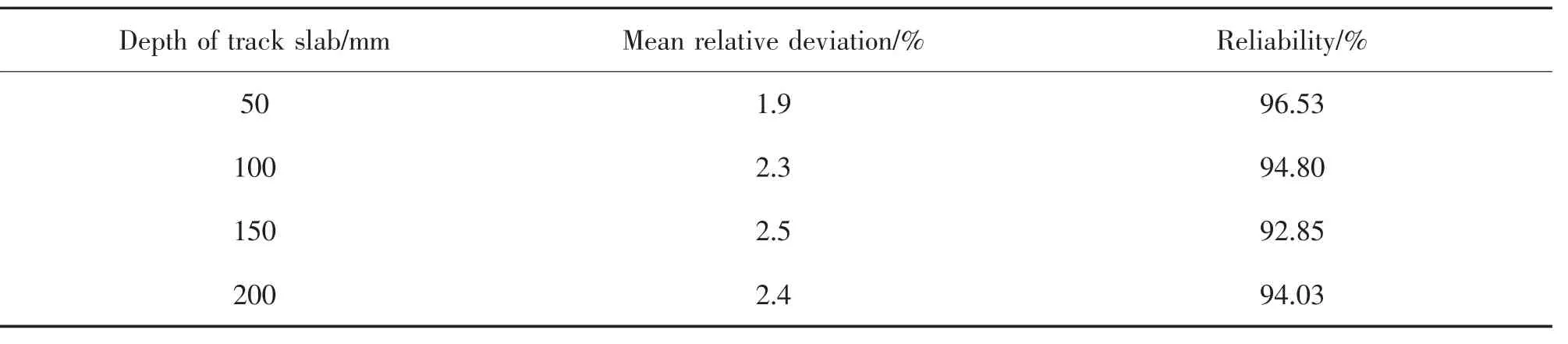
表2 計算所得溫度的平均相對誤差與可靠度Tab.2 Average relative error and reliability of calculated temperature

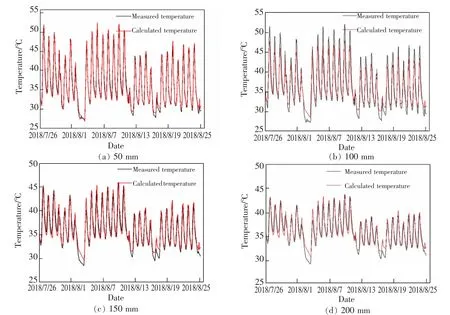
圖4 軌道板不同深度計算溫度對照Fig.4 Comparison of calculated temperature at different depths of track slab

計算求得的軌道板各深度溫度相對于實際溫度數據的平均相對誤差在1.9%～2.5%。 統計絕對誤差大于2 ℃的點占總監測點數的比例為D。 定義可靠度為1-D，結果顯示在92.85%～96.53%，滿足實驗要求。

5 結論

本文考慮輸入狀態發生改變到建立平衡存在時間差，把時間延遲引入到軌道板混凝土熱力學分析。 從溫度場作用于軌道板混凝土結構將改變其性能的點出發，分析了熱力學中不同的溫度傳遞方式以及熱流密度對軌道板內溫度變化的影響。 得出以下結論。

1） 對軌道板溫度進行頻譜分析得出軌道板內各處溫度幅值隨深度呈指數衰減， 溫度相位隨深度呈線性滯后。 熱量在軌道板中傳遞時， 每深入50 mm，軌道板溫度變化延遲時間約1.02 h。

2） 軌道板表面吸收的凈熱量除去部分轉化為內能，剩余量作為修正項避免了由于儀器自身原因或者記錄到的環境瞬態變化帶來的影響。 與對溫度擬合預測相比，考慮了實時環境因素對軌道板內溫度帶來的影響，更有理論依據。

3） 考慮了熱力學理論的溫度計算模型平均相對誤差在1.9%～2.5%， 可靠度在92.85%～96.53%，為后續在不破壞軌道結構的前提下分析軌道板應力及維護提供參考。

4） 為簡化模型，未考慮長期陰雨天溫度的復雜變化，期間會有較大誤差。