復合地層微型盾構機刀盤受力性狀及布置優化

蒲亞平

（中鐵十八局集團第一工程有限公司，河北 涿州 072750）

行業內通常把直徑小于3 m 的盾構機稱為微型盾構機[1]。 近年來，微型盾構已廣泛應用于廣東、福建等濱海省份城市的給排水隧道、 電力隧道、綜合管廊等市政工程領域中[2]，在城市建設中發揮著越來越重要的作用[3]。 而刀盤作為盾構機的關鍵部件[4]，刀盤的結構類型、刀具的數目及其布置會對刀具的使用壽命產生直接影響，進而影響整個盾構工程的安全性、經濟性和效率[5]。 為了確保微型盾構機在濱海復合地層條件下的正常掘進，對微型盾構機的刀盤設計和刀具的布置方法進行研究具有重要的工程意義。

目前國內外眾多學者對盾構機刀盤的設計進行了大量的研究。 Dahl 等[6]通過對Sievers 的J 微型鉆探測試方法的改進， 得到了直接估計刀具壽命的新方法，為刀具布局奠定了基礎。 蒲毅等[7]結合阿基米德螺旋線布刀法以及刀具磨損等壽命布刀原則，提出切刀應該對稱布置以適應刀盤正、反轉的實際使用需求， 為土壓平衡式盾構機刀盤面板上的刀具布置奠定了理論基礎。 學者利用改良的渣土具有“塑性流變狀態”的特性，采用CFD 流體軟件實現了刀盤結構動態切削仿真模型， 并通過研究刀盤的開口分布特性得到刀盤拓撲優化結構[8-9]。 Nilsen[10]通過有限元軟件采用靜力學板塊進行盾構刀盤結構強度驗算， 考慮在土體材料非線性的基礎上進行了刀盤動態仿真以及優化分析。田繼濤等[11]等人經過研究確定盾構刀盤的牛腿和法蘭盤的牛腿邊緣部位最為薄弱， 采用多目標遺傳算法優化了刀盤的幾何參數以及開口率， 為盾構刀盤結構優化提供了一定思路。 韓偉峰等[12]通過有限元軟件對盾構刀盤進行強度驗算以及模態分析， 采用蒙特卡羅抽樣技術對刀盤的設計缺陷之處進行優化設計， 從而提高了刀盤整體使用性能，而且還能夠達到減重降本的效果。 他們的研究主要針對實際施工中大型盾構機的刀盤、 刀具布置及仿真優化， 尚未對微型盾構機刀盤的結構參數進行系統性的優化設計。 而且，國內廠家在生產微型刀盤過程中往往是將大中型刀盤等比例縮小，這樣設計出的刀盤其選擇的刀具類型、數量及布置方法并不合理，并缺乏對地質狀況的分析，不利于整個盾構工程的安全性、 經濟性和工作效率[1]。如何解決微型盾構機的刀具布置單按比例縮小大型盾構機的刀盤結構這一問題成了微型盾構刀盤結構設計的一項關鍵技術。

除此之外， 微型盾構機在穿越濱海地層時盾構機刀盤與地層相適應性的研究尚未探明， 學者在利用盾構模型機探究盾構刀盤與地層相適應性時， 往往是量身定做并且只適用研究在單一的卵石、砂土、軟土、黏土層掘進過程中存在的問題[13-19]，對于軟硬不均、全～微風化花崗巖等濱海復雜地層需要多種模式的微型盾構機則顯得難以適用，并且盾構模型機對于刀盤、 刀具也只是簡單進行設計、布置，采用模型試驗得到的數據與理論值精度存在一定的差距。

本文以濱海復合地層為工程背景， 基于雙滾刀協同破巖原理確定最優滾刀間距， 對比分析3種整體式切刀布刀法的優劣， 通過動態仿真有限元模型確定最優刀盤結構， 并核驗了不同工況下的刀盤結構受力性狀， 有效解決微型盾構機的刀具布置單按比例縮小大型盾構機的刀盤結構這一問題，可實現小直徑盾構機對土體的全面切削，對濱海復雜地層中微型盾構機刀盤優化設計具有參考意義。

1 刀盤結構選型

刀盤作為機械化盾構的掘削機構，在盾構掘進過程中不僅承擔著開挖土體的作用，同時刀盤面板還可穩定掌子面，并且刀盤旋轉過程中會對渣土進行攪拌，改良渣土的塑性狀態，有利于排渣運土。 市場上刀盤結構的主流型式有3 種，即面板式、輻條式以及輻板式。 其中，輻板式刀盤不僅兼有面板式和輻條式的優點，整個刀盤面板上不僅可以看到較寬的輻條結構， 而且還能看到小塊的面板結構，其開口率通常為35%～50%[18]，切削類刀具對稱布置在輻條的兩側， 而滾刀直接安裝在輻條內部的刀座上，主要適用于復合地層。

濱海復雜地質條件可按復合地層來考慮，刀盤結構采用輻板式，開口率的取值范圍為25%～45%。為確定小直徑盾構機刀盤最佳結構型式，針對常用的三輻條三面板和四輻條四面板輻板式結構，分別建立四輻條四面板和三輻條三面板式刀盤結構的三維模型。刀盤直徑取600 mm，厚度選取40 mm，開口率40%， 整體刀盤結構不考慮刀具的精細化布置，可通過一定的刀刃代替切削刀具，并對刀盤施加一定的推力以及扭矩，通過分析刀盤結構的應力應變來進行優選。刀盤結構材料選擇Q345 鋼，采用四面體模型。 最終，依據靜力分析結果，四輻條四面板式刀盤結構的最大應力為21.92 MPa， 三輻條三面板式刀盤結構的最大應力達到了30.84 MPa，且四輻條式的刀盤面板比三輻條式的刀盤面板受力更均勻；因此，選用四輻條四面板式刀盤結構作為掘削刀盤。 同時，濱海地層巖性復雜，為了后續適應不同地層的掘進試驗，刀盤開口率進行了可變式設計，通過對輻板進行可拆卸式設計，從而達到調整開口率的目的。

2 刀盤布置設計有限元模擬

2.1 雙滾刀作用下協同破巖過程模擬

合適的刀間距可使滾刀在破巖過程中各自產生的裂紋相交從而加大巖石破碎量，提高滾刀破巖效率， 通過進行不同刀間距的雙滾刀破巖數值仿真，可為滾刀在盾構模型機的刀盤面板上進行布置時找到最優刀間距[19]。

巖石材料選取濱海地層的花崗巖，刀具選用已進行參數優選的滾刀刀圈， 分別建立圓心為參考點并與滾刀刀圈耦合成剛體約束， 滾壓速度為20 mm/s，滾刀轉速1 rad/s，切入深度2 mm，兩刀圈都同時以相同滾壓速度以及轉速進行破巖仿真，同時對模型底部采用全約束， 兩側采用進行對稱約束約束，以減少反射波的影響，并對中心區域的巖石單元進行網格加密，提高計算精度。

根據剪切破壞理論，巖石在滾刀破巖過程中形成破裂寬度a=P/tanα，如圖1 所示。其中在刀盤面板上相鄰滾刀的刀刃貫入度是一樣的，在刀盤面板上布置滾刀時， 相鄰滾刀之間的刀間距不能太大，以免形成巖脊未能完全切割整個開挖面，滾刀之間的刀間距應滿足

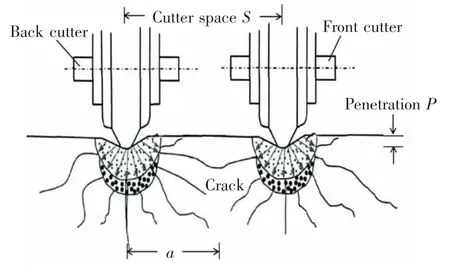
圖1 盤形滾刀破巖過程示意圖Fig.1 Schematic diagram of rock breaking process with disc cutters

式中：S 為刀間距；P 為貫入度；α 為巖石的壓裂角，通常為18°～30°，這里取29°；a 為巖石破裂寬度；b 為滾刀刀圈寬度，與刀圈直徑、結構有關，這里取5 mm。

代入相關數據，計算可得刀間距。 為了確定最優刀間距， 分別取刀間距6，8，10 mm 以及12 mm進行滾刀協同破巖仿真，滾刀破巖形成的軌跡如圖2所示。 由圖1 可以看出，不同刀間距下的滾刀協同破巖效果存在明顯的區別，在給定的滾刀、巖石參數以及切深2 mm 的情況下，刀間距8 mm 時的破巖仿真效果較好， 相鄰滾刀之間的破壞區域會相互重合，滿足滾刀協同破巖要求。 同樣地，刀間距6 mm 也可達到了較好的破巖仿真效果，但是刀間距太小會使破壞區域過度重合， 造成破巖能量的浪費。 刀間距10 mm 和12 mm 的破巖效果相對不太理想，隨著刀間距增大，其滾刀之間的巖脊就會越明顯。

圖2 不同刀間距下滾刀協同破巖軌跡Fig.2 Collaborative rock breaking trajectory of disc cutters under different cutter spacing

圖3 為不同刀間距下的滾刀協同破巖的滾動力變化曲線，可以看出，滾刀1 和滾刀2 所受滾動力在整個切削過程中呈現出階段式波動，并且兩滾刀所受滾動力的變化曲線大致上完全相等，但是難以對比在不同刀間距下的滾刀進行協同破巖時所受的滾動力大小以及變化情況。

圖3 不同刀間距下滾刀協同破巖的破巖力變化曲線Fig.3 Variation curves of collaborative rock breaking force of disc cutters for rock breaking under different cutter spacing

為了解不同刀間距的滾刀進行協同破巖時其滾動力變化情況，取滾刀滾動力在不同刀間距下的平均值進行對比，如表1 所示，可以看出不同刀間距下的平均滾動力會有明顯差異，其滾動力并不是隨著刀間距增大而不斷增加，而是在刀間距8 mm 時出現了最低值。 這是因為在合適的刀間距下，滾刀之間協同破巖能使巖石內部產生更多裂紋，從而更容易破碎，那么巖石體對滾刀的反作用力也就減小，而過密的刀間距會導致滾刀之間作用區域重復，對于巖石的巖渣未能有效清除而導致再次作用， 致使刀間距6 mm 比8 mm的滾動力要大，在刀間距超過8 mm 時，其平均滾動力隨刀間距的增大而逐漸增加，說明兩滾刀之間作用區域的裂紋未連接或者連接的裂紋不足以讓兩刀之間巖石破碎形成巖渣，相鄰滾刀之間只能各自形成切割凹槽，從而兩條破巖軌跡之間出現巖脊現象。

表1 不同刀間距下的破巖力平均值Tab.1 Average value of breaking force under different disc cutter spacing

對于滾刀的布置一般呈現螺旋線排列， 考慮到刀盤中心區域需布置中心刀具以及刀盤驅動軸承，刀盤的中心區域直徑定為150 mm，滾刀初始半徑定為80 mm，刀間距為8 mm，相鄰滾刀之間距離是相同的，但是不同輻條的第1 個滾刀距離刀盤中心的距離是不同的，滾刀螺旋線按逆時針布置，則按逆時針第1 個滾刀距離刀盤中心分別為80，88，96，104 mm，每個輻條滾刀相距32 mm，則可知上、下以及左輻條布置5 個滾刀，而右邊輻條布置6 個滾刀。

2.2 整體刀盤結構的切刀設計

切刀作為盾構模型機以及后續模型試驗最重要的刀具之一，也是數量最多的切削刀具，其布置是否合理將直接影響到刀盤的切削效率，對后續模型盾構機的模型試驗精確性起決定性作用。 布置切刀的核心要求在于中心刀與切刀相互配合，其切削軌跡需布滿整個刀盤面，對于本次切刀的安裝主要分布在刀盤開口的兩側，對稱布置，可直接對土體進行切削。 目前來說，布置切刀主要有同心圓布刀法、阿基米德螺旋線布刀方法以及單羅馬螺旋線布刀方法等3 種主流方法[19]。

2.2.1 基于同心圓布刀法設計

采用同心圓布刀方法時， 考慮到刀盤中心區域需布置中心刀具以及刀盤驅動軸承等影響以及考慮到后續拆卸安裝問題， 中心區域直徑定為150 mm，設切刀初始半徑為70 mm， 刀間距為15 mm，切刀刀寬為30 mm，周邊刮刀刀寬25 mm，則通過計算可知，切刀在各輻條的布刀位置距刀盤中心點分別為70，115，160，205，250 mm，其中每個輻條兩側對稱布置，則可知左右的輻條兩側分別布置3 把，位置為70，160，250 mm，而上下的輻條兩側分別布置2 把，位置為115，205 mm，如圖4（a）所示。

2.2.2 基于阿基米德螺旋線布刀法設計

由于刀盤整個空間的有限性，阿基米德螺旋線只采用單螺旋線。 基于阿基米德螺旋線布刀法的計算，則可以得到刀盤正右方輻條的布刀位置距離刀盤中心分別為90，210 mm；正上方輻條的布刀位置距離刀盤中心分別為120，240 mm； 正左方輻條的布刀位置距離刀盤中心分別為150，270 mm； 正下方輻條的布刀位置距離刀盤中心為180 mm， 共7把切刀，本著切刀正反對稱布置原則，即刀盤面板上的切刀數為14 把， 左右分別4 把， 上下分別3把，如圖4（b）所示。

2.2.3 基于單費馬螺旋線布刀法設計

根據單費馬螺旋線在刀盤面板上布置切刀時首先要確定刀盤直徑以及周邊刮刀的布置位置，從而確定切刀數量、刀寬以及布置位置。 基于單費馬螺旋線布刀法的計算，則可以得到刀盤正右方輻條的布刀位置距離刀盤中心分別為100，224 mm；刀盤正上方輻條的布刀位置距離刀盤中心分別為142，245 mm； 正左方輻條的布刀位置距離刀盤中心分別為174，265 mm；正下方輻條的布刀位置距離刀盤中心為200 mm，共7 把切刀，本著切刀正反對稱布置原則， 即刀盤面板上的切刀總數為14 把，其中左右分別4 把，上下分別3 把，如圖4（c）所示。

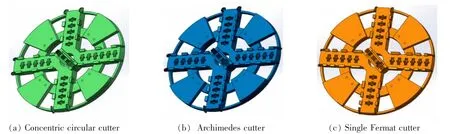
圖4 基于不同布刀方法的刀盤模型Fig.4 Cutterhead model based on different methods of arranging cutters

3 刀盤模型動態仿真分析

3.1 刀盤數值模型建立

為對比上述3 種切刀布置方法的刀盤結構優劣，進行掘削動態仿真分析。 主要比較3 種切刀布置方法的優劣，判斷是否合理；因此在刀盤上暫不布置滾刀，僅考慮布置切刀、周邊刮刀以及中心刀。 通過SolidWorks 軟件對盾構模型機的刀盤進行三維建模，在不影響刀盤整體結構強度的前提下， 可做以下簡化處理：

1） 刪除刀盤面板上所有的螺栓式結構，假定直接連接在刀盤面板上；

2） 刪除滾刀及刀座， 并且僅保留一邊切刀、周邊刮刀以及中心刀；

3） 刪除刀盤的倒角、圓角等復雜部位，便于后續網格劃分。

刀盤的材料采用Q345 鋼，并采用線彈性模型，其中刀盤模型采用C3D8R 單元，單元總數為64 222，土層選用濱海地層的粉質粘土，采用擴展的D-P 模型，其中土體模型同樣采用C3D8R 單元，單元總數為108 425 個。 在刀盤旋轉切削掌子面土體這一動態仿真過程中，引用單元失效準則模擬土體的切削分離過程，從而分別檢驗基于同心圓布刀法、阿基米德螺旋線布刀法和單費馬螺線布刀法的切刀切削軌跡以及結合中心刀、周邊刮刀的切削軌跡能否滿足切削整個掌子面的設計要求。

3.2 基于動態仿真結果的刀具布置優選

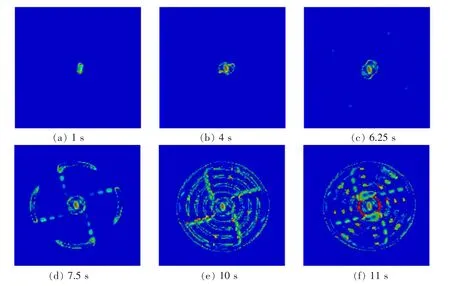
圖6 阿基米德螺旋線不同時刻刀盤切削土體動態圖Fig.6 Dynamic diagram of soil cutting by cutterhead at different time with Archimedean spiral

圖5～圖7 分別為基于同心圓布刀法，阿基米德螺旋線布刀法，單費馬螺旋線布刀法的切刀組合中心刀，周邊刮刀在不同時刻的土體切削動態圖。 其中在0～6.25 s 這一時間段內，都是中心刀具先與土體直接接觸，對中心區域土體進行旋轉切削并產生塑性變形，隨后與待開挖土體分離形成渣土，退出后續模型計算；在6.25～7.5 s 這一時間段內，周邊刮刀開始切削土體并逐漸確定整個待切削面的范圍，由于中心刀具、周邊刮刀布置位置均相同，在0～7.5 s 這一時間段內，3 種布置方法的切削效果表現完全一致；在T=7.5 s 時切刀開始與土體接觸，隨著刀盤繼續推進、旋轉，此時待切削面的土體被分成四部分先后切削，切削后的土體會逐漸重合；在T=10 s 時，刀盤旋轉切削一圈，此時開挖面土體已被全面切削， 而當T=11 s 時已進入下一個循環周期。 從土體的切削分離狀態來看，可以發現阿基米德螺線和單費馬螺線的刀具布置方法均能實現土體的全面切削，同心圓布置法存在切刀之間不完全切削現象，不滿足使用要求。

圖5 同心圓布置法不同時刻刀盤切削土體動態圖Fig.5 Dynamic diagram of soil cutting by cutterhead at different time with concentric circle arrangement method

圖7 單費馬螺線不同時刻刀盤切削土體動態圖Fig.7 Dynamic diagram of soil cutting by cutterhead at different time with single Fermat spiral

在整個刀盤旋轉切削的數值仿真中，可知只對比待開挖面土體的切削分離狀態是無法甄別最優布刀方法的， 而對于在整個切削過程中刀盤荷載隨著時間的變化規律也是一個重要考量因素。3 種布刀方法的刀盤結構在整個動態仿真過程中所受荷載隨時間的變化曲線如圖8， 圖9 所示。

圖8 不同結構刀盤隨時間對應刀盤推力曲線圖Fig.8 Curves of cutterhead thrusts of different structure cutterheads over time

從圖8，圖9 中均可以看出，在0～6.25 s 的這一時間段內，只有中心刀具在對中心區域的土體進行旋轉切削，刀盤的推力、扭矩隨著中心刀具不斷深入而緩慢增加；在6.25～7.5 s 這一時間段內，周邊刮刀開始進行切削工作，逐漸形成整個刀盤的掌子面切削范圍，此階段內的中心刀具以及周邊刮刀進行旋轉切削，刀盤的推力、扭矩會有一定的明顯上升趨勢；在7.5～10 s 這一時間段內，這時刀盤面板上數量最多的切刀開始與土體接觸，此階段刀盤上切刀、中心刀以及周邊刮刀都對整個待切削面進行旋轉切削，在這一時間段內的刀盤推力、扭矩開始陡然上升；在10 s 后，刀盤完成旋轉切削一圈，刀盤的推力、扭矩均已達到最大值，此時所有的刀具都全部進入切削工作，由于采用了土體損傷失效分離準則，隨著刀盤的推進、旋轉，不斷有已失效的土體退出計算以及切削新的待切削土體，從而使得刀盤的推力、扭矩開始處于上下波動的穩定狀態，其變化趨勢符合實際要求。

圖9 不同結構刀盤隨時間對應刀盤扭矩曲線圖Fig.9 Curves of cutterhead torques of different structure cutterheads over time

將同心圓布刀法、阿基米德螺旋線布刀法以及單費馬螺旋線布刀法得到的刀盤結構所受推力和扭矩進行匯總，如表2 所示。 根據理論計算得到的刀盤推力、扭矩值以及對比表2 可知，因為在動態切削仿真過程中未考慮到土層地應力以及埋深的影響，其仿真結果都比理論計算值要小。 其中單費馬式的刀盤得到的最大以及平均推力、扭矩相對阿基米德式、同心圓式的刀盤均要小，說明單費馬螺旋線布刀方法要優于另兩種，能有效減少刀盤所受荷載。 本著刀盤整體受力情況最好的設計原則，選用單費馬螺旋線布刀法在刀盤面板上布置相應的切刀。

表2 不同布刀類型的刀盤荷載情況Tab.2 Load situation of cutterheads of different layout types

4 刀盤結構受力性狀分析

由圖10（a）～圖10（c）可以看出，正常推進工況下的刀盤最大應力為61.03 MPa， 最大推力工況下的刀盤最大應力為118.7 MPa， 以及最大扭矩工況下的刀盤最大應力為18.53 MPa，都小于Q345 材料的許用應力；由圖10（d）～圖10（f）可以看出，正常推進工況、最大推力工況以及最大扭矩工況下的刀盤最大位移量分別為0.36，0.228 mm 和0.617 mm，位移量都比較小，刀盤結構幾乎沒有變形。 綜合考慮盾構模型機的刀盤在動載荷下的載荷分析和靜載荷下的應力應變分析，基于單費馬螺旋線布刀法的刀盤滿足全面開挖掌子面土體的要求，以及其整體強度、剛度均能夠滿足一般機械使用要求，刀盤大部分區域應力均相對較小，只有極小部分區域應力相對較大，但都小于材料的許用應力，并且各個工況下刀盤變形均相對較小，幾乎可忽略不計，可直接進行生產加工制作實物。

圖10 3 種工況下刀盤應力應變圖Fig.10 Stress and strain diagram of cutterhead under three working conditions

5 結論

本文針對濱海復合地層的地質特征，對微型盾構機刀盤進行了優化設計。 主要結論如下：

1） 雙滾刀協同破巖仿真過程中，滾動力并不是隨著刀間距增大而不斷增加， 在刀間距8 mm 時出現最低值，表明在合適的刀間距情況下，滾刀協同破巖會導致巖石內部產生更多裂紋，從而更容易破碎，可提高破巖效率。

2） 基于阿基米德螺線和單費馬螺線布刀法的刀盤均能滿足掌子面全開挖的要求，同心圓布刀法刀盤切刀之間存在不完全切削現象；3 種刀盤結構的動態仿真過程中，0～7.25 s 階段主要由中心刀和周邊刮刀切削土體，推力、扭矩變化曲線基本一致，7.25 s 以后切刀開始和土體接觸， 土體被分成四部分先后切削，切削后的土體會逐漸重合并形成同心圓，推力、扭矩均急劇上升，10 s 以后刀盤完成旋轉一圈，推力、扭矩均達到最大值；最終根據刀盤整體切削效果以及推力、扭矩大小，確定單費馬螺旋線布刀法為最優布刀方案。

3） 考慮微型盾構機掘進的正常工況、最大推力工況以及最大扭矩脫困工況，針對單費馬螺旋線布刀法的刀盤結構強度與剛度進行驗算，結果表明其應力強度均滿足要求，變形位移分別為0.36，0.228，0.617 mm，滿足一般工程機械使用要求。