數理統計在混凝土輸水管脫模強度控制中的應用
張瑞國 亓文菁 喬 楨 李建群 王恒一
(泰安市質量技術檢驗檢測研究院,山東 泰安 271000)
混凝土輸水管是用于調水、引水工程、城市給水系統、排水系統、工業和水利輸水管線、工廠管網、電廠補給水管及冷卻水循環系統、雨水、污水及農田排灌等輸送水介質用的管材,產品主要包括自應力混凝土管、預應力混凝土管、預應力鋼筒混凝土管和鋼筋混凝土排水管等。
眾所周知,混凝土強度是混凝土制品的重要指標之一,從混凝土強度表達式可以看出,混凝土抗壓強度與混凝土用水泥強度成正比,按公式計算,當水灰比相等時,高標號水泥比低標號水泥配制出的混凝土抗壓強度要高許多。影響混凝土抗壓強度的主要因素也有很多,與水泥強度、水灰比、粗細骨料、外加劑的種類、摻入量、摻入方式有著密切聯系。混凝土強度只有在溫度、濕度適宜條件下按照施工規范規定予以養護,脫模,才能保證強度的正常發展。要想滿足產品最短周期的連續性模具生產,脫模強度又成了工序質量優劣、產品質量好壞的主要標志和因素。國家標準對混凝土制品脫模強度的要求是必須達到設計強度的70%。有些企業產品的力學性能檢驗雖然能達到基本的設計要求,但由于在脫模和吊運過程中,外觀破損造成一次性合格率低,這些企業也做了不少混凝土強度試塊,但總是處于盲目的事后檢查狀態。至于混凝土的脫模抗壓強度存在哪些問題,實際應控制在多少標號,相關人員并未做過分析,也沒有一個具體的控制范圍。因此,我們對此進行了統計分析,闡述如下,以供大家參考。
1 統計分析與理論控制
為了能找出問題,我們從三階段預應力壓力管C40混凝土著手,從近幾年的混凝土脫模強度試塊原始記錄中做了統計調查,無規律隨機抽取100個數據結果(見表1),進行了數理統計分析(見表2),求出了實際脫模強度的均值μ,標準偏差σ和變異系數CV。
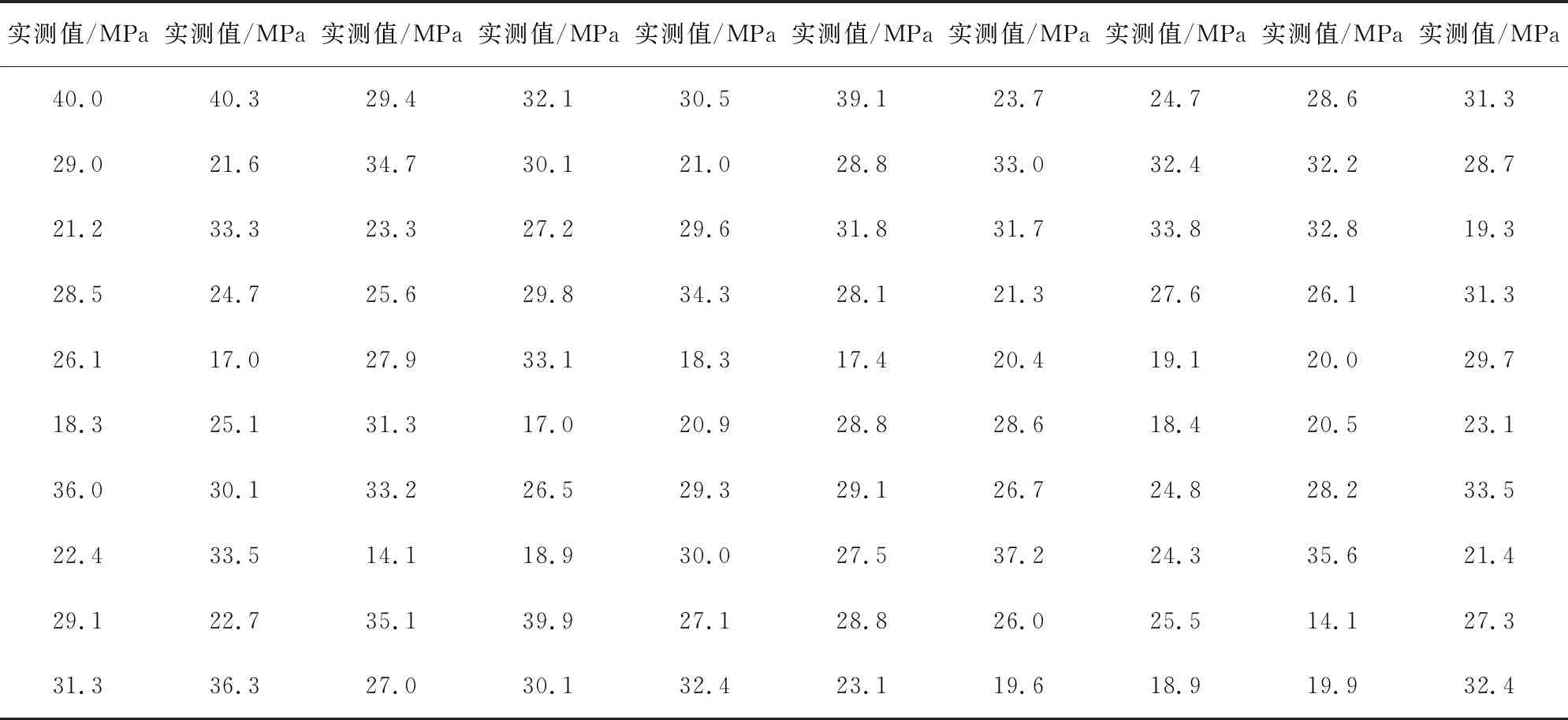
表1 砼脫模強度試塊實測值

表2 數理統計分析
Xmax=40.3,Xmin=14.1,組數K=12,




(其中29.5為Ui=0時的Xi值
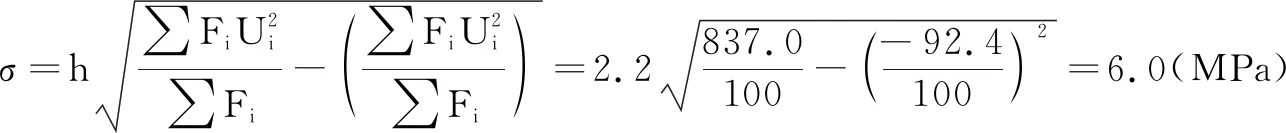

由統計分析對這些混凝土脫模強度可做如下結論。
1.脫模抗壓強度值這一隨機變量的分布接近于X~N(μ,σ)的正態分布。
2.均值μ=27.5MPa,強度值的分布中心達不到標準要求的最低下限(28MPa)。
3.標準偏差σ=6.0,變異系數Cv=21.8%,強度值的離散性過大。
如果按于X~N(μ,σ),正態分布情況求其混凝土脫模強度合格品的概率,由分布函數公式得:
1-φ(0.083)=1-0.53=0.47
通過以上計算可知,滿足脫模強度不得低于28MPa標準要求的合格品僅占47%,因此可以斷定造成產品在脫模、吊運過程中外觀破損、修補量大、一次性合格率低的主要原因是混凝土脫模強度值偏低,而且強度值的離散性、波動性偏大。工序不處于一種正常的穩定狀態,故此也不能以現狀的統計數值為依據進行質量控制。另外,因為正態分布X~N(μ,σ)的概率是由均值μ和方差σ兩個參數決定的,可以從數學角度考慮,要想減少破損,提高產品的合格率,關鍵在于需提高均值μ和降低方差σ值。那么,究竟均值μ和方差σ兩參數應控制在多少,下文通過公式進行求證。
假定求得的實際值均加上一個實際標準偏差27.5MPa+6.0MPa=33.5MPa作為均值, 以實際均值27.5MPa為下限,則上限應為33.5MPa+6.0MPa=39.5MPa,在要求產品的合格率大于92%的情況下,如不考慮其他因素,而只考慮脫模強度一項引起產品缺陷的前提下,在其控制區間的概率應達到和超過0.92,即:P(27.5 P(27.5 把②代入①得: 反查標準正態分布表得 如果按假定的均值33.5MPa作為控制均值, 那么就應當在現有情況下把強度值提高6.0MPa, 那么, 即便企業條件得以實現, 富裕強度出現的幾率也會隨之增加,對施工造成過多浪費, 經濟成本上也是不允許的, 所以必須對假定情況做進一步修正。 可在脫模強度的標準要求基礎上加上一個計算方差作為控制均值μ=28.0MPa+3.4MPa=31.4MPa, 然后將上下限定為μ±2σμ±2σ,即: LCL=μ-2σ=31.4-2×3.4=24.6 MPa(下限) UCL=μ+2σ=31.4+2×3.4=38.2 MPa(上限) 因為控制區間是在μ±2σ范圍內,所以由正態隨機變量的三個重要數據,不必計算便可知道P(μ-2σ P(X≥28)=-2σ 在混凝土輸水管的生產過程控制中,引入數理統計的方法,能比較準確的反映整批混凝土某一時間點的強度水平,混凝土脫模強度將會穩定上升,從而為下一道工序的展開提供科學依據,產品一次性合格率將有更大改觀,盡最大可能提高生產效率,降低生產成本。
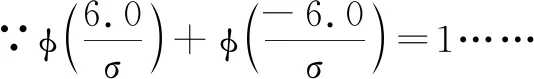
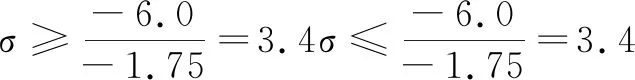
2 結 論

