干濕循環作用下陜北Q2黃土強度及水土特性試驗研究

白偉， 魏進， 卞海丁， 黃璜

(1.延安萬凱交通工程有限責任公司， 延安 716099; 2.長安大學公路學院， 西安 710064)

黃土主要分布于干旱與半干旱地區，具有良好的非飽和工程特性，因此黃土高原是中國地質災害的頻發地區，水土流失極為嚴重[1]。黃土邊坡在自然條件下處于蒸發-降雨的無限循環中，反復的蒸發-循環效應會導致土顆粒骨架損傷，從而造成坡體強度與土水特性發生變化[2-3]，甚至發生滑動，這將導致巨大的安全隱患。

基于此，巖土界學者在干濕循環作用下黃土的強度及土水特征曲線等方面做了大量研究。劉宏泰等[4]針對重塑黃土在干濕循環作用下的滲透性與強度問題進行了研究；袁志輝等[5]利用常規三軸試驗發現黃土的結構與衰減強度皆伴隨其含水率增大而降低，呈較好的對數函數關系，且試驗證明了原狀黃土在經反復多次干濕循環后與重塑黃土結構基本相同；王飛等[6]通過對壓實黃土路基土在反復干濕循環作用下的變形特性進行分析，發現割線模量與反復干濕循環次數之間呈負相關指數函數關系，與初始壓實度呈正相關指數函數關系；劉奉銀等[7]對黃土干濕循環作用下的土水特征曲線的滯回特性規律進行了初步的研究探討；趙天宇等[8]認為密度對黃土土水特征曲線的影響明顯，VG(Van Genuhten)模型可對非飽和黃土土水特征曲線進行很好的預測與描述；孫志杰等[9]通過模型試驗研究發現，干濕循環次數與幅度均會對黃土邊坡坡面造成較為嚴重的影響；王鐵行等[10]認為結構強化與動強度提升的主要影響因素是孔隙結構向均勻小孔隙演化和基質吸力使土樣趨于密實；Chou等[11]認為Gardner模型更適合描述土-水特征曲線，通過Gardner模型和Childs&Collis-George模型實測的土-水特征曲線分別得到了與基質吸力呈指數關系、與體積含水量呈冪函數關系的非飽和黃土滲透系數預測模型；潘振興等[12]研究表明，隨著干濕循環次數的增加，因黃土內部顆粒的集散動態變化致使黃土損傷，故土體呈塑性指數及液限減小、孔隙率增大、塑限基本不變的規律。

綜上可知，學者們針對黃土在干濕循環作用下強度衰減機理、物理力學性質及結構特性研究頗多，但對黃土抗剪強度與土水特征曲線在不同干濕循環次數下的衰減預測研究較少。基于此，現以陜西延安Q2黃土為研究對象，通過直剪試驗、濾紙法探究Q2黃土土水特性與抗剪強度的干濕循環效應，希望能為黃土高原地區黃土滑坡災害防災減災提供理論參考。

1 干濕循環試驗研究

1.1 土樣物理力學指標

試驗土樣取自延安市南泥灣樊莊邊坡坡體中下部3 m處，為陜北Q2黃土，原狀土與重塑土各取一部分，共取16個原狀樣。其中原狀土采用聚氯乙烯(PVC)管裝樣，PVC管直徑110 mm，高250 mm，裝樣后兩端用保鮮膜包裹，并用膠帶纏緊，最后刷一層蠟密封好。現場取樣如圖1所示。

根據《公路土工試驗規程》(JTG 3430—2020)[13]，分別采用環刀法、烘干法、比重瓶法、液塑限聯合測定法對黃土的基本物理力學性質指標進行了測試，土工試驗結果如表1所示。

圖1 現場取樣Fig.1 Field sampling

表1 陜北Q2黃土基本物理力學性質指標

1.2 試驗原理

1.2.1 土-水特征曲線理論

土-水特征曲線(soil-water characteristic curve，SWCC)反映了非飽和土中體積含水量隨基質吸力的變化衰減規律。圖2為典型SWCC的示意圖，可以看出，體積含水量隨著基質吸力的增大先保持不變，再急劇減小，最后趨于穩定。曲線上第一個反彎點M1對應的橫坐標表示土的進氣值，其含義為當土中孔隙氣壓力增大到一定程度時，使土體孔隙開始排水，此時的基質吸力稱為進氣值，用(ua-uw)b表示；曲線上第二個反彎點M2對應的橫坐標表示土的殘余吸力，其對應的縱坐標表示殘余體積含水量。

圖2 典型土-水特征曲線示意圖Fig.2 Schematic diagram of typical soil-water characteristic curve

1.2.2 非飽和抗剪強度理論

Fredlund非飽和抗剪強度公式為

τf=c′+(σ-ua)tanφ′+(ua-uw)tanφb

(1)

式(1)中：τf為非飽和抗剪強度；σ為法向應力；ua為孔隙氣壓力；uw為孔隙水壓力；φb為隨基質吸力變化的內摩擦角。

由式(1)可知，τf由有效黏聚力c′、有效內摩擦力(σ-ua)tanφ′以及與基質吸力相關的吸附強度(ua-uw)tanφb組成。當土體含水率發生改變時，根據土-水特征曲線的定義，式(1)右邊第三項中的基質吸力(ua-uw)與體積含水量θ呈函數關系。

相關研究表明[14-15]，不同含水率下土樣的內摩擦角幾乎是不變的，而黏聚力隨含水率的變化有明顯的改變。因此，可將式(1)右邊第一項和第三項合并為一項，稱為表觀黏聚力c，即

c=c′+(ua-uw)tanφb

(2)

式(2)中：(ua-uw)可根據土-水特征曲線確定，代入式(2)即可得到不同含水率土體的抗剪強度參數c′、φb。

1.3 試驗方案

1.3.1 土-水特征曲線實驗方案

降雨-蒸發實際上是一個干濕循環的過程。試驗采用真空飽和器飽和土樣，模擬土體降雨增濕的過程，設置烘箱溫度為40 ℃，模擬太陽照射下土體蒸發脫濕的過程。通過將原狀土樣進行不同的干濕循環次數，測定其土-水特征曲線并進行分析，研究陜北Q2黃土土-水特性隨干濕循環次數的變化規律。

同時根據相關研究[16-17]，經3次干濕循環后，土體的持水性能逐漸呈現穩定趨勢。因此，試驗設定土樣的干濕循環次數分別為1、2、3、5。將經過干濕循環后的土樣制成環刀樣，烘干，每兩個環刀樣一組，采用滴定法將各組環刀樣配制成不同的質量含水率，然后用濾紙法測定Q2黃土的土-水特征曲線，試驗方案設計如表2所示。

表2 土-水特征曲線試驗方案

1.3.2 非飽和抗剪強度實驗方案

為研究不同的干濕循環次數對原狀非飽和黃土的抗剪強度特性的影響，試驗采用慢剪法并結合土水特征曲線試驗結果，研究不同干濕循環條件下陜北Q2黃土的抗剪強度變化規律。試驗方案設計如表3所示。

表3 非飽和抗剪強度試驗方案

2 試驗結果分析

2.1 不同干濕循環次數下Q2黃土的土-水特征曲線分析

圖3為不同干濕循環次數下陜北Q2黃土脫濕與增濕的土-水特征曲線，總體而言，不同干濕循環次數下土-水特征曲線呈現出的變化趨勢大體相同。

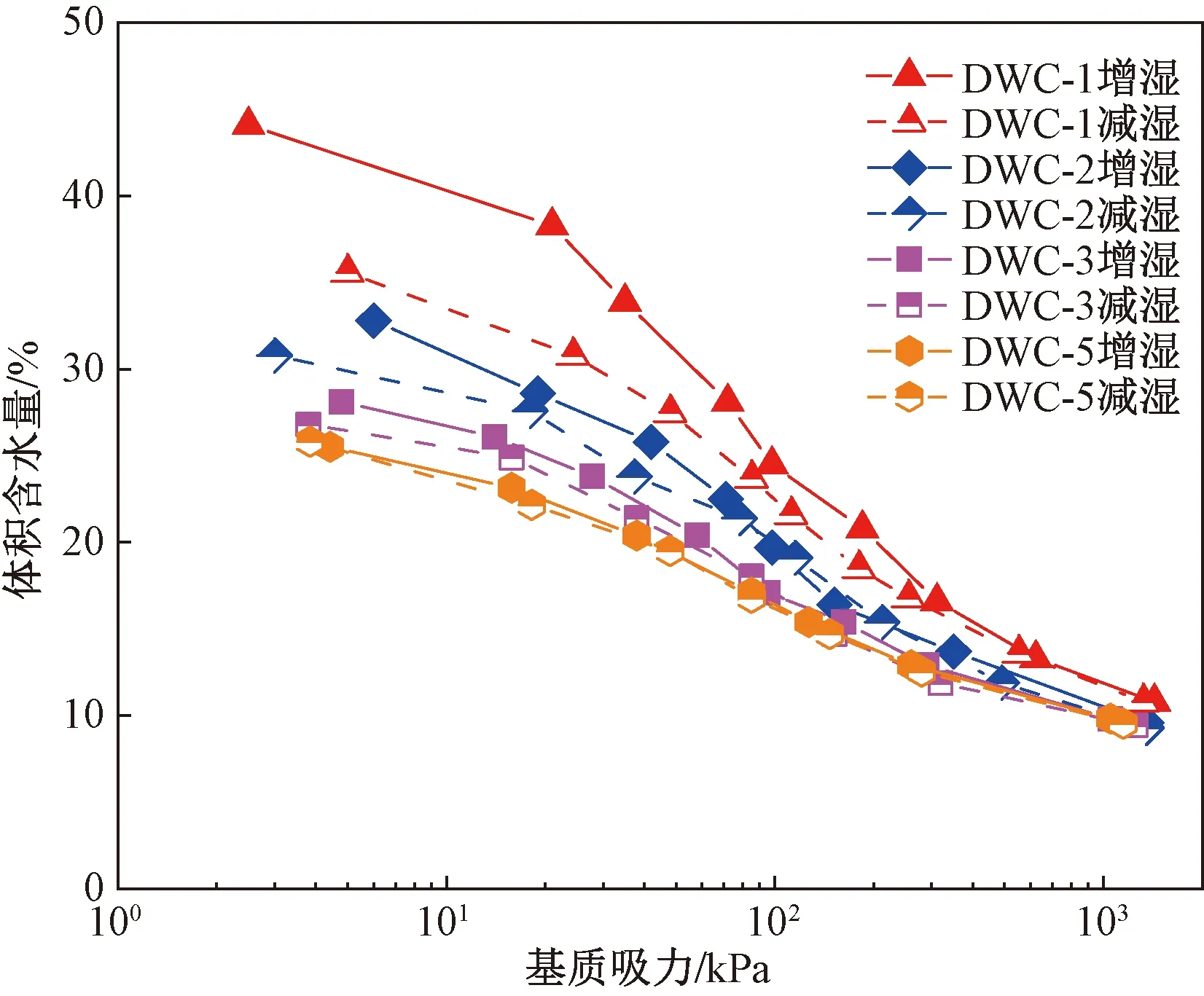
圖3 不同干濕循環次數下的土-水特征曲線Fig.3 Soil-water characteristic curve under different drying-wetting cycles

同時由圖3可知：土體經脫濕后，在吸濕過程中由于土體孔隙大小差異，孔隙水涌入后會產生“瓶頸效應”，導致吸濕后的體積含水量小于脫濕時的體積含水量，因此，脫濕曲線與吸濕曲線之間由于高度差會形成滯回圈，同一干濕循環次數下脫濕曲線始終位于增濕曲線的上方。

第五次脫濕曲線的斜率明顯小于第一次脫濕曲線的斜率，這是由于第一次脫濕時土體孔隙比較大，持水能力很弱，因此脫濕速率較快，隨著干濕循環次數的增多，土體體積不斷發生變化，其內部骨架結構也在逐漸發生重分布，導致孔隙比逐漸減小，持水能力持續加強，因此脫濕速率會隨著干濕循環次數的增多而持續減小，由表4可知，第二次脫濕時的脫濕速率降幅最明顯，相比較第一次脫濕下降約30%。

隨著干濕循環次數的增加，脫濕曲線第一個拐點M1的位置逐漸向左移動，進氣值逐漸降低，且下降幅度逐漸減小，第二次脫濕時的進氣值約為第一次的2/3。其原因是在反復干濕循環條件下，土體體積含水量不斷減小，土體骨架結構不斷收縮，但同時造成土體內部分中、小孔隙向深部擴展逐漸形成大孔隙，因此，第一次脫濕時進氣值最大，隨著干濕循環次數的增加，進氣值不斷減小直至趨于穩定。

在反復干濕循環條件下，土骨架不斷收縮造成

表4 最大脫濕速率與進氣值隨干濕循環次數變化

土體飽和體積含水量不斷減小，由圖3可以看出，每次干濕循環時脫濕曲線與吸濕曲線都會產生高度差，且第一次干濕循環時產生的高度差最大，第五次干濕循環時脫濕曲線與吸濕曲線近似重合，高度差已經不明顯，因此，每次干濕循環由于均能產生滯回效應，隨著干濕循環次數的增加，土樣的持水能力逐漸增強，脫濕曲線與吸濕曲線逐漸逼近，滯回效應逐漸減弱，土體內小孔隙以及孔隙內殘余的氣泡量趨于穩定。

2.2 土-水特征曲線的擬合分析

分別采用Van Genuhten(VG)模型、Brooks-Corey(BC)模型及Fredlund-Xing(FX)模型對試驗結果進行擬合對比，分析3種模型對陜北Q2原狀黃土的適用性。3種模型的表達式如式(3)～式(5)所示，擬合結果如圖4所示。

(1) VG模型。

(3)

(2) BC模型。

(4)

(3)FX模型。

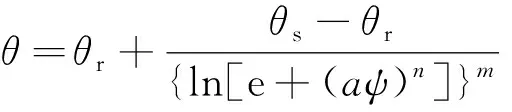
(5)

式中：θ為體積含水量；θs為飽和體積含水量；θr為殘余體積含水量；ψa為進氣值；ψ為基質吸力；m、n為擬合參數，m=1-1/n；a為與進氣值有關的參數；e為自然對數常量。

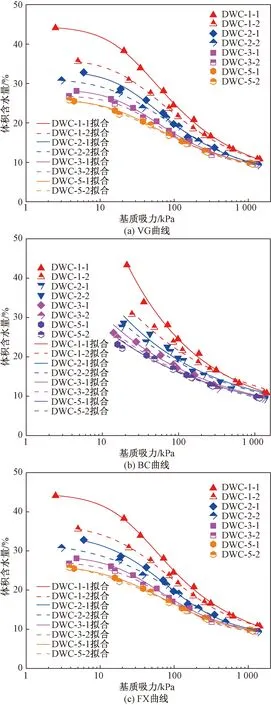
圖4 土-水特征曲線擬合情況Fig.4 Fitting of soil-water characteristic curve

2.3 不同干濕循環次數下土-水特征曲線的預測模型分析

自然界中的邊坡處于長期反復的降雨-蒸發循環中，對于黃土邊坡，測定其多次干濕循環下的土水特征曲線是一項費時費力的工作，為此以VG模型的擬合數據作為基礎，分析土-水特征曲線各項基本參數隨干濕循環次數的變化規律，通過擬合得到不同干濕循環次數下的VG模型預測公式，如圖5所示。

由圖5可知，隨著干濕循環次數的增加，土樣的土水特征參數θs、θr、與進氣值有關的參數a先逐漸減小然后趨于穩定，而土性參數n隨干濕循環的次數增加先逐漸增加然后趨于穩定，相比θs、θr的干濕循環效應不明顯；在第5次干濕循環時，4種基本參數的變化曲線斜率已經基本與x軸平行，因此，可以認為5次干濕循環條件下土-水特征曲線的干濕循環效應基本消失。

采用指數函數可以很好地對VG模型各項基本參數隨干濕循環次數的變化曲線進行擬合，擬合結果如表5所示。

聯立表5中各參數擬合公式與式(3)，即可得到該土樣任意干濕循環次數下VG模型脫濕過程與吸濕過程的SWCC。為了檢驗預測模型的精度，用本文模型計算第4次干濕循環的SWCC，并與試驗數據進行對比，結果如表6及圖6所示。

用預測模型計算的第4次干濕循環脫濕與吸濕曲線與試驗數據點擬合度分別為0.996、0.994，吻合度較高，從而證明了本文模型具有較好的適用性。

2.4 剪應力-剪切位移曲線分析

4組不同干濕循環次數下的固結慢剪試驗結果如圖7～圖10所示，取剪切位移為4 mm時對應的剪應力作為每組試樣的抗剪強度。

圖5 干濕循環次數對VG模型基本參數的影響Fig.5 The influence of the number of drying-wetting cycles on the basic parameters of the VG model

表5 VG模型參數隨干濕循環次數變化擬合公式

表6 第4次干濕循環預測模型與試驗數據對比

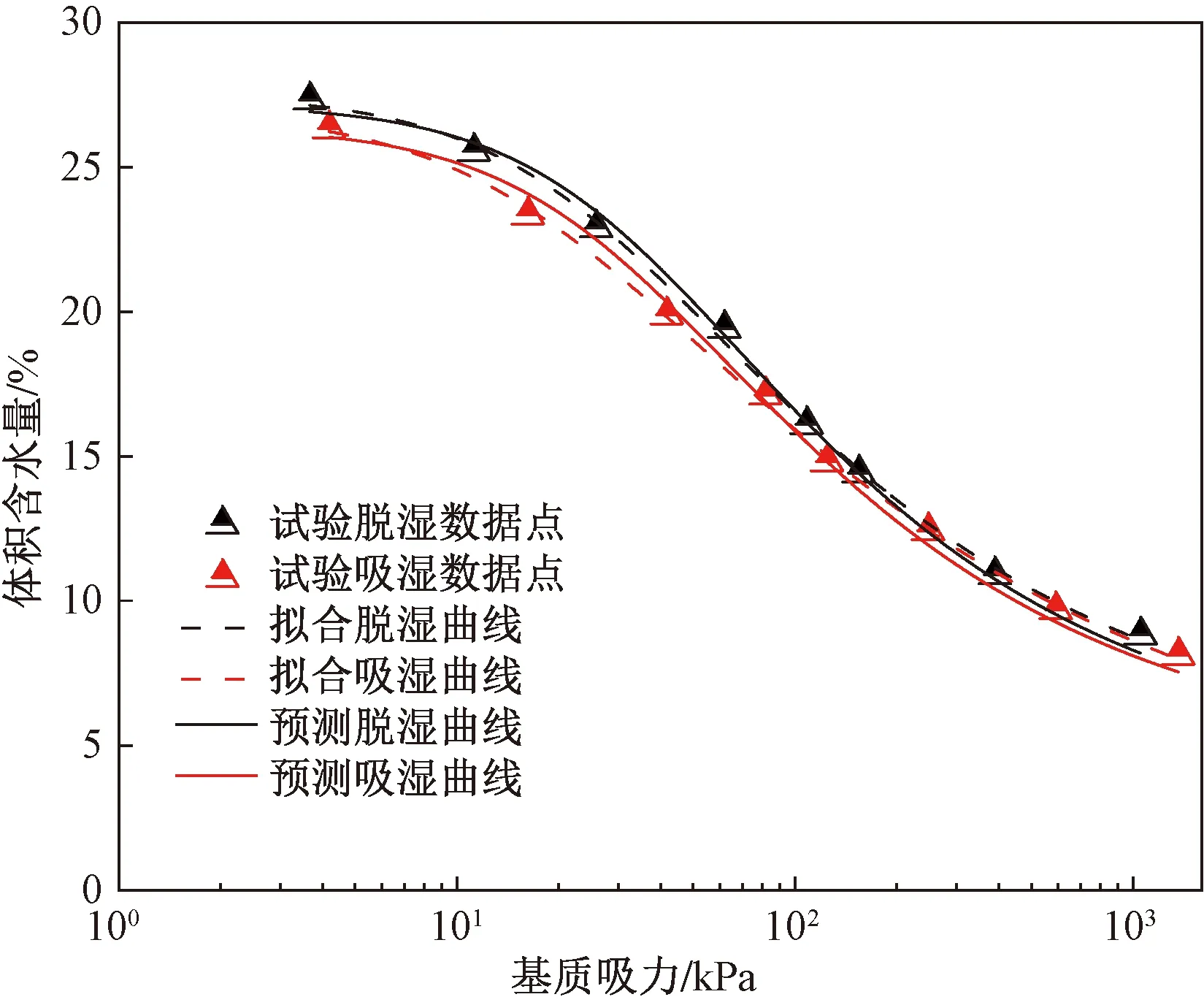
圖6 第4次干濕循環試驗數據擬合曲線與預測曲線對比Fig.6 Comparison of fitting curve and prediction curve of the 4th drying-wetting cycles test data

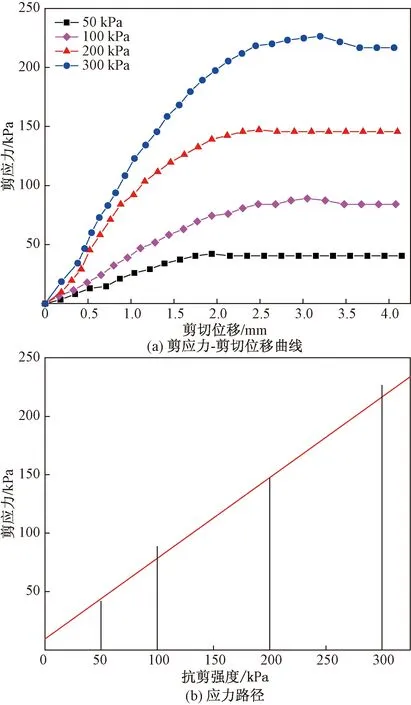
圖7 第1次干濕循環Fig.7 The first drying-wetting cycles

圖8 第2次干濕循環Fig.8 The 2nd drying-wetting cycles

由圖7～圖10可得出如下結論。

(1)隨著干濕循環次數的增加，土樣的剪應力-剪切位移曲線的峰值越發明顯，應變軟化特性逐漸增強，這可能是因為土樣在反復的吸濕-脫濕過程中微觀結構發生了變化，土體內產生了微小裂隙，剪切時沿著剪切面周圍分布的微小裂隙促成了破壞面的形成。

(2)隨著干濕循環次數的增加，土樣達到相同剪切位移時所需的剪應力逐漸減小，土樣的抗剪強度也逐漸減小。

2.5 干濕循環條件下非飽和原狀黃土抗剪強度參數分析

為預測不同干濕循環次數下土樣的抗剪強度，分別通過試驗做出不同干濕循環次數下土樣抗剪強度參數的變化曲線，并對其進行擬合，結果如圖11所示。

由圖11可知，反復的干濕循環可較顯著地削弱土樣的抗剪強度，隨著干濕循環次數的增加，非飽和強度參數φ′、c′及φb均有所降低，強度降低是土微觀結構發生變化的宏觀反映。曲線擬合公式如表7所示。

根據擬合結果可知，非飽和抗剪強度參數均與干濕循環次數成指數函數關系，擬合度較高。由指數函數變化特征可知，隨著干濕循環次數的增加，抗剪強度參數減小的速率逐漸降低，其中第1次干

圖9 第3次干濕循環Fig.9 The 3rd drying-wetting cycles

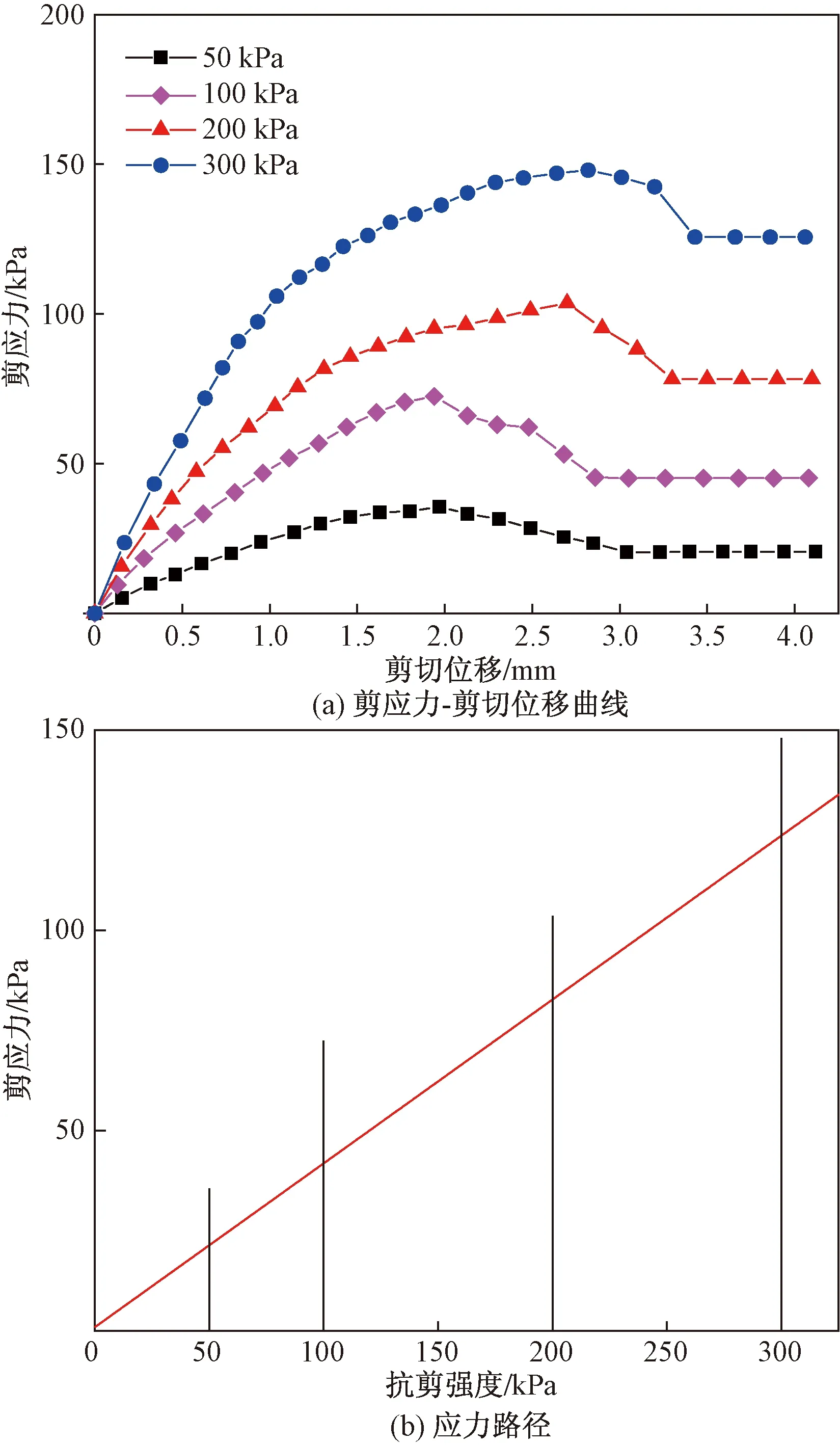
圖10 第5次干濕循環Fig.10 The 5th drying-wetting cycles

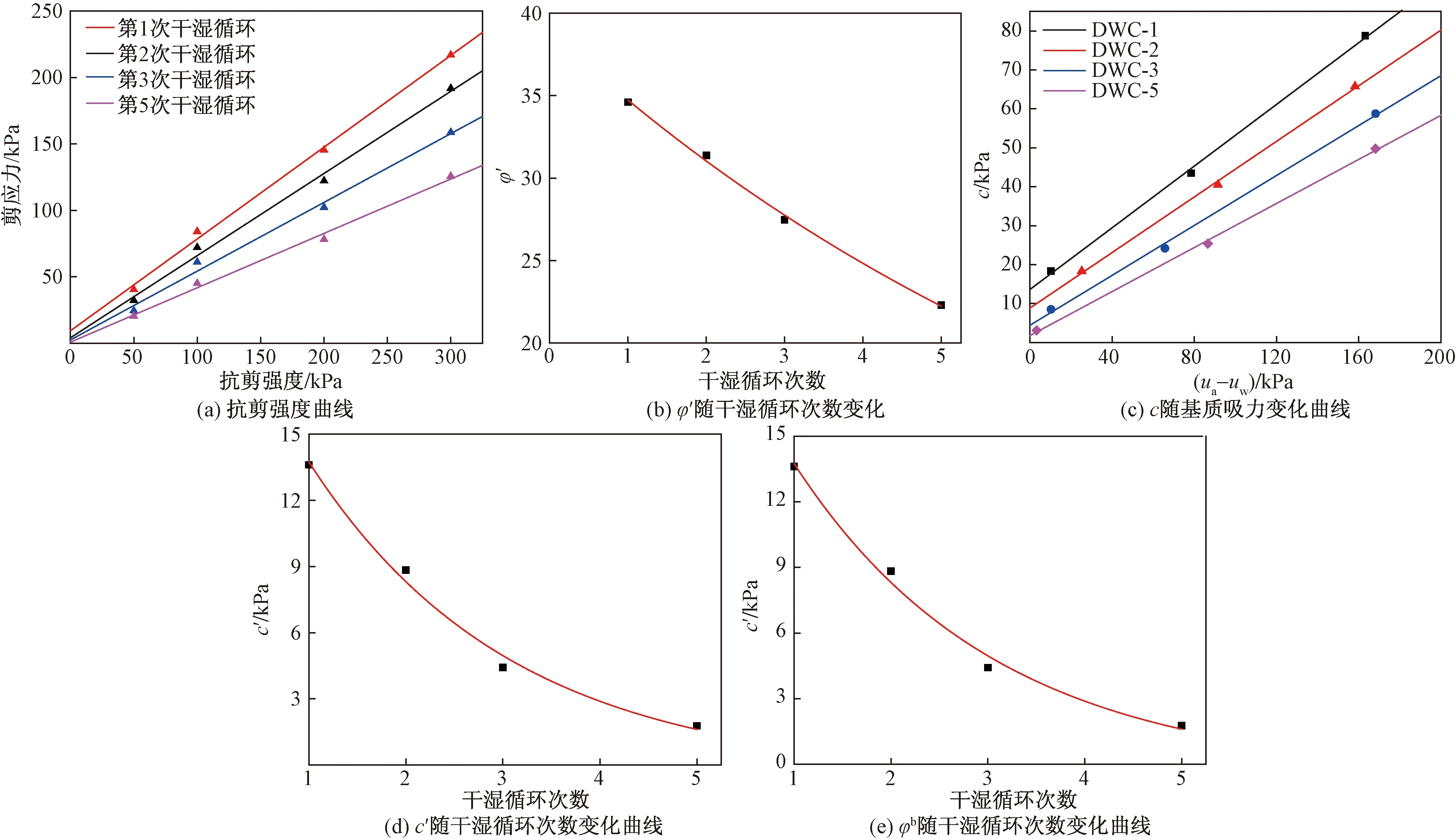
圖11 原狀黃土抗剪強度參數隨干濕循環變化規律Fig.11 Variation of shear strength parameters of undisturbed loess with drying-wetting cycles

表7 非飽和抗剪強度參數隨干濕循環次數變化擬合公式

濕循環時各參數減幅最大，φ′值減小10.3%，c′減小21.8%，φb減小14.4%。

3 結論

主要通過直剪試驗及濾紙法探究了陜北Q2黃土在不同干濕循環次數下其土水特性及強度的變化規律，得出的結論主要如下。

(1)隨著干濕循環次數的增加，黃土的進氣值逐漸降低，且降低的速率逐漸減小，第2次脫濕時進氣值較第1次約降低1/3。

(2)隨著干濕循環次數的增加，黃土脫濕曲線斜率逐漸變緩，持水能力逐漸加強，脫濕速率逐漸減小，第2次脫濕的最大速率比第1次脫濕約降低30%。

(3)隨著干濕循環次數的增加，土樣的抗剪強度應變軟化特性更加明顯，達到相同剪切位移時所需的剪應力越來越小。

(4)得到了土樣的非飽和抗剪強度參數及土水特征曲線參數隨干濕循環次數變化的擬合公式，并預測了第4次干濕循環次數下土樣的土水特征參數，結果表明預測效果較為精確。