基于復雜外力與數據驅動的樹木運動學模型構建

于 舜， 夏 炎， 姜 柳， 王洪江

(沈陽工程學院 信息學院， 沈陽 110136)

樹木造型在當今社會各行業中廣泛使用，尤其在農業農事、動畫視頻、教學場景等行業對逼真樹木模型有著較高的需求，因此，建立基于自然界中復雜外力下真實的樹木模型是當今的研究熱點，同時也是積極拓寬樹木模型使用領域的關鍵[1-4].本文針對在自然環境中，建立能夠模擬出風、雨等復雜外力作用下的樹木動態模型為研究內容，構造真實樹木擺動、斷裂等姿態的動態模型算法.

國內外學術界、產業界有很多關于樹木模型的研究[5-10]，如經典的分形L-system算法等，但是分形算法主要利用迭代、遞歸等技術來實現某一具體的分形構造.由于采用自相似性構造出的樹木模型缺少真實感，與自然界中的樹木有很大的差距，并且分形算法構造出的樹木模型多是靜態模型，難以反映出樹木在自然界中遭遇風、雨等多種因素作用后的動態姿態[11-12].

本文采用在靜態模型的基礎上構建動態模型的方法來搭建樹木整體模型[13]，主要研究斷裂分支的運動軌跡以及與其他樹枝、葉片的碰撞、擠壓作用，建立算法以描繪其碰撞過程.

1 樹木碰撞描述

自然界中的樹木各分支對象，如樹枝、葉片和果實等，受到外力后均有從樹木主干部分斷裂的可能.斷裂后，葉片由于質量較小，在下落過程中對于其他對象產生的影響很小，葉片的撞擊力可以忽略不計，只需考慮風、雨等外力的影響即可.而樹枝和果實的質量不可忽略，所以在其運動過程中，不但要考慮外力的作用，還要考慮斷裂對象的自身重力.外力的組成較為復雜，在自然環境中外力存在于整個空間且包裹作用于樹木對象，對斷裂對象的運動軌跡產生一定影響.本文以風力作為外力的典型代表，結合樹木各分支對象的自身重力和斷裂極限來建立樹木動態模型[14-15].

在整個碰撞過程中，斷裂下落的樹枝(簡稱broken_branch_A)和其他樹枝(簡稱branch_B)的形體不定，但是二者在發生碰撞時的接觸點即碰撞點是一定的，因此在建模過程中，將broken_branch_A和branch_B的接觸點視為球體進行討論[16].本文以在自然界外力作用下樹木各部分對象間的碰撞、擠壓為研究對象建立動態模型.

2 碰撞模型算法分析

結合broken_branch_A和branch_B二者發生碰撞的實際情況，可以將斷裂下落的broken_branch_A和branch_B的碰撞分為正向碰撞和側向碰撞.二者發生碰撞時的速度與二者球心的連線在同一條直線上，且碰撞后二者的速度仍會沿著這條直線，則視為正向碰撞；二者發生碰撞時的速度與二者球心的連線不在同一條直線上，且碰撞后二者的速度都會偏離這條直線，則視為側向碰撞.

設broken_branch_A和branch_B的質量為MbbA和MbB，半徑為RbbA和RbB，楊氏模量為EbbA和EbB，泊松比為μbbA和μbB.broken_branch_A與branch_B發生碰撞后，將撞擊力與branch_B的斷裂極限值比較可得：撞擊力高于斷裂極限值時，branch_B發生斷裂；反之branch_B不發生斷裂，只在外力作用下進行擺動.

2.1 broken_branch_A和branch_B的正向碰撞

2.1.1 broken_branch_A垂直方向與branch_B發生正向碰撞

在發生碰撞的整個過程中，隨著broken_branch_A和branch_B間的撞擊面積增大以及接觸時長的增加，撞擊力IMPACT_F也逐漸增加到最大值，branch_B受到碰撞后的狀態由IMPACT_F與branch_B的斷裂極限值相比較可知，撞擊力高于斷裂極限值時，branch_B發生斷裂；反之branch_B只有擺動，不發生斷裂.二者的接觸時間可以通過彈性力學公式計算得出，即

T=tcmp+trec=

(1)

(2)

根據力學相關知識，當碰撞部分是完全彈性碰撞時，tcmp=trec，彈性恢復系數為1；當碰撞部分是完全非彈性碰撞時，tcmp+trec=∝，彈性恢復系數為0，即碰撞后對象斷裂.令RbbA=∝，MbbA=∝，vpre_r_v=vpre_v，vpre_v為broken_branch_A碰撞branch_B前的速度，則接觸時間為

(3)

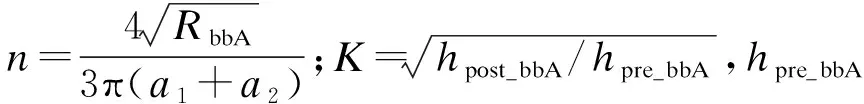
2.1.2 broken_branch_A水平方向與branch_B發生正向碰撞

復雜外力作用于broken_branch_A和branch_B時，當復雜外力與二者自身重力相差過大時，二者的重力可忽略不計，僅需考慮二者在復雜外力作用下在水平方向發生碰撞所構建的動態模型.二者發生碰撞時的撞擊力為

2.2 broken_branch_A和branch_B的側向碰撞

自然環境中無風、雨等外力作用或外力小于樹木自身重力的條件下，broken_branch_A與branch_B發生側向碰撞.

樹木對象表面不光滑，相互發生碰撞接觸時，broken_branch_A和branch_B的球體接觸點存在相互壓力NBA和NAB，即撞擊力IMPACT_F.接觸點切線方向上存在摩擦力fBA和fAB.由于二者發生側向碰撞，樹枝branch_B對broken_branch_A的NBA和fBA的合力方向也會偏離接觸點連心線，互相碰撞擠壓后的運動也將偏離原有的運動軌跡.

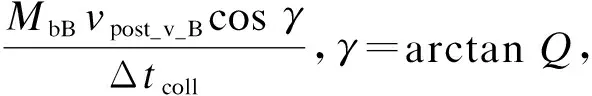
2.2.1 broken_branch_A在下落過程中與branch_B發生側向碰撞

broken_branch_A在下落途中與branch_B發生側向碰撞，圖1a為二者質量差距較小的情況，圖1b為branch_B質量明顯大于broken_branch_A質量的情況.

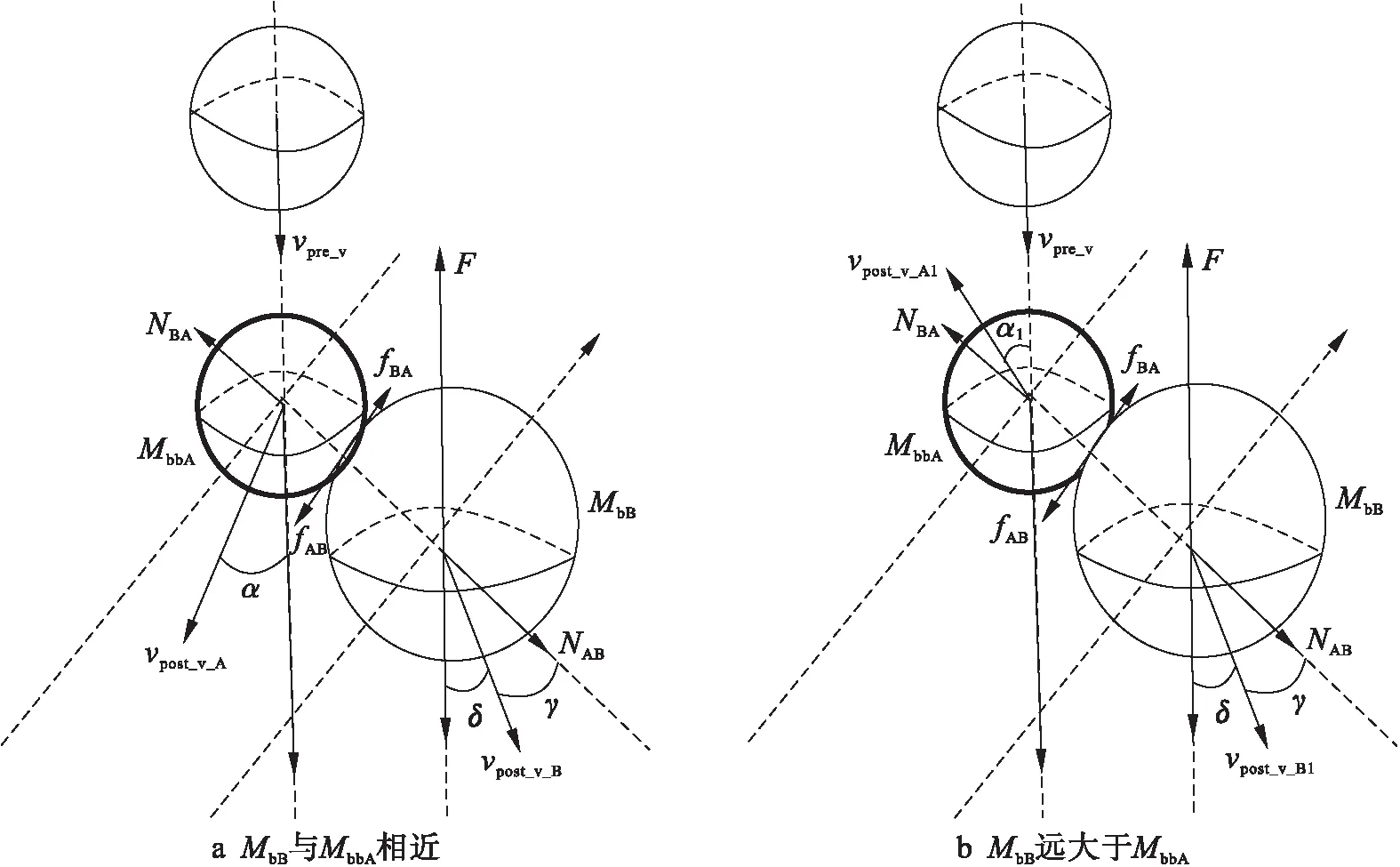
圖1 下落途中無外力作用下發生側向碰撞Fig.1 Side collision without external force in falling process

根據圖1a計算broken_branch_A和branch_B質量差距較小情況下發生側向碰撞后的vpost_v_A、vpost_v_B和α，其表達式為

式中：

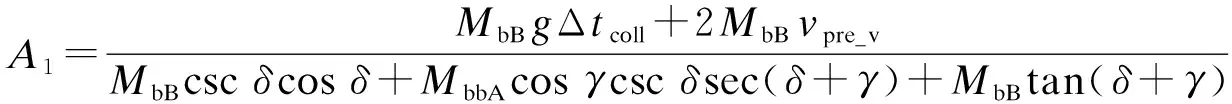
根據圖1b計算branch_B質量明顯大于broken_branch_A質量的條件下發生側向碰撞后的vpost_v_A1、vpost_v_B1和α1，其表達式為

2.2.2 broken_branch_A在上升過程中與branch_B發生側向碰撞

broken_branch_A在上升過程中與branch_B發生側向碰撞，圖2a為二者質量差距較小的情況，圖2b為branch_B質量明顯大于broken_branch_A質量的碰撞情況.

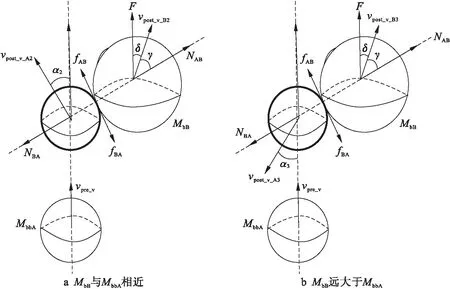
圖2 上升途中無外力作用下發生側向碰撞Fig.2 Side collision without external force in rising process

根據圖2a計算兩樹枝質量相差不大情況下發生側向碰撞后的vpost_v_A2、vpost_v_B2和α2，其表達式為

式中：

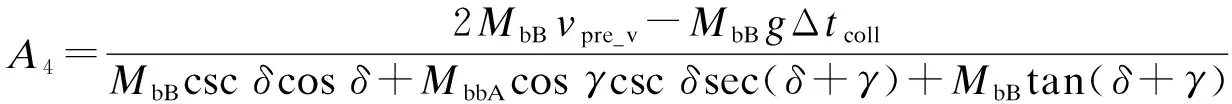
根據圖2b計算branch_B質量明顯大于broken_branch_A質量情況下發生側向碰撞后的vpost_v_A3、vpost_v_B3和α3，其表達式為

2.2.3 外力作用下broken_branch_A在下落過程中與branch_B發生側向碰撞

當外力與broken_branch_A重力相差較小時，或外力不可忽略的情況下，broken_branch_A在下落過程中與branch_B發生側向碰撞，圖3a為二者質量差距較小的情況，圖3b為branch_B質量明顯大于broken_branch_A質量的碰撞情況.

根據圖3a計算兩樹枝質量相差不大情況下發生側向碰撞后的vpost_v_A4、vpost_v_B4和α4，其表達式為

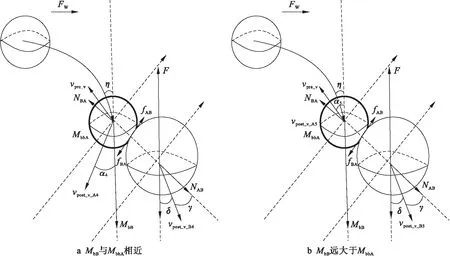
圖3 下落途中外力作用下發生側向碰撞Fig.3 Side collision with external force in falling process

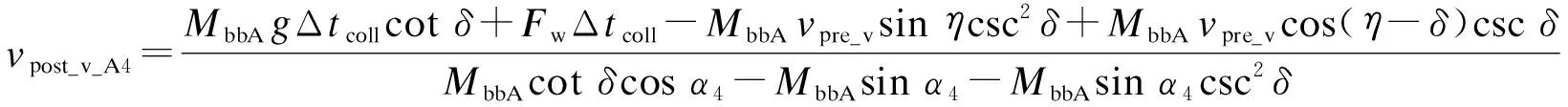
式中：

A7=cos(δ+γ-η)

A8=cos(δ+γ)

A9=A11/A10

A10=-MbBsin(δ+γ)+MbbAcscδcosγ+

MbBcos(δ+γ)cscδcosδ

A11=-MbBvpre_vA7+MbBA8vpre_vsinηcscδcosδ-MbBA8·

vpre_vcosη+MbbAvpre_vsinηcscδcosγ-MbBA8gΔtcoll

根據圖3b計算branch_B質量明顯大于broken_branch_A質量情況下發生側向碰撞后的vpost_v_A5、vpost_v_B5和α5，其表達式為

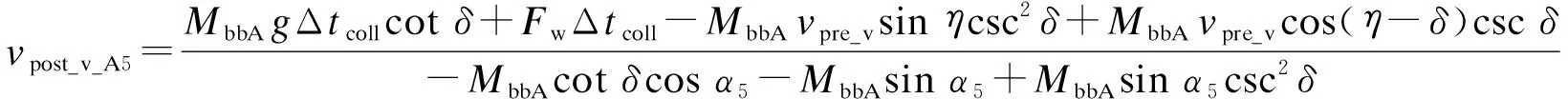
式中，

A12=-A11/A14

2.2.4 外力作用下broken_branch_A在上升過程中與branch_B發生側向碰撞

當外力與broken_branch_A重力相差較小時，或外力不可忽略的情況下，broken_branch_A在上升過程中與branch_B發生側向碰撞，圖4a為二者質量差距較小的情況，圖4b為branch_B質量明顯大于broken_branch_A質量的碰撞情況.

根據圖4a計算兩樹枝質量相差不大情況下發生側向碰撞后的vpost_v_A6、vpost_v_B6和α6，其表達式為

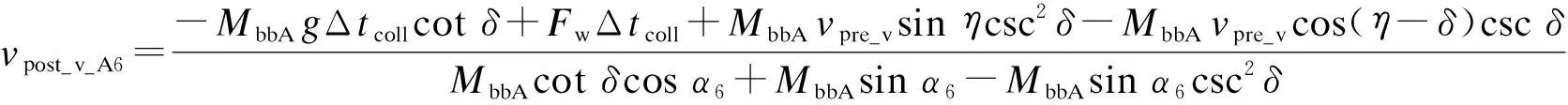
式中：

A13=A15/A14

A14=MbBsin(δ+γ)+MbbAcscδcosγ+

MbBcos(δ+γ)cscδcosδ

A15=MbBvpre_vA7-MbBA8vpre_vsinηcscδcosδ+

MbBA8vpre_vcosη-MbbAvpre_vsinηcscδcosγ-

MbBA8gΔtcoll

根據圖4b計算branch_B質量明顯大于broken_branch_A質量的情況下發生側向碰撞后的vpost_v_A7、vpost_v_B7和α7，其表達式為

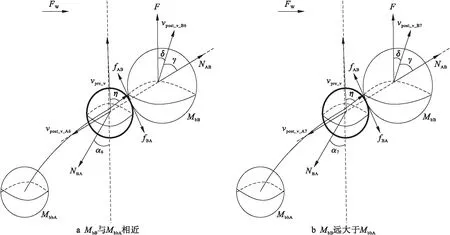
圖4 上升途中外力作用下發生側向碰撞Fig.4 Side collision with external force in rising process

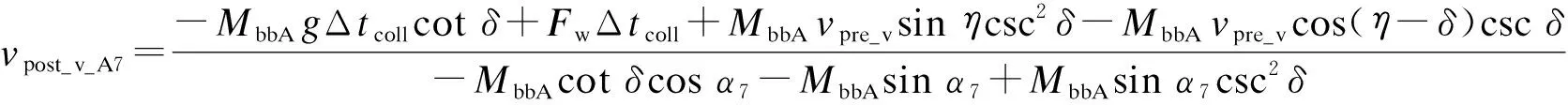
2.2.5 外力作用下broken_branch_A在水平方向上與branch_B發生側向碰撞

在自然界中，風等外力作用于broken_branch_A、branch_B時，外力遠遠大于二者自身重力時，broken_branch_A在外力作用下沿著外力方向做加速運動，示意圖如圖5所示.

根據圖5計算兩樹枝發生側向碰撞后的vpost_v_A8、vpost_v_B8和α8，其表達式為

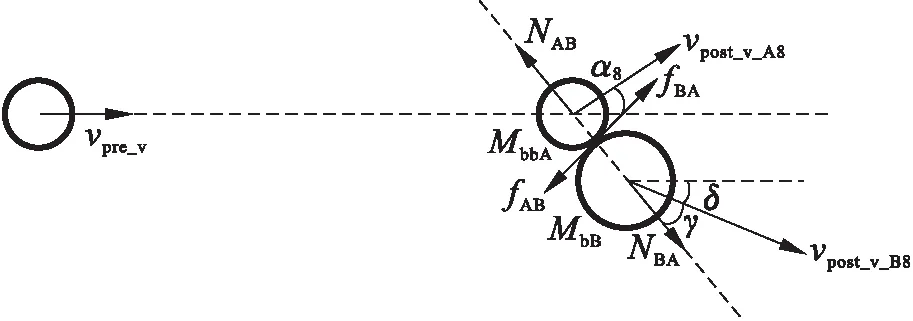
圖5 broken_branch_A和branch_B發生側向碰撞Fig.5 Side collision of broken_branch_A with branch_B

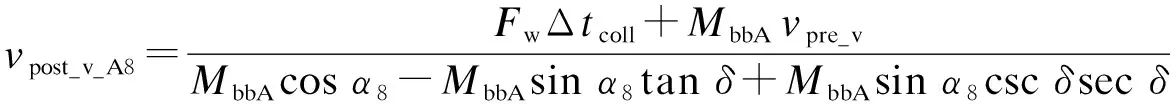
α8=arcsin(A16A17)

式中：

2.3 拋物線模型

2.3.1 broken_branch_A碰撞后的上升軌跡模型

broken_branch_A與branch_B在D(xD，yD)點發生碰撞后，broken_branch_A反向運動，反彈到E點后，在外力和自身重力作用下落地F點，示意圖如圖6所示.

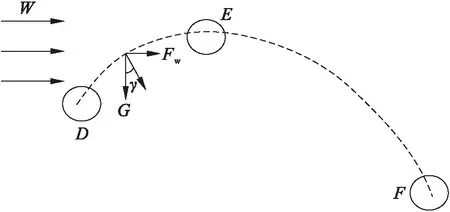
圖6 運動軌跡示意圖Fig.6 Schematic diagram of trajectory

2.3.2 broken_branch_A碰撞后運動過程中沒有接觸其他對象

broken_branch_A在自然界中斷裂后沒有接觸其他對象，broken_branch_A做拋物線運動直至落地，示意圖如圖7所示.

圖7 下落軌跡示意圖Fig.7 Schematic diagram of falling trajectory

3 實驗模擬

圖8為運動學模型成像圖.隨著風力的逐漸增大，樹枝逐漸傾斜，擺動幅度加大，最終發生斷裂.圖8a為1級風力情況下樹木的形態，枝干、葉片等無很大影響，樹木各部分對象呈現靜止狀態；圖8b為3級風力等級情況，可以看出當前風力等級對于細小的樹枝對象影響較大，部分枝葉對象開始呈現擺動的姿態；圖8c為4級風力等級情況，可以看出細小的樹木各分支對象圍繞著與上級枝干的連接處進行擺動，且擺動角度逐漸增大；圖8d為風力達到6級的情況，末級的樹枝、葉片等在風力作用下斷裂.通過基于運動學模型模擬出的效果，可以得到逼真的樹木運動姿態，模擬效果較為真實.

圖8 運動學模型成像圖Fig.8 Imaging by kinematic model

4 結 論

基于自然界中存在的復雜外力與重力間的關系、樹木分支對象間的碰撞角度，根據碰撞力學中的特征量獲得撞擊力及遭受碰撞后的樹木各分支對象的運動速度及角度等數據，建立樹木動態模型.采用該模型可以描繪各分支對象在斷裂后運動軌跡中接觸其他樹枝、葉片對象后而產生新的運動軌跡及擠壓、擺動等形態.經過實驗模擬，基于運動學構建的樹木動態模型具有復雜度低、系統反應迅速、效果真實等優點.