天然橡膠支座大變形壓剪性能的雙非線性超彈性理論和實驗研究

楊 靜，潘 文，蘇何先，何穎成，管慶松，張巖巖

(1. 昆明理工大學建筑工程學院，云南，昆明 650500；2. 云南省抗震工程技術研究中心，云南，昆明 650500；3. 震安科技股份有限公司，云南，昆明 650000；4. 云南省設計院第五建筑設計有限公司，云南，昆明 650000)

國內外多次地震證實，隔震結構的減震效果非常明顯。同時，考慮到未來需要對隔震建筑按更具體、更高的抗震設防目標進行性能化設計，隔震橡膠支座作為隔震結構的主要受力構件，有必要對其進行精細化分析研究。

隔震支座是由薄鋼板和橡膠交替粘結在一起的復合構件，它作為結構的局部構件，當結構受到外部激勵(靜力荷載、外部動力或地面加速度)時，構件的反應量有位移、速度、加速度，對于地震激勵，這些量的絕對值和相對值可能都是需要的；但與結構變形有關的相對位移最重要，只要支座每個受力狀態的位移確定，其內力及應力就可由每一瞬時的靜力分析確定[1]。因此，國內外學者基于靜力狀態對隔震橡膠支座進行了大量研究。

Haringx[2]是關于疊層橡膠支座性能的經典理論。該理論考慮了承受壓縮載荷和水平變形構件的水平剛度和屈曲載荷。但是，由于Haringx 理論是在假設材料線彈性的情況下推導的，因此無法將其直接用于評估變形較大的疊層橡膠的非線性行為。而后，Kelly[3]同樣基于材料線彈性假定，建立了數學物理模型并推導了隔震橡膠支座的水平剛度理論計算公式，并分析了支座的屈曲穩定。Chang 等[4]和Ding[5]分別采用解析剛度矩陣法和傳遞矩陣法，建立了離散的疊層橡膠支座的線性力學模型，該模型基于Haringx 理論，對具有不同幾何參數和材料性能的支座進行逐層分析，計算內力和位移。但是，在考慮彎矩剛度及材料屬性時，仍假設橡膠物理屬性為線性 (E=3G)[6-7]，未能反映大變形材料特性的非線性行為。Takaoka[8]建立了一種基于Haringx 理論的疊層橡膠支座非線性力學模型，但該模型預測疊層橡膠支座的大變形行為精度需取決于橡膠層的抗彎剛度和抗剪剛度非線性參數的合理設置。

在此背景下，本文基于Haringx 理論提出了一種天然疊層橡膠支座大變形壓剪狀態的雙非線性方法。它的特征是可以通過將材料非線性引入到支座等效勻質體的等效彈性模量Ec和彎曲剛度EcIs中，用EcA、EcIs表示支座變形的內力，建立微分平衡方程來表達大變形區域中的雙非線性行為。同時，結合實際工程中生產的足尺隔震支座的壓剪實驗，驗證了該方法的嚴密性和準確性。此外，隔震支座中橡膠屬于高分子聚合物，生產硫化過程中，已與硫化劑發生化學反應，具備了較高的彈性、耐熱性、延展性等[6-7]，可以認為隔震支座橡膠屬于理想超彈性材料，即不考慮變形對時間、溫度的依賴性。

目前，非線性固體力學的發展已經與材料微觀結構的發展緊密結合[9]。本文研究對象為隔震橡膠支座，其中，橡膠在微觀結構中存在明確的超彈性本構方程[10]。另外，一般物體在外力作用下會發生形狀和尺寸的改變，剪切模量G和體積模量K正是與這兩種不同類型的變形對應的兩個基本模量[11]，其中，G反映物體形狀的改變，K反映尺寸的變化。對于大多數材料，這兩個模量屬于同一量級，但是，對于特殊材料，如疊層隔震支座中的橡膠，其K值的量級則遠大于G，因此其壓縮變形將非常明顯地依賴于任何可能阻止形狀變化的邊界條件[11-12]。綜合考慮，有必要先從隔震疊層橡膠支座中隔離出單層橡膠進行受力分析。

1 單層橡膠單軸等效彈性模量和純彎剛度的推導

橡膠屬于各向同性材料[10]，因此，以下每個變形狀態，橡膠內部各點的剪切模量G均相同[9]。

1.1 推導單軸等效彈性模量

1.1.1 假設純壓運動量，引入位移函數

在實際工程中，因隔震層平面內剛度及支座豎向剛度都很大，豎向壓力作用下，豎向變形較均勻；且單層橡膠水平向受到上、下鋼板較大的約束。根據以上特點，作如下2 條假設：

1) 橡膠各點變形過程中，水平面保持不變；

2) 變形前的垂直線受豎向力后，各點變形后為拋物線，其中垂直線兩端與鋼板接觸各點無變形。物理坐標系如圖1 所示。

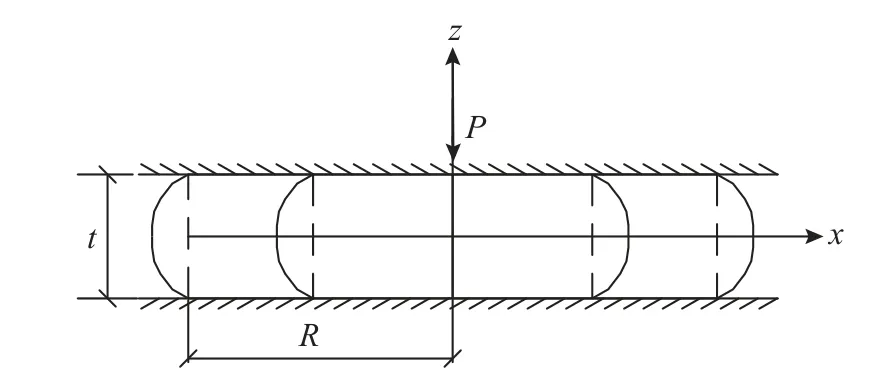
圖1 單層橡膠純壓變形圖Fig. 1 Single-layer rubber pure pressure deformation diagram

設未發生變形前，橡膠各點三維坐標為μ0(x,y),υ0(x,y),ω(z)。變形后，位移函數為：

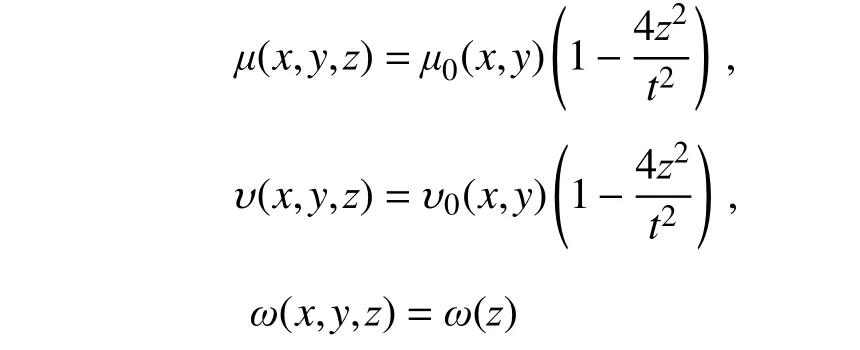
1.1.2 推導等效彈性模量

根據橡膠支座變形過程中體積保持不變[7,13]，略去線應變更高階的微量，其體應變為：

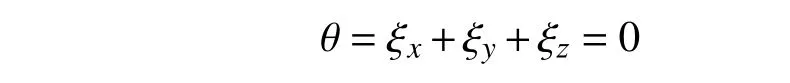
代入位移函數得：

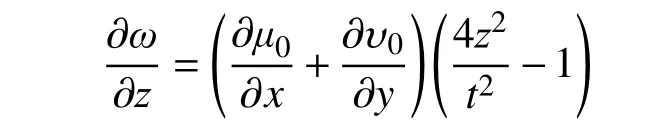
在厚度t范圍內，對變量z積分：

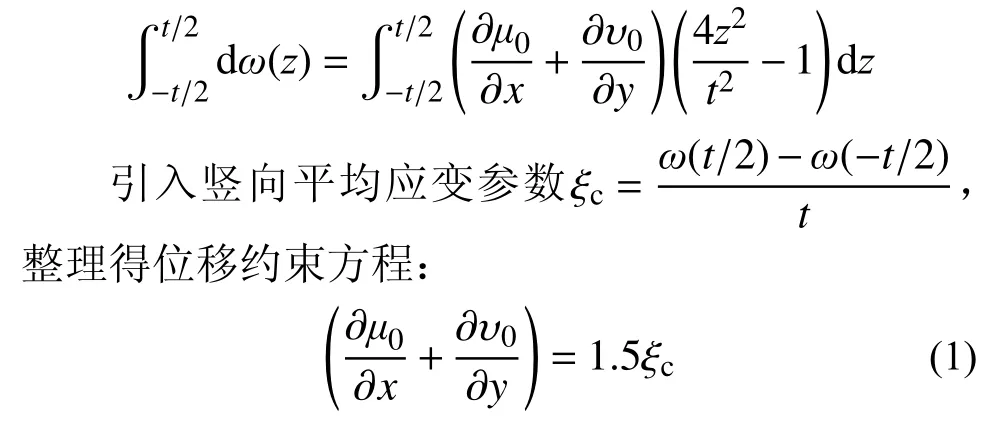
取單層橡膠任一點為微元體，其三維受力如圖2 所示。

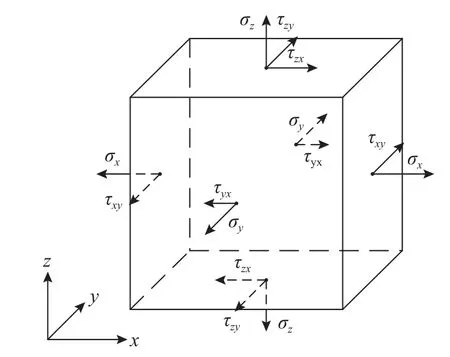
圖2 微元體受力圖Fig. 2 Micro-body force diagram

由幾何方程計算切應變：

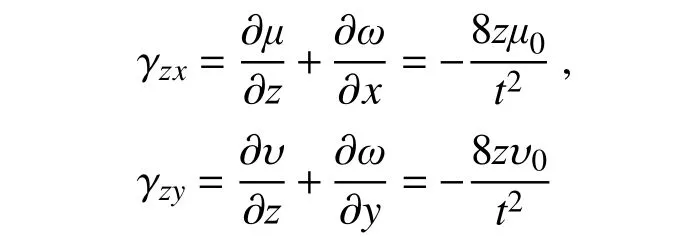
圓形橡膠支座的變形僅沿極坐標徑向方向：

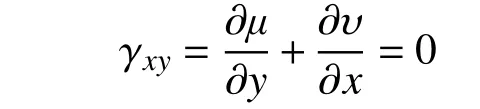
根據廣義胡克定律：

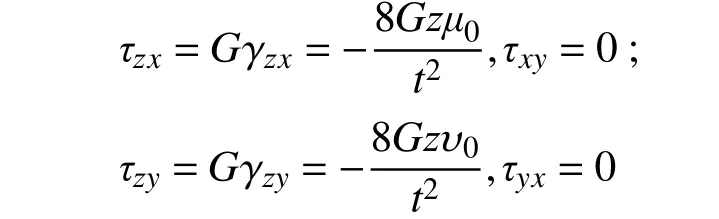
代入x、y方向平衡微分方程：

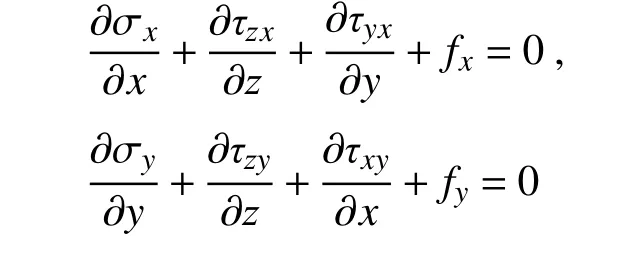
不考慮支座體力，得：

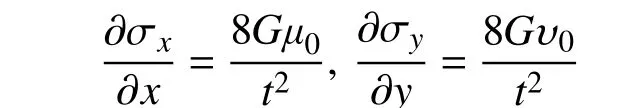
上兩式各對x、y求導，代入式(1)，得：

對于不可壓縮彈性固體，有內部約束方程[10]：

式中： σ為應力張量；S為法向偏張量；p為受力方向主應力。支座受力狀態處于非扭曲狀態，Sx=0,Sy=0，有：

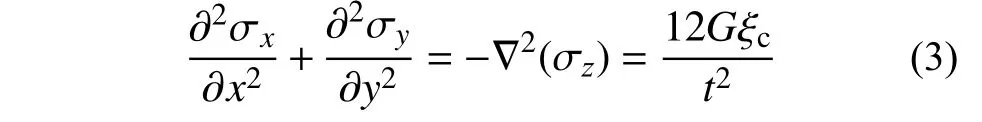
式(3)為應力 σz的調和函數[14]，即拉普拉斯算子，它的重要特點是，滿足此算子的變量，即使固體受力狀態屬于大變形，當與其他符合調和函數的變量相加減時，仍符合線性疊加原理。

在極坐標下，拉普拉斯算子存在簡單變換式[14]，且存在邊界條件r=R時 ， σz=0，則：

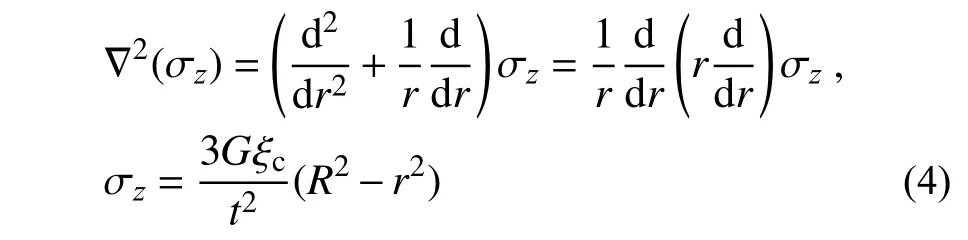
對式(4)兩邊在半徑R范圍內積分，得：

1.2 單層橡膠純彎等效彎曲剛度的推導

由1.1 節結論所得Ec，就可進一步推導壓剪支座與Ec相關的等效彎曲剛度。

1.2.1 假設純彎運動量，修正位移函數

單層橡膠層受彎矩作用時，作如下假設：

1) 因鋼板彎曲剛度很大，假設鋼板保持平面轉動，設相鄰鋼板之間的轉角為 α；

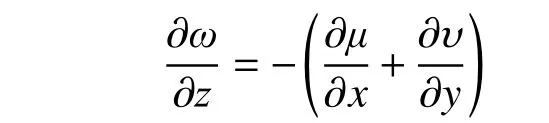
上式對x求導，得：

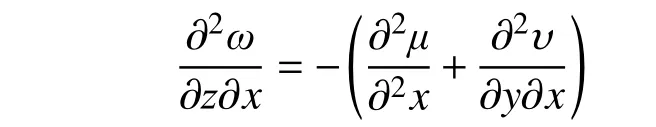
不考慮y方向扭轉，則有：

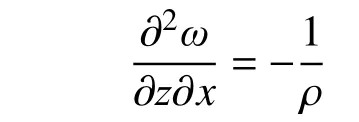
由邊界條件z=0 時 ，ω=0, ?ω/?z=0，得：

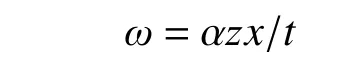
設未發生變形前，橡膠各點三維坐標為μ0(x,y), υ0(x,y),ω(z)；變形后，變形如圖3，且位移函數為：

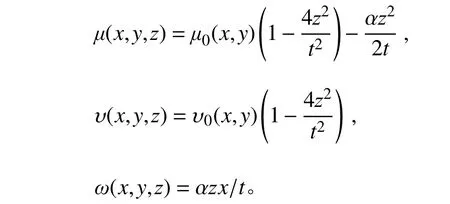
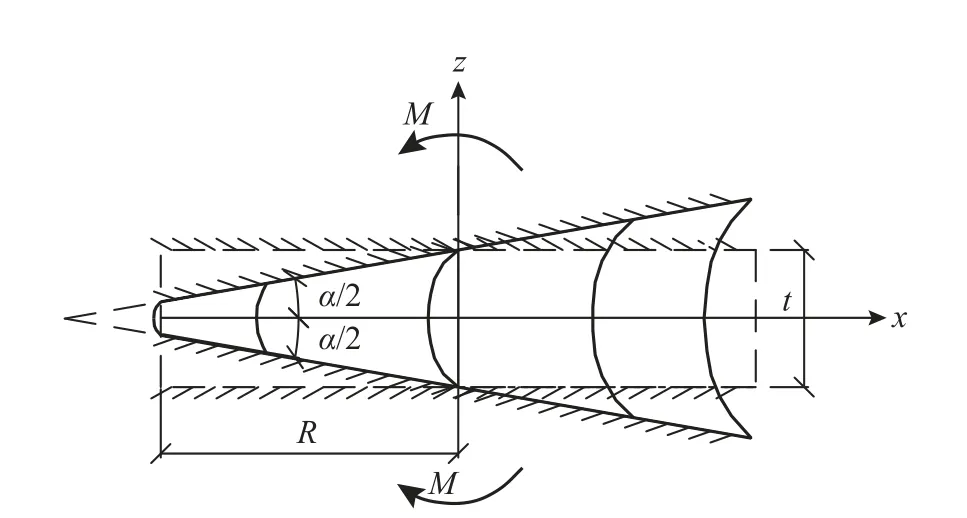
圖3 單層橡膠純彎變形圖Fig. 3 Single-layer rubber pure bending deformation diagram

1.2.2 推導純彎等效彎曲剛度

單層橡膠純彎調和函數的推導同1.1.2 節純軸壓，則有：

因彎曲關于y軸對稱，并由邊界條件，得豎向應力解析式：

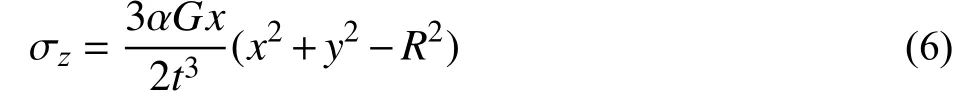
在極坐標下，應力對yz面求矩，并在整個截面上積分，求總截面彎矩：

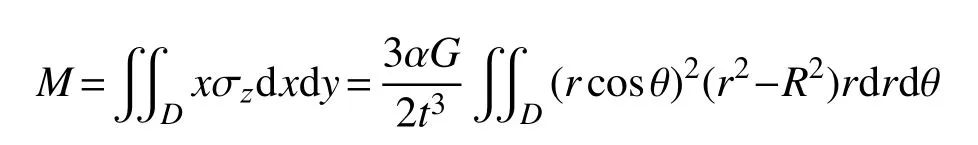
因截面轉動 α較小，引入鋼板轉動曲率半徑ρ，且截面直徑 2R≥t，則有： α ρ=t,1/ρ=α/t。

由1.1 節推導結論Ec，有：

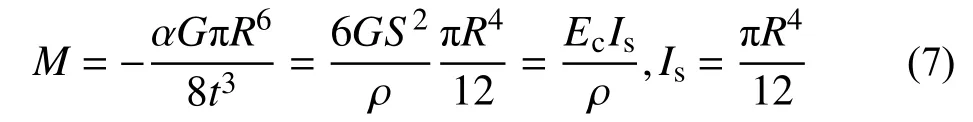
2 壓剪隔震橡膠支座數學模型方程的建立與通用解答

2.1 假設運動量，建立數學物理方程，并求通解

非線性連續介質力學研究物質宏觀層次的運動、變形與破壞，與微觀層次相比它是一個更加復雜的系統，它受制于微觀結構，又有自己獨特的規律，描述宏觀物體運動規律的方程一般是偏微分方程[9]。橡膠屬于易變形的固體，由其與鋼板交替粘結在一起的橡膠隔震支座，在豎向和水平荷載共同作用下會發生較大的水平位移和微小的彎曲變形，其運動形式簡單明確，可以通過建立偏微分方程反映隔震橡膠支座宏觀的運動、變形。

根據第1 節從橡膠微觀結構推導的Ec與EcIs，可以假設疊層橡膠支座為符合Ec與EcIs的等效均質體；同時，考慮到支座中剪切變形基本上由橡膠產生，均質體的幾何參數(As、Is)需考慮h/hr的放大系數[3](h為支座總高度、hr橡膠層總高度)。

在壓剪作用下，疊層橡膠支座產生較大的水平剪切變形，故假設支座水平位移μ為第一個運動未知量。支座軸線還會產生彎曲變形，但因支座彎曲剛度較大，則橫截面轉動變化也較小，可認為橫截面轉動后仍保持平面，但與變形后軸線不垂直，這是橡膠支座大變形的重要特征。為表示支座的彎曲變形程度，引入橫截面的轉角 β為第二個運動未知量。在幾何空間笛卡爾坐標系中(圖4)，設坐標橫軸為u，沿支座高度方向為坐標縱軸x。

根據彈性力學微元體幾何方程的推導原理，把橡膠支座作為有限大固體[14]，如圖5 所示，則最初相互垂直的線段OA與OB，運動到新平衡位置O′A′與O′B′時，二者之間角度的改變量θ，就是切應變。基于以上原理，將圖4 中均質體的下部分離體出來，則在剖面處，新橫截面上剪力為V=GAs(μ˙-β) ； 同時，轉角的導數 β˙(即為軸線上該點的曲率)，則新橫截面上彎矩為M=EcIsβ˙。由新截面上力的平衡及對中心點取矩，得平衡微分方程：

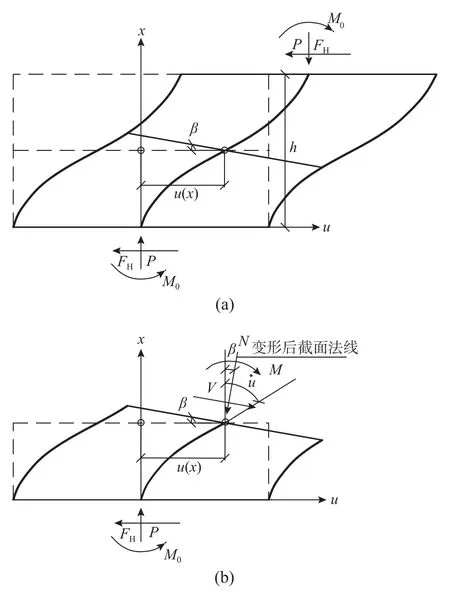
圖4 均質體支座數學物理簡圖Fig. 4 Mathematics and physics diagram of homogeneous body support

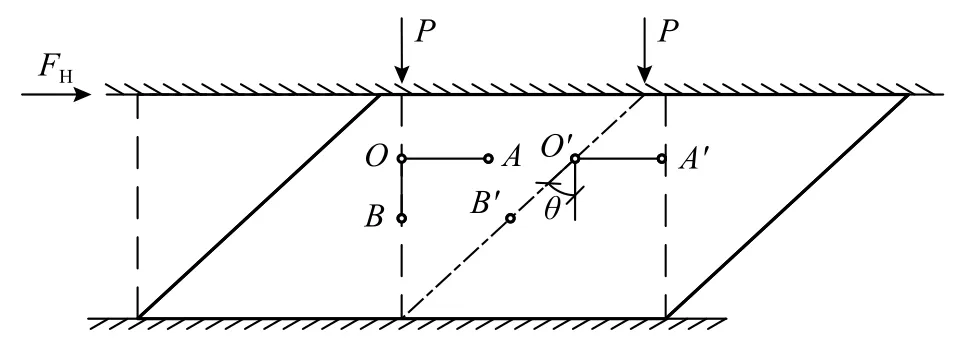
圖5 有限大支座幾何位移關系Fig. 5 Geometric displacement relations of finite bearings

因轉角很小，則 cosβ →1, sinβ →β，以上超越方程可簡化為：

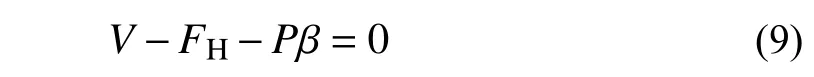
將M、V代入式(8)、式(9)得二元一階偏微分方程組：

求解關于μ、β的二元一階偏微分平衡方程。

隔震橡膠支座未知運動量μ、β的通用解答為：

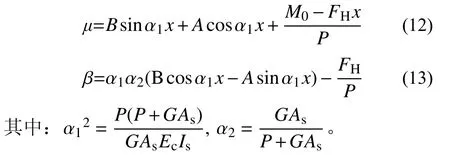
2.2 隔震橡膠支座運動量和內力的解析解

當支座上、下兩端不限制轉動時，式(12)、式(13)有未知常數A、B，其通解不能直接應用到隔震橡膠支座中。但因在實際工程中，橡膠隔震支座上、下截面分別與剛度較大的隔震層和下支墩相連接，相比之下，橡膠支座部分的剪切剛度較小，因此，支座數學物理模型簡化時，可假定支座上、下截面為固定端。基于此假定，橡膠支座頂部在水平剪力與軸力共同作用下，則其運動量方程式(12)、式(13)的邊界條件為：

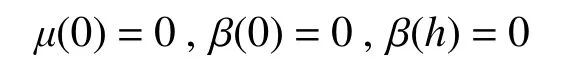
代入邊界條件，可求得方程中的未知常數：

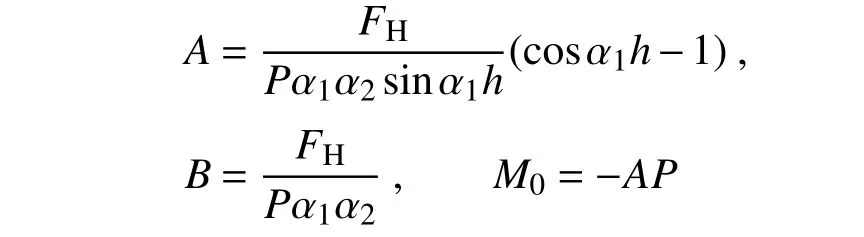
由此可知，在壓剪共同作用下，橡膠隔震支座任一橫截面水平位移μ與 轉角 β有唯一解答(軸壓P產 生的P-Δ效應，不需要反復迭代，即可求精確解)。且支座頂部的初始彎矩M0不獨立，它是關于P、FH的函數，從另一角度，在物理意義上，以上結論可解釋壓剪支座滿足變形協調方程。

最后，將所求運動量μ、β代入式(8)、式(9)，即得每個橫截面處對應內力M、V：

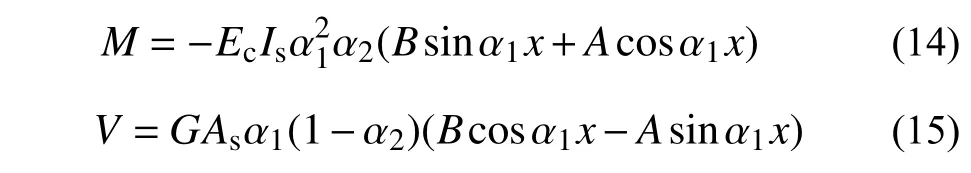
3 隔震橡膠支座的理論解與實驗結果對比分析

3.1 實驗隔震橡膠支座

本壓剪實驗選取實際隔震工程中的天然橡膠支座，其尺寸見表1。表2 則通過假設在等截面條件下，支座等效均質體與其他常用材料(混凝土與鋼材)的材料屬性對比。可知等效均質支座的剪切剛度遠小于鋼材與混凝土，而彎曲剛度接近等截面混凝土。從另一個方面驗證了第2 節中假定支座的剪切剛度很小、彎曲剛度很大是合理的。

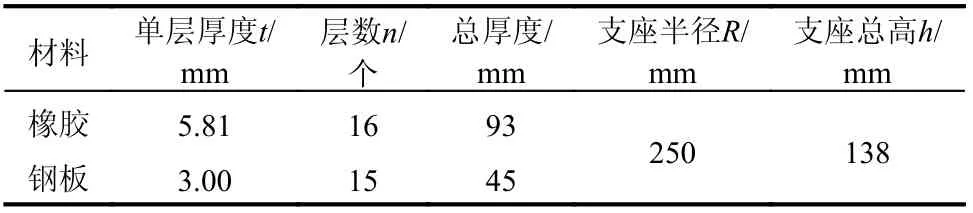
表1 橡膠支座尺寸Table 1 Size of rubber bearing

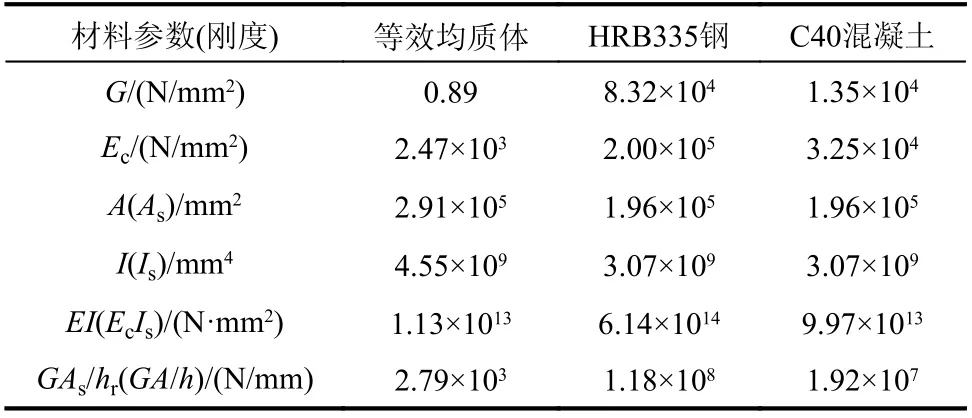
表2 等截面不同材料屬性對比Table 2 Comparison of different material properties of equal section

3.2 隔震橡膠支座壓剪實驗與其 G的合理選取

本次實驗加載設備為電液伺服壓剪試驗機(圖6)，其最大軸向壓力15 000 kN，水平最大動荷載1500 kN，豎向軸力按設計壓應力12 MPa 保持不變，緩慢施加水平荷載，最大剪應變400%(相當于最大水平位移377 mm)[15-16]。為消除橡膠粘性、蠕變及松弛等[17-18]其他性質的影響，取支座的第一個往復運動的1/4 曲線。其中加載曲線局部不光滑的原因，由于實驗設備受到了摩擦的影響[16]。

圖6 動態壓剪試驗機Fig. 6 Dynamic compression shear testing machine

在非線性連續介質力學中，當固體受到較大的變形時，變形和未變形構型的位置關系用變形梯度張量表示，而材料屬性與空間矢量關系通過柯西變形張量描述[10]。與初始狀態相比，支座在不同剪應變時，位置與材料屬性都發生較大改變。而由疊層橡膠支座實驗所得水平力與豎向、水平位移推導的G，綜合反映了支座在外力作用下，支座每個狀態幾何位置與材料屬性的雙非線性的改變。與1 節平衡微分方程中G反映了支座整體每個壓剪狀態的宏觀G相一致。

3.3 隔震橡膠支座 FH-γ 與 G-γ理論、實驗曲線對比分析

依據圖7 所示框圖，可由實驗曲線上每個壓剪狀態 γ 對應的G，迭代計算出該狀態橡膠支座的理論G與 γ值，同理，得出所有狀態的外力與變形FH-γ 理論曲線(圖8、圖9)。對比可知，FH-γ的實驗與理論曲線幾乎100%重合，說明考慮橡膠為非線性超彈材料時，壓剪隔震橡膠支座的理論解為精確解答。

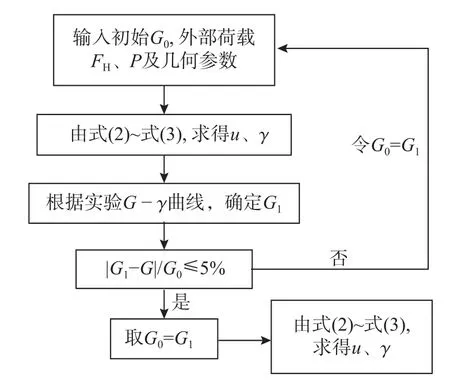
圖7 剪切模量G 與剪應變 γ計算程序框圖Fig. 7 Block diagram for calculation program of shear modulus G and shear strainγ

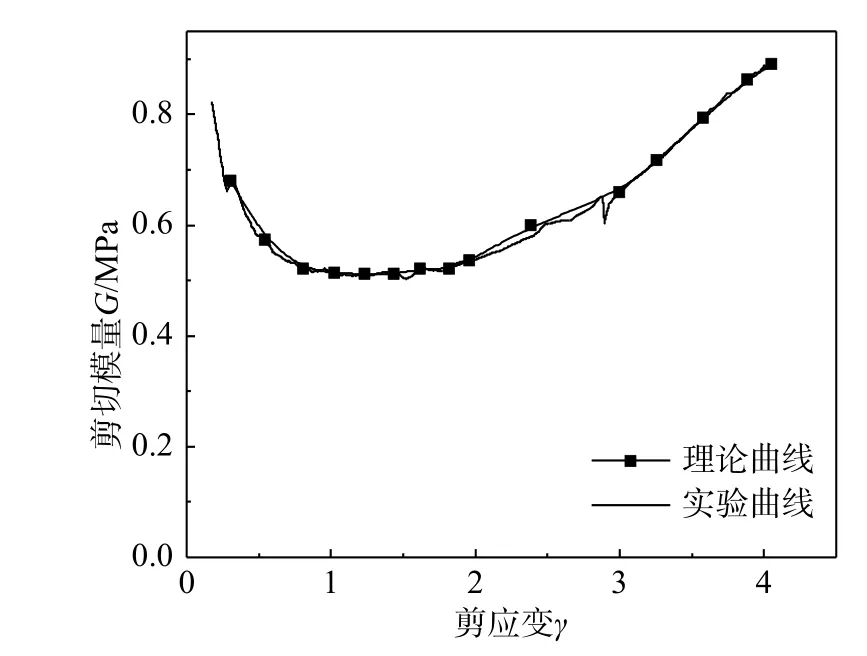
圖8 隔震橡膠支座壓剪 G-γ實驗、理論曲線(P=12 MPa)Fig. 8 Compression-shear G -γ experiment and theoretical curve of vibration isolation rubber bearing (P=12 MPa)

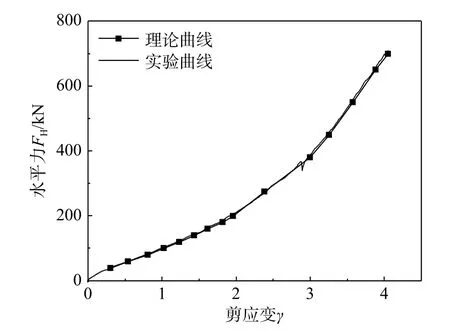
圖9 隔震橡膠支座 FH-γ理論、實驗曲線(P=12 MPa)Fig. 9 Compression-shear FH-γ experiment and theoretical curve of vibration isolation rubber bearing (P=12 MPa)

綜上所述，考慮到橡膠支座的整體剪壓變形和材料屬性的共同影響，《建筑隔震橡膠支座》GB/T 20688.3-2006[15]在確定橡膠支座多遇地震( γ=100% ) 、罕遇地震( γ=250% ) 的 γ 對應G時，采用足尺橡膠支座進行實驗是合理的。

4 隔震橡膠支座內力分布規律和剪應變、壓力相關性分析

4.1 橡膠支座各內力與運動量分布圖

基于前面系統的闡述推導，可對隔震支座某一個壓剪狀態進行受力分析，如隔震支座在最大水平推力FH=700 kN、P=12 MPa 作用下，可迭代計算出該狀態 γ=400%、G=0.89 MPa，進而可得各截面運動量及內力值(圖10)。由圖可知，橡膠支座最大水平位移出現在頂端，最大彎矩在支座兩端，最大剪力與轉角在支座中部。橫截面轉動角度均小于 1 ( 1=0.017 rad)，此處驗證了第2 節中假定勻質體的轉動角度 β較小是符合實際情況的。這些結論對于判斷支座產生破環的具體位置有一定的參考價值[19]。

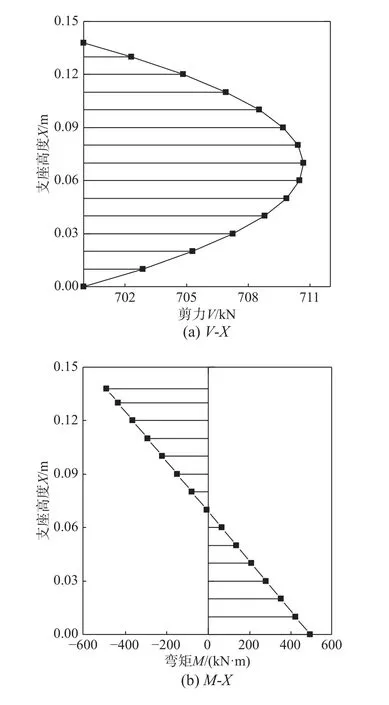
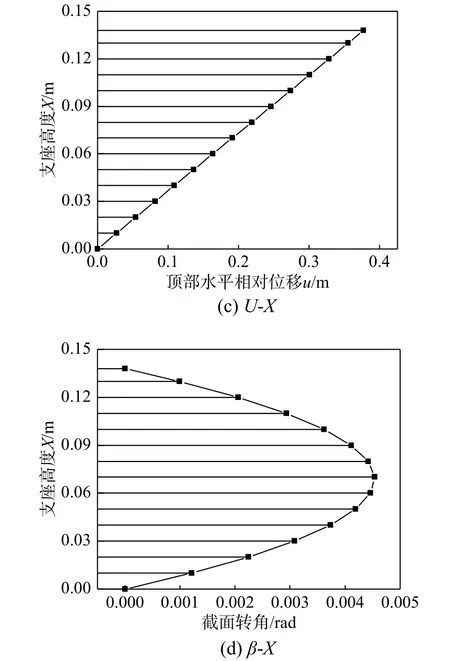
圖10 沿截面高度內力 M、V 及運動量 μ 、β的分布圖Fig. 10 Distribution diagram of internal force M、V and movement amount μ 、β along the section height

4.2 橡膠支座剪應變相關性分析

4.1 節中確定了橡膠支座最大內力所在的危險截面，將結論代入式(4)、式(6)及式(7)，可進一步確定此截面內各點的豎向應力。不同剪應變下，支座頂部沿水平推力軸線豎向應力分布圖11(P=12 MPa)。由圖可知，隨剪應變的增加，橡膠支座頂端截面壓應力較大區域的豎向壓應力逐漸增大，壓應力小的區域壓應力減小逐漸變為拉應力，且拉應力隨剪應變增加，絕對值也增加。但支座中心點的壓應力為定值，大小為2P/A[20]。

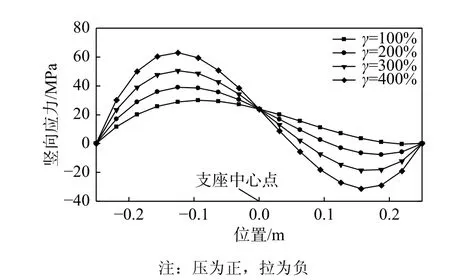
圖11 軸壓不變、不同剪應變時橡膠支座豎向應力分布圖Fig. 11 The vertical stress distribution diagram of the rubber bearing when the axial pressure is constant and the shear strain is different

4.3 軸壓變化引起效應P-Δ 與內力變化規律

為反映軸力變化對橡膠支座頂部水平位移及內力影響，仍選取4.1 節中支座的這一受力狀態(剪應變400%、軸壓應力P=12 MPa、G=0.89 MPa)。因剪應變不變，且實驗軸壓與設計壓應力差別不大時，橡膠G受壓力的影響較小，則不同軸力下，可不考慮支座G的變化[15]。將外力及G代入式(12)～式(14)，可得支座內力與位移理論解，且隨軸力的變化規律如圖12、表3 所示。

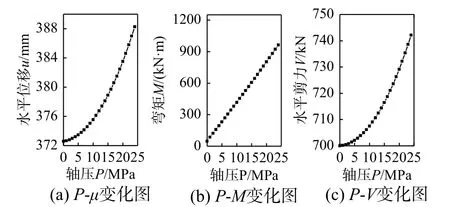
圖12 不同軸壓，支座頂端水平位移與內力變化圖Fig. 12 The horizontal displacement of the top of the support and the internal force change diagram under different axial pressure

表3 不同軸力下，支座頂部截面內力與水平位移理論值Table 3 The theoretical values of the internal force and horizontal displacement of the top section of the support,under different axial forces

由以上圖表可知，隨橡膠支座軸力增大，水平位移呈非線性增加，但增加比例不大，即P-Δ效應不明顯，但是，支座端彎矩增加較大，因此橡膠內應力隨軸壓的變化不可忽視[21-24]。

4.4 壓應力相關性分析

從圖13～圖15 可知，當剪應變越大時，軸壓改變引起豎向應力的變化越明顯，即壓力相關性強；而當剪應變小時，軸壓變化引起豎向應力的變化不明顯，即壓力相關性弱。

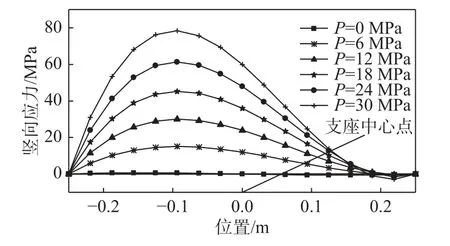
圖13 剪應變100%、不同軸壓支座頂部豎向應力變化圖Fig. 13 The vertical stress change diagram on the top of the support, with 100% shear strain and different axial compression

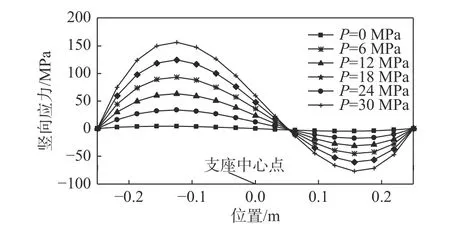
圖14 剪應變400%、不同軸壓支座頂部豎向應力變化圖Fig. 14 The vertical stress change diagram on the top of the support, with 400% shear strain and different axial compression

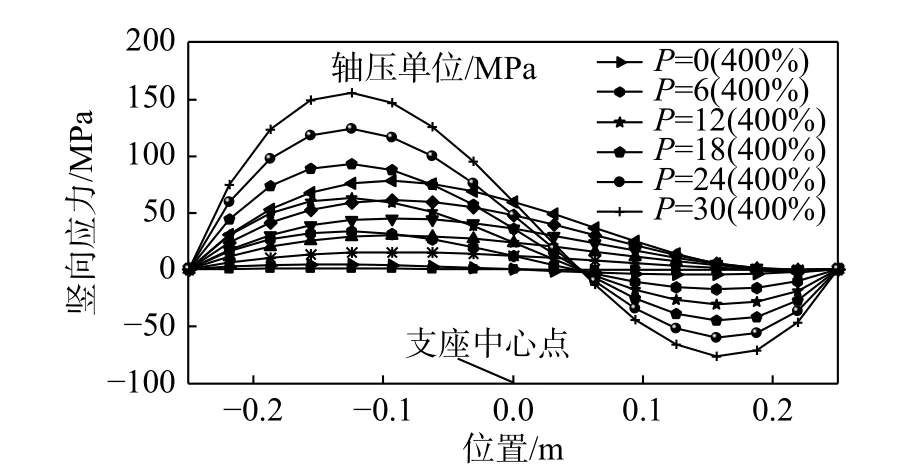
圖15 剪應變100%、400%，不同軸壓下支座頂部豎應力對比圖Fig. 15 Comparison of the vertical stress on the top of the support, when the shear strain is 100%, 400%,and different axial compressions

5 純剪隔震橡膠支座數學模型方程的建立與通用解答

當豎向軸力P=0，支座僅受水平力FH作用時，由于原微分方程中沒有了運動量的一次項，微分方程需要重新求解。

將P=0 代入式(10)、式(11)，得：

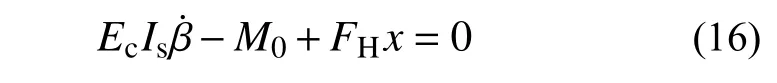
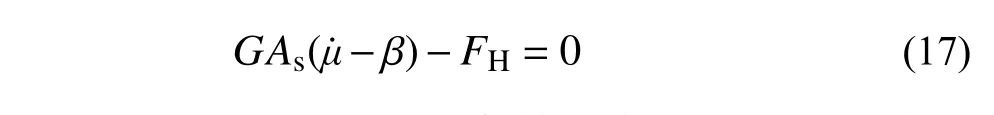
求解方程并由邊界條件得未知運動量及截面內力解答：

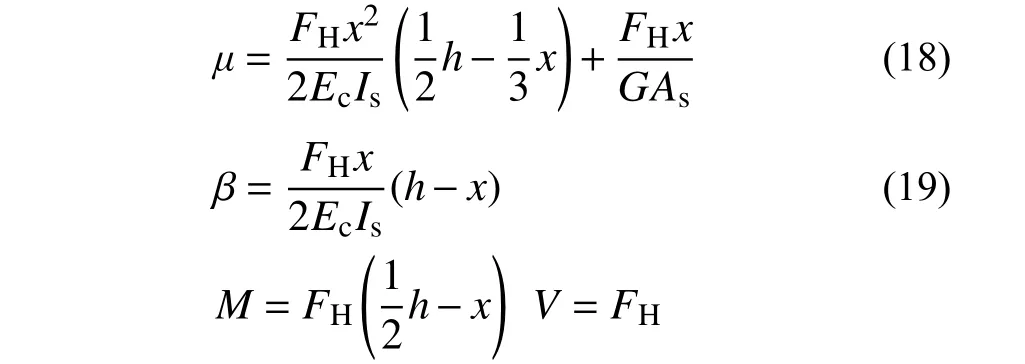
由式(18)可知，x=h時，支座頂部水平位移最大，即：

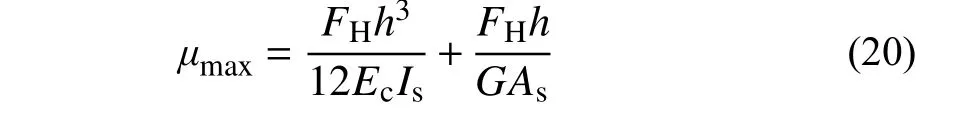
式(20)中第一項為彎曲引起的位移μE，對于長度遠大于橫截面尺寸的構件，其水平位移可以僅考慮第一項彎曲的影響，如工程中不考慮軸力影響的層間柱抗彎剛度；第二項為剪力貢獻的位移μG，對于高度與橫截面尺寸相近，而材料參數GAs?EcIs的構件，第二項提供了較大位移，如此文中的隔震橡膠支座，在水平力FH=700 kN 作用下，各項結果見表4，且可知式(20)與式(10)、式(11)在P=0 極限解答(見表3)相同。

表4 純剪切內力與位移理論值Table 4 Theoretical values of internal force and displacement in pure shear

6 結論

本文采用將橡膠材料的微觀結構和疊層橡膠支座的宏觀運動、變形相結合的方法，從數學的角度，結合物理運動學與靜力學，先后以單層橡膠和支座整體為研究對象，最后用關鍵性實驗來驗證理論結果，合理解釋了在水平、豎向荷載耦合作用下橡膠支座的幾何、材料雙非線性的大變形特征。主要得到以下結論：

(1) 根據單層橡膠推導結果的GAs與EcIs，建立了橡膠支座在兩種外部荷載同時作用下，反映水平變形與彎曲程度的偏微分平衡方程，得到了橡膠支座大剪切變形下，豎向與水平兩種荷載耦合作用下大剪切變形的幾何非線性通用解答。

(2) 因橡膠是各向同性材料，每個剪應變狀態，宏觀上支座有相同的剪切模量，但不同剪應變有不同的剪切模量。因此，確定各個狀態疊層橡膠支座的剪切模量非常重要。在第(1)部分理論解答基礎上，開展了實際工程中橡膠支座的壓剪實驗，依據實驗G-γ 曲線，得到支座FH-γ的理論曲線，與FH-γ實驗曲線幾乎完全重疊，解決了超彈性橡膠支座大剪切變形的材料非線性問題。

(3) 根據以上理論，對隔震支座某壓剪狀態進行受力分析，得到支座各截面運動量與內力解析式，可知，橡膠支座最大水平位移出現在頂端，最大彎矩在支座兩端，最大剪力與轉角在支座中部。這些結論對于判斷支座產生破環的具體位置有很好的參考價值。

(4) 剪應變不變，考慮軸力變化，得到以下規律，隨橡膠支座軸力增大，水平位移呈非線性增加，但增加比例不大，即P-Δ效應不明顯；而支座端彎矩增加較大，因而橡膠內應力隨軸壓的變化不可忽視。

(5) 為了驗證不同剪應變時，軸壓相關性的強弱，分別在剪應變100%、400%，施加變化的軸力，對比表明，當剪應變越大時，軸壓改變引起豎向應力的變化越明顯，即壓力相關性強；而當剪應變小時，軸壓變化引起豎向應力的變化不明顯，即壓力相關性弱。