一種抗強干擾的糾錯碼研究*

陳志勇 龍 華 劉海峰

（中國船舶集團有限公司第七二二研究所 武漢 430079）

1 引言

通信與密碼融合發(fā)展日益緊密，通信過程中的高效性與安全性往往是一對矛盾，若要求通信高效暢通，則需要簡化密碼安全協(xié)議流程及復(fù)雜度，甚至不用任何密碼保護，若要求通信安全可靠，則需要增加密碼保護及額外信息傳輸，則會降低通信質(zhì)量［1］。

密碼通信一般分為兩個階段，密碼同步階段和加密數(shù)據(jù)傳輸階段，如圖1所示。

密碼同步階段，發(fā)送方將IV 向量等密碼同步信息經(jīng)過信道編碼后發(fā)送給接收方，接收方對收到的數(shù)據(jù)信道譯碼，得到同步信息，并利用同步信息預(yù)置與發(fā)方相同的密碼機初態(tài)；數(shù)據(jù)傳輸階段，發(fā)送方對數(shù)據(jù)進行加密，經(jīng)過信道編碼后發(fā)送給接收方，接收方對接收到的信號信道譯碼，再對信息進行解密，得到明文信息。

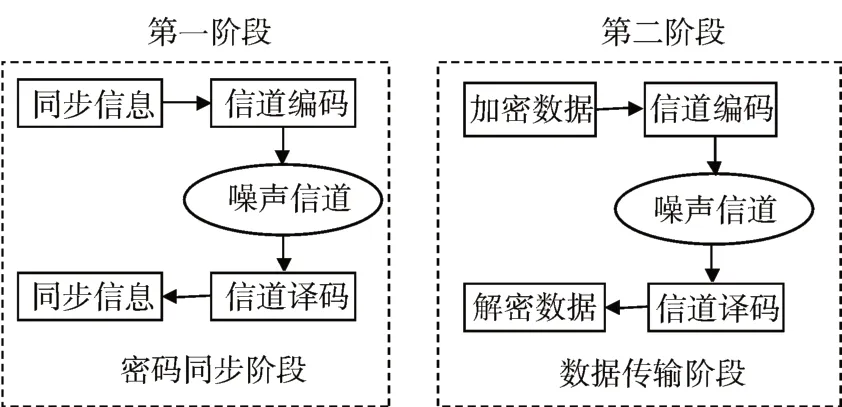
圖1 密碼通信系統(tǒng)圖

在某些人為干擾和自然環(huán)境噪聲干擾很強的情況下，信道誤碼率很高，經(jīng)常出現(xiàn)“明通密不通”的現(xiàn)象。分析該現(xiàn)象出現(xiàn)的原因，主要是由于明碼通信與密碼通信對信道誤碼的容忍度存在著差異。在密碼同步階段，同步信息一旦出現(xiàn)誤碼，收發(fā)雙方的密碼狀態(tài)不一致，將無法建立正確的密碼通信。在數(shù)據(jù)傳輸階段，在沒有錯誤擴散的情況下，少量的信道誤碼是可以容忍的。密碼同步階段必須使用同步概率非常高的糾錯編碼，才能保證“明通密也通”，因此，研究密碼同步碼的糾錯編碼具有非常重要的意義［2～4］。

2 編碼方案介紹

2.1 基本定義

定義1：在F2域上，分組碼[n，k]定義為信息長度k ，校驗長度r=n-k 的編碼，由信息位和校驗位組成長度為n 的序列(c0，c1，...，cn-1)稱為碼字，所有信息和相應(yīng)的碼字共有2k個，稱這2k個碼字的集合為[n，k]分組碼，定義R=k/n 為該分組碼的碼率。

定義2：兩個碼長為n 的碼字x、y 之間對應(yīng)位取值不同的個數(shù)，稱為該兩個碼字的漢明距離，記為d(x，y)。在分組碼[n，k]中，任意兩個碼字之間漢明距離的最小值，稱為該分組碼的最小漢明距離，記為

定義3：兩個碼長為n 的碼字x、y 之間對應(yīng)位取值相同的個數(shù)，稱為該兩個碼字的符合數(shù)，記為fh(x，y) 。符合數(shù)與漢明距離之間的關(guān)系為fh(x，y)=n-d(x，y)。

定義4：設(shè)f(x)=b0xk+b1xk-1+...+bk-1x+1 是k 次本原多項式，由f(x)可以生成線性移位寄存器序列，設(shè)初態(tài)為(a0，a1，...，ak-1)，則生成的序列為a0，a1，a2，...，方式如下：

2.2 編碼方案

線性分組碼[n，k]利用本原多項式生成移位寄存器序列，步驟如下：

1）在F2域上找到一個k 次本原多項式f(x)=b0xk+b1xk-1+...+bk-1x+1；

2）假設(shè)需要編碼的 k 比特信息為(a0，a1，...，ak-1)，使用方程式（1）生成長度為n 的移位寄存器序列，編碼后的碼字為(a0，a1，...，an-1)。

3）當(dāng)(a0，a1，...，ak-1) 取 遍（0，0，…，0）、（0，0，…，1），…，（1，1，…，1）共2k個信息元時，可以得到糾錯碼[n，k]的所有2k個碼字。

3 譯碼方案介紹

對糾錯碼[n，k] ，發(fā)送方將編碼后的碼字A=(a0，a1，...，an-1)通過信道傳輸?shù)浇邮辗剑邮辗绞盏酱a字R=(r0，r1，...，rn-1)，由于信道存在干擾，碼字R 中某些位置可能與A 序列中對應(yīng)位置的比特不同，信道中的干擾序列表示為E=(e0，e1，...，，en-1)有錯誤的位置ei取值為1，沒有錯誤的位置ej取值為0，則有R=A⊕E ，稱E 為信道的錯誤圖樣。信道干擾造成的錯誤可在序列中的任意位置出現(xiàn)，若發(fā)送的序列碼長為n，則信道中可能出現(xiàn)的錯誤圖樣E 有2n種。

如圖2 所示，A 是由本原多項式f(x)生成的線性序列，經(jīng)過噪聲干擾，相當(dāng)于模二加錯誤圖樣E ，得到的R 序列可以看成A 序列的含錯序列。接收方對R 序列進行譯碼，相當(dāng)于利用R 序列解線性移位寄存器序列的含錯方程組，求出A 序列的初態(tài)。從理論上說，當(dāng)序列長度n、移存器級數(shù)k 和含錯率p 滿足一定條件時是可以把移位寄存器的初態(tài)求出來的。

圖2 發(fā)送、接收、干擾序列三者關(guān)系

4 糾錯能力分析

本文對糾錯能力進行評估時，假設(shè)基于以下條件：

1）強干擾信道，信道誤碼率pe分別設(shè)為0.05、0.1、0.15，且誤碼隨機出現(xiàn)；

2）同步碼長度為設(shè)為32bit、64bit；

3）糾錯碼[n，k]中的參數(shù)k 設(shè)置為8，n 設(shè)置為24、32、40、48、56五種情況，對應(yīng)的碼率為1∕3、1∕4、1∕5、1∕6、1∕7；

4）用于比較的糾錯碼為重復(fù)碼和RS 碼，且碼率相當(dāng)。

4.1 糾錯碼同步概率計算公式推導(dǎo)

定理1［8］C 為線性分組碼，有以下性質(zhì)：

1）對 任 意 a，b，c ∈C ，d(a，b)+d(b，c)≥d(a，c)；

2）如果C 中任意兩個碼字的漢明距離≥2t+1，那么C 是可以糾正t 比特錯誤的糾錯碼。

根據(jù)定理1，可以由糾錯碼C 的最短漢明距離求得可糾錯比特數(shù)，表1 列出由f(x)=x8+x4+x3+x2+1 生成的糾錯碼［24，8］、［32，8］、［40，8］、［48，8］、［56，8］的最短漢明距離及可糾錯比特數(shù)。

定理2［8］：假設(shè)糾錯碼C 的最短漢明距離為2t+1，當(dāng)錯誤比特數(shù)≥t+1 時，一定可以找到不能糾正過來的碼字。

表1 五種糾錯碼的可糾錯比特數(shù)

定理2 的證明中，通過構(gòu)造法找到不能糾正的碼字，但是在實際信道中錯誤碼是隨機出現(xiàn)的，存在大量錯誤比特數(shù)≥t+1 卻可以正確譯碼的情況，表2 列舉了在信道誤碼率為pe=0.1，糾錯碼為［40，8］，試驗次數(shù)為100000 次的糾錯情況。當(dāng)錯誤比特數(shù)為7、8、9、10 時，絕大多數(shù)的錯誤均可糾正，只是隨著錯誤比特數(shù)變多，糾錯能力越來越低，說明該編碼在錯誤比特數(shù)超過理論糾錯能力情況下，仍然有一部分是可以糾錯的［9～10］。

表2 ［40，8］糾錯碼糾錯情況

下面分兩步推導(dǎo)該糾錯碼的錯誤譯碼概率公式。

1）計算長度為n 的碼字出現(xiàn)t 比特錯誤的概率

假設(shè)信道誤碼率為pe，長度為n 的碼字隨機出現(xiàn)t 比特錯誤，概率pt服從二項分布，計算公式為

2）計算出現(xiàn)t 比特錯誤的情況下譯碼錯誤的概率

接收碼字為r ，要在2k個碼字中找與之比特符合數(shù)最大的碼字，作為它的譯碼。

假設(shè)發(fā)送的碼字為a，接收的碼字為r，出現(xiàn)t比特錯誤，則a 與r 的比特符合率為pt'=(n-t)/n，隨機情況下，兩條序列比特符合率p0=0.5，兩條序列的符合個數(shù)服從正態(tài)分布。可以由正態(tài)分布公式計算長度為n 的序列出現(xiàn)t 比特錯誤的T 值：

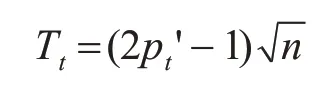
一方面，如果在C 中存在與碼字r 之間漢明距離為t-1 的碼字b，根據(jù)譯碼規(guī)則，一定會把r 譯成b，從而出現(xiàn)譯碼錯誤。b 與r 的比特符合率為p't-1=(n-t+1)/n，可以計算長度為n 的序列出現(xiàn)t-1個錯誤的T 值：

圖3是兩個碼字漢明距離概率的正態(tài)分布圖。

圖3 碼字漢明矩離概率正態(tài)分布圖

pb表示C 中碼字與r 之間漢明距離≤t-1 的概率，pb可以由Tt-1反查正態(tài)分布表得到，該概率是一定會將碼字r 譯成錯誤碼字b 的概率。由于C 中共有2k個碼字，任一個都可能與碼字r 之間漢明距離≤t-1，所以一定會譯錯的概率為2k×pb。

另一方面，還存在其他碼字c 與碼字r 之間漢明距離等于t 而譯錯的情況，有50%的可能將碼字r 錯誤地譯成碼字c。在圖3 中，pa為T 值≥Tt的概率，由Tt反查正態(tài)分布表可得到，而pc=pa-pb為存在某個碼字c 與碼字r 之間漢明距離等于t 的概率，由于C 中共有256 個碼字，任一個都可能與碼字r 之間漢明距離等于t ，并有50%概率譯錯，所以此種情況譯錯的概率為2k×0.5×pc。綜合以上兩方面，當(dāng)錯誤比特為t 時，譯碼錯誤的概率為

當(dāng)p*t ≥1.0 時，表示出現(xiàn)t 比特錯誤時，一定會譯碼錯誤。

綜合1）和2），長度為n 的碼字出現(xiàn)t 比特錯誤并譯碼錯誤的概率為pt×p*t，由此可以求出總的譯碼錯誤概率：

表3 是糾錯碼［40，8］在信道誤碼率為0.1 條件下，錯誤比特數(shù)為0～14時，譯碼錯誤概率分布表。

糾錯碼［40，8］在信道誤碼率為0.1 條件下，總的錯誤譯碼率為0.002231，糾錯碼［40，8］的譯碼成功率為0.997769。當(dāng)傳輸32bit 或64bit 同步碼時，需要用糾錯碼［40，8］進行4 次或8 次編碼，則傳輸32bit 同步碼成功概率為0.9977694=0.9911，傳輸64bit 同步碼成功概率為0.9977698=0.9823，以上理論計算結(jié)果與模擬實驗結(jié)果完全吻合。

表3 ［40，8］糾錯碼譯碼錯誤概率分布

4.2 與RS碼和重復(fù)碼的糾錯能力比較

在強干擾信道條件下，將該糾錯碼與RS碼、重復(fù)碼的糾錯能力進行比較研究。

1）RS碼的糾錯能力

RS[n，k]表示對數(shù)據(jù)進行RS編碼，信息長度為k 字節(jié)，編碼后數(shù)據(jù)長度為n 字節(jié)。 RS[n，k]碼能糾正任何(n-k)/2 個隨機字節(jié)錯誤。設(shè)信道誤碼率為pe，單字節(jié)正確傳輸?shù)母怕蕿閜s=(1-pe)8，由二項分布公式可推導(dǎo)RS[n，k]編碼正確傳輸?shù)母怕蕿椋?1～13］

2）重復(fù)碼的糾錯能力

重復(fù)碼是對每一比特經(jīng)過n 次重復(fù)傳輸，以擇多方式進行糾錯的糾錯碼。n 一般為奇數(shù)，設(shè)信道誤碼率為pe，單比特譯碼正確的概率為

對k 比特信息重復(fù)傳輸n 次，接收方通過糾錯后正確接收的概率為p=psk。

3）糾錯能力比較

表4 是本文研究的糾錯碼與RS 碼、重復(fù)碼在強干擾信道條件下、碼率相同情況下的糾錯能力比較，誤碼率設(shè)為0.05、0.1、0.15，同步碼長度設(shè)為32bit、64bit，碼率設(shè)為1∕3、1∕4、1∕5、1∕6、1∕7。

圖4 是信道誤碼率為0.1 時，該糾錯碼與RS碼、重復(fù)碼糾錯能力進行比較的結(jié)果。

表4 強干擾信道條件下糾錯能力比較

圖4 三種糾錯碼碼率與同步概率曲線

5 結(jié)語

本文對基于線性移位寄存器序列的糾錯碼進行研究，利用正態(tài)分布理論，給出了同步碼糾錯概率的計算公式，與RS 碼和重復(fù)碼等常用編碼方案比較的結(jié)果顯示，在強干擾高誤碼率信道條件下，利用該糾錯編碼方案，糾錯能力更強，加密傳輸可靠性更高，具有抗強干擾特性。