基于改進GM（0，N）的艦船裝備維修費預測模型*

何鵬翔 孫勝祥

（1.海軍工程大學管理工程與裝備經濟系 武漢 430033）（2.91306部隊 上海 200000）

1 引言

隨著新時代海軍艦船裝備建設的快速發展，各種大型艦船陸續服役，其中部分艦船也集中進入了修理期，在艦船裝備維修經費總量有限的前提下，經費的供需矛盾日益突出。為了合理確定新型艦船計劃修理費用，提高裝備經費的使用效益，迫切需要對新型艦船的計劃修理費用進行準確的預測。

傳統裝備費用估算方法主要有工程法、類比法、參數法等，文獻［1～2］運用工程法、類比法和參數法等方法對于艦船裝備和戰斗飛機不同時期的費用進行了估算；文獻［3～4］分別運用支持向量機和案例推理的方法對艦船裝備維修費進行了預測，但模型的預測精度取決于樣本數據的數量，數據的樣本較少時，預測精度往往不高。大型艦船裝備一般都是單艦或者小批量生產，樣本數據較少，灰色預測方法作為灰色系統理論的主要成果，主要針對小樣本、貧信息的不確定系統進行研究［5～7］，對于艦船裝備維修費預測有很強的適用性。文獻［8］從擾動解大小的角度證明了GM（0，N）模型更加適用于小樣本建模。但艦船裝備和其他復雜裝備相比，其維修費與建造費、排水量等因素有著更加緊密的關系，建造費相似的艦船其維修費往往也是更為接近的。而文獻［8］中僅僅依據相似度對于樣本進行重新排序，并不能充分顯現相似程度更高的艦船裝備對于待測樣本維修費的影響。

本文擬在利用距離熵分析樣本之間相似度的基礎上，利用累積法代替傳統GM（0，N）中的參數估計方法，從而賦予相似度較大的樣本更大的權重，使相似度較小的樣本占據更小的權重，從而達到提高艦船裝備維修費預測精度的目的。

2 GM（0，N）模型的基本原理

GM（0，N）模型通過利用原始數據累加后的灰色數據序列進行建模，可以在一定程度上弱化原始數據的隨機性，提高數據序列的規律性，其模型計算過程如下［7］：

1）計算原始數據序列的一階累加生成序列；

2）構造數據矩陣；

3）利用最小二乘法求得參數估計列：

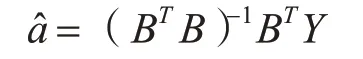
4）計算模型的預測值：

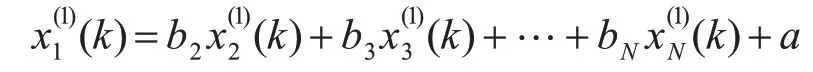
但由于艦船裝備維修費影響因素眾多［9］，且會隨著管理體制及相關政策的變化而變化，不確定性強，建造費、排水量等因素往往與維修費有著很強的正相關關系，根據支配原理，艦船裝備維修費之間也必然存在著相似性，相似程度更高的樣本對于維修費變化規律的影響也會更大，直接將原始數據依據累加法進行建模雖然可以弱化數據的隨機性，但并沒有考慮艦船裝備的相似度對于待測樣本的影響。

3 艦船裝備維修費預測模型構建

考慮到艦船裝備維修費與建造費、自身性能參數等因素緊密相關，基于“相似信息優先”原理對GM（0，N）模型運用累積法進行改進。

3.1 基于距離熵的相似度度量

熵作為一種衡量系統不確定狀態的方法，與傳統判斷相似度的方法相比，可以利用現有信息推算出更多有價值的信息量，從而降低主觀因素對于計算結果的影響［10］。如果將艦船裝備看作一個復雜的系統，可以將信息熵用于判斷不同艦船裝備之間的相似度，系統的總熵值最小，包含的信息量也是最大的，艦船裝備之間的相似度也最高。設艦船裝備樣本A0，A1，A2，…，An，每個樣本又有m 個參數y1，y2，…，ym，xij則表示第i 個樣本關于第j 個參數的指標數據。待測樣本A0與Ai之間關于yj參數歐氏距離的比重vij為

則樣本A0與Ai的距離熵為

其中i=1，2，…，n；j=1，2，…，m。

距離熵越小，則表示樣本A0與Ai之間的性能參數信息越相似，在后續建立預測模型時，也應當賦予更多的權重。

3.2 基于相似信息優先累積的模型構建

在參數估計中，使用最多的方法是最小二乘法，該方法誤差處理時需要基于誤差平方和最小化的假設，但該假設是難以驗證的，同時也容易造成模型估計與參數實際值相偏離。而累積法則不需要對于模型誤差進行假設，該方法對樣本數據進行加權和累加，進而估計模型參數，可以使預測的誤差趨向于零［11～12］。但是，一般累積法可能會導致相似程度越低的信息占據更高的權重，而相似程度越高的信息卻占據較低權重［13］的情況，從而使得模型的估計產生一定的偏差。

因此，本文提出一種基于相似信息優先的累積法。首先，通過對樣本進行重新排序改變累積法的累積權重，使得相似程度越高的信息占據的權重越大，而與待測艦船裝備越相似的樣本數據也可以更好地反映維修費與各參數之間的關系。然后，使用該方法對GM（0，N）的參數進行估計，進而優化其預測結果。

假設相似信息優先累積算子的最高階數為r，模型的參數為N。對于相似程度更高的樣本，其數據累加的次數也越多。將相似信息優先的累積算子運用于GM（0，N）模型的方程式兩邊，可以得到下列方程組：

其中，x(1)

i(k)為重新排序后的原始數據序列的一階累積生成序列，且

則方程組可以用矩陣形式表示為

在傳統GM（0，N）模型的參數估計中，A矩陣的行數一般取決于模型中艦船樣本的數量。當樣本量n 小于艦船裝備性能參數N 時，則無法用傳統最小二乘法進行求解，還需要首先對裝備的參數進行篩選，容易出現一些關鍵影響因素被剔除的問題。而在運用累積法計算時，A 矩陣的行數則取決于階數r。因此，可以通過調整累積運算的階數對于A矩陣的行數進行調整，令累加算子的階數與艦船裝備的輸入參數相同，避免出現當樣本量較少而相關參數較多模型無法計算的問題。

當r = N 時，只有矩陣A 中出現某一行的元素全部為0 或者任意兩行（列）元素相等時，矩陣A 才為奇異矩陣。但是對于艦船裝備而言，不同的艦船其輸入參數及有關費用肯定是不可能完全一致的，同時也不存在數據為零的情況。因此，在累積GM（0，N）中，矩陣A的逆矩陣一定是存在的，對于參數的求解則可以直接表示為

則可求出艦船裝備維修費預測GM（0，N）模型為

通過式（7）累減還原后，可以得到艦船裝備維修費的預測值。

3.3 改進的GM（0，N）模型預測步驟

改進的GM（0，N）模型預測步驟如下。

Step 1：根據式（1）和式（2）計算原始數據樣本與待測艦船裝備之間的距離熵；

Step 2：依據距離熵的值，按照從大到小的順序對樣本重新排序并計算一階累加生成序列；

Step 3：對于重新排序后的數據，利用累積法根據式（5）計算參數估計值a，b2，b3，…，bn；

Step 4：將模型參數估計值代入式（6）即可得到改進GM（0，N）模型，再通過式（7）累減還原即可得到待測艦船裝備的維修費。

4 案例分析

本文通過調研所得數據見表1（相關數據已經進行過脫密處理），運用本文所提出的改進GM（0，N）模型對艦船裝備維修費進行預測，以驗證本文提出方法的可行性。

表1 艦船裝備計劃修理費用與性能參數原始數據表

首先，采用基于距離熵的相似度的計算方法，求得艦船裝備樣本F 與A、B、C、D、E 之間的距離熵分別為0.89、0.70、0.78、0.91、0.80；

1）將樣本按照距離熵從小到大進行重新排序：B、C、E、A、D，并計算一階累加生成序列；

2）計算模型參數：a?=A-1*Y= [0.1136 -0.1720-0.1213 18.6993]；

3）基于相似累積法GM（0，N）模型的預測公式為

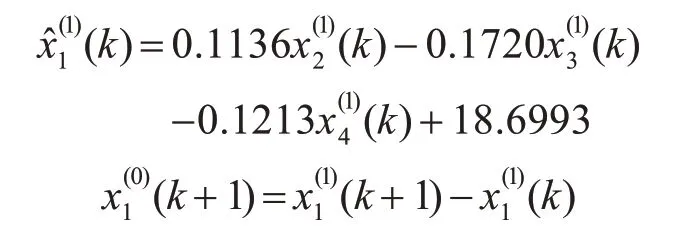
模型的擬合精度和預測精度分別如表2所示。

表2 擬合精度對比表

同時，本文采用文獻［8］中的方法也進行了預測，結果見表2。從表2可以看出，本文提出的預測模型對于F 艦船裝備維修費的預測值與實際值的相對誤差為4.33%，優于文獻［8］所提模型的相對誤差8.74%；從圖1 也可以直觀地看到本文的模型在數據擬合時穩定性要比傳統模型好，傳統模型擬合的平均相對誤差為3.85%、最大相對誤差高達9.23%，而改進GM（0，N）模型平均相對誤差僅為0.85%、最大相對誤差只有1.90%。由此可見，與傳統GM（0，N）模型相比，本文所提出的相似信息累積GM（0，N）模型可以更加充分地利用與待測樣本相似程度更高的信息，有利于提高模型預測的穩定性和精度。

圖1 兩種模型的擬合誤差比較

5 結語

隨著大型艦船裝備陸續進入修理期，對于維修費用計劃的制定也提出了更高的要求，考慮到現有方法在處理小樣本數據時的不足，本文提出一種基于相似優先累積的GM（0，N）模型。該方法在利用距離熵判斷樣本之間相似度的基礎上對樣本進行重新排序，再利用累積法代替最小二乘法對于參數進行估計，同時也解決了樣本量較少時無法用最小二乘法對于模型參數進行估計的問題，更加充分發揮了灰色預測模型在處理小樣本數據時的優勢。對于新型艦船裝備維修費用的估算有較強的實用性，也為利用參數法進行維修費估算從灰色理論的角度提供了新的解決方案。該方法實用性較強，也可以用于其他大型復雜裝備的修理費用預測。