強基計劃數學備考系列講座(6)
——集合與函數(上)

王雪芹 王慧興

(1.北京師范大學第二附屬中學 2.清華大學附屬中學)

高校強基計劃校考試題與高考試題突出互補性,本文基于這種互補性構建“集合與函數”學習輔導.

1 知識與技能

1.1 集合

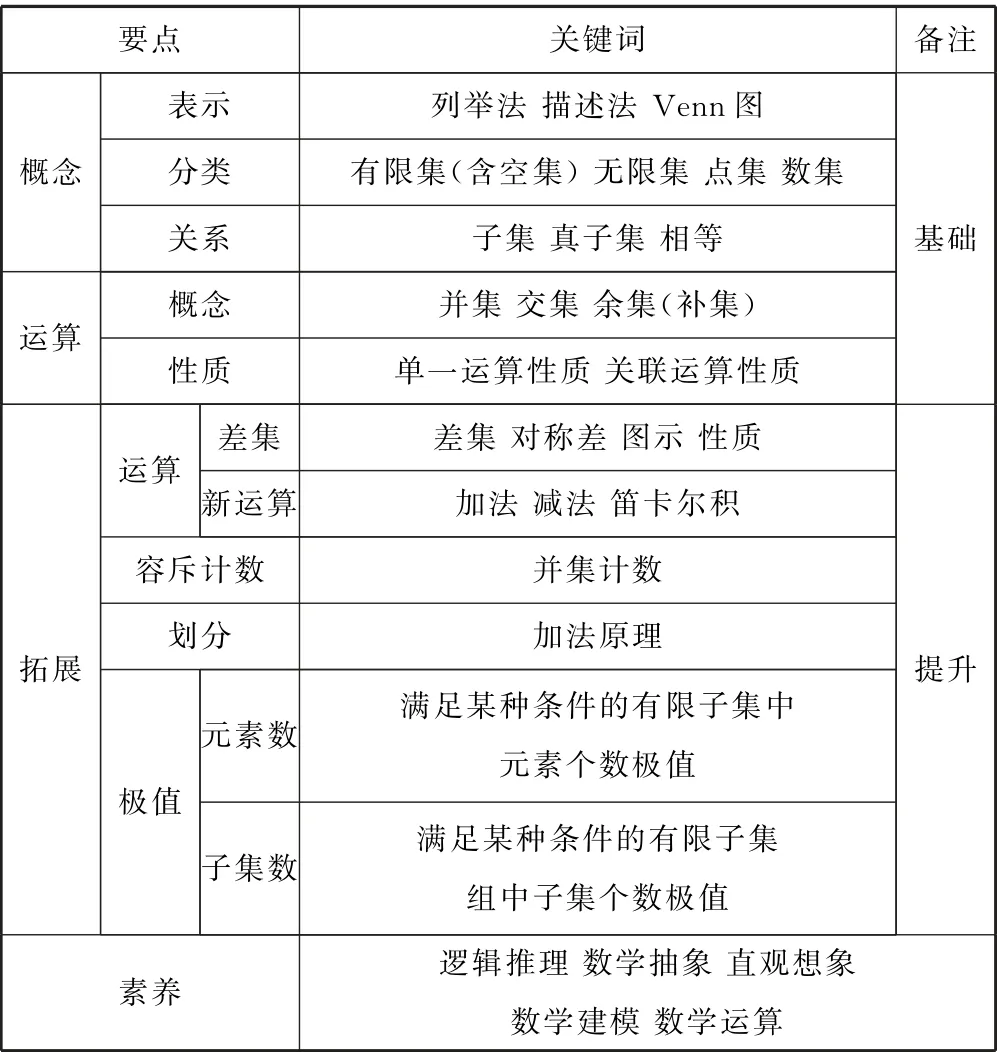
表1

1.2 常用邏輯

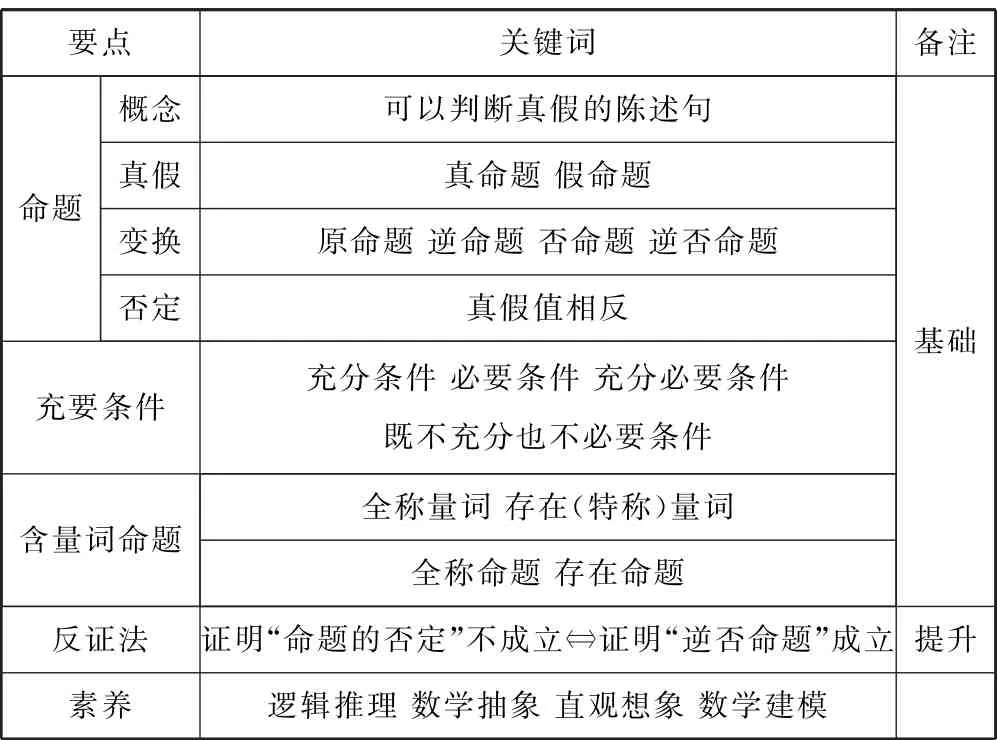
表2

1.3 函數

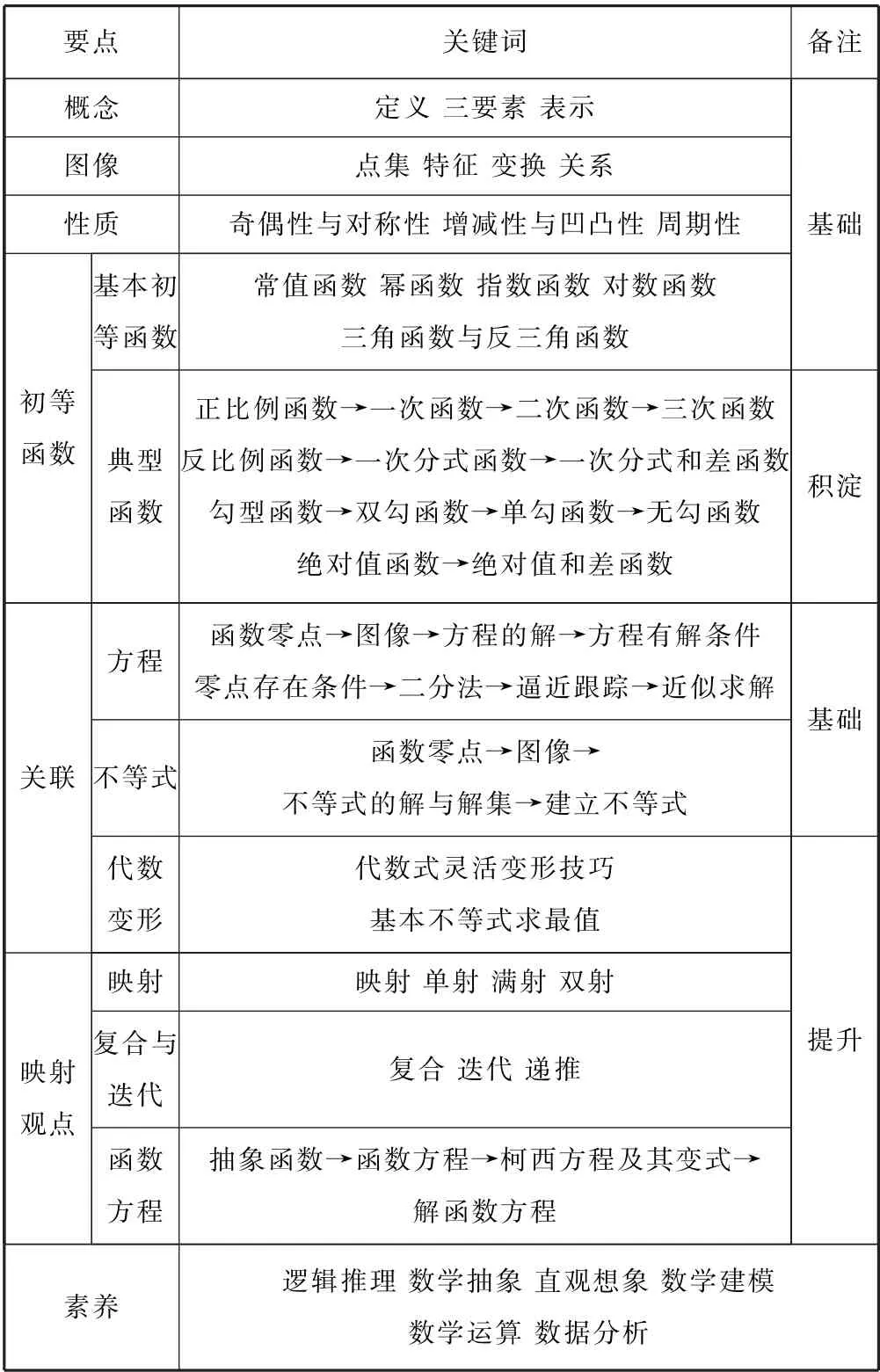
表3

2 要點解析

2.1 反證法

準確提出反證假設,由之出發,經邏輯推理,揭示出矛盾,得出反證假設不成立,從而肯定欲證命題成立.反證法是間接論證命題的一種方法,其本質是證明“原命題的否定”不成立,或論證其“逆否命題”成立；提出反證假設,融入已知,相當于增加一個條件,再進行推理,目標是構建矛盾.

2.2 集合運算關聯性質

設U為全集,集合A,B,C?U,記集合X(X?U)的補集為ˉX＝?UX.

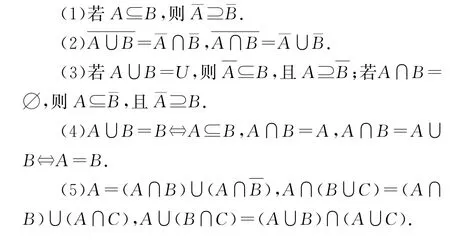
2.3 差集與對稱差

(1)差集:AB＝{x|x∈A,x?B}.

(2)對稱差:AΔB＝(AB)∪(BA)＝(A∪B)(A∩B).

(3)A∩B＝A(AB)；通常A(AB)?B,特別地,當B?A時,有A(AB)＝B.

(4)記有限集合X的元素個數為|X|,則對有限集合A,B,有|A∪B|＝|A|＋|B|－|A∩B|,特別地,當A∩B＝?時,有

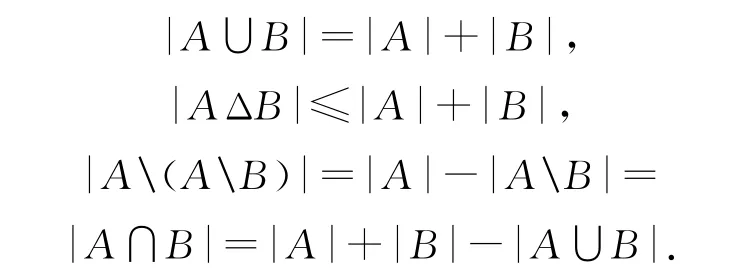
(5)若非空有限集合A,B滿足|A∩B|＝1,則|A|＋|B|≥3.

2.4 集合之間定義加法、減法、乘法等新運算

(1)加法:A＋B＝{a＋b|a∈A,b∈B}.

(2)減法:A－B＝{a－b|a∈A,b∈B}.

(3)數乘:kA＝{ka|a∈A}.

(4)乘法:A·B＝{ab|a∈A,b∈B}.

(5)笛卡爾積:A×B＝{(a,b)|a∈A,b∈B},坐標平面點集R2＝{(x,y)|x,y∈R}.

2.5 集合劃分與加法原理

(1)集合劃分:如果集合S的一組兩兩交集都是空集的非空子集A1,A2,…,An,滿足A1∪A2∪…∪An＝S,則稱子集組{A1,A2,…,An}構成集合S的一個n-劃分；對任意一子集A?S,都有

A＝(A∩A1)∪(A∩A2)∪…∪(A∩An).

加法原理:對有限集合S的任意一n-劃分{A1,A2,…,An},都有|S|＝|A1|＋|A2|＋…＋|An|.

(2)容斥計數原理:對任意一組有限子集A1,

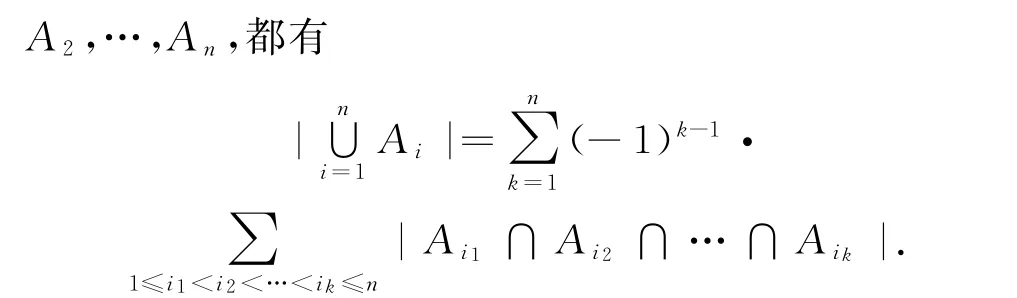
2.6 子集極值

(3)子集極值有兩類問題,其一是滿足某種條件的子集中元素個數最多或最少的問題,其二是滿足某種條件的子集組中子集個數最多或最少的問題.

2.7 函數圖像

函數圖像提供直觀想象情境,函數y＝f(x)(x∈D)的圖像是指點集Ff＝{(x,f(x))|x∈D}在坐標系中的可視化表現,通常是一條曲線,或一個點列.其基本特征:任意一垂直于x軸的直線至多與這條曲線有一個公共點,要把握各種典型函數的圖像.

2.8 數形結合

基于圖像建立不等式是不等式證明與多元最值探究的一項基本技能,也是學以致用的根本要求.例如,基于函數y＝sinx圖像,可以建立如下不等式:

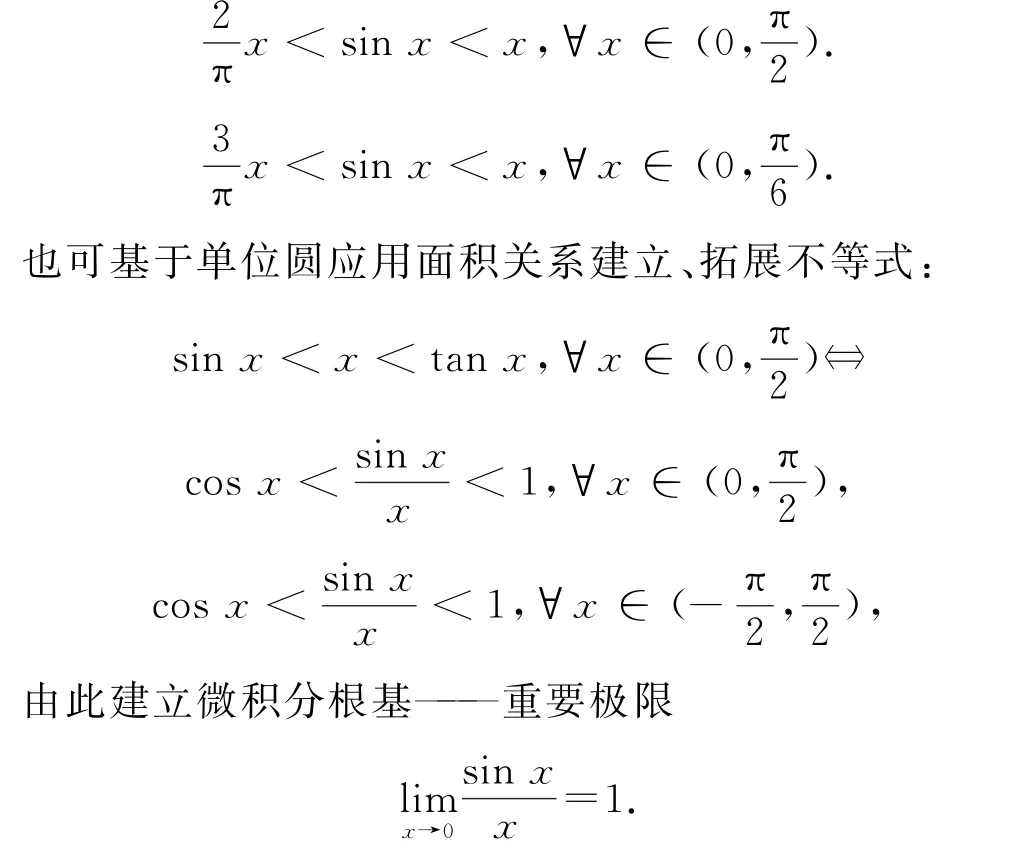
2.9 典型函數

我們在初等函數中提出典型函數概念,它由基本初等函數建構,分為兩個層次,把不需要借助導數工具就能理解性質與作圖的一些初等函數稱為第一類典型函數,而把需要應用導函數才能分析性質與作圖的一些初等函數稱為第二類典型函數,第一類典型函數分為如下五條主線,如表4所示.

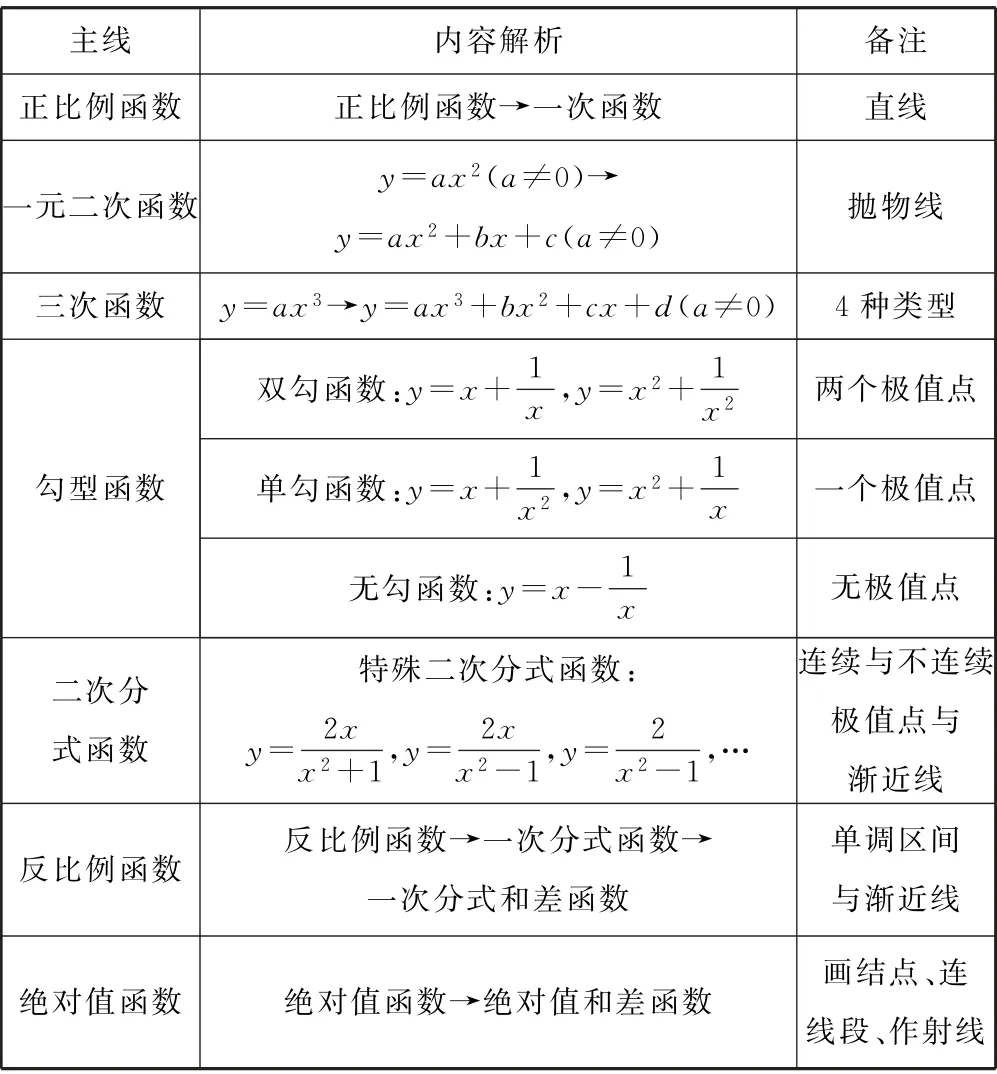
表4

2.10 映射抽象

設函數y＝f(x)(x∈D)的值域記作M,從定義域到值域上的映射f:D→M,當這個映射是雙射時,就有逆映射f－1:M→D,由此定義反函數y＝f－1(x)(x∈M).

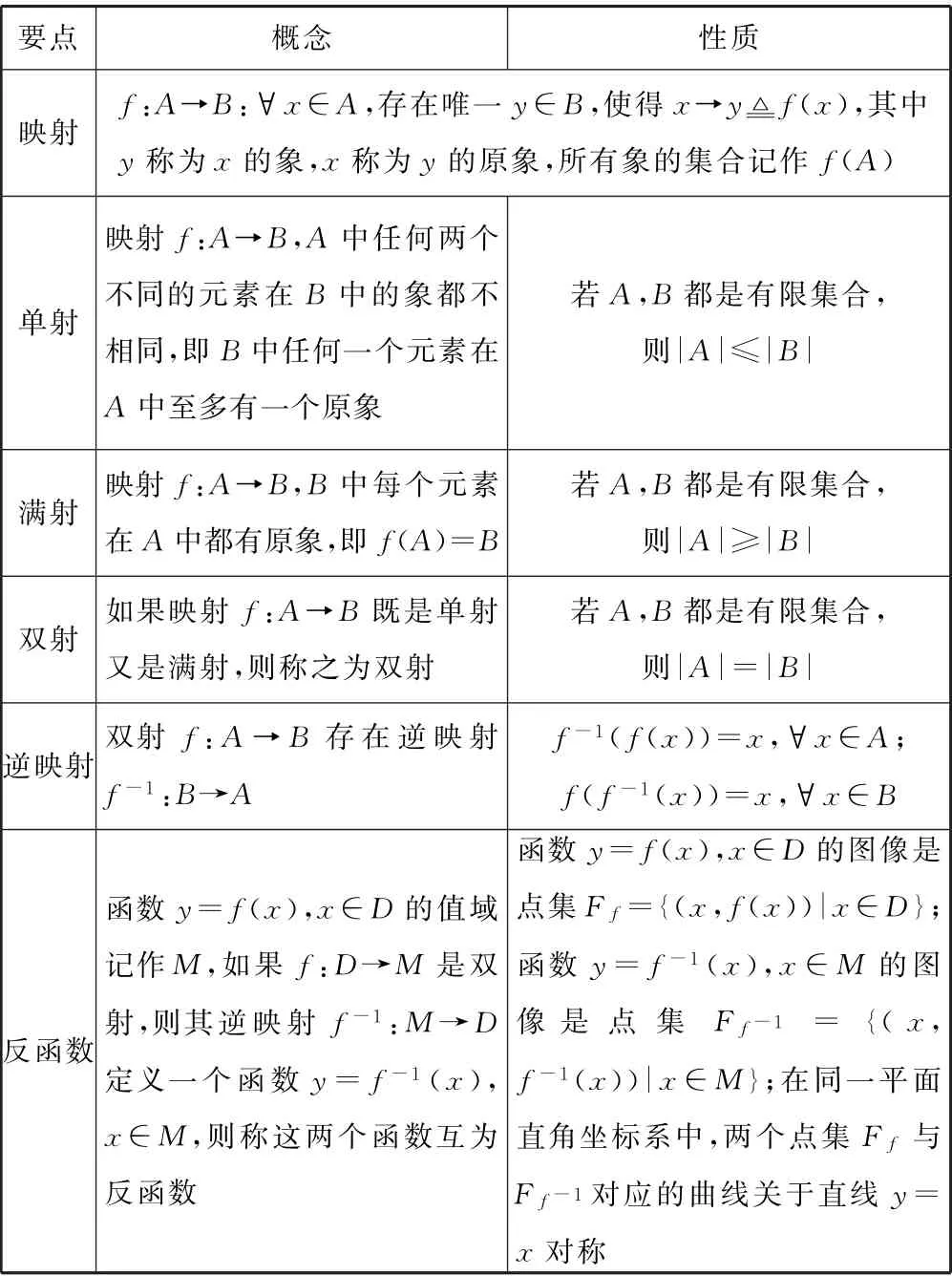
表5

2.11 復合與迭代

表6

2.12 函數方程

(1)函數方程及其解法

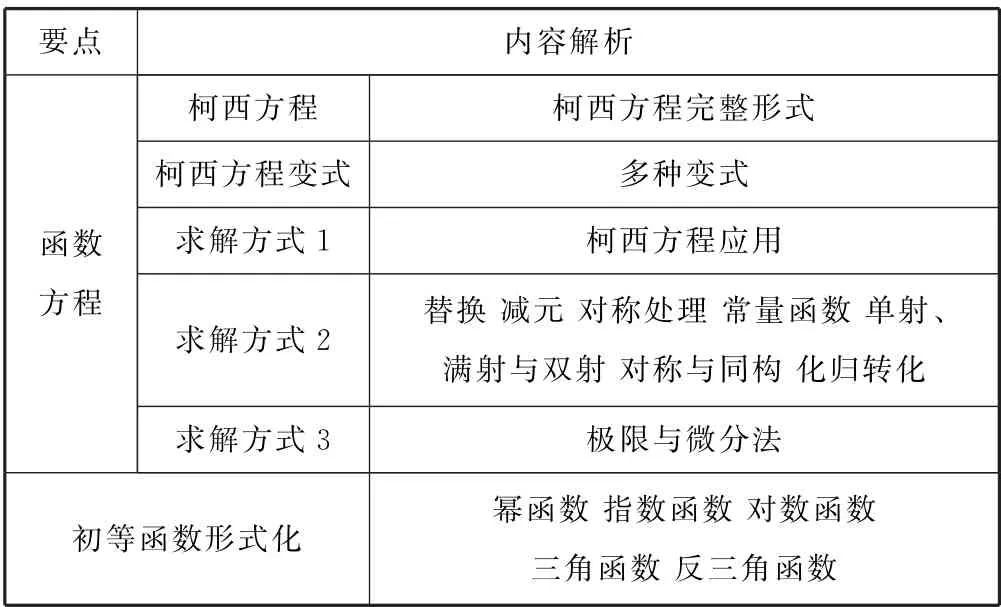
表7

(2)柯西方程

表8

要完整掌握柯西方程,從高校自主招生試題與強基計劃校考出現過的函數方程題目來看,強基命題十分重視柯西方程這個基本模型.這不僅是因為函數方程是函數分析路徑的頂端,即“基本初等函數→初等函數→抽象函數→函數方程→微積分方法→微分方程→……”,另一個重要原因是通過求解函數方程能深刻地培育學生邏輯推理、數學抽象、直觀想象、數學運算、數據分析與數學建模等數學素養.因此,同學們要注重歷練函數方程求解,尤其是柯西方程及其變式.

(3)柯西方程變式

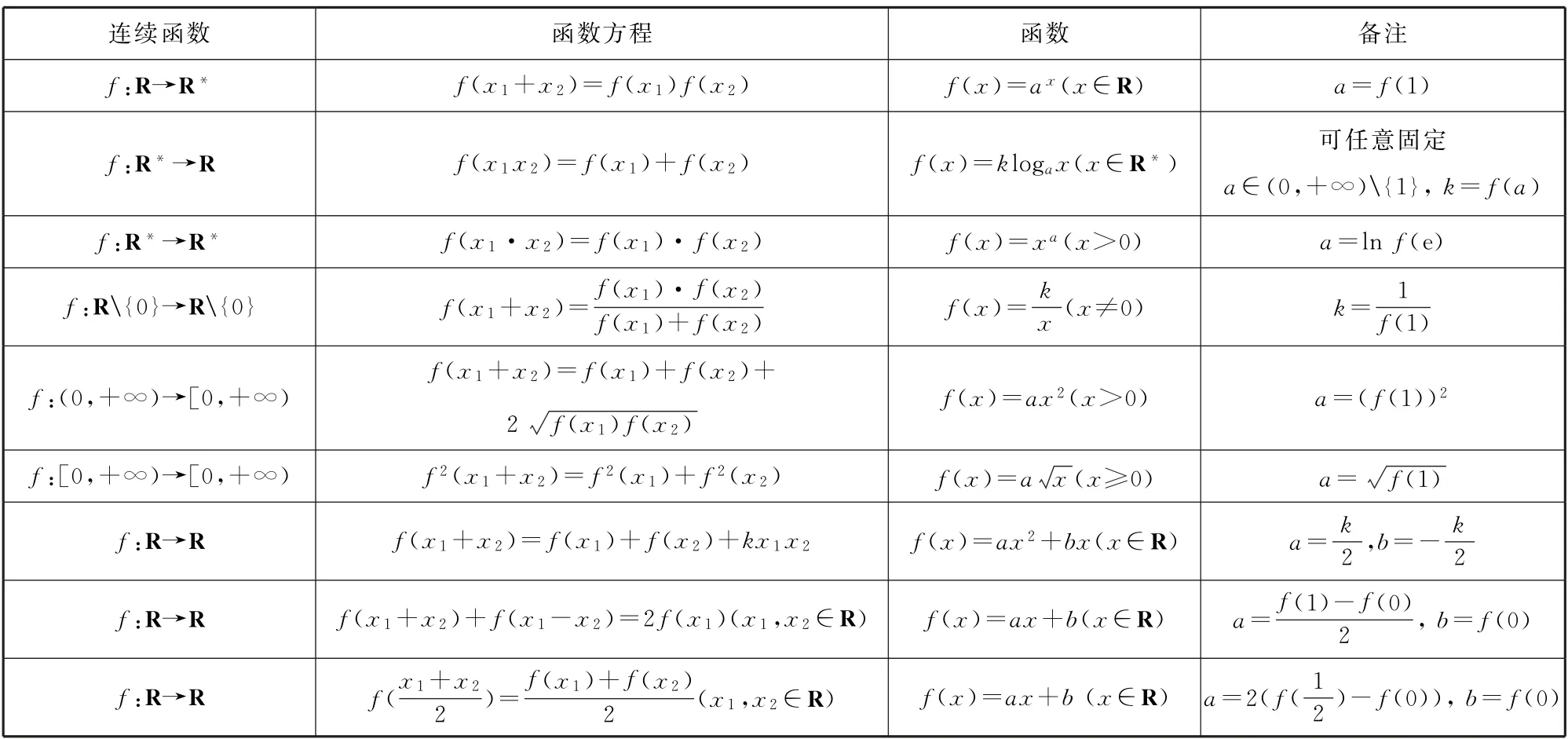
表9

3 典例精析

3.1 集合

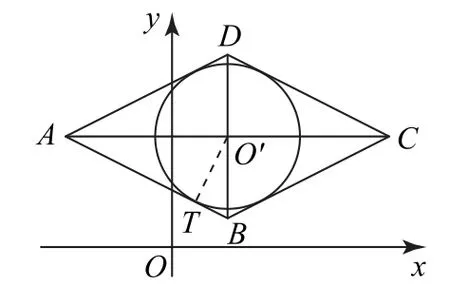
圖1

3.2 邏輯用語

3.3 代數式靈活變形

代數式靈活變形既表現在恒等變形又表現在合理放縮,向著目標調結構.

例6 (清華大學)已知實數a,b滿足a3＋b3＋3ab＝1,其中a＋b取值的集合為M,則( ).

A.M是單元素集

B.M為有限集,但不是單元素集

C.M是無限集,且有下界

D.M是無限集,且無下界

3.4特型方程求解

3.5 定義與三要素

函數的三要素是理解函數、分析函數的性質、論證函數問題的基礎,在各種變式情境中都要準確理解函數三要素.

所以A?B＝AΔB＝(－ ∞,－3]∪[0,1)∪(3,＋∞).

3.6 映射與反函數

高校強基計劃校考試題提示我們,對函數學習的要求務必上升到映射觀點理解函數,清晰理解反函數概念及其雙射基礎,能夠以互為逆映射理解對數恒等式與反三角恒等式,培育抽象素養.

因為f(x)＝3x－3－x是奇函數,所以f－1(x)也是奇函數,從而f－1(4)＋f－1(－4)＝0,故gmax(x)＋gmin(x)＝2.

3.7 函數分析路徑

強基計劃校考試題注重函數分析,取定一個較復雜的初等函數,以不定項選擇題型引領學生分析其性質,試題表現函數分析基本路徑是三要素→基本性質(對稱、單調、周期)→凹凸性→數形結合,建立函數不等式等.

由①③可知,?x∈R,都有f(x)＝f(1－x)＝－f(2a－1＋x)＝－f(2－2a－x)＝f(4a－2＋x),

故函數y＝f(x)是周期函數,周期T＝4a－2≠0,且

3.8 典型函數

強基計劃校考命題十分注重以典型函數及其變式立意試題,既檢測代數變形能力與數學直觀,又檢測函數分析方法.

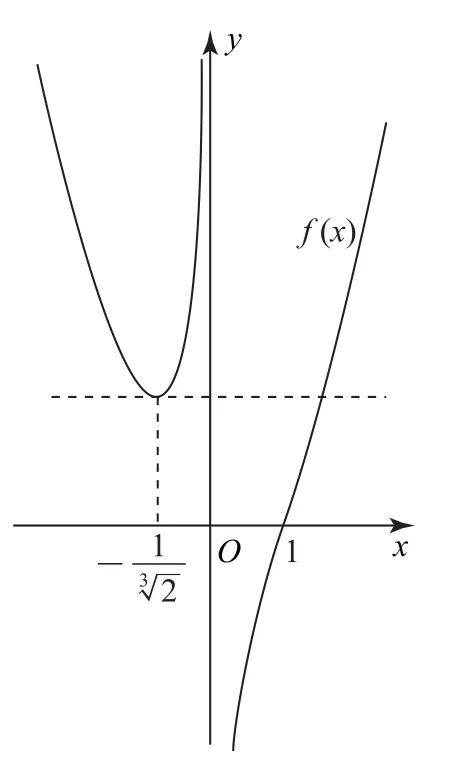
圖2

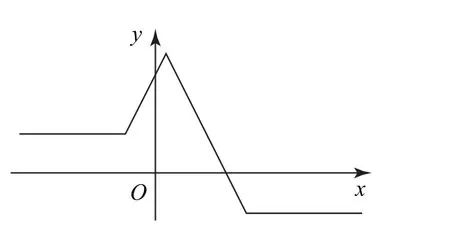
圖3