基于LBP和GLCM的腸道腫瘤圖像特征提取方法

楊 波, 張立娜, 韓霄松

(1. 長春財經學院 信息工程學院, 長春 130122； 2. 吉林農業大學 信息技術學院, 長春 130118；3. 吉林大學 符號計算與知識工程教育部重點實驗室, 長春 130012;4. 吉林大學 計算機科學與技術學院, 長春 130012)

目前針對腸癌的診斷, 醫生通常采用指檢和腸道鏡等方式進行早期排查, 由于腸癌早期癥狀不明顯, 給醫生診斷帶來巨大挑戰. 通過指檢和腸道鏡檢查, 排查早期腸癌的準確率約為80%, 一旦早期診斷出現失誤, 會對癌癥的及時治療和患者心理造成極大影響. 通過對腸鏡和CT圖像進行實時處理, 提取圖像特征輔助腸癌早期識別, 可極大提高診斷效率. 基于此, 本文提出一種基于局部二進制模式(local binary patterns, LBP) 和灰度共生矩陣(gray level co-occurrence matrix, GLCM)的腸道腫瘤圖像特征提取與識別方法, 分割腸道腫瘤的病灶區域, 通過 LBP算法和 GLCM的結合, 判斷腸癌和息肉差異性的同時, 確定適用于腸癌識別分類的特征參數, 進一步提高腸癌早期診斷預測的準確率.

1 腸道腫瘤圖像的感興趣區域

腸道惡性腫瘤通常呈球狀或半球狀凸起, 體積較大, 有的惡性腫瘤伴隨出血、 底部深陷等特點, 也有多個腫瘤集中在一起出現腸腔狹窄的情況. 根據腸道腫瘤的特點, 在對圖像進行特征提取和識別前, 需將腸道腫瘤區域從醫學圖像中進行有效分離, 從而進行更有針對性的研究.

OTSU算法, 即最大類間方差法, 是在判別分析或最小二乘原理基礎上發展而來的[1], 也稱為大津法. 用最大類間方差法可以得到醫學圖像的一個合適閾值, 利用im2bw函數將圖像轉換為二值圖像的過程中, 通常須設置閾值, 該函數能獲得一個較合適的閾值. 該閾值與人工設定閾值相比能得到更好的轉換效果.

利用OTSU算法按照腫瘤圖像灰度的特性, 將腫瘤圖像分割成背景和前景兩部分, 其中前景又稱為目標. 類間方差越大, 表明圖像中的背景和目標之間的差異性越大. 出現誤分情況時, 即存在個別目標被誤分為背景, 或個別背景被誤分為目標, 會使差別變小. 因此, 類間方差最大的分割, 誤分幾率最小. 對于圖像A(x,y), 假設目標與背景的分割閾值為T, 目標像素點數占整個圖像的百分數標記為ω0, 其平均灰度為μ0, 背景像素點數占整個圖像的百分數標記為ω1, 其平均灰度為μ1.該圖像的總平均灰度記為μ, 類間方差記為g, 假設該腫瘤圖像的尺寸為M×N, 圖像中像素的灰度值小于閾值T的像素個數記為N0, 像素灰度大于閾值T的像素個數記為N1, 則有

將μ=ω0×μ0+ω1×μ1代入式(5)可得

g=ω0×ω1(μ0-μ1)2.

(6)

利用遍歷求得使類間方差最大的閾值T.

用OTSU算法得出輸入腫瘤圖像的閾值, 計算最大和最小值, 從最小灰度值到最大值分別計算方差, 計算目標和背景的百分數和平均灰度值. OTSU算法計算前原始圖像如圖1所示, Graythresh函數計算閾值圖像如圖2所示， 簡化OTSU算法計算閾值圖像如圖3所示.

圖1 OTSU算法計算前原始圖像區域Fig.1 Original image area before OTSU algorithm calculation

由圖2可見， Graythresh函數計算閾值圖像腫瘤區域基本被標識為白色區域, 可與背景區域有效區別. 由圖3可見, 簡化后OTSU算法計算閾值圖像與Graythresh函數方法得到的圖像效果相當. 獲得腸癌腫瘤區域輪廓后, 利用drawContours( )函數繪制輪廓并進行區域剪切, 即可得到理想的腫瘤區域圖像. 與計算機視覺開源框架OpenCV自帶算法實驗對比表明, 在分割效果上觀察OTSU算法與OpenCV自帶算法相當, 在計算速度上, OTSU算法時間為0.8 ms, 比OpenCV自帶算法快0.2 ms.

圖2 Graythresh函數計算閾值圖像Fig.2 Threshold image calculated by Graythresh function

圖3 簡化OTSU算法計算閾值圖像Fig.3 Threshold image calculated by simplified OTSU algorithm

2 腸道腫瘤圖像特征提取

2.1 局部二值模式圖像特征

局部二進制模式(LBP)算法一般將一張圖像劃分為中心區和鄰區. 如果30為中心區的像素灰度值, 則將其作為閾值, 此時把圖像中心區獲得的像素值與相鄰8個區獲得的像素值對比[2]. 假設該圖像的中心區獲取像素值大于對比鄰區像素值, 則鄰區可以將對應位置的像素值設定為1, 否則如果鄰區像素值大于中心區值, 則將鄰區對應位置記為0. 以此類推, 將整個標記完的區域從左上角按照順時針讀取8個二進制數, 形成一個二值化后的序列, 其對應的十進制數作為該鄰域中心點的響應. 基本LBP算子的獲取過程如圖4所示.

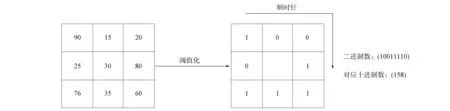
圖4 基本LBP算子的獲取過程Fig.4 Acquisition process of basic LBP operators

LBP算法局部紋理特征計算公式[3]為

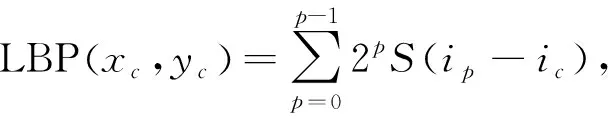
(7)

其中： (xc,yc)為圖像的中心區像素坐標；p為8鄰區中的第p個像素點；ip為p點對應的灰度值；ic為中心區像素對應的灰度值；S(x)為符號函數,

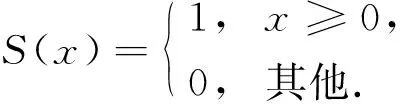
(8)

本文通過實驗將腸道腫瘤圖像的各像素點均通過LBP計算, 獲得的新腫瘤圖像與原腫瘤圖像大小相同, 稱為LBP圖像. 同時計算并繪制腫瘤LBP 圖像的直方圖, 作為描述腫瘤圖像紋理特征的輔助方式[4]. 但基本的LBP算子計算得到的直方圖會出現維數較多的情況, 利用圖像等價模式LBP特征在一定程度上可達到降維的效果.

本文采用LBP算法獲取圖像原始LBP特征, 并顯示其統計直方圖與特征圖像, 腫瘤特征被有效保存, 單腫瘤圖像特征效果如圖5和圖6所示, 多腫瘤圖像特征效果如圖7和圖8所示.

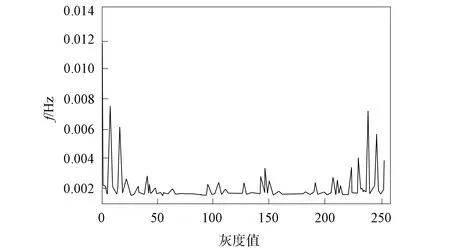
圖5 單腫瘤圖像統計直方圖Fig.5 Statistical histogram of single tumor image

圖6 單腫瘤圖像LBP特征圖Fig.6 LBP characteristic map of single tumor image

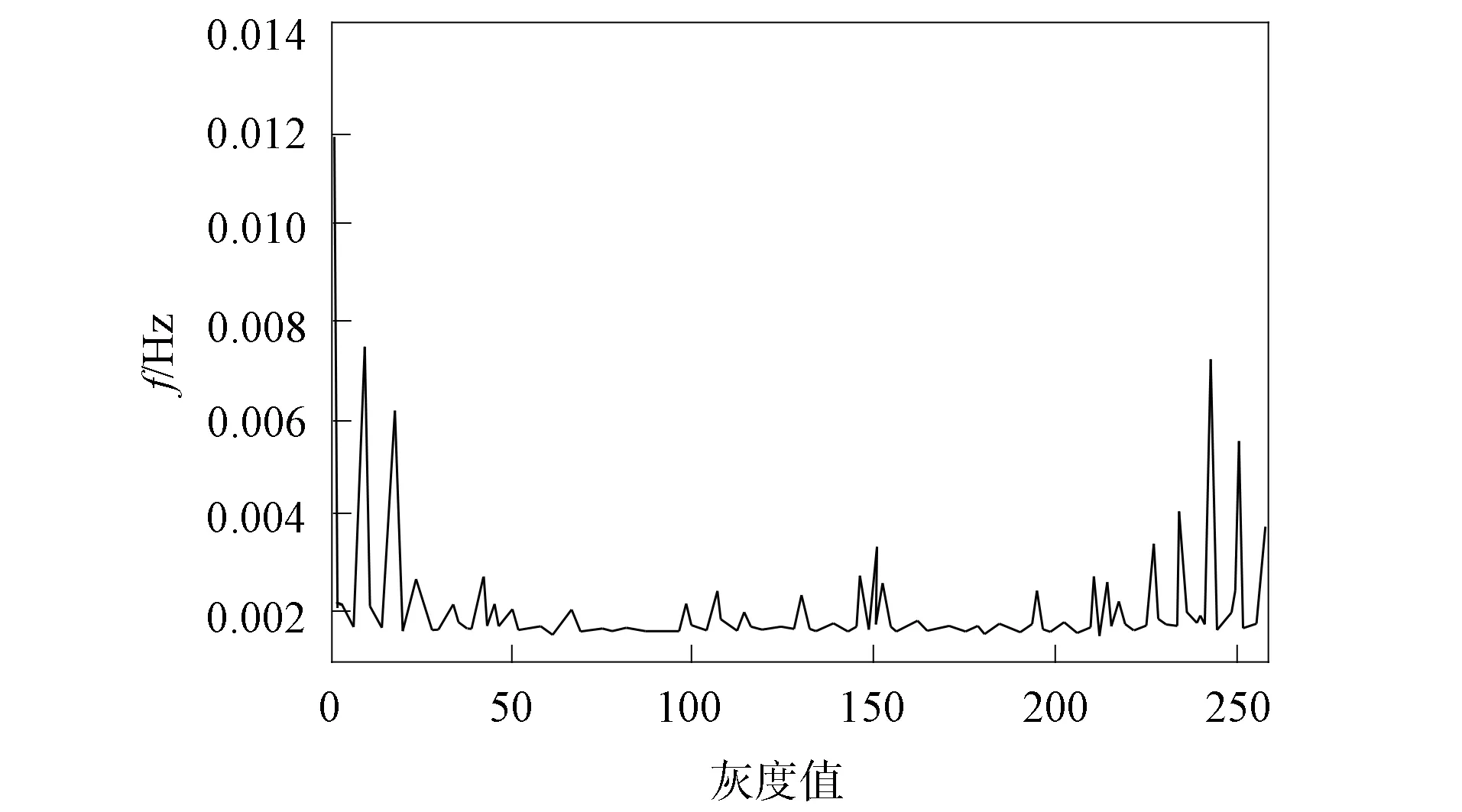
圖7 多腫瘤圖像統計直方圖Fig.7 Statistical histogram of multiple tumor image

圖8 多腫瘤圖像LBP特征圖Fig.8 LBP characteristic map of multiple tumor image

圖9為圖像等價模式直方圖, 圖10為圖像等價模式LBP特征圖. 由圖9和圖10可見, 采用圖像等價模式LBP能表示大多數紋理特征, 同時處理速度得到顯著提高, 有效特征也可以得到較好的保留.

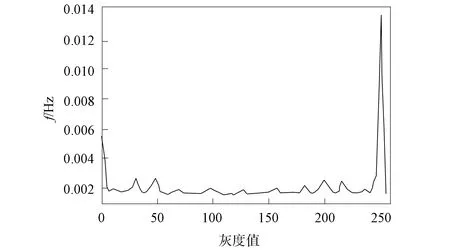
圖9 圖像等價模式統計直方圖Fig.9 Statistical histogram of image equivalent pattern

圖10 圖像等價模式LBP特征圖Fig.10 LBP characteristic map of image equivalent pattern

2.2 灰度共生矩陣

灰度共生矩陣(GLCM)計算兩個點在一定距離和一定方向上的灰度相關性, GLCM反映了圖像在方向、 間隔、 變化范圍和速度等方面的綜合信息[5]. 本文利用GLCM進行全局紋理特征提取, 設腫瘤數字圖像尺寸為M×N, 灰度為K, 為定義腫瘤圖像任意一對像素作為條件的概率密度, 假設預先給定距離d和方向θ(θ為像素對點之間連線與坐標的夾角), 灰度以i為起點, 出現灰度為j的概率.即GLCM是指目標圖像中滿足d和θ成對點灰度出現率, 此概率用P(i,j,d,θ)表示:

P(i,j,d,θ)=([(x,y),(x+m,y+n)|f(x,y)=i,f(x+m,y+n)=j]),

(9)

實際上是(K×K)的矩陣. 圖11為GLCM算法示意圖. 圖11中灰度為i的點坐標為(x,y), 灰度為j的點是偏離灰度為i的另一點, 坐標為(x+m,y+n), (m,n)為偏離值, 則此時將GLCM中相應位置(x,y)處的值加1(初始值為0)[6].

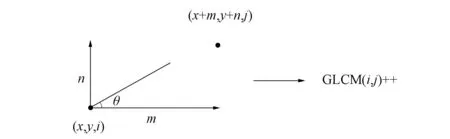
圖11 GLCM算法示意圖Fig.11 Schematic diagram of GLCM algorithm

在實際應用中, GLCM通常不能直接區分紋理特征, 需要一些屬性作為紋理特征的描述, 其中包括14種基于灰度共生矩陣計算出的統計量[7]： 能量(角二階矩)、 熵、 對比度、 均勻性、 相關性、 方差、 和平均、 和方差、 和熵、 差方差、 差平均、 差熵、 相關信息測度以及最大相關系數[8]. 根據需要和實際應用效果, 本文采用角二階矩、 熵、 對比度和反差分矩陣4個統計量. 4個統計量計算方法為

其中： 角二階矩ASM表示腫瘤圖像的灰度分布均勻水平和紋理粗細程度,P(i,j)表示歸一化后的灰度共生矩陣； 熵ENT表示腫瘤圖像包含信息量的隨機性, 同時也反映腫瘤圖像的復雜程度； 對比度CON表示圖像清晰度和腫瘤紋理溝紋深度, 紋理越明顯, 腫瘤圖像中的明暗差距越大； 反差分矩陣IDM又稱為逆方差, 表示腫瘤圖像紋理的清晰水平和規則程度, 該值越大, 表示紋理越清晰[9], 同時越有規律性. 以單個腫瘤為例, GLCM結果如圖12所示.

圖12 GLCM結果Fig.12 GLCM results

將包含單個腫瘤、 多腫瘤和無腫瘤圖像的LBP圖, 根據式(10)～(13)計算獲取GLCM特征值, 對比結果列于表1. 表1中特征值均為單一樣本特征數據. 由表1可見, 多腫瘤圖像的GLCM角二階矩值相對較大, 表示紋理容易描述, GLCM的熵值反映腫瘤圖像相對復雜[10], 對比度較大說明多腫瘤圖像紋理較清晰, 更容易識別.

表1 GLCM腫瘤特征值對比

實際使用過程中, 根據腸道腫瘤醫學圖像的紋理特征, 采用4個方向(0°,45°,90°,135°)生成灰度共生矩陣, 每個方向使用4個統計量標識特征, 生成16個特征值. 再通過計算4個統計量的均值、 標準差和方差, 生成12個特征值, 共28個特征值描述一個腸道腫瘤圖像, 產生的矩陣部分數據列于表2.

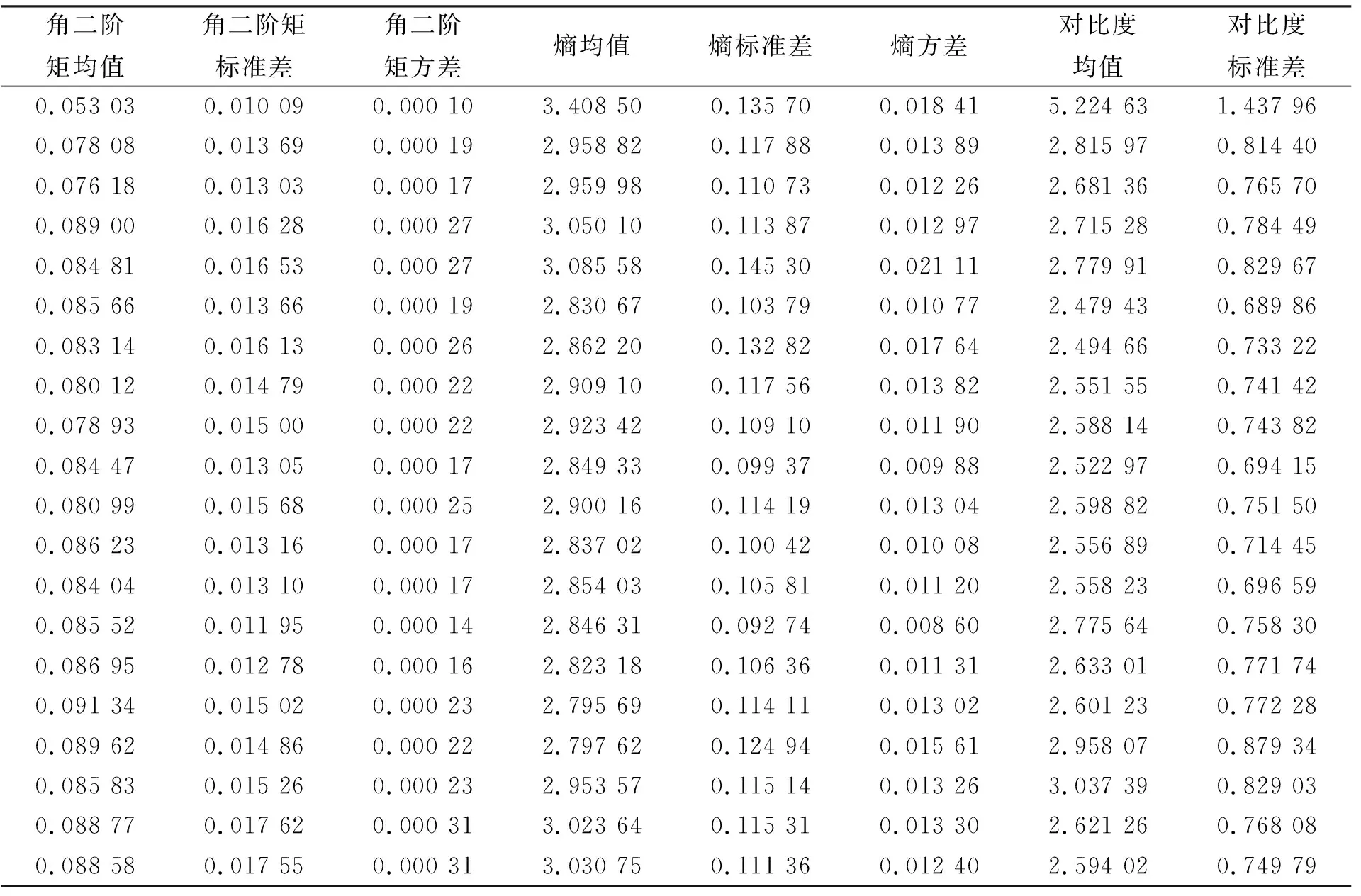
表2 腸道腫瘤圖像GLCM特征

3 實驗結果與分析

本文采用的實驗數據為吉林大學第一醫院二部腸鏡檢查數據圖像, 來自200名患病個體, 圖像信息1 500個. 實驗圖像數據需要臨床醫師進行標定, 腸鏡樣本數據分為單腫瘤、 多腫瘤、 正常腸道和息肉. 臨床醫師根據病例結果對1 500張圖像逐一標定, 最終確定實驗使用的數據集. 其中700張圖像作為訓練數據集, 600張圖像作為測試數據集, 200張圖像作為待測數據集.

支持向量機(support vector machine, SVM)可以在有限樣本信息的情況下, 對模型的復雜性和學習能力之間進行折衷, 獲得較好的推廣能力和識別效果[11]. 針對SVM識別方法, 本文采用LBP+SVM,GLCM+SVM和LBP+GLCM+SVM三種方式進行分類識別. SVM可采用多種核函數, 其中參數γ和誤差懲罰因子C是核函數的主要參數, 本文利用交叉對比法.

SVM通過用內積函數定義的非線性變換將輸入空間變換到一個高維空間[12]. SVM核函數K(xi,xj)是輸入空間和特征空間之間的映射.

多項式核函數表示為

(14)

徑向基核函數(RBF)表示為

K(xi,xj)=exp{-γ‖xi-xj‖2},

(15)

其中d為多項式次數,γ為模型復雜度系數. 通過核函數的使用, SVM將二維線性不可分樣本映射到高維空間中[13]. 樣本數據在高維空間中變得線性可分.

針對腸道腫瘤樣本數據, 本文測試了SVM兩種核函數的識別準確率, 結果表明, 多項式函數當多項式次數達到一定值時精度開始下降, 次數D=4時達到最高.RBF核函數精度普遍高于多項式函數, 當C=26,γ=0.3時, 精度達到最高. 本文選擇深度學習的VGG模型作為對比實驗, 該模型相比傳統卷積神經網絡更適合樣本數較少的識別任務[14]. 在樣本集上， VGG19模型的損失值結果如圖13所示, 準確率結果如圖14所示. 不同方法實驗對比結果列于表3.

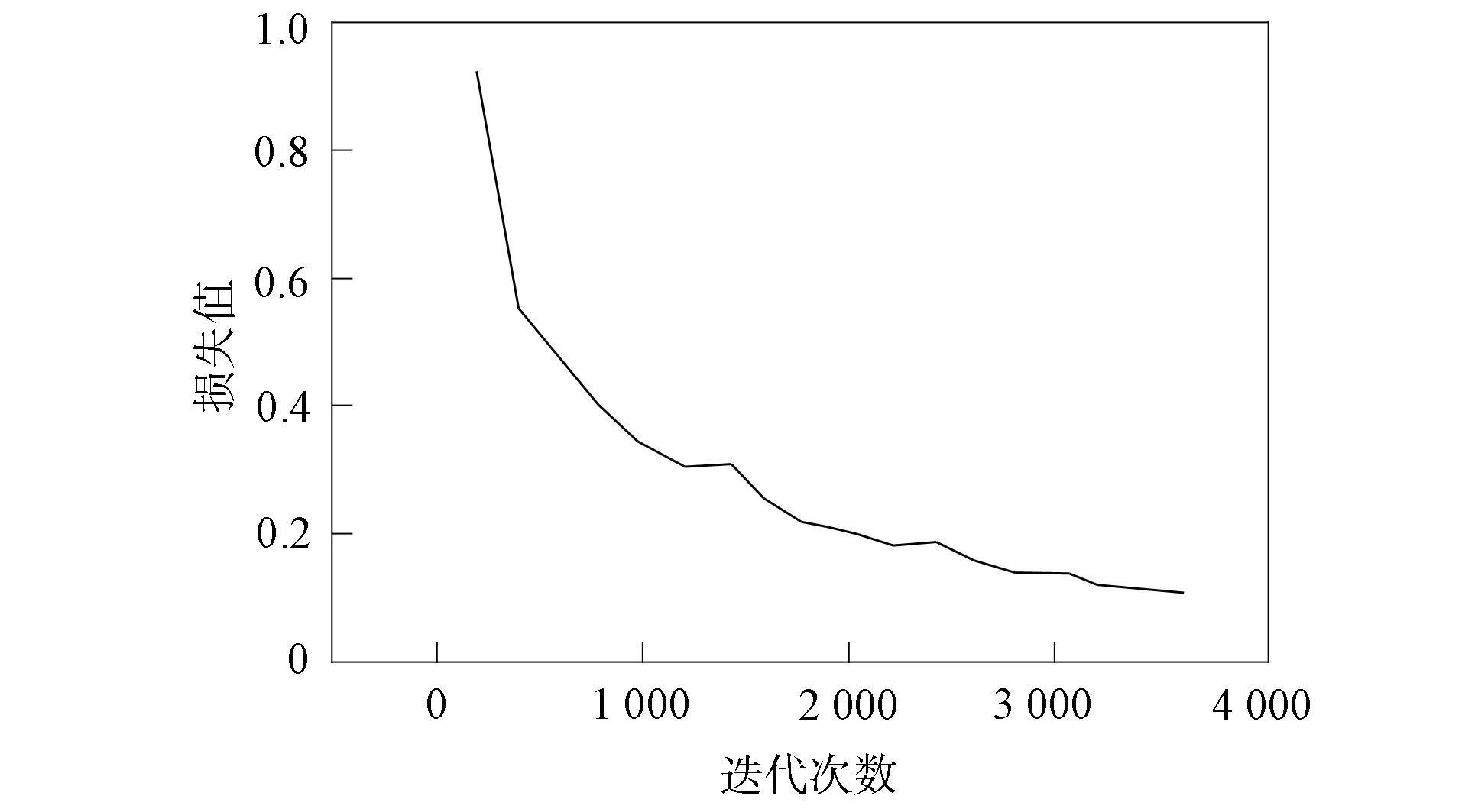
圖13 樣本集上VGG19的損失值Fig.13 Loss values of VGG19 on sample set

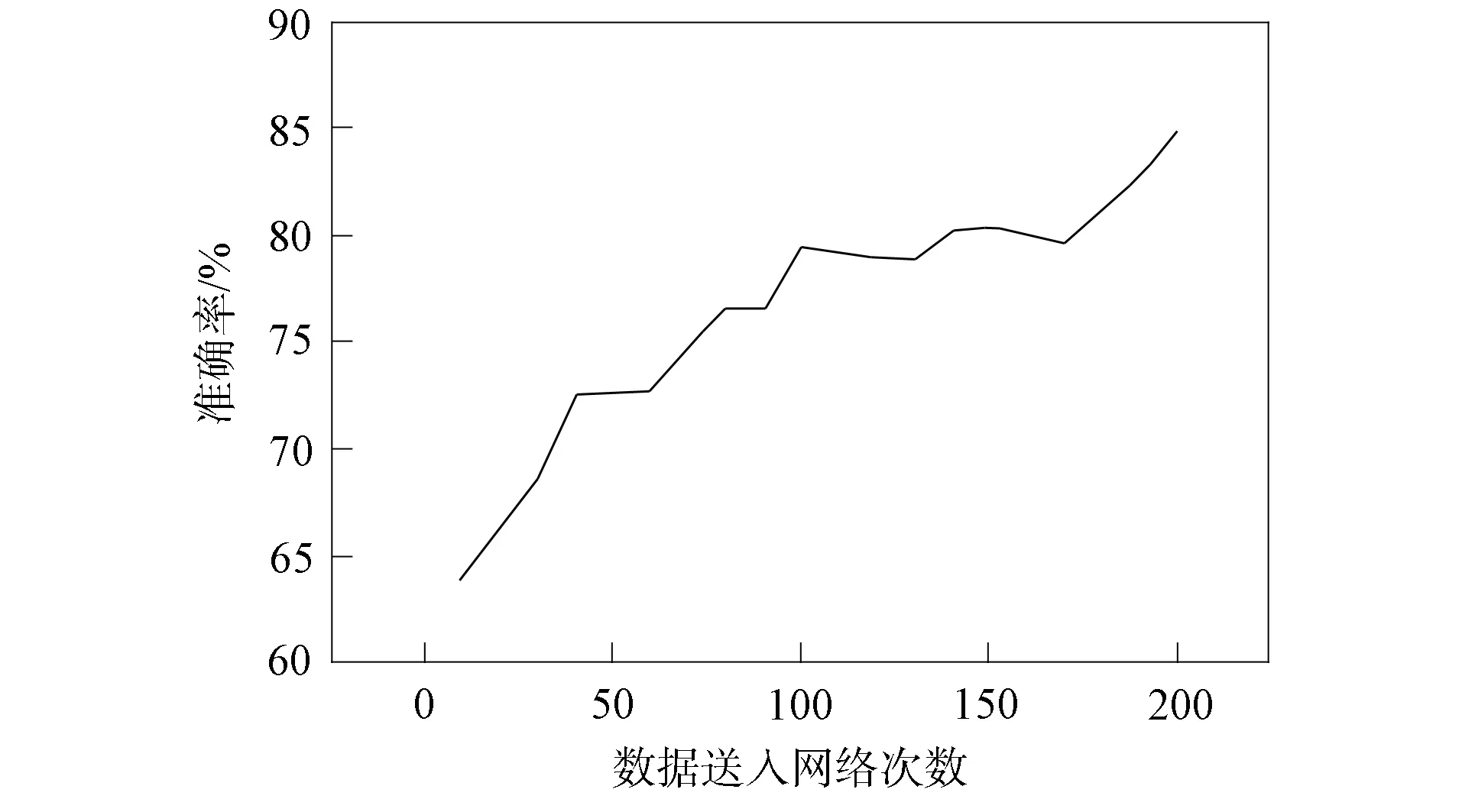
圖14 樣本集上VGG19的驗證準確率Fig.14 Verification accuracy of VGG19 on sample set

表3 不同方法的實驗結果對比

由表3可見, 直接采用LBP模式圖像特征提取方法對腸道腫瘤醫學圖像進行識別分類的準確率為85.66%, 局部紋理特征提取后進行SVM識別效果不明顯. 采用GLCM獲取全局紋理特征提取法識別效果稍好, 準確率提高了4%. 采用LBP+GLCM+SVM方法, 準確率達到94.84%. VGG19模型經過訓練, 當損失值為0.162 4時, 損失值曲線趨于平穩, 此時準確率穩定在約84.68%, 隨著epochs訓練迭代次數的增加, 準確率未出現明顯變化.

綜上所述, 針對腸道腫瘤圖像樣本有限導致腫瘤識別率低和收斂速度慢的問題, 本文提出了一種LBP+GLCM+SVM方法. 利用GLCM方法對腸道腫瘤圖像進行全局特征紋理獲取, 彌補了LBP方法缺少中心區像素點灰度計算的缺陷, 并結合了LBP高效性和GLCM魯棒性的優點. 深度學習VGG模型方法由于卷積神經網絡在訓練時, 為保證訓練不被過擬合, 需要大量的訓練數據, 使得VGG方法樣本數量要遠大于SVM方法, 且訓練速度較慢. 實驗結果表明, SVM方法較適用于小樣本數據的情形, 同時LBP+GLCM+SVM方法分類精度為94.84%, 優于VGG19方法的84.68%, 取得了較理想的識別準確率, 可實現輔助腸道腫瘤醫學診斷的目的.