離心風機葉型安裝角βb(r)徑向分布的氣動作用研究

劉少林，楊愛玲，陳二云

（上海理工大學 能源與動力工程學院，上海 200093）

在離心通風機葉輪的設計過程中一般依據經驗和公式確定葉輪進出口半徑、安裝角等參數。而葉片徑向加載規律即葉型往往較簡單，多采用單圓弧或雙圓弧葉型。這是因為旋轉葉輪內部流動情況較復雜，很難在設計時就確定精細、高效的葉片造型。然而，相關研究表明葉片型線對于離心風機的性能和流場品質有較大影響。

可控渦設計方法是對離心壓縮機或透平等離心葉輪反問題求解的一種方法。該方法通過控制葉輪內環量沿半徑方向的變化，獲得物理量在流道內的合理分布。在可控渦設計方法中合理的環量分布是關鍵。祝啟鵬等針對離心壓氣機并通過貝塞爾曲線擬合優化環量分布；易喆鑫等將離心風機進、出口參數與葉片型線的設計相配合，得到了較合理的葉型設計；張莉等通過求解雙調和方程并考慮了一定的氣動條件，給出了一種確定環量分布的方法。上述研究均是在無黏和無限多葉片等假設下進行優化設計，然后考察流動是否得到改善，然而實際流動葉片是有限的，且黏性對流場品質的影響不能忽略。本文基于數值模擬方法，研究離心風機葉型安裝角β()徑向分布對流動物理參數的影響，為實現葉片流道內流動的精細控制提供依據。

1 葉輪模型

圖1為某型后彎式離心風機葉輪幾何參數示意圖。該離心風機全壓 Δ為 1 200 Pa，流量為4 000 m·h，轉速為2 900 r·min，葉片數為19，采用3.0 mm 的等厚葉片。圖1 中：、分 別為葉輪進、出口寬度； β、 β分別為葉片進、出口安裝角；M、L 為流場觀測點；β()表示葉型曲線切線與圓周方向夾角，即葉型安裝角，表示半徑；為相對速度流線弧長； ω為葉輪旋轉角速度；、分別為葉輪進、出口半徑，不同葉高處（相對于出口寬度）半徑的取值如表1 所示。根據通風機原理，任意半徑處單位體積流體獲得的理論功率為

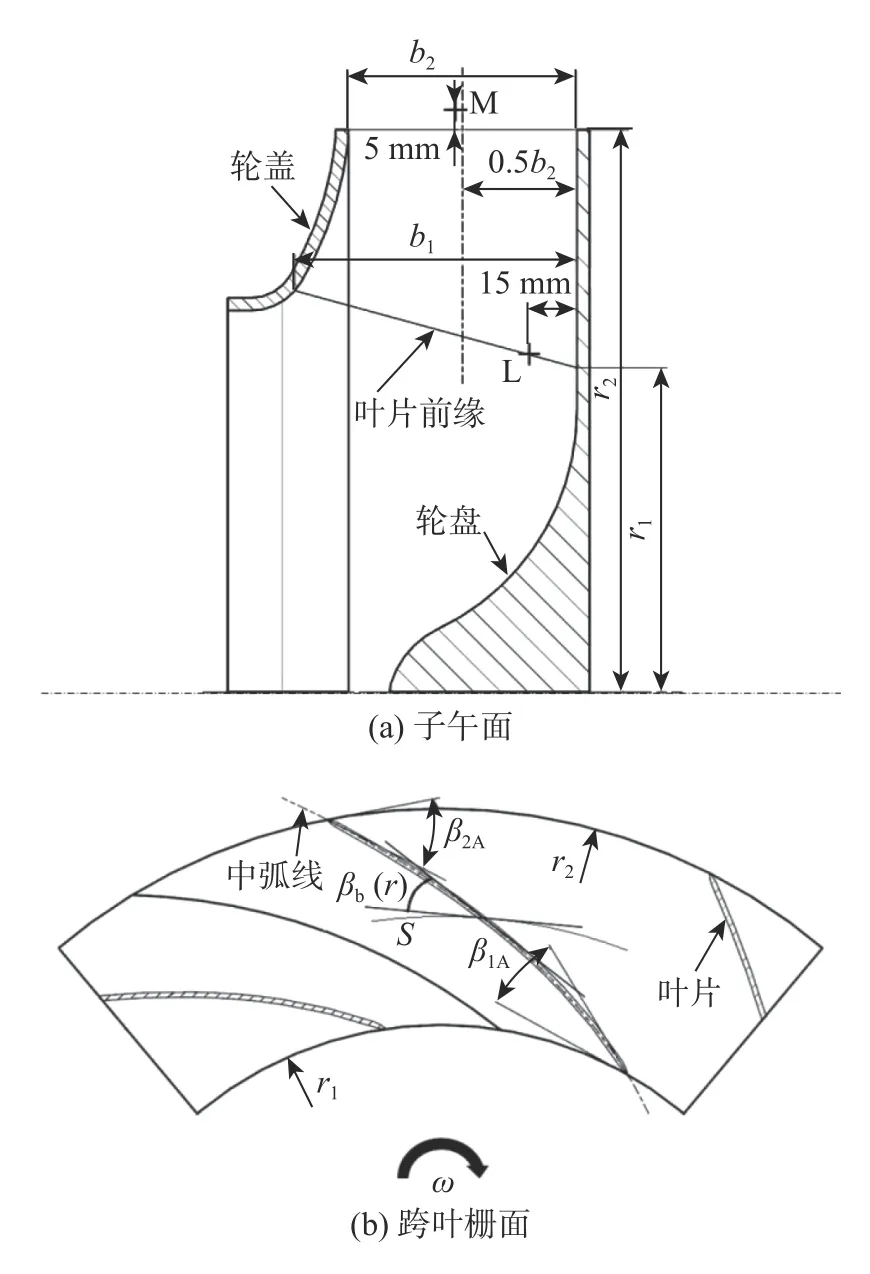
圖1 葉輪幾何參數示意圖Fig. 1 Geometric parameters of the impeller

表1 葉輪進、出口參數Tab. 1 Parameters of the impeller at the inlet and outlet

式中： ρ為空氣密度；、、分別表示絕對速度 →、相對速度→和 圓周速度 →的 大 小；、分別為→在徑向、周向的分量；為→在周向的分量；、分 別為、在葉輪進口處的值。

可見，在葉輪幾何結構參數確定的情況下，β()確定了葉片做功沿徑向的變化，同時也決定了葉輪流道內流動物理參數沿流向的分布。

圖2給出了本文研究的3 種葉型安裝角β()分布，其中：葉型1 表示單圓弧葉型，該葉型簡單且易于制造，因此被廣泛采用；葉型2 選取文獻［13］中性能較好，中間圓系數及葉片角系數分別為0.7、0.3 的雙圓弧葉型；為簡單起見，葉型3 選取葉型安裝角隨半徑線性變化的葉型，以便進行對比、分析。圖2 中橫坐標指無量綱化后的相對半徑，即

圖2 葉型安裝角隨相對半徑的變化Fig. 2 Evolution of blade mounting angles with the relative radius

可見，葉型1 的 β()隨半徑先快速增加后平緩增加，葉型2 的 β()則與之相反，葉型3 的則均勻線性增加。圖3 給出了按式（1）計算得到的與3 種葉型β()相對應的功率加載曲線，縱坐標表示流體沿葉型曲線切線方向流動時計算得到的加載功率與葉型曲線終點處加載功率之比。可見，3 種葉型功率加載曲線與葉型安裝角的變化趨勢基本一致。在滿足設計要求情況下，葉型安裝角的大小決定了加載功率的大小。

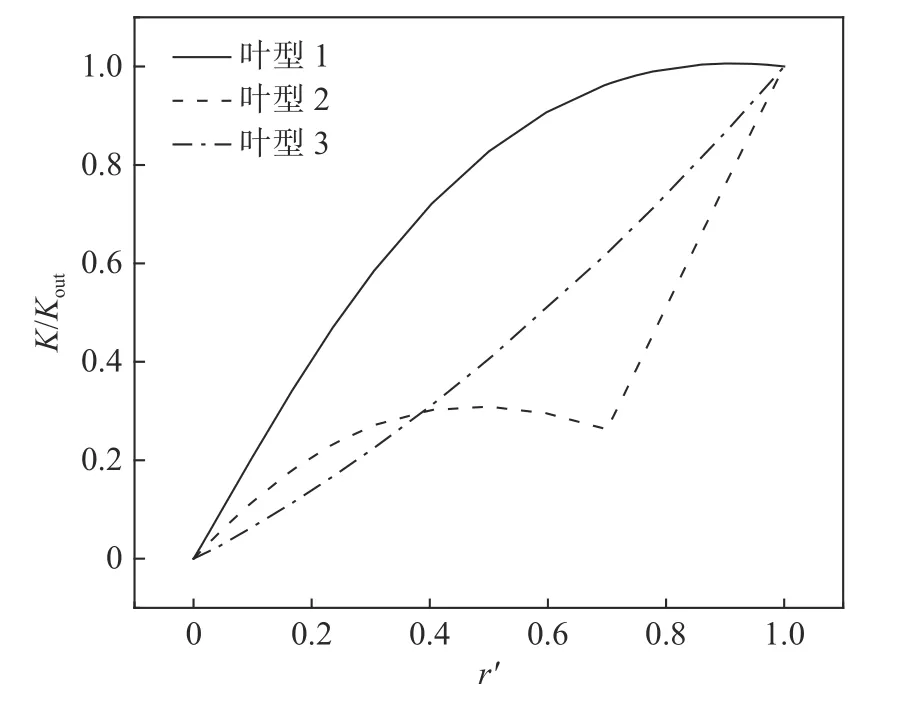
圖3 功率加載隨相對半徑的變化Fig. 3 Evolution of power loading with the relativeradius

2 數值模擬方法

2.1 流動控制方程及湍流模型

本文采用雷諾平均的N-S 方程作為流動控制方程，即

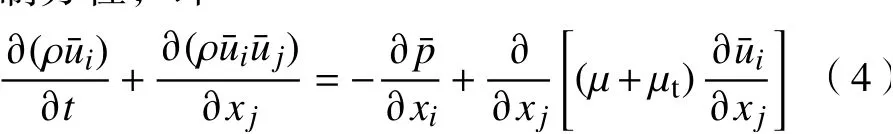
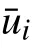
為封閉上述控制方程，采用RNG-湍流模型計算湍流黏性系數。該湍流模型能更好地模擬高應變率和流線彎曲程度較大的流動，其方程基本形式為

本文采用Ansys CFD 軟件提供的二階精度壓力速度耦合Simplec 算法求解上述控制方程。

2.2 計算域及網格

圖4為離心風機流場計算域及網格示意圖。流場計算域分為5 個子域，分別為進口延長段、集流器、葉輪域、蝸殼域和出口延長段，如圖4（a）所示。其中，進口延長段長約為離心風機進口直徑的5 倍，出口延長段約為蝸殼出口寬度的6 倍。

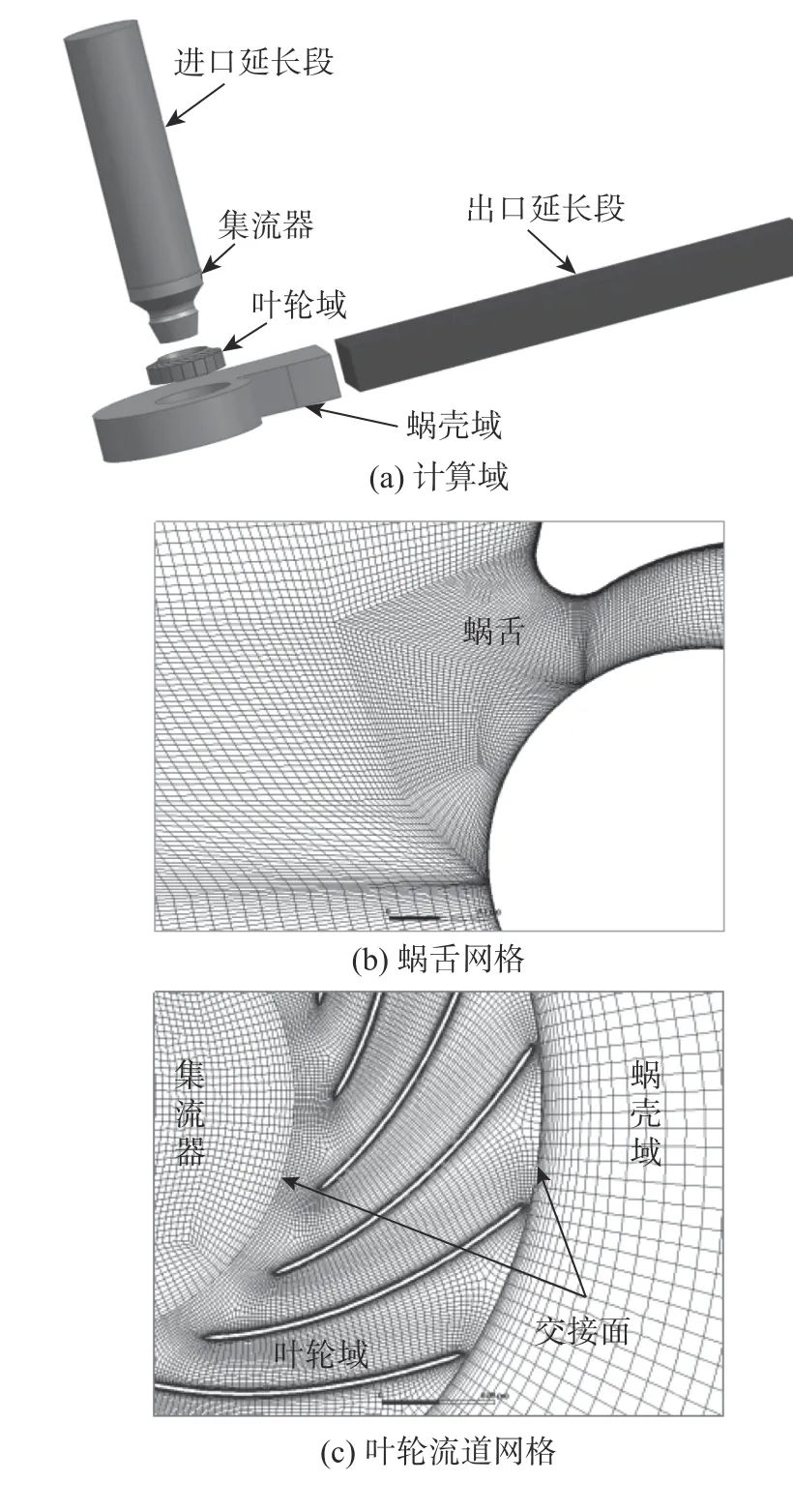
圖4 離心風機流場計算域及網格示意圖Fig. 4 Schematic diagram of the calculation domain and the flow channel grid of the centrifugal fan

對各計算子域均采用六面體結構網格進行空間離散。除蝸殼上、下表面外，所有壁面邊界層區域第一層網格厚度約為0.01 mm。離心風機整體網格數量在850 萬～890 萬之間，葉輪單個流道網格數量約23 萬。圖4（b）、（c）分別為蝸舌和葉輪流道網格示意圖。在ICEM 軟件中檢查其綜合質量（Quality 項），最小值為0.313。定常計算結果顯示，葉輪壁面區域（第一層網格厚度與摩擦速度的乘積與空氣的運動黏度之比）在1～3.5 之間。

計算域涉及進口、出口和無滑移三類邊界條件。本文進口給定來流速度，出口采用自由出流條件。

3 風機流場及性能

圖5為設計工況下3 種葉輪出口監測點M 的 靜 壓周 向 分 布。 監 測 點M[參 見圖1（a）]位于葉輪出口50%葉高平面，距離葉輪出口5 mm 處，沿周向共均勻布置了37 個觀測點。從圖5 中可以看出，3 種葉輪模型靜壓周向分布基本相似：在90°位置時靜壓開始增大，在即將到達蝸舌位置（210°～240°，葉輪順時針旋轉）時靜壓又恢復到原來的水平。圖5 中的周向靜壓分布意味著葉型β()對葉輪出口參數周向分布影響較小。

圖5 設計工況下葉輪出口靜壓周向分布Fig. 5 Circumferential distribution of static pressure at the impeller outlet under design conditions

為了觀察葉輪內部流動參數沿半徑的分布情況，在每種葉輪流道內相同位置作一條流線，如圖6 所示。流線的起點L[參見圖1（a）]位于葉輪前緣，1/2 柵距位置且離輪盤面15 mm 處。圖7 為3 種葉型在設計工況下沿19 條流線的靜壓系數 ξ分布， ξ=/[ρ(ω)]。圖中：虛線是沿19 條流線的靜壓系數分布；實線為19 條靜壓系數曲線的平均值，該平均值反映了葉輪內靜壓系數整體的變化情況。由圖7 中可見，各模型的靜壓系數在不同流道內沿流向的變化趨勢基本一致。對比圖7 可知，β()對靜壓系數的大小和徑向分布均有一定影響。下文為方便起見均取圖6 中流線上物理量的平均值進行對比分析。

圖6 設計工況下葉輪內部待考察流線位置Fig. 6 Positions of the streamlines to be investigated in the impeller under design conditions

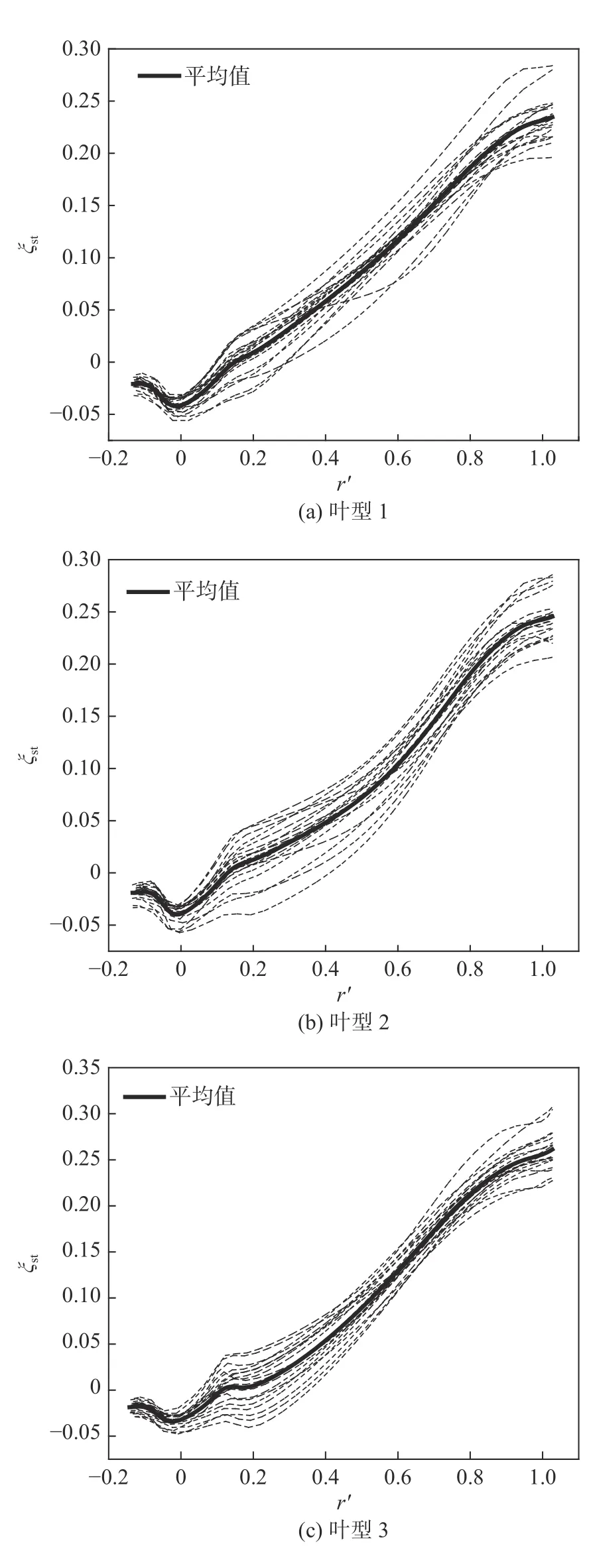
圖7 設計工況下葉輪內部靜壓系數分布Fig. 7 Distribution of static pressure coefficient in the impeller under design conditions

圖8為流線幾何參數，其中：→、 →分別為葉輪流道內流線在某半徑處的切向和法向單位向量； θ為半徑方向與軸的夾角； α為流線切線與軸的夾角； β為相對氣流角，定義為→與當地圓周速度反向的夾角。

圖8 流線幾何參數Fig. 8 Geometric parameters of the streamline

圖9給出了設計工況下離心風機流道內相對氣流角均值沿流向的分布。可見，氣流角與葉型安裝角徑向分布有較大差別，且氣流角明顯小于葉型安裝角。在葉片進口存在氣流正沖角，葉型1、2 和3 的沖角分別為1.9°、3.3°、4.6°。在流道進口段和出口段僅有一個葉型面發生作用，氣流跟隨性較差，故氣流角與葉型安裝角相差較大。當 0 .2 ＜＜0.6時，葉型1、2 和3 的葉輪流道內氣流角沿徑向的分布與葉型安裝角徑向分布幾乎平行，且近似線性分布。這是因為流體受到相鄰葉型面的約束作用，保持了較好的跟隨性。

圖9 設計工況下相對氣流角均值沿流向的分布Fig. 9 Distribution of mean value of relative flow anglealong the flow direction under design conditions

圖10為3 種葉輪離心風機外特性曲線，圖中：橫坐標為體積流量與 額定體積流量之比； η為全壓效率。從圖10（a）中可知，在葉片進、出口半徑和安裝角不變時，3 種 β()分布的風機全壓并不相等，在設計工況下，全壓的差別在 ± 2%左右，特別是在大流量工況下，葉型3 的全壓明顯高于其他兩種葉型。由圖10（b）中可知， β()分布對風機氣動效率的影響更為明顯，葉型1 分布的全壓效率相對較低，葉型3 分布的全壓效率要優于葉型1、2，尤其是在大流量范圍能保持較高的全壓和全壓效率，說明該葉型安裝角分布更適合大流量工況。對比圖9 中葉型3 的 β與其他葉型的主要不同之處是出口附近減小得較慢。在這種變化趨勢下，隨著流量增大，葉型3 的全壓可能下降得較慢，從而更適合大流量工況。

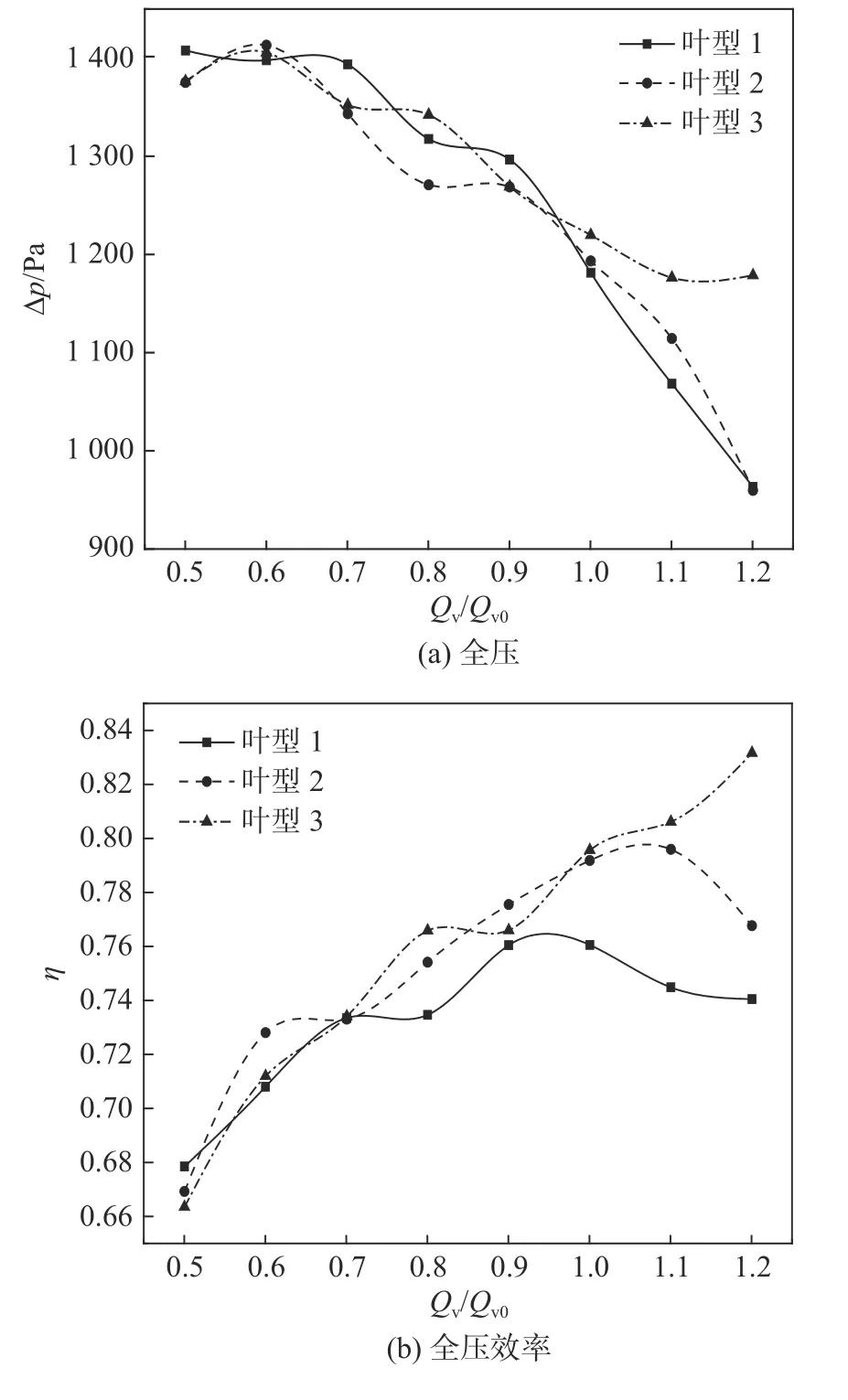
圖10 3 種葉輪風機特性曲線Fig. 10 Characteristic curves of the fans with three kinds of the impellers

圖11為設計工況下葉輪70%葉高截面渦量云圖，圖中黑色圓弧處于=0.6位置。由圖11可見，葉型1～3 截面渦流分布范圍逐漸減小，整體上葉片吸力面分離點逐漸靠近出口，邊界層分離被延遲。可以推測出葉輪內旋渦流動的劇烈程度應逐漸減弱，這可能是導致設計工況下葉型1～3 全壓效率逐漸升高的一個原因。

圖11 設計工況下葉輪70%葉高界面渦量云圖Fig. 11 Contour of the vorticity at 70% blade height under design conditions

4 葉輪流道內流體受力分析

設葉輪流道內單位質量流體受到的力和慣性力分別為、。根據文獻［15］，兩者之間具有以下關系，即

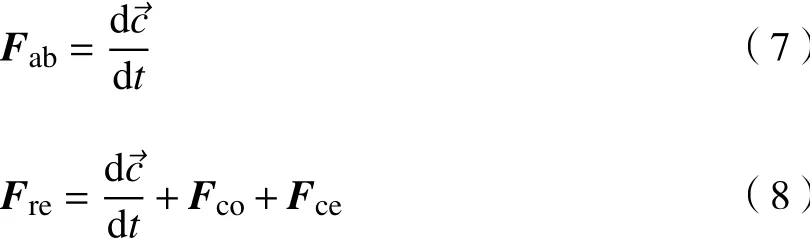
式中：為 哥氏慣性力；為離心力。

在旋轉非慣性系中，慣性力沿流線法向的分量若為正，則表示該分量指向吸力面（如圖8 所示），有利于控制葉片吸力面附面層的增長和分離，反之，背離吸力面，可能加劇附面層分離趨勢。圖12 為設計工況下葉型1 葉輪各力流線法向分量沿流向的分布，下標 n 表示相對速度流線法向。、變化趨勢近似，波動幅度較大，它們受葉型影響也較大。因此，為抑制葉片表面尤其是尾緣附近吸力面附面層的增長、分離，應盡可能控制的大小。

圖12 設計工況各力流線法向分量平均值沿流向分布Fig. 12 Distribution of average normal component of each force along the flow direction under design conditions (line 1)

離心力流線法向分量

由式（9）可知，哥氏慣性力流線法向分量（σ為角速度矢量與相對速度矢量夾角，近似為90°）

圖13 絕對速度與流線幾何量的關系Fig. 13 Relationship between absolute velocity and geometric quantity of the streamline

圖14 設計工況下慣性力流線法向分量平均值沿流向分布Fig. 14 Distribution of average normal component of inertial force along the flow direction under design conditions

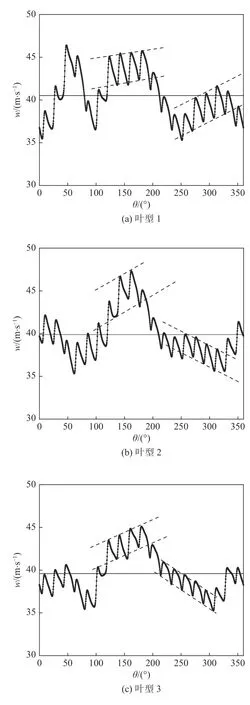
圖15 設計工況下葉輪進口處50%葉高相對速度周向分布Fig. 15 Circumferential distribution of relative velocity at 50% blade height of the impeller inlet under design conditions

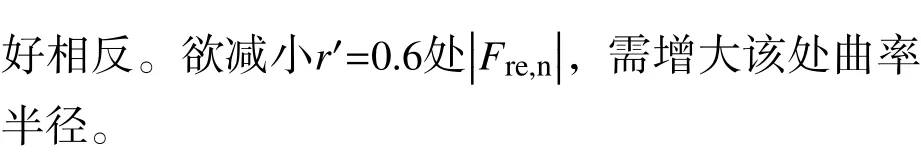
圖16 設計工況曲率半徑平均值沿流向分布Fig. 16 Distribution of average curvature radius along the flow direction under design conditions

5 結論與展望

對3 種葉型離心風機進行了穩態數值模擬，選擇靠近輪盤的流線進行分析，得到以下結論：

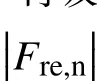
（2）慣性力在流線法向的分量會影響吸力面于削弱附面層分離趨勢。

（3）為實現后加載應當在出口位置盡量增大流線曲率，同時也能減小慣性力法向分量的大小。