綜合斜率和三次樣條的EMD端點效應抑制方法

梁黎明， 王茂芝， 徐文皙， 譚夢婷， 張明月， 王尚坤

(1. 成都理工大學 數(shù)理學院，成都 610059; 2. 成都理工大學 數(shù)學地質四川省重點實驗室，成都 610059)

自從Huang等[1-2]于1998年提出經(jīng)驗模態(tài)分解方法(empirical mode decomposition, EMD)以來，該方法被廣泛應用于各學科領域非線性非平穩(wěn)信號處理。EMD將信號分解為頻率由高到低的本征模態(tài)函數(shù)(intrinsic mode function, IMF)，是一種完全自適應的信號分析方法。然而，EMD在提取IMF時，依據(jù)信號局部極值點構建其上、下包絡線，而信號端點通常不是極值點，進而需要借助端點延拓才能使包絡線覆蓋信號并進行后續(xù)操作。不良的端點延拓會導致包絡線兩端的誤差放大，進而在所提取的IMF分量中 (特別是在IMF的兩端) 出現(xiàn)虛假成分，并且這些虛假成分逐漸向內“傳播”，最終造成信號分解結果失真，產(chǎn)生所謂的端點效應。當輸入信號較短、頻率較小時，端點效應更為明顯，進而導致所提取的IMF失去物理意義。因此，抑制和消除端點效應是EMD應用的重要前提，受到學者的廣泛關注。

已有研究表明，抑制EMD端點效應的端點延拓算法設計主要從增加信號兩端極值點來實現(xiàn)延拓包絡線的目的。如：Rilling等[3]提出的鏡像法以信號兩端的第一個極值點為邊界，把信號向外映射，通過獲取原信號的鏡像得到一個覆蓋原信號的包絡曲線；王紅軍等[4]提出改進的多項式擬合法，利用端點處的三個極值點進行多項式擬合，將計算值作為延拓點的近似取值；Huang等[5]提出極值法，以端點的一個特征波為依據(jù)，在兩端各延拓兩個極大值點和極小值點；Datig等[6]提出斜率法；Wu等[7]在Datig等的基礎上提出改進的斜率方法(improved slope based method, ISBM)，根據(jù)信號端點相鄰極值點求得斜率，利用端點的第一個極值點和斜率確定延拓點所在的線性方程，以此確定延拓點的位置；Xu等[8]提出基于三次樣條的延拓算法(cubic spline based method, CSBM)，利用延拓后的包絡線必須覆蓋原包絡線的限制，確定信號兩端局部極值點與延拓點之間的關系，得到滿足條件的延拓點。此外，還有利用Lyapunov指數(shù)預測模型[9]和波形特征[10]來預測延拓點，以及采用其他類型的樣條函數(shù)[11-12]擬合包絡線進行延拓。

CSBM由于較好地控制了延拓包絡線和原始包絡線在共同區(qū)域內保持一致的特性，具有良好性能。但同時，CSBM在確定延拓點坐標位置時依靠文中提出的兩個準則及包絡線來確定，缺乏對信號趨勢的考量。另一方面，ISBM在延拓點位置的確定上，利用斜率來刻畫信號局部趨勢。本文提出一種基于斜率和三次樣條相結合的端點延拓方法(slope and cubic spline based method, S-CBM)，該方法綜合了ISBM和CSBM的優(yōu)勢，能有效抑制端點效應對EMD分解結果的影響。

1 EMD算法

與傅里葉變換和小波變換等傳統(tǒng)方法相比，EMD是一種新型的時間序列分析方法。該方法依據(jù)數(shù)據(jù)自身時間尺度特征進行信號分解，無須預設基函數(shù)，克服了傳統(tǒng)時頻分析方法需要確定基函數(shù)的局限性。理論上，EMD可以應用于任何類型的信號處理，特別在處理非平穩(wěn)非線性數(shù)據(jù)上具有明顯優(yōu)勢。通過EMD篩選出來的IMF需滿足兩個準則：一是上包絡線和下包絡線均值為零；二是極值點個數(shù)與過零點個數(shù)最多相差一個。

任給一個測試信號x(t)，IMF的提取過程如表1所示。

表1 EMD算法Tab.1 EMD algorithm

若篩選過程在n次迭代后停止，測試信號x(t)可以被表示為

式中，r為剩余分量，代表信號的平均趨勢。

由于EMD算法中篩選IMF的兩個條件過于苛刻，因此常用另一個有效判斷工具[13-14]標準偏差(standard deviation, SD)來替代。當SD小于某個指定閾值(本文SD=0.05)時，終止篩選。其定義為

2 基于斜率和三次樣條的端點延拓算法

為描述方便，表2給出了有關符號定義和變量說明。

表2 符號定義和變量說明Tab.2 Symbol definition and variable description

由于延拓點的“好壞”將直接決定EMD分解的端點效應程度，如何最大程度利用已有的信息合理確定延拓點位置是解決端點效應的關鍵。本文的設計思路是：從信號及其包絡變化趨勢兩個角度共同來控制延拓點位置。其中信號變化趨勢度量是利用在信號兩端相鄰局部極值計算兩個斜率值，并以斜率變化率作為延拓點所在直線的斜率，進而構造延拓點的直線方程。另一方面，采用CSBM方法確定延拓點需滿足的另一個方程。最后通過聯(lián)立求解兩個方程來確定延拓點的坐標位置。這種設計思路同時充分考慮了信號及其包絡的變化趨勢，進而一定程度也克服了CSBM僅依靠包絡線來確定延拓點位置的局限性。

該算法需在信號兩端各延拓一個局部極大值點和一個局部極小值點。下面以信號左端延拓點為例，介紹并描述算法，算法示意圖如圖1所示。右側延拓點可在此基礎上推導得到。

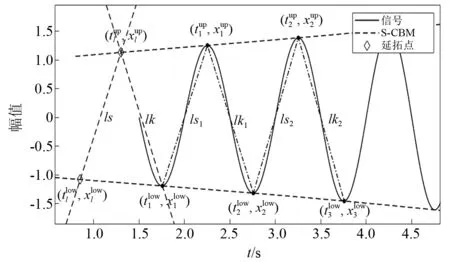
圖1 基于S-CBM的信號左端延拓Fig.1 Extension of the signal’s left end of by S-CBM

表3 綜合斜率和CSBM的端點延拓方法Tab.3 Algorithm description of end condition method combined slope and CSBM

表3(續(xù))

圖1示例了按照表3算法流程得到阻尼正弦信號x(t)=sin(2πt)·e0.1t左端延拓極值點的計算情況(此時第一個極值點是極小值點)。

3 試驗結果與性能分析

本文設計了四個模擬信號和兩個實際工程應用信號對算法性能進行測試。四個模擬信號簡述如下：第一個測試信號采樣頻率為200 Hz；第二個是由兩個調幅信號組成的采樣頻率為300 Hz的信號；第三個由高、中、低頻信號構成，采樣頻率為400 Hz；第四個例子為一個非平穩(wěn)信號，采樣頻率為200 Hz。四個信號的數(shù)學表達式定義如下，信號波形如圖2所示。兩個實際工程應用信號來自美國凱斯西儲大學軸承數(shù)據(jù)中心的一段正常電機驅動端加速度以及風扇端加速度的數(shù)據(jù)[16]，分別記為x5(t)和x6(t)，如圖3所示。

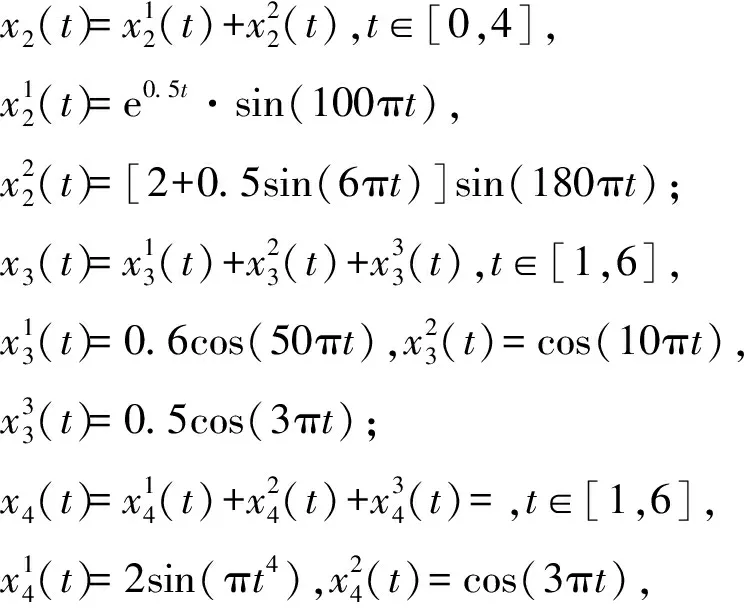
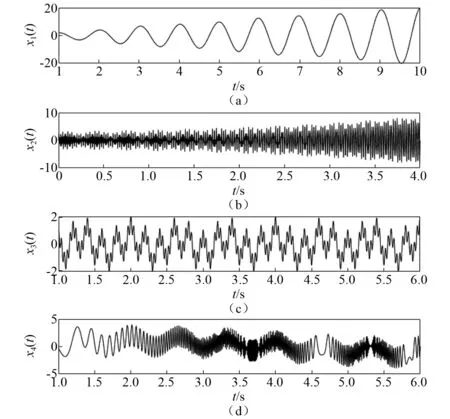
圖2 模擬信號Fig.2 Analog signals

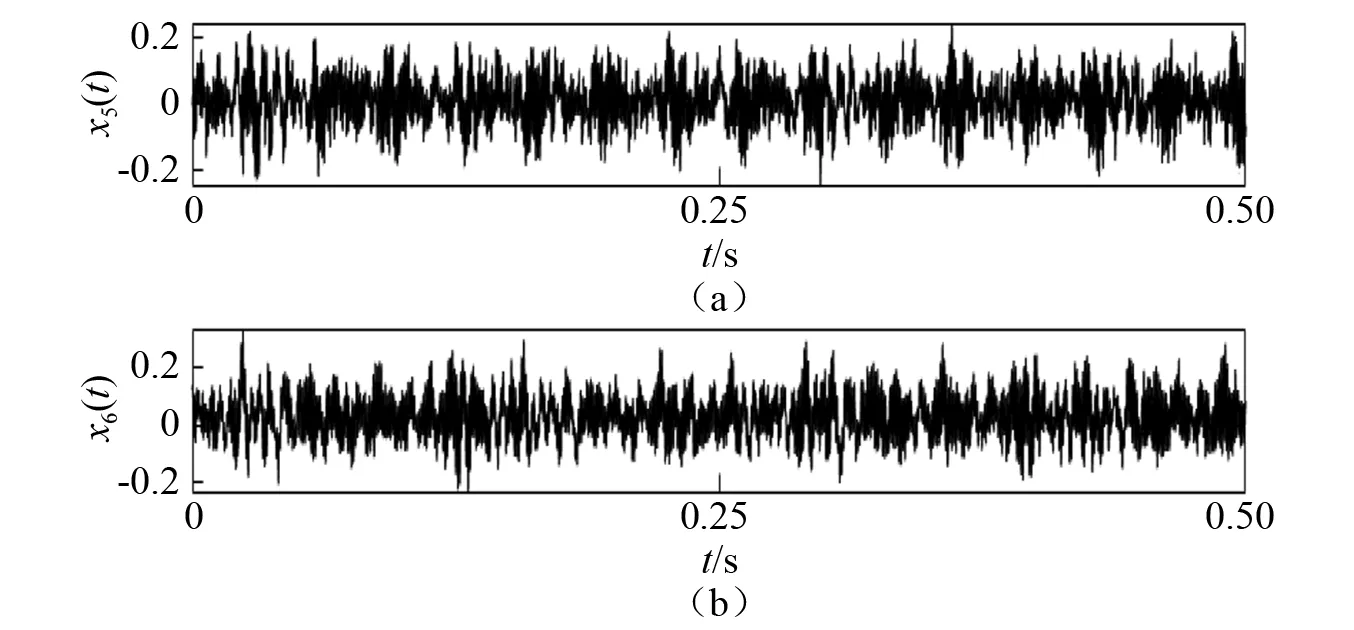
圖3 實際工程信號Fig.3 Practical engineering signals

3.1 算法性能度量指標

本文考慮三個度量指標對延拓效果進行評估。

第一個度量指標是由Huang等提出的正交指數(shù)(index of orthogonality, IO)，其定義為

式中：x(t)為原始信號；IMFi(t),IMFj(t)分別為原始信號x(t)的第i、第j個IMF分量，IO評估IMFs的正交性。理論上，IO越小，信號分解的效果越好。

第二個度量指標是均方誤差(mean squared error, MSE)，該指標對具有確定分量的輸入信號進行評估，MSE定義為

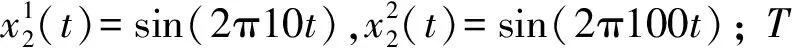
第三個指標定義為能量誤差θ。在EMD分解過程中，所有IMF的能量總和應等于原信號的能量，但由于能量泄漏等原因，IMF的能量總和往往無法與原信號保持一致。因此可以通過比較EMD分解前后的能量，評估端點效應的影響程度。能量誤差θ可描述為

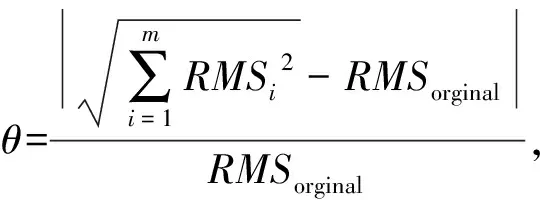
式中：si(t)為原始信號或IMF分量；RMS為信號的有效值；m,n分別為IMF的總個數(shù)和樣本數(shù)；θ值越小，信號分解效果越好。

3.2 試驗結果對比

本節(jié)僅以信號x1(t)為例，對比ISBM，CSBM和S-CBM三種不同延拓方法得到的極值點和包絡線，如圖4所示。

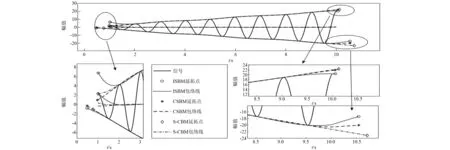
圖4 基于三種不同方法的信號x1(t)的延拓點、上下包絡線和平均包絡線Fig.4 Extended points, upper envelops, lower envelopes and mean envelopes of signal x1(t) based on three different methods

從圖4中可以看出，在該時間序列中，基于ISBM延拓的左端極大值點和右端極小值點沒有很好地反映信號變化趨勢。這是因為在求解延拓點所在直線的斜率時，ISBM沒有考慮斜率變化過大帶來的影響，導致延拓點出現(xiàn)較大誤差。CSBM在該信號中延拓效果較好，但從信號左端放大的圖像可以發(fā)現(xiàn)，CSBM延拓的局部極大值點位于信號第一個點(t1,x1)的下方，這雖然較好地反映了信號左端變化趨勢，但卻導致拓展的上包絡線在局部區(qū)域位于信號下方，也就是不能很好地規(guī)避包絡線過沖和欠沖[17]。而S-CBM由于綜合了ISBM和CSBM兩種方法的優(yōu)勢，延拓點則更好地反映了信號的變化趨勢。

3.3 性能對比及分析

本節(jié)展示了六組測試信號在三種端點延拓方法下的EMD分解效果以及評價指標結果。為了更好地分析三種方法的性能，將三種端點延拓方法提取的IMF展現(xiàn)在同一張圖中，其中最后一個IMF分量為剩余分量，代表信號的平均趨勢。需要注意的是，由于EMD延拓算法的不同，其篩選得到的IMF數(shù)量可能不一樣。表4、表5和表6分別示例了三種方法的正交指數(shù)、均方誤差和能量誤差對比情況。

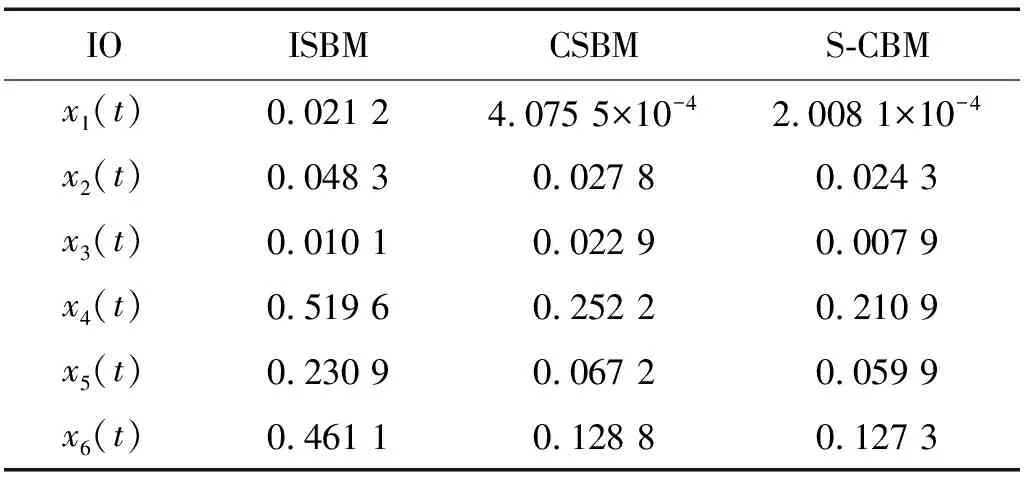
表4 三種不同延拓方法的IO結果對比Tab.4 IO results of the four signals by using EMD for three methods

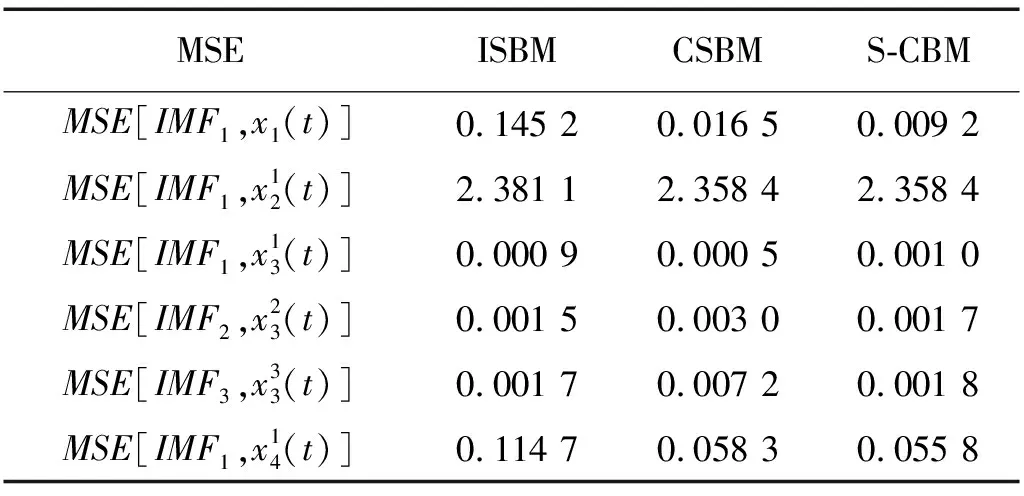
表5 三種不同延拓方法下的MSE結果對比Tab.5 MSE results of the four signals by using EMD for three methods

表6 三種不同延拓方法下的θ結果對比Tab.6 θ results of the four signals by using EMD for three methods

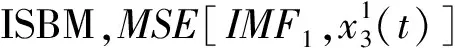
從定性的角度，對比圖5～圖10中三種延拓算法的EMD分解結果，發(fā)現(xiàn)：各信號所提取的IMF分量在兩端端點處的波動幅度越大，則端點效應越明顯，對應的端點延拓算法性能就越不足。下面以信號x1(t)為例，結合該信號的分解結果(見圖5)來展開說明。對比圖5中的IMF1，發(fā)現(xiàn)ISBM提取的IMF1在左側端點處波動幅度明顯大于CSBM和S-CBM所提取的結果，這一現(xiàn)象在后續(xù)的IMF2，IMF3及IMF4中表現(xiàn)更為突出。也就是說，對于x1(t)，ISBM所提取的各IMF分量在兩端的波動幅度明顯大于CSBM和S-CBM所提取結果的波動幅度。相對而言，CSBM和S-CBM兩種方法提取的IMF波動幅度較小。但由于S-CBM集成了ISBM和CSBM的優(yōu)點，相比較而言，S-CBM的波動幅度要小于CSBM。其他信號提取結果可以類似分析。顯然，所提取的IMF波動幅度越大，則端點效應越明顯，所以，定性分析的結果與前面定量分析的結果是一致和吻合的。

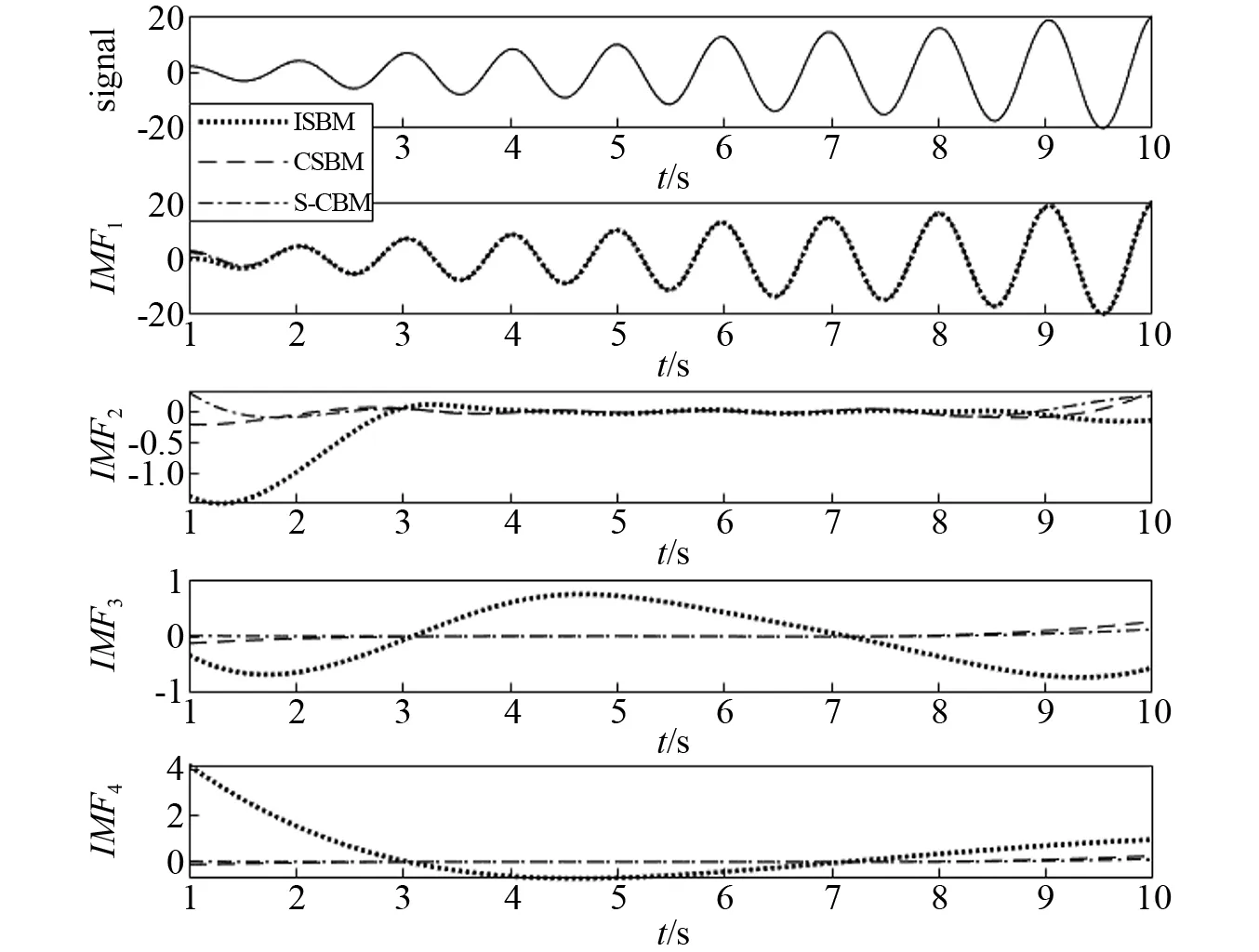
圖5 基于三種方法的x1(t) EMD分解結果Fig.5 EMD results of x1(t) based on the three methods

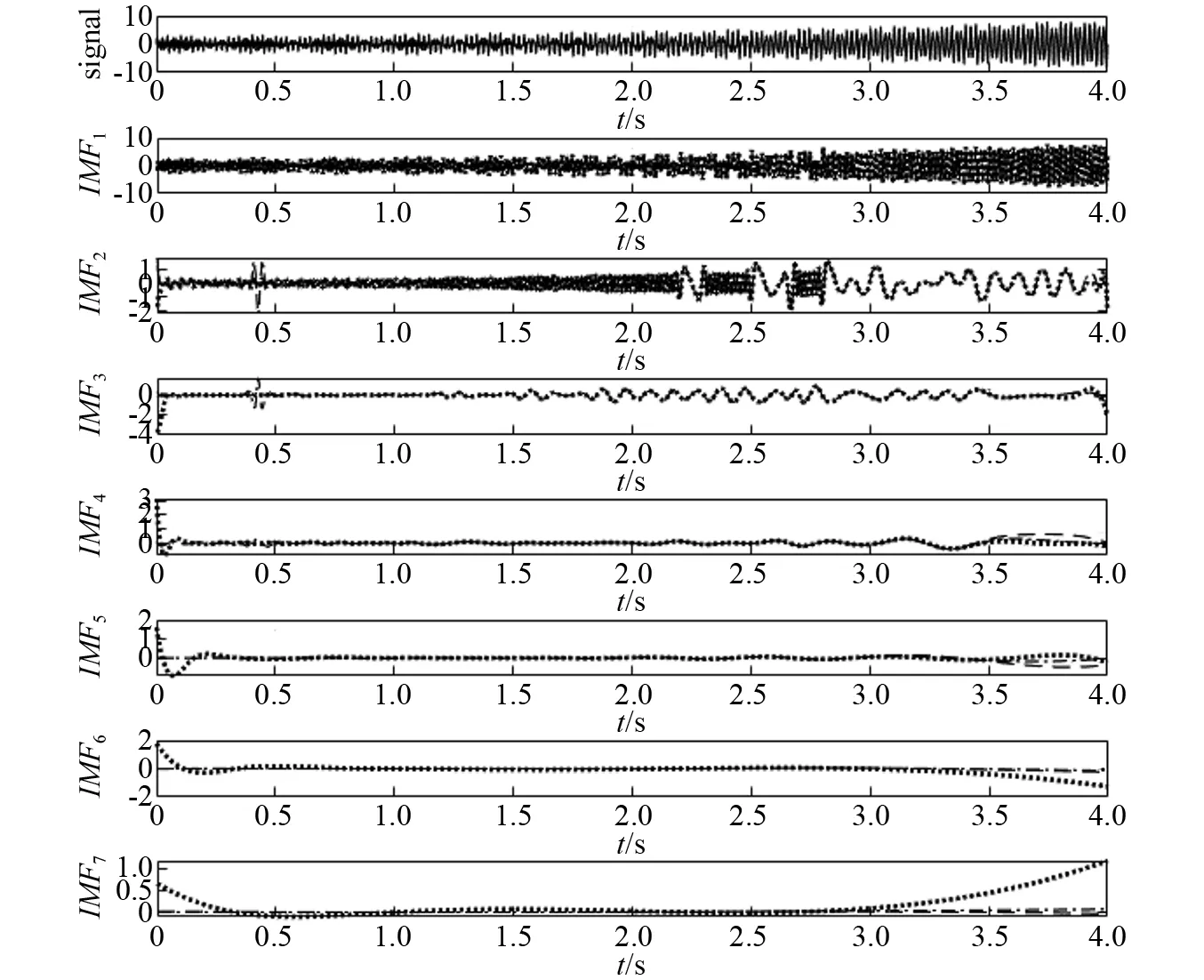
圖6 基于三種方法的x2(t) EMD分解結果Fig.6 EMD results of x2(t) based on the three methods

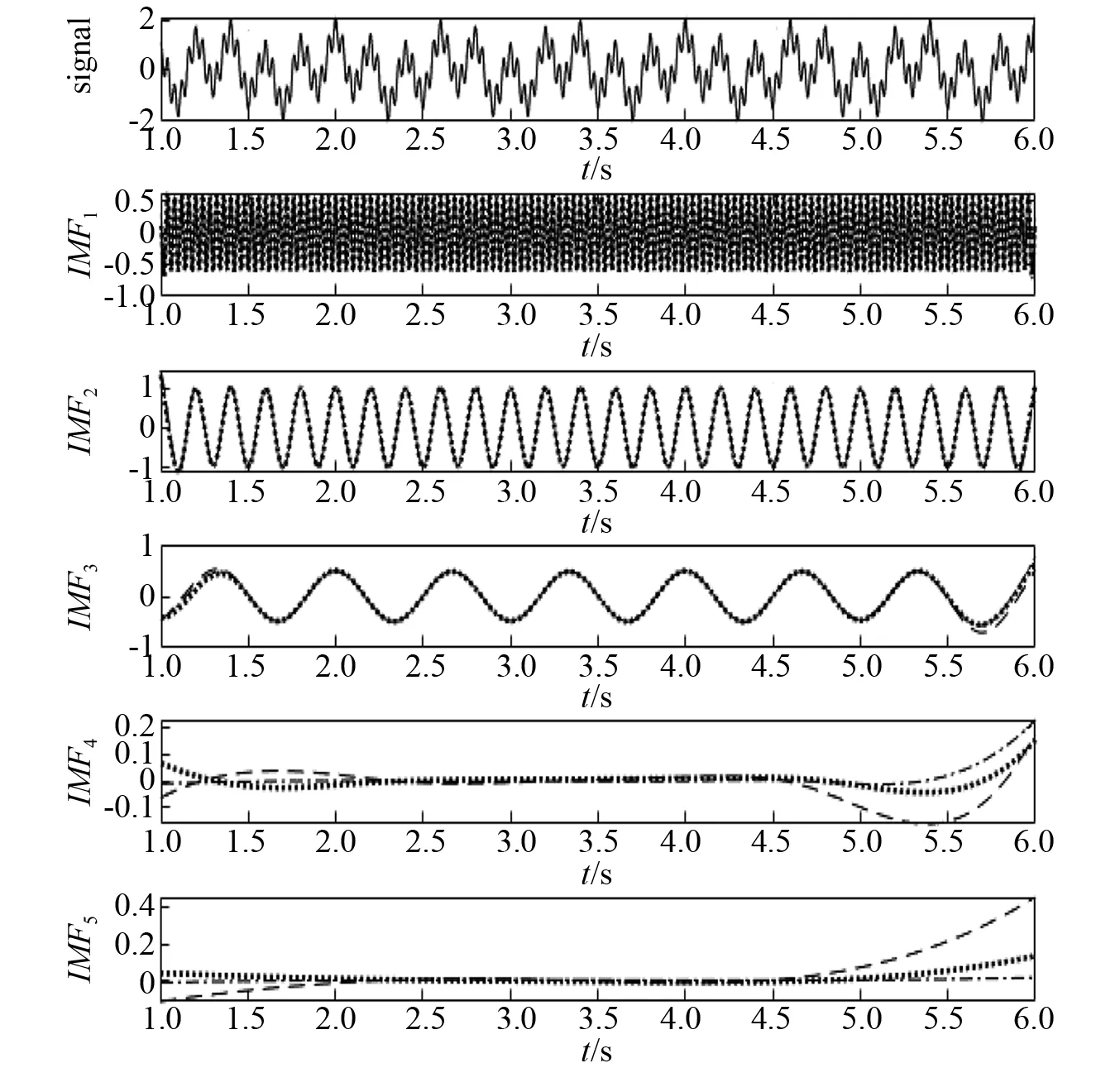
圖7 基于三種方法的x3(t) EMD分解結果Fig.7 EMD results of x3(t) based on the three methods

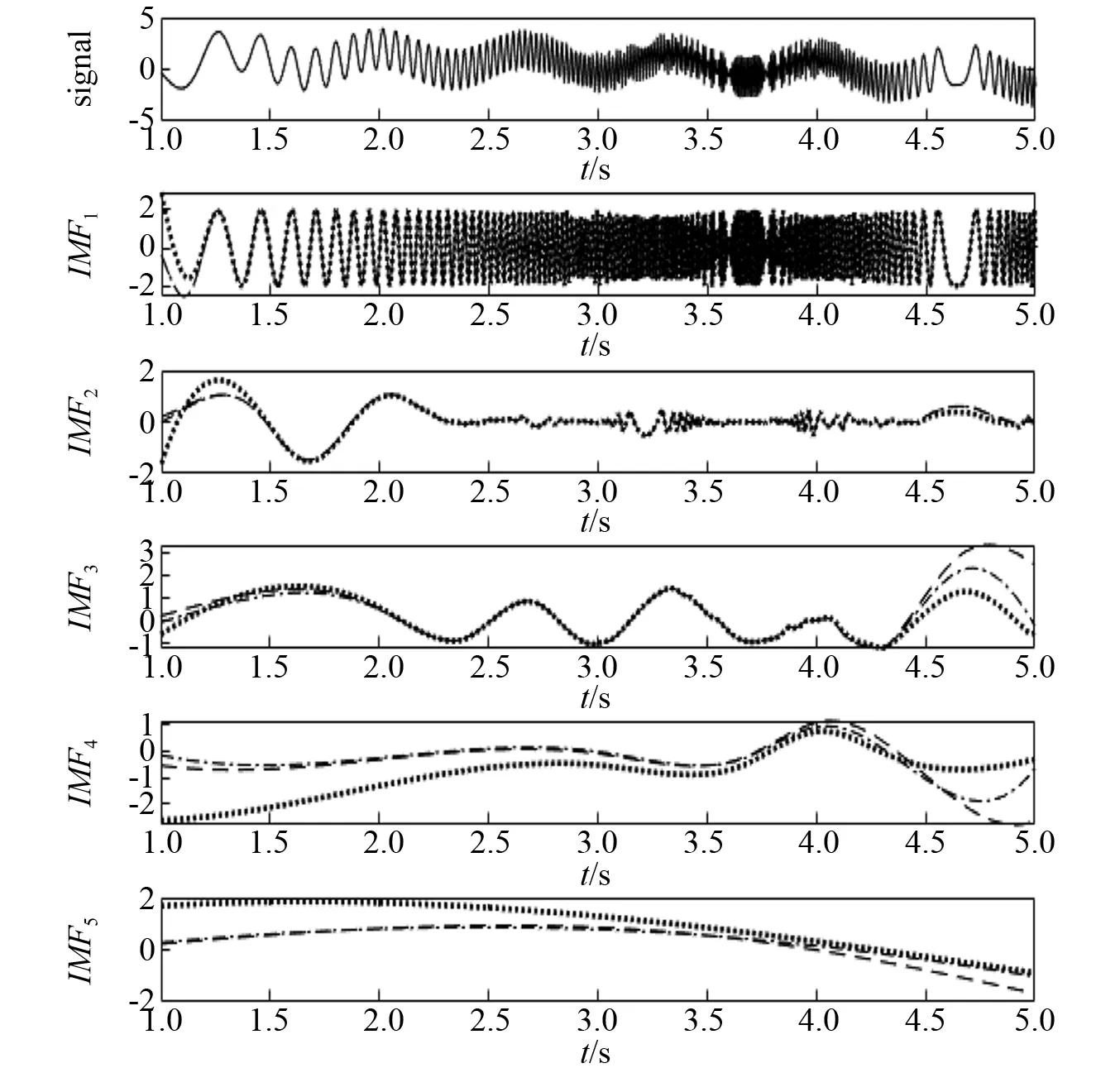
圖8 基于三種方法的x4(t) EMD分解結果Fig.8 EMD results of x4(t) based on the three methods

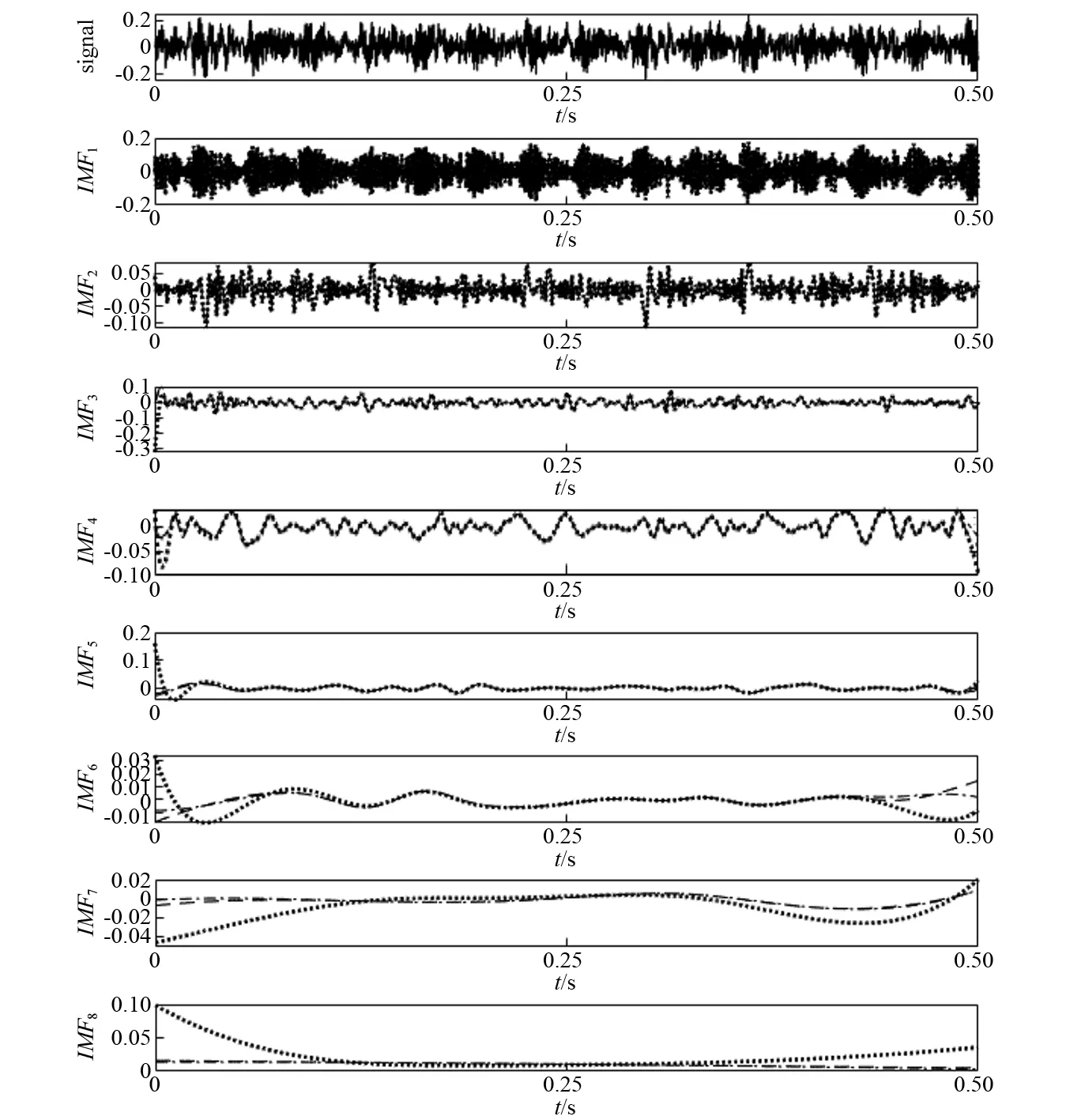
圖9 基于三種方法的x5(t) EMD分解結果Fig.9 EMD results of x5(t) based on the three methods

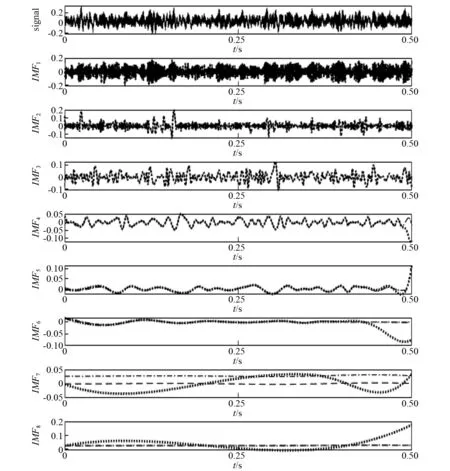
圖10 基于三種方法的x6(t) EMD分解結果Fig.10 EMD results of x6(t) based on the three methods

總體而言，試驗對比結果表明：本文所提出的方法在性能上整體優(yōu)于CSBM和ISBM。

4 結 論

本文針對CSBM延拓算法存在的缺陷，提出了基于斜率和三次樣條相結合的端點延拓方法。該方法根據(jù)信號端點的變化趨勢，并利用延拓前后包絡線在公共區(qū)域完全重合的特性唯一確定延拓點位置，克服了CSBM在設置延拓點坐標時沒有充分考慮信號趨勢的不足，進而使延拓點坐標確定更合理。模擬和實際工程應用測試信號以及IO，MSE和θ三個度量指標的試驗對比結果表明：本文提出的方法在抑制端點效應上總體性能更好。這也是我們在前期工作基礎上，對CSBM中延拓點坐標選取的一種完善和改進。需要說明的是，本文所提方法涉及的有關理論我們在Xu等的研究中已展開了詳細論述。

針對本文工作，下一步的研究主題主要包括如下兩個方面：一是EMD提取IMF的迭代收斂理論證明，進而為端點延拓算法設計提供理論指導；二是端點延拓算法設計的數(shù)學實質揭示。