基于任務的維修保障設備攜行配置研究

李黃琪，蔡開龍*，郝 明，薛紅陽，濮志剛，陳 勇

（1.南昌航空大學 飛行器工程學院，江西 南昌 330063；2.空軍工程大學 航空機務士官學校，河南 信陽 464000）

維修保障設備是飛機保障資源的重要組成部分，建立科學的飛機保障設備配備標準，合理配置維修保障設備是確保飛機保障任務順利完成的前提和基礎。基于不同的飛機作戰任務，需要攜帶的維修保障設備會有差異，如果維修保障設備配置過少，將導致保障工作出現“人等設備”的情況，直接影響飛機保障工作的進度；如果維修保障設備過多，雖然能夠保證維修工作的順利開展，但是會增加飛機的負載，進而影響飛行任務的執行效率，甚至可能出現不必要的安全隱患。所以科學合理的航空維修保障設備配置方案，可提高維修保障設備的利用率，大幅縮減航空維修保障任務的等待時間，同時還能保障飛機戰備完好率，進而緩解現階段航空維修保障能力不高的現狀。

目前分析維修保障設備的研究有：根據分析維修任務的分配和保障資源的需求，定性地確定備件需求品種[1]；運用Petri 網理論[2]構建模型，獲得所需的維修保障裝備；運用排隊論理論對維修保障裝備數量進行計算；應用多約束條件下維修保障設備配置方法。以上方法都沒有定性定量相結合的分析，一部分方法只是主觀地給出了需要攜帶的維修保障設備品種，另一部分方法是客觀的理論研究并沒結合具體的飛行任務分析。因此本文通過定性定量相結合的方法分析3 種飛行任務確定出3 種維修保障設備的類型，并根據飛機維修過程建立排隊系統。最終建立評估模型對滿足要求的方案進行評估，選出最優維修保障設備攜行方案[3-9]。

1 維修保障設備攜行配置方法的整體思路

維修保障設備攜行優化方法整體思路模型，如圖1 所示。首先本文根據飛行任務之間的差異，將飛行任務類型分為：基本飛行、任務一飛行和任務二飛行；其次確定出在不同的飛行任務下所需要攜帶的維修保障設備品種的分類，并與相關的飛行任務類型相對應。而維修保障設備品種的數量確定，可以根據飛機維修的過程建立排隊系統，通過機群數量、飛機裝備的故障率和維修設備的修復率計算出需要維修保障設備的數量。由于飛機飛行所要求的維修保障設備數量是越多越好，但是所能攜帶的空間有限。所以需要在評估優化中選用戰備完好率、等待維修時間和攜行空間3 個評估優化指標用熵權法-TOPSIS[10]法對給出的所有維修保障設備攜行方案進行評估，最后篩選出最優維修保障設備攜行方案。

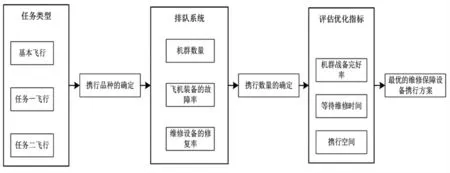
圖1 維修保障設備攜行優化方法思路模型

2 建模分析

2.1 維修保障設備攜行品種的確定

航空維修保障按照作戰、訓練任務不同，有不同的保障任務。基于任務類型的不同，我們可以把飛行任務分為：基本飛行，任務一飛行和任務二飛行。基本飛行是指只需滿足日常飛行訓練任務，其維修內容為日常維護；任務一飛行是指需要執行任務一的飛行，其維修內容有日常維護還有任務一需求的維修保障；任務二飛行是指在飛行期間飛機需要進行任務二的飛行工作，其維修內容有日常維護和任務二飛行所需要的維修保障。根據飛機要執行的任務類型可以將需要攜帶的維修保障設備分為3 個類型：（1）基本飛行包，主要是按照典型出動規模，保障飛機基本飛行必要的保障設備；（2）任務一飛行包，主要是飛機在執行任務一飛行中所需要的維修保障設備；（3）任務二飛行包，主要是按照典型出動規模，完成飛機任務二飛行所需要的保障設備。見表1。其中的關鍵維修設備定義為完成某項維修保障任務，使得任務可行而必不可少的維修設備。換句話說，缺少了該維修設備，該維修保障任務就不可能完成。不同的飛行任務，對于關鍵維修設備的要求是不同的，比如需要掛彈飛行時，武器系統檢測設備必須要充足可用，能夠在規定時間內滿足掛彈準備和檢查工作，武器系統檢測設備就是關鍵維修設備；執行日常飛行訓練任務或不掛彈飛行任務時，武器系統檢測設備就可以不必攜帶，因為缺少它不影響保障任務的完成，因此，該設備可看作該典型任務下的非關鍵維修設備。

表1 任務類型及用到的關鍵維修設備

2.2 維修保障設備攜行數量的確定

飛機維修保障的過程在維修保障設備和工具充足的情況下，無須等待直接開展維修工作，維修完成以后，維修保障設備和工具等到下一個修理任務需要時使用；在維修設備和工具不滿足需求的情況下，待修飛機進入維修隊列等待，所以整個過程可以看作多顧客多服務臺的排隊系統。在一定的時間內若飛機停機維修的數量過多，則可能出現排隊現象，導致機群的戰備完好率因維修設備數量過少而降低。因此，維修設備的數量與機群的戰備完好率直接相關。

根據排隊論理論，該問題可看作是顧客源為有限的模型（M/M/c/∞/m）。假設y 表示飛機數量，c 表示維修設備套數。因此，y 為飛機數量（即M/M/c/∞/m 模型中的m），c 為維修設備套數（即M/M/c/∞/m 模型中的c）。M/M/c/∞/m 系統指飛機按照泊松流進入維修，維修時間間隔符合負指數分布，有c 個維修設備的并列維修系統。在該系統中，需要維修的飛機到達維修點后排成相應的隊列，接受與維修專業特點相適應的維修設備的修理，每個維修設備的維修時間完全服從μ 的負指數分布，維修完畢后飛機按要求離開。該系統中，飛機的總量為y，并且存在y＞c，飛機裝備的故障率是常數λ，每個維修設備存在總體相同的修復率μ，同時，各維修設備的任務是獨立的。

本文假設所有類型的維修保障設備在進行維修工作時都滿足以下4 個條件。

（1）在某段時間間隔內，出現飛機維修任務的概率與這一時段的起始時刻無關，只與這時段的長短有關。

（2）飛機維修任務的數量與不同時間間隔無關，是相互獨立的，即滿足無后效性。

（3）假設在足夠小的時間內，不能同時出現2 個以上的飛機維修任務（這種情況現實中基本成立），即，p（t）為同時出現2 個以上飛機維修任務的概率。

（4）在任意一段時間內有產出y 項飛機維修任務的概率為1，即滿足有限性：。

如果飛機維修任務滿足以上分析的4 個條件，依據巴爾姆-欣極限定理[8]斷言：若能保證每個相互獨立的小強度流是平穩有序的，則足夠多的這些小強度流之和近似滿足Passion 輸入。因此我們可以認為，在t時間內有y 項需要進行維修的任務的概率服從強度為λ 的泊松分布

則在有y 架飛機需要執行維修任務時，該保障設備平均利用率（服務強度）為，式中λ 為飛機裝備的故障率。c 為保障設備數量，μ 為設備平均修復率，有了設備的平均利用率，就可以利用M/M/c/∞/m 模型確定執行某一任務期間的保障設備數量。

根據排隊論M/M/c/∞/m 模型理論分析，可求得狀態

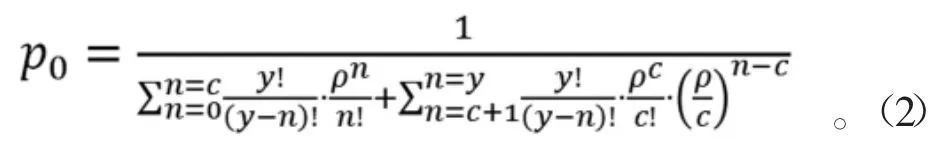
n 為受損飛機裝備數量，如果0≤n≤c，則

如果c＜n≤y，則

系統運行指標求得如下：

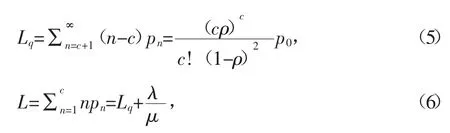
式中：Lq為等待修理的平均飛機裝備數量，L 為系統中需維修的平均飛機裝備數量（正在接受維修的飛機裝備數量與正在等待維修的飛機裝備數量之和）。

3 維修保障設備攜行方案評估分析

維修保障設備優化評估指標體系是為了維修保障設備優化評估問題用較科學的數學方法進行量化處理，必須針對評估方案和評估目標建立一個科學的評估指標體系。維修保障設備的評估優化指標主要有3個，機群戰備完好率δ、機群等待維修時間Wq和攜行空間V。機群戰備完好率是指裝備系統的戰備完好性在預定的平時與戰時的利用率下承擔和保持執行規定任務的能力，在多種維修任務并行的情況下本文將維修任務最低的戰備完好率定為機群的完好率。機群等待維修時間這一指標是為避免排隊的隊伍過長造成擁堵，不利于維修保障工作的開展，在多種維修任務并行的情況下本文將維修任務最長的等待維修時間定為機群的等待維修時間。攜行空間是指在攜行運輸中可以存放維修保障設備的空間（體積）有限的，攜行空間可以看作是約束我們攜帶維修保障設備數量的指標。通過熵權法可以確定3 個評估優化參數的權重，再用TOPSIS 法對所有滿足條件的維修保障設備攜行方案進行排序，選出最優的維修保障設備攜行方案。

熵權法-TOPSIS 法評估模型：設有m 個方案，n 個指標，Xij為第i 個樣本第j 項指標的數值。因為方案指標的要求不同，可用極值標準化方法將指標分為極小值型指標與極大值型指標。其中，極小值指標是指標數據越小理想要求越好的指標：

極大值指標是指標數據越大理想要求越好的指標：

歸一法，為了消除標準化后的指標值對數計算的影響，使得所有方案的指標都落在[0，1]之間，計算公式為：

計算第i 個方案第j 項指標占所有樣本第j 項指標之和的比重Pij，公式為：

計算所有指標的熵值Ej，公式為：

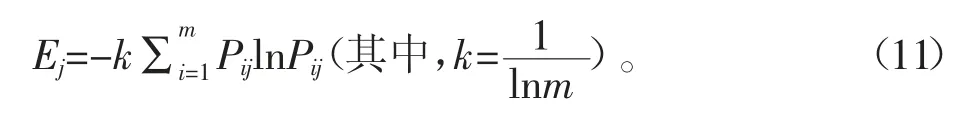
計算所有指標的權重Wj，公式為：

對所有方案數據進行加權處理，公式為：

計算的所有方案數據的最好解Y+和最差解Y-，公式為：

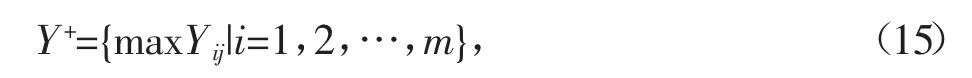
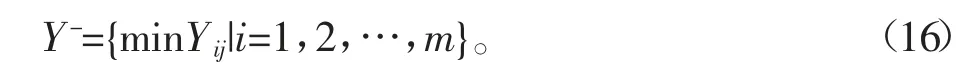
分別計算方案數據與最好解和最差解的距離Di+和Di-，公式為：

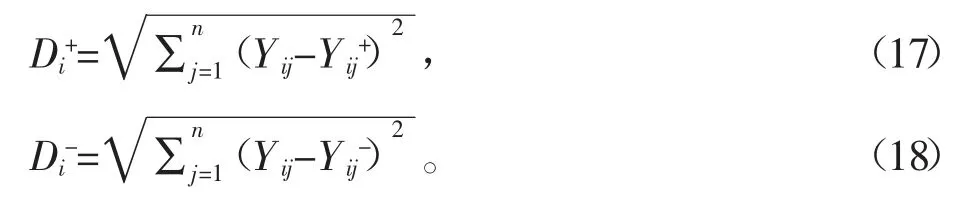
計算方案數據與最優解的接近程度Ci，所有綜合得分公式為：

4 案例分析

假設典型任務下，需要出動某飛機機群，共有12架飛機。執行該任務需要用維修保障設備A、B、C 和D 4 種，維修保障設備A、B、C 和D 的信息，見表2。在攜行空間1 200 cm3內，要保證每架飛機等待維修時間不能超過3 h，并且飛機機群戰備完好率85%以上，最優應該攜帶多少設備？

表2 維修保障設備信息

通過分析我們可以知道A、B、C 和D 設備單個占用空間分別為：140 cm3、170 cm3、116 cm3和77 cm3；用排隊論計算后，維修保障設備數量指標表見表3，從表中可以得出A、B、C 和D 4 個維修保障設備至少要攜帶2 個以上才能滿足任務需求。

表3 維修保障設備數量指標表

因為機群的戰備完好率是取所有設備完好率最低的，機群的維修等待時間也是取所有設備維修等待時間最長的。隨著有某些設備維修保障數量的增加，機群的維修等待時間和戰備完好率并沒有發生改變。從表4 中的七個方案我們可以得出，方案一到方案四隨著維修保障設備的增加并沒有降低機群等待維修時間，也沒有提高機群戰備完好率，所以方案一到方案四中我們優先維修設備數量少的方案一，再由熵權法-TOPSIS法對方案一、方案五、方案六和方案七進行打分排序。

表4 方案評估參數表

通過熵權法求得戰備完好率、等待維修時間、攜行空間3 個評估指標的權重分別為：w1=0.2765，w2=0.2957，w3=0.4278;再將w1，w2，w3帶入TOPSIS 法中得出所有方案的得分：方案一為0.4893、方案五為0.2037、方案六為0.2140、方案七為0.0929；由此可以看出方案一>方案六>方案五>方案七，所以我們的最優方案是方案一，需要攜帶維修保障設備A、B、C 和D 各2 個。

5 結論

本文采用定性定量相結合的方法進行系統的分析，首先對飛行任務進行分析，確定出3 種維修保障設備的分類，進而可以根據飛行任務確定出需要攜帶的維修保障設備的品種；其次運用了排隊論方法和熵權法-TOPSIS 法，對攜帶不同的維修保障設備數量進行分析，并給出最優的維修保障設備攜行方案。該方法的研究能夠為確定飛行部隊維修體系的研究提供參考，具備一定的應用價值，但在多軍兵種聯合作戰的大趨勢下如何確定適用于其他軍兵種力量的維修保障體系仍是有待攻克的難題，因此未來在其他軍兵種力量的維修保障體系需要進一步研究。