汽車鋰離子電池溫度優化控制及數值模擬

張鳴鑫，薛長峰，邱海龍

1.鹽城工學院 電氣工程學院，江蘇鹽城224002；2.鹽城工學院 數理學院，江蘇鹽城224002

近年來，環境污染和能源危機問題不斷加劇，空氣污染已經對人類健康產生了影響。電動汽車因具有減少環境污染、改善空氣質量的優勢逐漸占據汽車市場［1］。電動汽車所用的鋰離子電池具有低污染、低能耗的優點，但其性能對于溫度變化十分敏感，電池組中各電池單體之間溫度過高或溫度分布不均勻都會對電池產生不可逆轉的影響［2］。鋰離子電池工作的最佳溫度區間為20~40 ℃，并且電池組中各電池單體間的最大溫差一般應控制在5 ℃以內［3］。若在電池充放電過程中使用不當，電池內部極有可能因溫升過高發生熱失控，導致電池發生起火、冒煙或爆炸等危險，從而引發事故甚至威脅人身安全［4］。因此，高效的電池溫度控制設計對電動汽車的使用壽命和安全性能十分重要。

目前，電動汽車鋰電池的散熱方式主要有空氣冷卻、液體冷卻和相變材料冷卻3 種。空氣冷卻又被稱為風冷，是一種相對比較簡單、設計成本低的技術，基于空氣的流動與電池產生對流換熱［5］，但其散熱能力有限，處理溫度較高或高放電倍率情況下的電池組時，很難達到較為理想的散熱效果，無法保證電池組的溫度均勻性［6］。相變材料（Phase Change Material，PCM）冷卻是通過改變材料狀態的方式吸收或釋放大量熱量，散熱效果與風冷相比較為明顯，但其本身的儲能元件沒有辦法傳遞熱量，往往需要與其他方式聯合進行散熱［7］。液體冷卻是最為常見的一種散熱方式，主要是將冷卻液注入冷卻板或冷卻管道中，通過低溫液體循環流動實現對電池組的快速散熱［8］，因其控制方法較為成熟、冷卻效果明顯而被廣泛使用。

很多學者對液體冷卻的結構優化進行研究，通過冷卻液的溫度及流速、流道的類型及數量等參數的變化進行設計。Su等［9］通過建立基于遺傳算法的優化模型，分別對冷卻板厚度、冷卻液流入溫度和流速進行了分析，并且建立了基于第二代非支配排序遺傳算法（NSGA-II）的多目標優化模型，提升了電池組的散熱效果。馮能蓮等［10］設計出了新型蜂巢式液冷電池組，分別對不同冷卻液流量、溫度進行分析，電池組溫度均勻性較穩定，最高溫度變化顯著，驗證了其方案下模型的準確性。但是，不同因素對電池組的影響，以及電池組的結構設計等還需要進一步深入研究，以提高電池組的散熱效果。本文針對電池組最高溫度和各電池單體溫度不均勻的問題進行研究，分析冷卻液流道數、電池嵌入冷卻板距離d和冷卻液流速3 種因素對電池組溫度的影響，并通過正交試驗尋求冷卻電池組的最佳組合方案。

1 電池組冷卻模型

1.1 電池組模型的建立

本文對電池組最高溫度和電池單體間的溫度均勻性進行優化控制。對電池組模型進行簡化設計，其中電池單體型號為18650鋰電池，建立5 行10 列對齊排列的圓柱形單體電池組模型，電池組模型的尺寸為216 mm×116 mm×65 mm；各個電池單體行間距為22 mm，列間距為22 mm；冷卻液流道寬度為3 mm，長度為216 mm；電池組嵌入冷卻板的距離d為1 mm；冷卻板的厚度為1 mm。電池組模型結構如圖1所示。

冷卻板模型如圖2所示，電池單體參數如表1所示。電池組模型冷卻過程中，冷卻液從進口端流入，經過冷卻板與電池組進行熱交換，再從出口端流出，達到降低電池組溫度的目的。

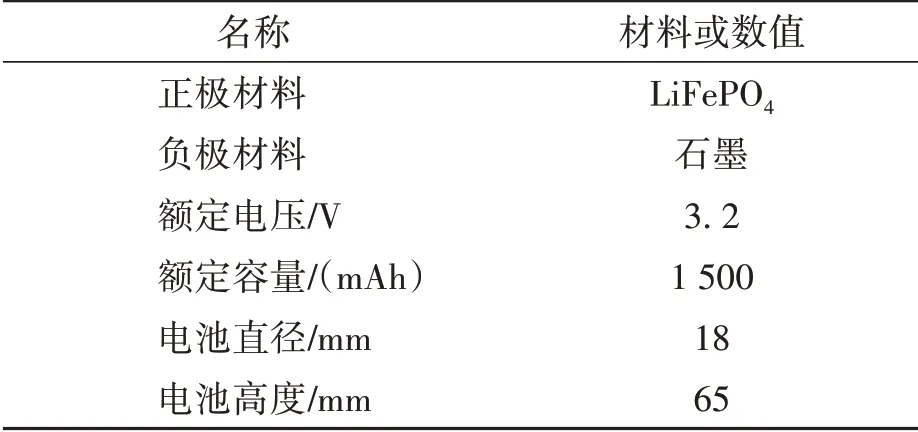
表1 電池單體參數表Table 1 Battery unit parameters table

1.2 材料屬性

本文中電池組模型選用體積濃度50%的水乙二醇溶液作為冷卻液的冷卻介質，選用鋁板作為冷卻板，各種材料的熱物性參數如表2所示。

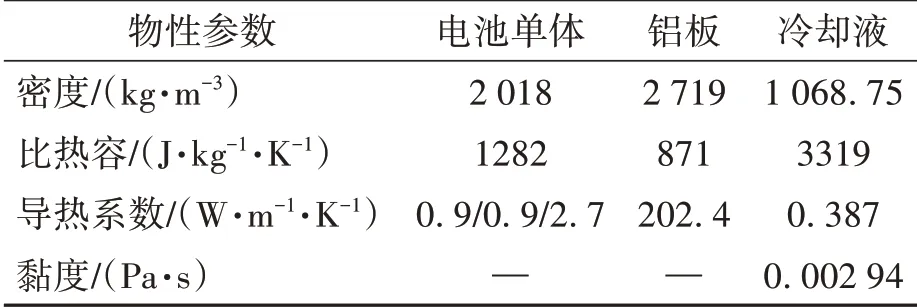
表2 各種材料的熱物性參數Table 2 Thermal physical parameters of various materials

2 電池組生熱原理及參數

2.1 條件假設

充放電過程中，鋰電池內部反應機理十分復雜，研究表明電池組生熱來源主要包括熵變產生的反應熱、副反應熱，與材料內阻有關的焦耳熱，以及極化阻抗產生的極化熱等4個部分［11］。為分析電池的生熱狀況，先對電池組模型提出如下假設：

（1）各電池單體的材料，以及密度、比熱容等物理參數相同；

（2）電池各個方向的發熱量恒定且均勻；

（3）電池單體各向導熱系數恒定；

（4）電池內部的熱輻射不考慮。

2.2 控制方程

由傅里葉定律和能量守恒定律，可得到電池導熱微分方程為：

式中：ρ為電池的密度，kg/m3；cp為電池的比熱容，J/（kg·K）；λx、λy、λz分別為電池在3 個方向上的導熱系數，W/（m·K）；T為電池的溫度，K；q為電池單位體積的生熱速率，W/m3。

因電池實際生熱速率很難測量，D.Bernardi等提出了電池生熱速率數學模型，認為電池內部溫度是均勻分布的，溫度隨時間變化，電池熱量來源主要包括反應熱和焦耳熱兩部分［12］。

式中：I為電池的電流，A；Eoc為電池的開路電壓，V；E為電池的實際工作電壓，V；dEoc/dT為溫熵系數；V是電池的體積，m3。

在電池溫度控制中，鋰電池產生熱量通過熱傳導方式傳遞，與空氣形成熱對流。因此，冷卻液在換熱時遵守連續性方程、能量守恒方程和動量守恒方程，如公式（3）~公式（5）所示：

式中：ρ1為冷卻液的密度，kg/m3；t為電池組放電過程中的時間，s；v為冷卻液的流速，m/s；P為冷卻液的靜壓，Pa；c1為冷卻液的比熱容，J/（kg·K）；k1為冷卻液的傳熱系數，W/（m2·K）。

模擬過程中冷卻液流動狀態要根據雷諾數Re確定：

式中：L為冷卻液的特征長度，m；μ為冷卻液的黏度系數，Pa·s。

2.3 初始條件和邊界條件

將電池組模型進行仿真時，采取速度入口和靜壓出口，靜壓力為零，設環境為1 個標準大氣壓，為驗證模型的冷卻效果，取環境溫度35 ℃，冷卻液入口溫度25 ℃，冷卻液流速0.01 m/s，電池模型外表面與外部環境產生換熱，對流換熱系數為5 W/（m2·K）。計算所得雷諾數小于2 300，故冷卻液流動選用層流模型。

在初始時刻，設電池模型溫度為環境溫度：

式中：t為時間，s；T0為環境溫度，K。

電池模型外表面溫度與環境的邊界條件為：

式中：Qc為單位面積的對流換熱量，W/m2；h為對流換熱系數，W/（m2·K）；Tw為電池模型的表面溫度，K。

放電速率是指鋰電池在規定時間內放電額定容量所需的電流值，等于數據值中電池額定容量的倍數，通常用字母C 表示。不同放電倍率下的電池單體生熱量如表3 所示，本文取放電倍率3C作為模擬數據。

表3 不同放電倍率下的電池體積生熱量Table 3 Volume heat generation of battery at different discharge rate

3 數值模擬

3.1 網格劃分

由于電池內部組成較為復雜，為了提高計算準確度，對溫度場影響較小的因素可忽略不計。電池組模型采用非結構化網格，并設置接觸面的邊界層，傳熱面進行局部網格加密處理，網格數約1 200 000 個，網格質量滿足計算精度，如圖3所示。

3.2 計算求解

電池組模型與外界空氣處于自然對流狀態，流體與固體直接接觸，故考慮無滑移邊界條件。這里采用SIMPLE 算法求解動量方程中的速度和壓力，對于非線性項采用二階迎風格式，電池組在3C 放電倍率下的放電時間設置為1 200 個步長，步長為1 s，每個時間步長迭代10次。

根據上述條件及計算方法對電池組模型進行仿真，圖4為求解過程中電池組的最高溫度、最低溫度和溫差的變化曲線；圖5 為電池組模型的溫度分布云圖。

由圖4 可知，冷卻過程中電池組最高溫度均沒有達到40 ℃，處于電池組的最佳溫度區間，但在1 200 s 的放電過程中，溫差變化曲線的最大溫差達到8.33 ℃，從第19 s 至460 s 溫差都超過5 ℃，占總放電時間的36.75%。由此可見，該方案得到的結果并不理想，因此需要對電池組進行進一步優化。

由圖5 可知，冷卻液經過鋁板與電池組進行換熱，電池組在1 200 s 終止時最高溫度為29.918 ℃，最終溫差穩定在3.947 ℃，且最高溫度均位于電池組左端。由于電池組的冷卻液入口位于右端，故右端的電池相對于左端電池溫度較低，冷卻效果明顯。

4 正交試驗分析

4.1 正交試驗設計

從電池組溫度分布情況中可以看出，電池在靠近冷卻液入口端的溫度優于出口端溫度，導致電池的較高溫度均存在于出口端。為了進一步提高整個電池組中電池單體之間的溫度均勻性，綜合考慮各影響因素，本文選擇冷卻板的流道數、電池嵌入鋁板的距離d和冷卻液流速3 個因素進行正交試驗分析。

針對每個因素選取3 個水平進行分析，正交試驗的因素和水平如表4 所示。流道數（因素A）分別選用1 流道、2 流道、4 流道，其中2 流道、4 流道的冷卻板流道示意圖如圖6 所示；電池嵌入距離d（因素B）分別取1、2、3 mm；冷卻液流速（因素C）分別取0.01、0.05、0.1 m/s。

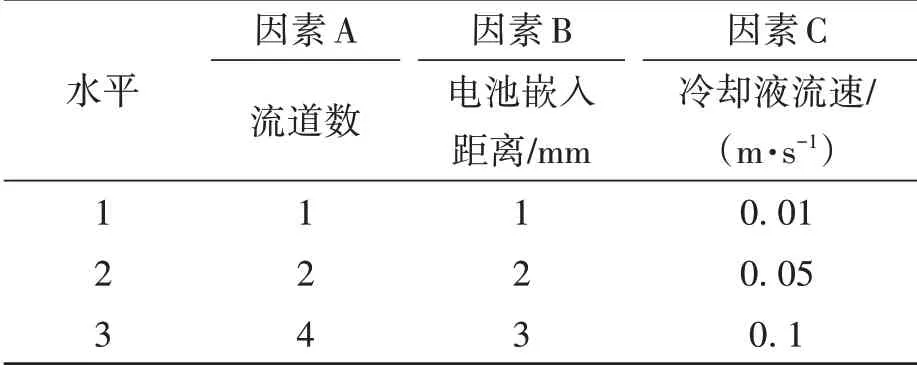
表4 正交試驗因素水平表Table 4 Orthogonal test factor level table

由于這3 個因素之間的交互作用不明顯，可以認為不存在交互作用，選擇L9（34）方案設計正交試驗表，試驗的指標為電池組最高溫度和溫差，對于不同試驗參數的組合，利用FLUENT軟件進行模擬，模擬仿真時其余所有參數均相同，正交試驗方案及計算結果如表5 所示，電池組的溫度分布如圖7所示。

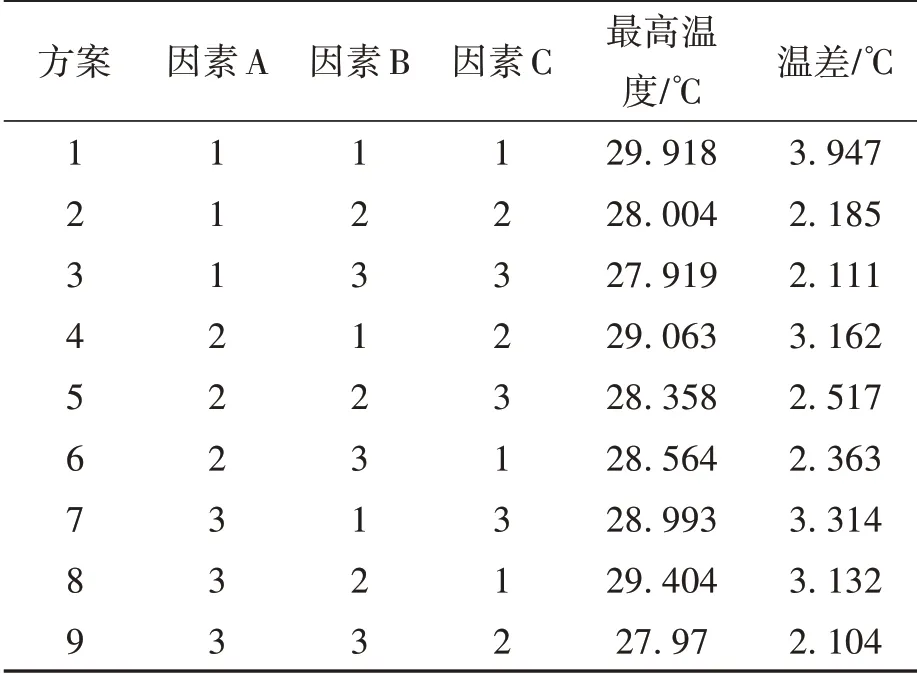
表5 L9（34）正交試驗方案及仿真結果Table 5 L9（34）Orthogonal test scheme and simulation results

4.2 正交試驗分析

本文用極差分析的方法，分析了各因素對試驗結果的影響，結果如表6 所示。極差數小代表此因素對試驗影響較小，相反，數值較大代表因素對試驗影響較大。由正交試驗數據可以看出，所有組合中電池組的最高溫度均處于鋰電池的適宜溫度范圍之內，證明該模型具有較好的控溫 效果。下面將以溫差作為試驗的研究指標，對其進行優化。

表6 電池組溫差極差分析表Table 6 Analysis of the polar variance of the temperature difference of the battery pack

由表6 可以看出，極差R大小依次為R（B）＞R（C）＞R（A），因此各影響因素的重要性由高到低分別是電池嵌入距離d、冷卻液流速和流道數。故可以認為電池嵌入距離d是電池組溫差的主要影響因素，嵌入距離d越大，鋁板與電池組的換熱面積越大，則電池組之間的溫差就小。

為進一步驗證各因素對電池組溫度的影響大小，應用SPSS 軟件對其進行方差分析，其結果如表7所示。

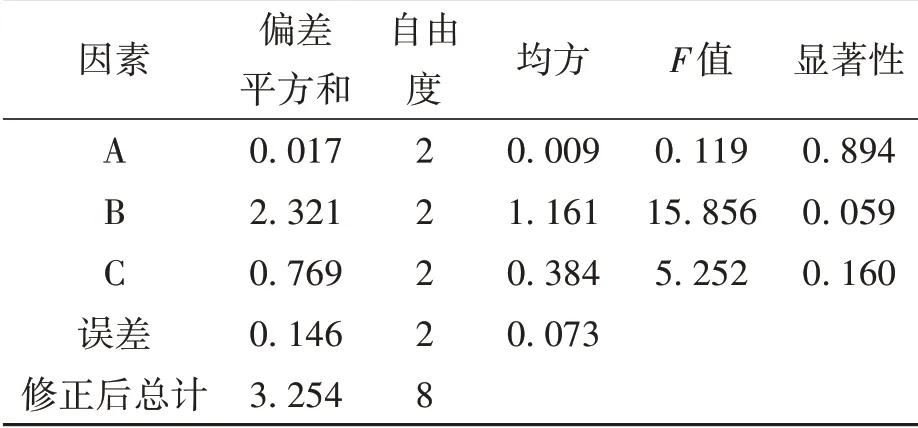
表7 電池組溫差方差分析表Table 7 Analysis of variance table for battery pack temperature difference

顯著性系數越小表示各因素對試驗指標影響越明顯。由表7 可知，電池嵌入距離d對電池組溫差的影響顯著，其次是冷卻液流速，而流道數對電池組溫差的影響不明顯。綜上，方差分析與極差分析結果一致，驗證了優化的有效性。

效應曲線可用來分析因素水平對試驗指標的影響趨勢，根據指標效應的結果選出各因素水平的最佳組合方案，其中橫坐標為各因素的各水平，縱坐標為試驗指標的平均值。圖8 為正交試驗指標效應曲線。由圖8 可以看出，隨著電池嵌入距離d的增加，電池組的溫差變化明顯，其試驗指標呈單調遞減的趨勢；2 流道電池組溫度分布相比于1 流道和4 流道的溫度分布更加均勻；冷卻液流速為0.05 m/s 時電池組的溫差小于0.01 m/s 和0.1 m/s 時的溫差。結合以上分析，可以得出對于電池組溫度均勻性最好的因素水平組合為A2B3C2，即流道數為2，d為3 mm，冷卻液流速為0.05 m/s。

利用FLUENT 軟件模擬試驗的最佳組合，如圖9 所示。由圖9 可以看出，電池組最高溫度均分布在電池組中心位置，且各電池單體之間溫差分布均勻。圖10 為電池組溫度變化曲線。由圖10 可以看出，與優化前的溫度變化曲線相比，優化后的方案冷卻效果改善明顯。在1 200 s 的放電過程中，僅在45 s 至107 s 時溫差超過5 ℃，占總放電時間的5.16%，放電終止時電池組最高溫度為27.954 ℃，溫差為2.073 ℃，與優化前相比，電池組的散熱效果提升顯著。

5 結論

本文對電池組散熱問題進行了研究，基于正交試驗設計，分析了在不同冷卻液流道數、不同嵌入冷卻板距離d、不同冷卻液流速下的數值模擬結果，最終確定了最佳組合方案。具體結論如下：

（1）由正交試驗結果可知，影響電池組溫差最顯著的因素是電池組嵌入冷卻板距離d。增加電池組嵌入冷卻板距離d，可以有效改善電池組溫差的不均勻性。本文正交試驗設計優化的最佳組合為A2B3C2，即流道數為2，電池組嵌入冷卻板距離d為3 mm，冷卻液流速為0.05 m/s。

（2）與優化前相比，優化后放電終止時電池組的最高溫度為27.954 ℃，下降6.565%；溫差為2.073 ℃，下降47.479%；最大溫差為5.437 ℃，下降34.73%，有效降低了電池組的最高溫度，改善了各電池單體之間的溫度不均勻性。