基于互信息量估計的幾何與概率聯合整形技術

梁家熙，牛澤坤，胡衛生，義理林

(上海交通大學 區域光纖通信網與新型光通信系統國家重點實驗室，上海 200240)

0 引 言

在加性高斯白噪聲(Additive White Gaussian Noise，AWGN)信道中，使用高階的正交振幅調制(Quadrature Amplitude Modulation，QAM)在高信噪比(Signal Noise Ratio，SNR)的情況下，互信息量(Mutual Information，MI)與香農極限相差1.53 dB[1]，QAM的方形星座圖是造成容量差距的原因。星座整形是一種在QAM基礎上提高MI的方式，分為幾何整形和概率整形，其中幾何整形指調整星座點的幾何分布，概率整形指調整星座點在發送信號中出現的概率。幾何整形和概率整形通過一些傳統的方式實現，例如幾何整形可以通過一定的規則調整星座圖點與點的位置，充分利用空間，但是無法證明這種方法可以得到使系統的信道容量最大的編碼方式[2];概率整形可以通過麥克斯韋-玻爾茲曼(Maxwell- Boltzmann，MB)分布調整星座點的概率分布，在AWGN信道下，證明MB分布可以達到性能最佳，但是對于其他信道而言，MB分布無法取得最佳性能[3]。

近年來，深度學習被引入物理層通信中，通信系統可以被視為一個自動編碼器，此時發端與收端都可以由神經網絡的全連接層擔任，這就是端到端的深度學習(End-to-End Deep Learning，E2EDL)通信系統[4]。E2EDL相較于傳統的通信算法優勢在于從一個全局的角度出發考慮優化，而不是將局部最優組合到一起，得到一種非全局最優的方案[5]。通過E2EDL，可以實現星座整形，訓練得到幾何整形[4]和概率整形[6]的編碼器，性能接近或超過傳統算法的最佳性能。通過E2EDL在幾何整形星座圖的基礎上做概率整形，可以取得比單獨幾何整形和概率整形更高的增益[6]。但是，目前的方法都是在固定的幾何整形上做概率整形，沒有進行聯合優化，且這些方法無法證明當前整形結果的信息量是最優的。

本文提出了一種基于互信息量估計(Mutual Information Neural Estimation，MINE)的幾何與概率聯合整形方法。MINE可以估計兩種不同分布的MI[7]，本文提出的系統利用MINE估計當前通信系統的MI，并且訓練發端編碼器以滿足最大化MI。基于MINE的系統無需訓練解碼器，可以避免解碼器誤差對編碼器訓練帶來的損失。本文提出了幾何整形與概率整形的聯合優化方式，通過訓練迭代優化幾何整形與概率整形的編碼器，使系統接近到幾何整形與概率整形所能達到的MI的極限。本文將系統在不同SNR的AWGN信道中進行仿真，比較了幾何與概率聯合整形的系統與其他方案之間的MI。仿真結果表明，幾何與概率聯合整形系統的MI高于單獨進行幾何或概率整形的系統，在SNR為10 dB的AWGN信道中，幾何與概率聯合整形的系統MI與單獨做概率整形的系統相比，有0.027 9 bit/symbol的增益；與單獨做幾何整形的系統相比，有0.041 7 bit/symbol的增益。

1 MINE原理

根據香農信息論的內容，信道輸入和輸出之間的MI的極大值就是信道容量，可以通過最大化MI的方式找到可以逼近信道容量的編碼方式。但從歷史上看，MI往往是難以計算的[8]，精確的計算僅僅適用于離散變量(可以直接求出總和)，或是用于已知概率分布的有限問題，對于更加廣泛的應用場景，MI的精確計算通常是不可能的。

2018年，來自蒙特利爾大學的Belghazi等人提出了一個基于 Kullback-Leibler(KL)散度的對偶表示的通用參數神經網絡互信息估計器，MINE[7]。MINE是一種數據驅動估計MI下界的方式，可以估計任意兩種不同分布的MI的下界，并且可以將估計值作為損失函數，將梯度沿著神經網絡估計器進行反向傳播。

MINE的原理如下：兩個變量X和Z的MI可以通過下式表示：

式中：X和Z為兩種不同的分布；I(X;Z)為兩種分布間的MI；PXZ為X和Z的聯合分布；PX和PZ分別為X和Z的邊際分布；?為兩種分布間的張量積。另外引入KL散度的概念，KL散度又叫相對熵，是兩個不同分布之間的差異的非對稱性度量，在信息論中，KL散度是兩個不同分布的信息熵的差值，表示如下：

式中：P和Q為兩種不同的分布；DKL(P||Q)為P和Q的KL散度；EP為變量在P分布下的數學期望值。P和Q都是嚴格連續的分布。根據式(1)和(2)可以推導出，MI和KL散度的關系為

接下來，MINE的重點在于KL散度的對偶表示，這份工作由Donsker和Varadhan于1983年完成，因此KL散度的對偶表示又稱Donsker-Varadhan表示[9]，具體如下

式中：e為自然對數底；T為所有函數集合R中的一個函數，T:Ω→R表示在實數域函數中存在函數T；sup為函數的上界。式(4)的意義在于，在一個由所有實函數組成的域中，一定能找到一個函數對應關系T，按照函數對應關系將P和Q的分布轉化為標量，而這個標量使得等號右側函數的值最大，而這個最大值就是P和Q的KL散度。函數T可以由神經網絡函數來表示，假設Θ為所有神經網絡所有參數的集合，因此TΘ可以看作所有神經網絡函數的集合，而TΘ是R的一個子集，因此神經網絡估計的MI與真實的MI間有如下關系：

式中，IΘ(X,Z)為通過神經網絡計算的MI的估計值，對于參數為θ∈Θ的神經網絡，根據式(3)、(4)和(5)可以推導得到：

通過式(6)，在兩個隨機分布里隨機選取聯合樣本和邊界樣本，再通過訓練找到使得樣本的MI估計值最大的神經網絡參數，這個MINE值就是兩個分布MI的下界。

因此，計算兩個不同分布的MI，可以轉變為求一個神經網絡在特定損失函數下的最大值。定義一個神經網絡，用于將兩種不同分布的變量轉化為一個標量，即Tθ(X,Z)，通過將Tθ代入式(6)可以計算得到在當前神經網絡參數θ下的MI估計值，然后將式(6)等號右邊的相反數設置為損失函數，試圖通過最小化損失函數，即最大化MI的估計值，即可取得MI的下界。

在本文中，系統使用MINE作為估計系統MI的方法，取得信道兩段的符號，通過訓練的方式找到使得估計值最大的參數θ，再通過式(6)計算得到通信系統MI的估計值。

2 基于MINE的幾何與概率聯合整形系統設計

2.1 幾何整形系統

幾何整形是通過設計星座點的位置，使得星座點之間的歐氏距離增大，從而降低解碼端分辨星座點的難度，降低誤碼率。從信息論角度考慮，幾何整形的目的是尋找一種使得信道容量最大的調制方法，獲得更高的通信速率。在基于MINE的幾何整形系統中，訓練MINE神經網絡計算信道兩端符號的MI，然后通過最大化MI的方式訓練編碼器，從而得到使得信道容量最大的調制方式。

基于MINE的幾何整形系統如圖1所示，其中編碼器和MINE是兩個全連接神經網絡，分別表示調制使用的神經網絡和估計MI使用的神經網絡。編碼器輸入原始比特，輸出調制后的符號；MINE輸入信道兩端的符號，輸出用于估計MI的標量。m為原始比特，輸入編碼器之后進行功率歸一化，得到輸入信道的符號x，x經過信道之后得到有損傷的符號y，將x和y輸入MINE神經網絡，由式(6)計算MI。本文的神經網絡，編碼器擁有3個隱藏層，每個隱藏層有256個神經元，使用Leaky ReLU激活函數；MINE擁有3個隱藏層，每個隱藏層有128個神經元，使用Leaky ReLU激活函數。

圖1 基于MINE的幾何整形系統設計

訓練過程如圖2所示，共訓練L個迭代周期，首先構建編碼器和MINE神經網絡。每個訓練周期中，先生成原始比特，然后根據圖1進行數據正向傳播并且計算MI。訓練編碼器和MINE的目的都是通過式(6)最大化MINE，因此損失函數設置為MINE的相反數。每個迭代周期訓練1次MINE神經網絡，每10個迭代周期訓練1次編碼器神經網絡。

圖2 基于MINE的幾何整形系統訓練流程

2.2 概率整形系統

概率整形是在星座圖的基礎上，通過改變星座符號的出現概率，使得功率低的星座點出現概率大，功率高的星座點出現概率小，從而降低發送信號的整體功率，使得噪聲的功率也隨之下降，起到提高信道容量的作用。通常概率整形在標準方形QAM下進行，不同星座點的概率分布符合MB分布。

圖3 基于MINE的概率整形系統設計

基于MINE的概率整形系統如圖3所示，其中概率生成器和MINE為兩個神經網絡，MINE與2.1節相同，概率生成器輸入固定的數，輸出每個星座點的出現權重，本系統中固定輸入設置為1。將權重經過Gumbel-Softmax激活層[10]得到含有隨機性的不同星座點的輸出概率，Gumbel-Softmax表達式為

式中：α為星座點的權重向量；G為Gumbel隨機數向量；h為通過softmax(柔性最大值)計算得到的不同的星座點出現概率的向量；temperature為溫度常數，當溫度常數接近0時，h接近獨熱編碼分布；當溫度常數接近正無窮時，h接近均勻分布。

每個星座點的概率與星座點所對應的符號相乘，再將所有星座點的結果相加，即可得到概率整形編碼器的輸出符號，然后對符號進行功率歸一化，得到輸入信道的符號x，x經過信道得到有損傷的符號y，將x和y輸入MINE神經網絡，經過式(6)計算MI。概率生成器有兩個隱藏層，每個隱藏層有64個神經元，使用Leaky ReLU激活函數。訓練過程如圖4所示，共訓練M個迭代周期，首先構建概率生成器和MINE神經網絡。每個訓練周期中，首先通過概率生成器生成概率權重，經過Gumbel-Softmax函數激活后與星座點集相乘得到符號，再根據圖3進行數據正向傳播并計算MI。訓練概率生成器的損失函數設置為MINE的相反數。每個迭代周期訓練1次MINE神經網絡，每20個迭代周期訓練1次概率生成器神經網絡。

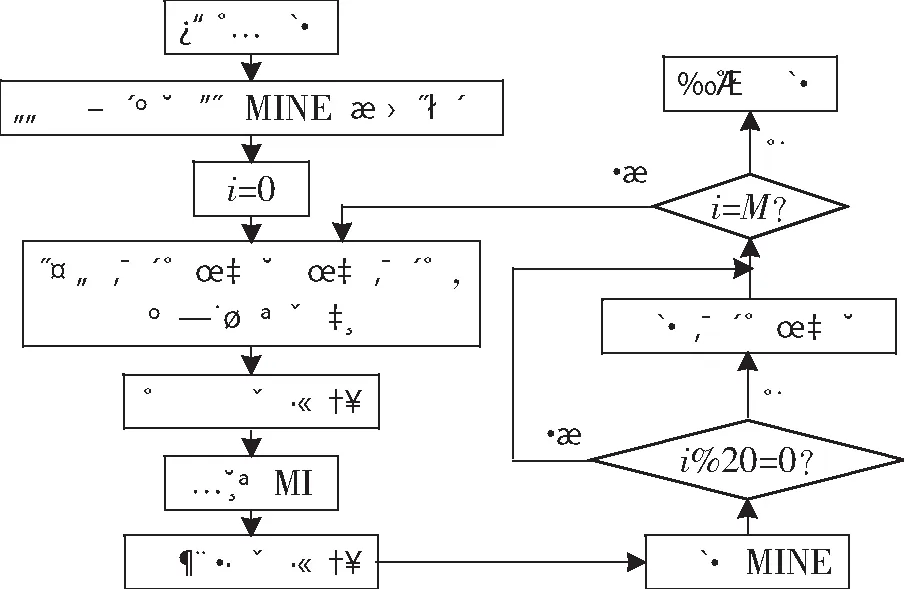
圖4 基于MINE的概率整形系統訓練流程

2.3 幾何與概率聯合整形系統

基于MINE的幾何與概率聯合整形系統的具體訓練流程如圖5所示。首先進行幾何整形和概率整形的預訓練，訓練的方法分別參照2.1與2.2節，其中訓練概率整形所使用的星座圖為編碼器產生的星座圖。訓練結束后計算該狀態下的MI，記為maxMI。

接下來進行迭代的幾何整形和概率整形訓練，即分別訓練系統的編碼器和概率生成器。首先進行幾何整形，先將現有的編碼器模型保存，然后根據不同星座點的概率隨機生成不同數目的幾何整形星座點符號，將這些符號通過信道進行最大化MI的訓練，一次迭代訓練編碼器若干次，在訓練過程中不斷計算新的幾何整形星座圖的MI，如果新的MI比maxMI高，則停止訓練，將新的MI記為nowMI，然后保存新的編碼器模型。如果訓練超過一定次數之后MI一直小于maxMI，則回退到保存的編碼器模型，重新進行訓練。

概率整形的訓練部分，先保存概率發生器模型，訓練概率發生器并且計算MI，超過maxMI則保存MI和概率發生器模型并且停止訓練，訓練超過一定次數則回退概率發生器模型。就這樣訓練，迭代一定次數，保證每次迭代的幾何整形和概率整形的模型的MI都大于上一次的MI。

將訓練周期的總數設置為K，每個訓練周期中，編碼器和概率發生器最多訓練L次迭代，可以保證每次編碼器和概率發生器訓練后，所得新整形系統的MI高于上一個周期的MI。在訓練過程中，系統的MI逐步增加，逼近幾何與概率整形聯合優化的性能極限。

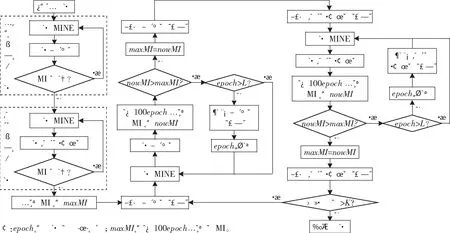
圖5 基于MINE的幾何與概率整形聯合系統設計

幾何整形預訓練設置10 000個迭代周期，概率整形預訓練設置100 000個迭代周期。，暫停訓練并回退模型的閾值設置為2 000，即訓練2 000個迭代周期內，如果編碼器或概率發生器的性能沒有使得系統的信道容量有所提升，就回退并重新進行訓練。在2 000個迭代周期中，前500迭代周期用于預訓練MINE，剩下的1 500個迭代周期中，每100個周期采集一次MI，如果發現新的MI超過了過去的maxMI，則將maxMI更新為nowMI，并且立刻停止訓練。

3 系統仿真與結果展示

3.1 系統仿真設置

為了驗證基于MINE的幾何與概率聯合整形系統的性能，在AWGN信道下進行了仿真驗證，在不同SNR下對QAM、幾何整形、概率整形以及幾何與概率聯合整形的MI進行對比，仿真系統中每個符號對應4位比特。幾何整形系統按照2.1節設置，L設置為20 000。概率整形按照2.2節設置，M設置為100 000。幾何與概率聯合整形按照2.3節設置，K設置為60。計算MI的方法采用蒙特卡洛估計的方式[11]，估計采樣的樣本量足夠多的情況下，這種方式得到的MI是接近精確的。

3.2 仿真結果

基于MINE的幾何與概率聯合整形在不同SNR的AWGN下的整形方案熱力圖如圖6所示。圖中橫坐標和縱坐標分別為信號在I路和Q路的歸一化能量大小，右側坐標軸表示不同星座點的出現概率權重，權重值經過softmax函數計算可以得到星座輸出點的概率。

在熱力圖中，星座點的亮度越高，代表該星座點的權重越高，該星座點發送的可能性越大。在SNR較低，噪聲較大的情況下，中心星座點的概率較高，周圍的概率較低；隨著SNR的升高，周圍星座點的權重逐漸升高，逐漸接近中心星座點的概率。

圖6 基于MINE的幾何與概率聯合整形在不同SNR下的AWGN信道中整形方案的熱力圖

圖7所示為QAM、幾何整形、概率整形以及幾何與概率聯合整形在不同SNR下的AWGN信道中的MI變化曲線。由圖可知，在SNR較低的情況下，所有調制格式和香農極限的MI較接近，由于曲線比較接近，因此選取了SNR=10 dB處的曲線進行放大，由圖可知，幾何與概率聯合整形的系統性能最優，其次是概率整形，再次是幾何整形，16QAM調制相較于星座整形而言性能是最差的。由圖可知，幾何與概率聯合整形的MI相較于概率整形有0.027 9 bit/symbol的增益，相較于幾何整形有0.041 7 bit/symbol的增益，相較于16QAM調制有0.112 6 bit/symbol的增益。與香農極限相比，幾何與概率聯合整形在SNR=10 dB處仍有0.183 4 bit/symbol的差距，但是與16QAM與香農極限間的0.296 0 bit/symbol差距相比，有了較大的性能提升，如果需要繼續提升性能，需要考慮在更高階的調制格式上進行幾何與概率整形。

因此，在AWGN信道中，基于MINE的幾何與概率聯合整形系統可以訓練得到一種性能優于幾何整形與概率整形中任意一種整形方案的編碼方案。在幾何整形與概率整形的基礎上，通過這種方法，可以讓信道兩端的MI更加接近香農極限。

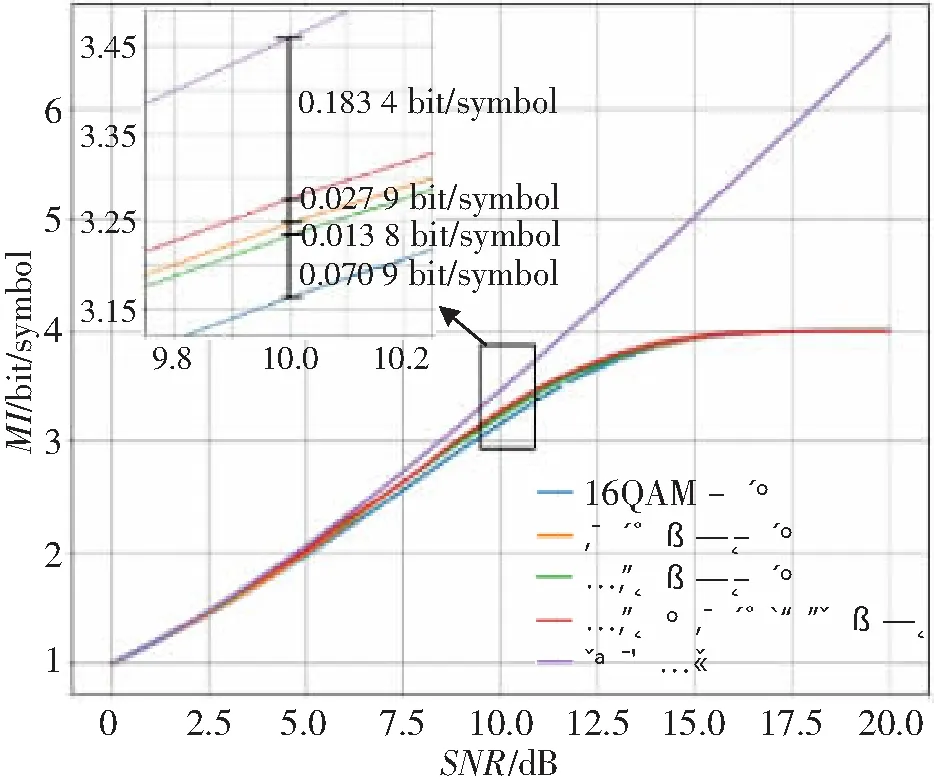
圖7 4種不同編碼方式在不同SNR下的AWGN信道中MI的變化趨勢

4 結束語

為解決QAM在高SNR的情況下，MI與香農極限相差1.53 dB的問題，本文提出了一種基于MI估計的幾何與概率聯合整形的方法，在QAM的基礎上通過星座整形提升系統的MI。本文分別介紹了基于MI的幾何整形、概率整形以及將兩種整形方法聯合訓練的步驟，并且將這套方法在不同SNR下的AWGN信道中進行了仿真驗證。仿真結果表明，幾何與概率聯合整形方法的性能優于單獨進行幾何整形和概率整形中性能。在SNR為10 dB時，系統的MI與單獨做幾何整形相比有0.041 7 bit/symbol的增益，與單獨做概率整形相比有0.027 9 bit/symbol的增益。