增強S形波紋管內壓穩定性分析方法

霍世慧，許紅衛，朱衛平，袁 喆

(1.液體火箭發動機技術重點實驗室，陜西 西安 710100；2.上海大學 上海市應用數學和力學研究所，上海 200072；3.西安航空學院，陜西 西安 710077)

0 引言

波紋管作為一種補償性能良好、使用維護簡單的補償器，在石油、化工、電力、城建和航空航天等領域得到了廣泛的應用。根據實際工作環境的不同，波紋管結構多種多樣，增強S形波紋管是在傳統U形波紋管的基礎上將波峰與波谷間的直線段改為斜線設計而成，并通過增強環的引入使得結構承載能力明顯提升，廣泛應用于航天和核工業等極端高壓工作環境。然而，增強S形波紋管的設計分析相對復雜，理論公式需要經過反復試驗修正，得到的近似公式精度也相對較低，目前仍未形成規律性的成熟經驗。

波紋管在內壓過大的情況下會喪失穩定性，使結構疲勞壽命和位移補償能力大大降低，最常見的失穩模式是柱失穩和平面失穩。柱失穩是指波紋管中心線或軸線整體側向偏移，這是長細比較大的波紋管的常見失穩現象，類似于壓桿的屈曲，其臨界載荷分為彈性和非彈性兩個區域，即表示一系列具有相同直徑、厚度和波形的波紋管發生柱屈曲的臨界壓力值，隨著波紋管長度的增加，曲線從非彈性向彈性過渡。當波數較少或長細比較小時，則易出現一個或多個波紋橫截面發生移動或偏移的現象，即平面失穩，造成這種屈曲的主要原因在于子午向彎曲應力過大，在波峰頂和谷底形成塑性鉸。

圓柱殼在內壓作用下柱失穩的臨界壓力與承受軸向作用均布壓力時相同，這一現象最早由Haringx通過實驗發現，文獻[4-7]等在對C形、Ω形、U形等波紋管整體剛度問題深入理論研究基礎上，對這一現象進行了理論解析證明，為波紋管臨界失穩壓力的計算提供了理論依據。陳曄發現波紋管在內壓和軸向位移的聯合作用下，波谷將首先進入塑性狀態，提出將環板中出現塑性區作為平面失穩的判據。鐘玉平等通過試驗研究證明膨脹節制造商協會標準(EJMA)中的平面失穩極限設計壓力計算方法同樣適用于外壓作用工況，并指出內壓和外壓作用下平面失穩的機理是一致的，同時壓縮位移降低了外壓平面失穩的臨界壓力。文獻[12-13]開展了拉伸及外壓載荷作用下金屬波紋管穩定性的試驗研究和有限元分析，給出了拉伸和外壓載荷下金屬波紋管的臨界載荷。張玉田分別開展了外壓、拉伸及其綜合載荷作用下薄壁波紋管周向穩定性研究。談卓君等開展了多層U形波紋管軸向剛度及臨界載荷的有限元分析，分析中同時考慮波紋管層間接觸條件及波峰到波谷壁厚的變化，并通過與試驗結果的對比，驗證了分析的合理性。文獻[16-17]研究了金屬波紋管的剛度及其流固耦合特性，給出了金屬波紋管流固耦合分析方法。徐學軍等針對增強S形波紋管建立了一種結構耐壓強度分析方法。國內外的研究主要集中在U形金屬波紋管結構的內、外壓和軸向拉伸作用結構極限承載能力的分析和試驗方面，涉及耐高壓增強S形波紋管的研究相對較少，未能形成有效的分析方法總結。

本文將針對增強S形波紋管，結合有限元分析和EJMA相關規范，給出該類型波紋管柱失穩臨界內壓的解析分析方法，為增強S形波紋管的結構設計分析提供依據。

1 增強S形波紋管結構說明

圖1所示為增強S形波紋管，主要包括S形波紋管、增強環和直邊段增強環，增強環直接提高了結構整體的耐壓能力，直邊段增強環位于結構的上下兩端，用于與外部結構的連接。

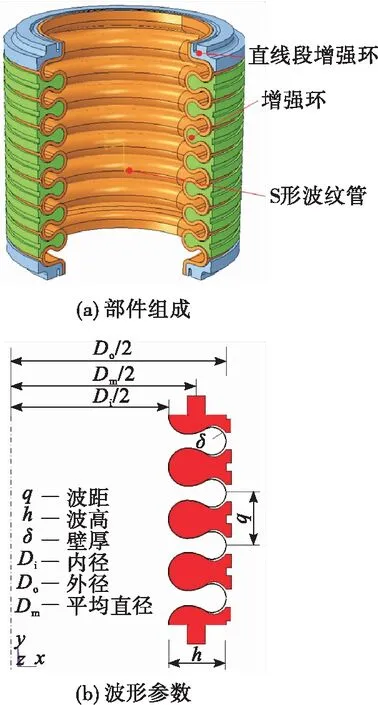
圖1 增強S形波紋管

增強S形波紋管總長127.5 mm，最小通徑80 mm；波紋管波距為14.7 mm，波高為17.4 mm，共含8層薄壁結構，總厚度為2.4 mm。S形波紋管材料為0Cr18Ni10Ti，增強環與直線段增強環材料為S—06鋼，兩種材料力學性能參數如表1所示。

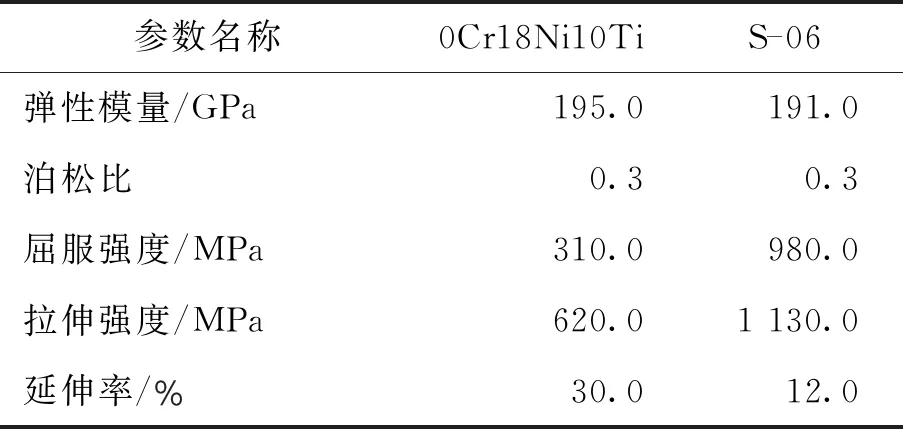
表1 增強S形波紋管材料參數

2 增強S形波紋管穩定性分析方法

波紋管的失穩主要包括平面失穩和柱失穩兩種表現形式。平面失穩是由于應力過大，導致結構在波谷和波峰位置形成了“塑性鉸”，直接影響波紋管的疲勞壽命，但針對增強S形波紋管，增強環對波紋管起到直接保護作用，不可能發生平面失穩現象，因此下面的分析將重點關注增強S形波紋管的柱失穩情況。

柱失穩是指波紋管軸線變彎，中間波紋有較大的橫向偏移，波距發生明顯變化的現象。柱失穩分析主要采用如式(1)所示的Euler公式。

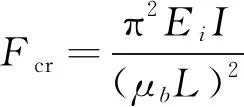
(1)

式中：為波紋管彎曲剛度；為長度折算系數，主要與波紋管端面支撐相關，參考EJMA標準，針對“法蘭等連接件剛度遠大于波紋管管口的剛度”按固支約束條件處理，取=05，并對“帶初始轉角和橫向位移的剛性連接端”或“可轉動和移動的剛性連接端”，引入邊界影響系數=()，其中為連接端最大轉角，單位為rad；為波紋管長度。

設定增強S形波紋管由個波距為的波紋管構成，波紋管平均直徑為，由此可得增強S形波紋管柱失穩的臨界內壓，具體表達如式(2)所示，下面將分別給出增強S形波紋管彎曲剛度和邊界影響系數的確定方式。

(2)

2.1 波紋管彎曲剛度的確定

波紋管彎曲變形過程中，結構一側處于壓縮變形狀態，對應的另一側處于拉伸變形狀態，彎曲剛度的理論解析主要通過軸向拉、壓剛度的等效換算獲得。圖2所示為增強S形波紋管彎曲變形示意，將波紋管等效為長度、平均直徑、壁厚的薄壁圓筒，設圓筒轉角和彎矩的增量分別記為Δ和Δ，軸向位移增量記為Δ=,+1-,(=1,2,…)，由此可得

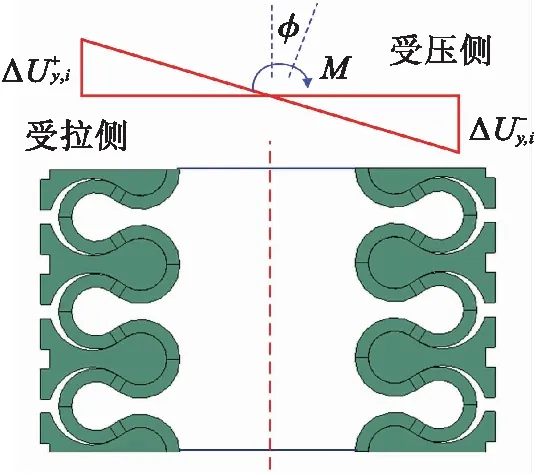
圖2 增強S形波紋管彎曲變形

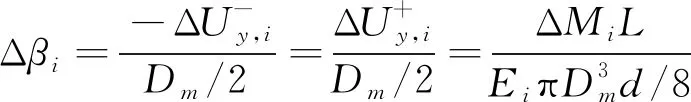
(3)

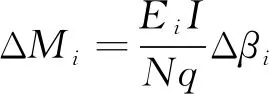
(4)

等效薄壁圓筒彎曲剛度主要通過軸向拉、壓剛度換算得到，其壓縮位移增量和載荷可表示為式(5)和式(6)。

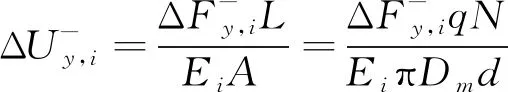
(5)

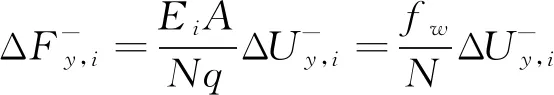
(6)

拉伸位移增量和載荷可表示為式(7)和式(8)。

(7)

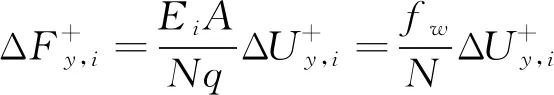
(8)

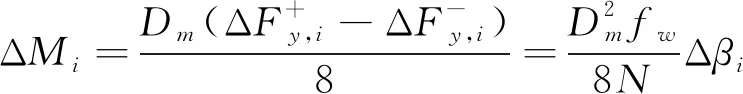
(9)

由式(4)和式(9)可以獲得波紋管整體彎曲剛度表達式如式(10)所示，其中波紋管單波軸向剛度由有限元數值仿真分析結果獲得，至此式(2)中增強S形波紋管柱失穩的臨界內壓可表達為式(11)。

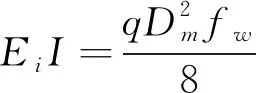
(10)

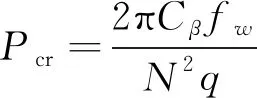
(11)

2.2 波紋管邊界影響系數

內壓作用下薄壁圓柱殼軸線穩定控制方程如式(12)所示。

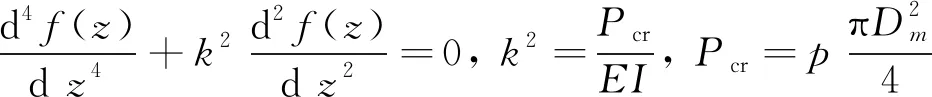
(12)

式中()為軸線撓曲函數，其通解為

()=cos+sin++

(13)

根據式(14)所示轉角方程和式(15)邊界條件，可以解得相關系數如式(16)所示。

′()=-sin+cos+

(14)

(0)=，′(0)=，()=0，′()=0

(15)

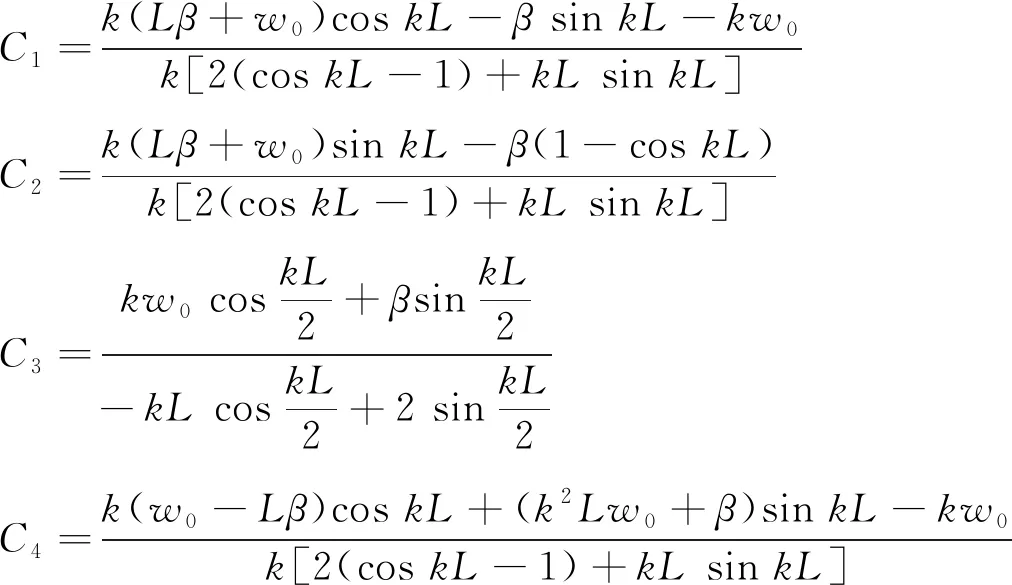
(16)

將式(16)代入式(13)，得到內壓作用下薄壁圓柱殼撓曲度的解。圓柱殼失穩的條件是撓度趨向無窮大，即要求式(16)中至少有一項趨向無窮大，由此可以解得最小臨界壓力如式(17)所示。

(17)

以上求解過程表明，只要是兩端固支邊界條件，按標準的特征值問題求解失穩臨界壓力，所得結果與連接端是否轉動和移動無關。但根據經驗和試驗測試結果分析，EJMA標準認為波紋管承壓后當其波距超過承壓前的1.15倍時，屈曲就已經發生，即實際臨界載荷小于式(17)結果，其減小量就需要通過修正系數來控制。

圓柱殼結構轉動示意如圖3所示，圓柱殼下端面由點轉動至點，圓柱殼轉角為，軸向位移量為。

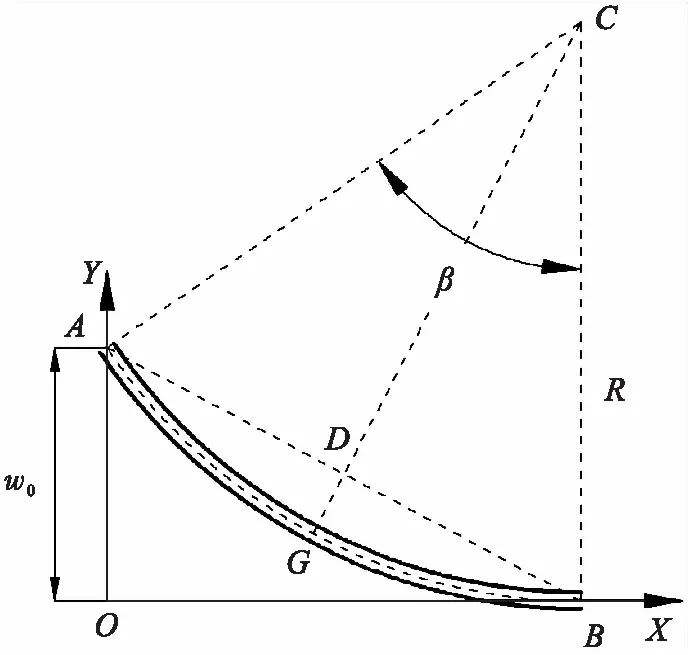
圖3 圓柱殼結構轉動示意

在小位移條件下(=)，機構運動引起的端面轉動與移動的關系如式(18)所示，中點撓度可表示為式(19)。

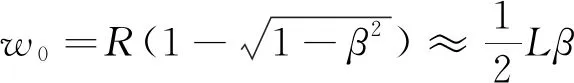
(18)

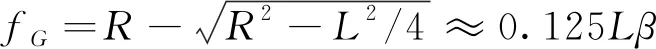
(19)

依據EJMA標準，將波距增加1.15倍(相當于撓曲線轉角增加1.15倍)作為失穩的起點，由此可得中點撓度增量與圓柱殼長度的關系如式(20)所示。

Δ=0125Δ=(2)

(20)

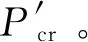
(21)

將式(21)與式(17)相比得

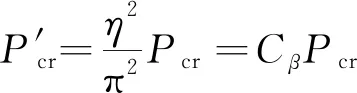
(22)

于是便得到波紋管邊界影響系數的修正值，如式(23)所示。

(23)

3 算例

針對圖1給出的增強S形波紋管開展結構柱失穩最小臨界壓力分析，波紋管工作壓力為35 MPa，搖擺角度為10°，由式(23)確定波紋管邊界影響系數為0.814 2。基于有限元軟件ABAQUS開展增強S形波紋管剛度特性分析，根據波紋管自身結構特點和載荷的對稱性，建立如圖4所示二維軸對稱模型，波紋管材料采用雙線性隨動強化本構關系，模型上端施加軸向約束，下端施加軸向拉伸或壓縮位移載荷，波紋管層間及其與增強環之間均定義為“面-面”接觸關系，摩擦系數選取為0.12。通過施加一定的軸向位移，求出由此產生的軸向約束反力，從而獲得增強S形波紋管結構軸向伸縮力學特性。

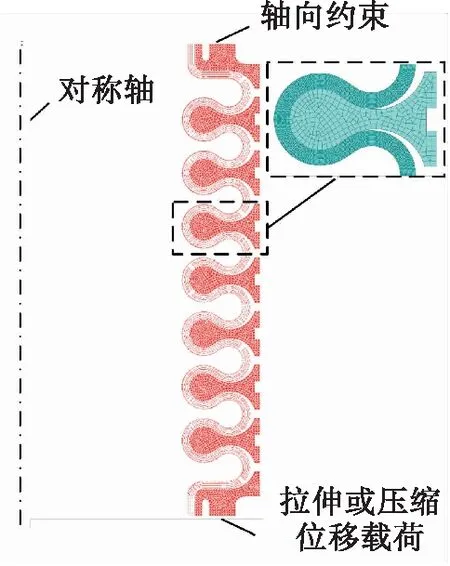
圖4 有限元模型及其邊界條件

增強S形波紋管軸向拉壓曲線如圖5所示，軸向拉伸載荷作用下，增強S形波紋管表現出非線性狀態，初始階段波紋管軸向約束力與拉伸位移的線性度較好，波紋管表現出“高剛度”狀態；隨著拉伸載荷的增大，波紋管局部進入屈服，呈現出軟化的現象，表現出“低剛度”狀態。軸向壓縮載荷作用下，增強S形波紋管的非線性特征更加顯著，表現出強非線性狀態。與軸向拉伸曲線相同，波紋管在進入塑性屈服前，軸向約束力與壓縮位移線性度較好，波紋管表現出“高剛度”狀態，而在進入塑性屈服以后，波紋管呈現出軟化現象，剛度發生下降。但經歷一段“低剛度”狀態后，當波紋管波峰與增強環外側圓弧端面完全貼合時，波紋管達到一種如圖6所示的新的穩定狀態，從而使得壓縮剛度陡增。

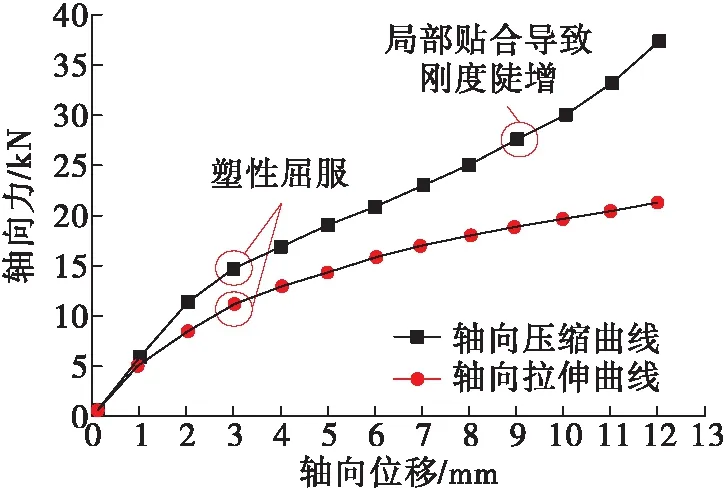
圖5 增強S形波紋管軸向拉壓曲線

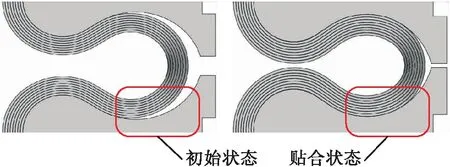
圖6 波紋管軸向壓縮局部貼合狀態

拉伸與壓縮載荷作用下，增強S形波紋管均呈現出非線性特征，在柱失穩臨界壓力的分析中，整體結構彎曲剛度由拉壓剛度的最小值確定。結合有限元分析結果，確定增強S形波紋管單波軸向剛度為12 152 N/mm，代入式(2)獲得搖擺角為10°工況增強S形波紋管柱失穩臨界壓力為70 MPa，安全系數為2.0。波紋管軸向剛度分析中綜合考慮了材料彈塑性、邊界非線性、內壓、大位移和拉壓不對稱等因素的影響，并在臨界載荷分析中引入邊界影響系數，臨界壓力分析方法較為完整地考慮了結構的各種影響因素，因此采用本文提出方法開展增強S形波紋管結構穩定性分析時，柱失穩安全系數不必取得很大。

4 結論

論文針對增強S形波紋管，給出結構柱失穩臨界壓力分析方法，可以得出如下結論：

1)結合增強S形波紋管拉伸和壓縮剛度推導獲得波紋管整體結構彎曲剛度，拉伸與壓縮載荷作用下，增強S形波紋管呈現非線性特征，柱失穩臨界壓力分析中由最小拉壓剛度確定結構彎曲剛度；

2)基于內壓作用下薄壁圓柱殼軸線穩定控制方程和彎曲過程波紋管結構幾何關系，建立增強S形波紋管搖擺過程邊界影響系數的選取方法；

3)綜合考慮材料彈塑性、內壓和邊界影響因素的影響，建立了增強S形波紋管內壓穩定性的分析方法，并給出在典型波紋管結構中的應用。