燃燒組件時域分布參數系統動力學模型

李元啟，趙曉慧，陳宏玉，劉紅軍，劉 上

(1.西安航天動力研究所，陜西 西安 710100； 2.西北工業大學 航天學院，陜西 西安 710072)

0 引言

燃燒組件是液體火箭發動機中重要的核心組件之一，其工作過程包含了流動與燃燒現象中極其復雜的物理化學過程，且工作參數在短時間內變化劇烈。對燃燒室工作過程的建模一直是學者重點研究的方向。特別是在發動機系統動態過程仿真中，既要考慮模型的準確性，又要保證一定的計算速度，使得燃燒室的建模工作極富挑戰性。

早期的研究中，主要關心系統的低頻緩變過程，燃燒室建模采用零維模型，該類模型反映的是參數的平均效應，能夠在低頻范圍內描述燃燒室的建壓過程。劉昆、程謀森等在此基礎上將燃燒室分為燃燒區和流動區，燃燒區采用零維集總參數模型，對流動區和噴管建立一維理想氣體假設下的流動有限元狀態變量模型。劉上等利用線性化頻域法建立了包含零維燃燒區和考慮聲學效應的分布參數流動區的燃燒室模型，分析了涵蓋燃燒室中高頻的動態特性。上述分區模型將燃燒室動態特性的研究范圍從低頻擴充到了中高頻率，但是其流動過程均采用了無源等熵流動的假設，與實際情況存在一定的差別。文獻[9-11]在沖壓發動機燃燒室性能分析時用一維歐拉方程描述燃燒流動過程，可以準確地反映燃燒室內的參數分布情況，但其模型中放熱源項采用燃料熱值與燃料流量的乘積來確定，僅適用于燃料完全反應的富氧工況。火箭發動機燃燒室內存在富燃或富氧的不同工況，該模型并不完全適用。

本文在前人基礎上，基于一維氣相歐拉方程，考慮液體推進劑蒸發加質、化學反應放熱、流動截面積變化，建立了適用于火箭發動機燃燒組件系統動力學仿真模型。

1 數學模型與求解

假設燃燒室截面積是緩慢變化的，其參數的均值僅取決于一個方向的空間坐標和時間，則燃燒室內的物理過程可視為準一維流動和化學反應，在氣相控制方程基礎上考慮橫截面積變化、物質質量添加、化學反應放熱、壁面摩擦和變比熱比等各種影響因素，則燃燒室內的過程可用準一維歐拉方程描述，其中向量方程的3個分量分別代表了質量守恒、動量守恒和能量守恒方程。

(1)

式中：為守恒變量；為通量函數；為源項。其表達式分別為

(2)

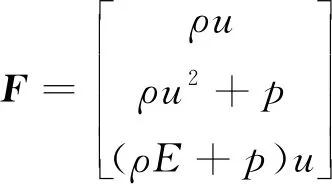
(3)

(4)

(5)

1.1 源項的分析

控制方程中較為關鍵的一項即源項，源項中包含了質量守恒方程的源項、動量守恒方程的源項和能量守恒方程的源項。其中質量守恒方程的源項代表液態推進劑蒸發成氣態，從而給氣相控制方程帶來的加質項。其數學模型可以用蒸發和摻混的子模型來描述。動量守恒方程的源項代表了氣體與壁面的摩擦損失。能量守恒方程的源項代表了氣相推進劑之間化學反應的放熱項以及氣體與壁面熱交換帶來的加熱或放熱項。如何通過各個子模型準確地描述上述物理過程是燃燒室數學建模的關鍵。

加質項可表示為

(6)

其物理意義為假設液態推進劑的蒸發沿燃燒室的分布形態為正弦信號的前半個周期，并且蒸發的范圍限定于區間[，]內，式(6)滿足，即保證了質量添加的守恒性

(7)

釋熱項主要是求反應焓的問題，通過熱力計算可以得到推進劑化學反應的平衡溫度，即

=(,)

(8)

式中：為混合比；為燃燒室壓力。因此反應焓可以表示為

(9)

值得注意的是，混合比以入口的氧化劑和燃料的質量流量的比值來表示[見式(10)]，而不是以燃燒室內總的氧化劑和燃料的質量積存量來表示，因此燃燒室的熱力參數可以敏感地對入口流量的波動進行響應。這樣就解決了一大關鍵問題，即流量的高頻擾動可以實時地被模型所反映，進而反饋到燃燒室的其他熱力參數的計算上。故而該模型能夠本質地適應高頻相應的計算。

(10)

1.2 數值計算格式

空間離散采用了ROE格式，具體格式見文獻[16]。由于存在源項和動量方程中面積變化帶來的附加項，直接采用ROE格式計算會導致在面積變化處產生流量不守恒的現象，需對式(1)的特征向量進行修正，具體形式為

(11)

(12)

(13)

式中符號的含義見文獻[16-17]。

對于火箭發動機而言，燃燒室內蒸發和化學反應的時間尺度非常小，而流動和傳熱的時間尺度較大，即意味著其數學模型存在很大的剛性，顯式的歐拉法或龍格-庫塔法求解剛性微分方程較為困難，因此時間離散采用了隱式變步長的時間推進Dassl方法。

2 算例驗證

2.1 靜態算例

以線性分布熱源的問題為例，模型示意圖如圖1所示。氣體工質為空氣。流通通道為等截面，忽略氣體的摩擦力，對于理想無黏流動，初始時刻加熱量為零，則各個截面上氣流參數相同，入口靜壓=1×10Pa，靜溫=300 K，單位橫截面積上的氣流流量=01 kg/s，管道總長度=0.1 m，管道截面積=001 m，氣流通道內的熱源分布為

圖1 線性熱源問題示意圖

(14)

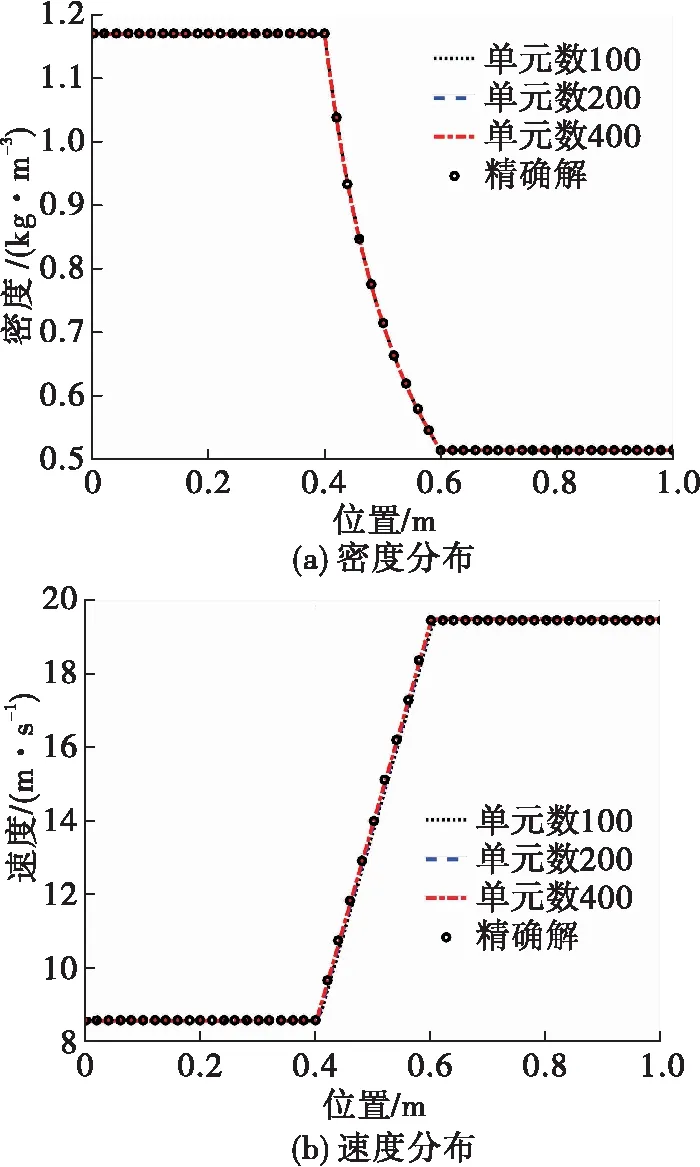
圖2 線性熱源問題計算結果

2.2 動態算例

以文獻[20]中的試驗結果為例，對含熵波和聲波的氣路算例的求解進行驗證。如圖3所示，該試驗裝置是由一段長約1.5 m和直徑0.12 m的圓柱形流動管路組成，流路出口設置短噴管使流動達到臨界音速，冷空氣和熱空氣經過臨界氣噴嘴送入該試驗裝置流路。冷空氣流路噴嘴前設置諧波干擾，使冷空氣產生流量振蕩，進而引起摻混氣體的溫度變化，以形成熵波，增大冷空氣的流量會導致混合氣溫度降低，因此將冷空氣等效為燃料，熱空氣等效為氧化劑。該方案可等效于富燃燃燒室，可以模擬富燃燃氣發生器燃料流路中的干擾。高低溫氣體在頭部處通過很多氣噴嘴直接進行摻混，混合距離可以忽略不計，認為在燃燒室入口處已經完成了混合。

圖3 試驗裝置示意圖

給定入口邊界條件，熱空氣溫度=780 K，流量=684 kg/s，冷空氣溫度=300 K，流量為周期性變化，表達式為

=+Δsin(2π)

(15)

式中,c0=10 kg/s。

分別采用集中參數模型和本文的分布參數模型對該試驗裝置的動態特性進行仿真計算，并將時域解變換至頻域，結果如圖4所示，結果表明，在=0～600 s的低頻范圍內，氣路的幅值響應有逐漸降低的趨勢，即對低頻幅值響應更敏感，相位差滯后隨頻率的增加有增加的趨勢，在100 s以上的頻率范圍，在幅值和相位特性上均產生了熵波響應。

圖4 試驗裝置末端的頻率特性

從幅值上看，本文的分布參數模型和集中參數模型均和試驗結果吻合較好，區別在于，集中參數模型不能捕捉到100 s以上的熵波現象，而分布參數模型完全能夠反映出熵波現象。再從相位上看，集中參數模型在大于100 s的范圍內，完全和試驗結果相背離，而分布參數模型與試驗結果能夠吻合，再次驗證了集中參數模型只能適用于低頻范圍內，=100 s對應的頻率為100/2π，即不到20 Hz。這與文獻中提到的頻率范圍相一致。而本文提出的分布參數模型所適用的頻率范圍遠大于集中參數模型。

進一步地，將研究的頻率范圍擴充至中高頻范圍，取無量綱角頻率0<<8，計算氣路的頻率特性，并與試驗數據比較，圖5為氣路試驗系統管路末端的壓力頻率響應特性，圖6為氣路試驗系統管路中點位置的壓力頻率響應特性。

圖5 氣路試驗系統管路末端壓力頻率響應特性

圖6 氣路試驗系統管路中點壓力頻率響應特性

結果表明，在更高的頻率范圍內，采用集中參數模型計算的壓力響應幅值趨向于0，說明了集中參數模型無法反映高頻的響應特性。而分布參數模型和試驗結果吻合較好，特別是在=π的位置，即一階縱向聲學頻率處，氣路的末端應處于壓力振蕩的波腹位置，振幅最大，氣路中點處應處于壓力振蕩的波節位置，振幅最小。本文的模型準確地捕捉到了氣路末端的壓力響應峰和氣路中間的壓力波節，峰值和頻率均與試驗結果吻合。甚至到了二階聲學頻率處(=2π位置)，該模型也有較好的計算結果，二階聲學頻率下氣路的末端和中點均為壓力振蕩的波腹，振幅最大，模型的計算結果和試驗結果也能夠吻合。從相頻特性曲線上看，當入口流量的擾動頻率增加時，氣路中點和末端與入口的相位角滯后是逐漸增大的，相對而言，氣路末端的相位角滯后相對更大，可以看到，分布參數模型對相位角的計算與試驗結果也能較好吻合。

在低頻范圍內試驗數據表明了氣路中存在明顯的熵波波動特征。但在無量綱角頻率>1.5后，試驗數據沿著比較平滑的曲線移動，這一點在相頻曲線中體現得更加明顯。這是由于熵波是一種物質波，其傳播速度等于流速，文獻[20]提到，在通常湍流度水平的圓柱形流路中，當頻率大于400 Hz時，熵波會產生耗散效應。原因在于，熵波的產生機理是：當入口推進劑流量產生波動時，在燃燒室內會周期性地生成溫度不同的燃氣團，當擾動頻率較低時，前一時刻生成的燃氣團有足夠的時間向下游流動，后一時刻在燃燒室頭部生成新的燃氣團時，前一時刻的燃氣團已經流向了下游，各個溫度不同的燃氣團存在位置空間上的分布，氣團隨流體整體向下游流動，從而造成了燃燒室內的壓力波動。當入口擾動頻率很高時，上一個時刻生成的燃氣團還沒來得及流動到下游，又在同一個位置生成了另一個燃氣團，高低溫的燃氣團幾乎在同一位置生成，進而迅速達到熱平衡，使得燃氣溫度在空間分布趨于平均效應，因此無法形成壓力波動。在表象上熵波表現出了高頻耗散效應，即在低頻下，燃燒室的壓力響應曲線上會疊加熵波響應，而在高頻下，壓力響應曲線不會疊加熵波響應，壓力幅頻響應曲線應趨于平滑。

與文獻[8]中的燃燒室線性化頻域模型相比較，見圖5和圖6。線性化頻域模型在高頻下仍存在疊加的熵波，在相頻特性曲線上尤為明顯，與上述物理過程不相符合。而本文所建立的時域非線性分布參數模型計算得到的響應曲線在低頻處存在熵波疊加，在高頻處趨于平滑，能夠準確地捕捉到高頻下的熵波耗散現象。原因在于，在時域的控制方程中，已經考慮了速度、壓力和溫度等參數之間的耦合關系，其傳播和耗散特性已經在方程中得以體現。因此，只要差分方程和微分方程滿足相容性關系，數值積分計算的結果就能夠反映原有的物理特性。

3 結論

1)建立了時域上的非線性分布參數燃燒組件動力學模型。將空間從零維擴充到一維，所研究的頻率范圍從低頻擴充到中高頻(涵蓋一階縱向聲學頻率)。

2)靜態算例的計算表明，數值仿真結果和精確解能夠較好吻合。驗證了模型對燃燒組件靜態流場與溫度場求解的準確性。

3)含熵波和聲波的氣路算例驗證結果表明，模型結果和試驗測量結果吻合較好。本文所建立的模型既能準確捕捉到高頻的聲波特征和低頻的熵波特征，又能準確反映高頻下的熵波耗散特征。