卷積式的拓方運算及其應用

劉智全

（唐山市豐潤鎮中學，河北 唐山 064000）

1 引言及預備知識

在文獻[1]給出的卷積式基礎上，提出了卷積式的拓方運算，研究了其運算性質，進而提出了高次組合數及相關公式.運用該運算及一些數學方法和技術[2-9]，解決了若干個多項式積的展開問題及2 類Stirling數的卷積式表示問題.文中相關符號含義見文獻[1-2].

m×(n+1)型卷積式指的是項的和，這些項取自其中的不同行，每一項的形式為a1j1a2j2…amjm，且j1+j2+…jm=n.

定義（卷積式的拓方）用符號表示卷積式的r（r為整數）次拓方，其滿足條件：

（1）當r≤1 時，，并且約定當r＜ 1-n時，A的r次拓方恒為零.

（2）當r＞1 時，

由卷積式拓方的定義可知，某卷積式的一次拓方是原卷積式本身，卷積式拓方后仍是一個卷積式，卷積式的性質在其拓方中均成立.

2 卷積式拓方的運算性質

定理1

證明由卷積式拓方的定義，有

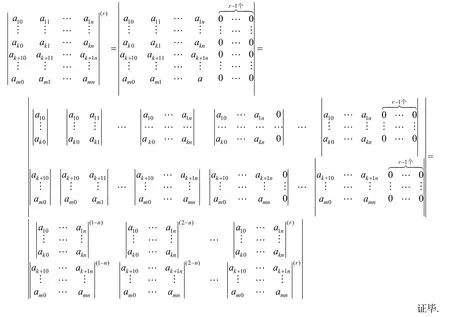
由定理1 可得到定理2.

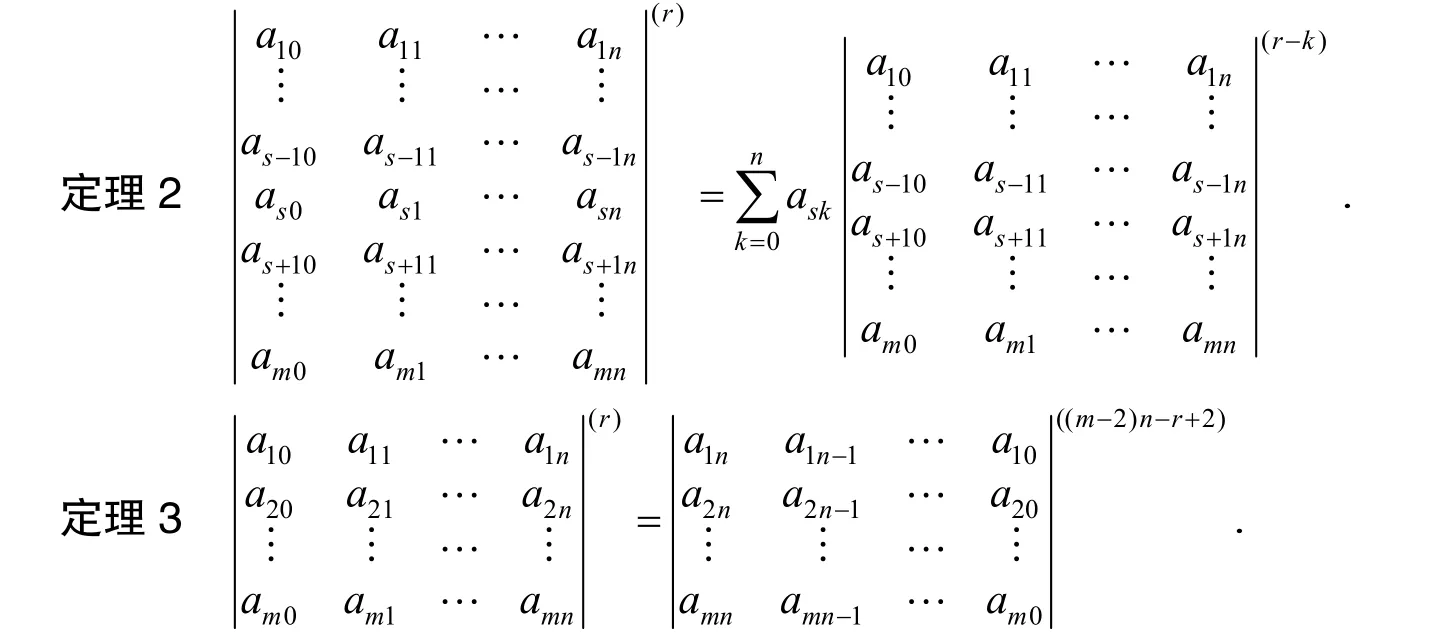
證明對行數m作數學歸納法.容易驗證，m=1,2時命題成立.假設m=k時命題成立，即

當m=k+1時，由定理2 及歸納假設可知，，即m=k+1時命題成立.

定理4當r＞ (m-1)n+1時，

使用歸納法可證明定理4.由定理3～4 易見卷積式拓方定義中的約定是合理的.

當n=1 時，的一個特例.

由卷積式及其拓方的定義不難得到定理5.

定理5卷積式A的r次拓方是項的和，這些項是取自A的不同行的m個元素的乘積，每一項的形式為a1j1a2j2…amjm，j1+j2+…jm=n+r-1.

3 卷積式及其拓方的應用

3.1 若干個多項式的乘積

文獻[1]中應用卷積式成功解決了若干個冪級數的乘積展開問題，在此基礎上再應用卷積式及其拓方的有關知識不難得到關于若干多項式積展開問題的相關定理.

應用定理6 可將任意的幾個多項式的積直接展開成一個新的多項式.

例求的展開式.

解由定理6 可知，

3.2 2類Stirling 數的卷積式表示

令t表示任意實數，則階乘函數的定義為(t)0=1,(t)n=t(t-1)…(t-n+1)(n≥1).分別用s1(n,k),s2(n,k)表示第一類Stirling 數和第二類Stirling 數，它們滿足：(t)0=(t)0=s1(0,0)=s2(0,0)=1，

利用卷積式的有關理論及其相關結果可將2類Stirling 數分別用不同形式的卷積式表示出來.

引理1

證明當n≥m-1時，有

應用卷積式相關性質、計算定理，按照上述方法一直做下去，就可以得到

同樣地，應用卷積式的相關計算定理不難計算出當n＜m-1時，卷積式的值為零. 證畢.

由定理5 可得到引理2.

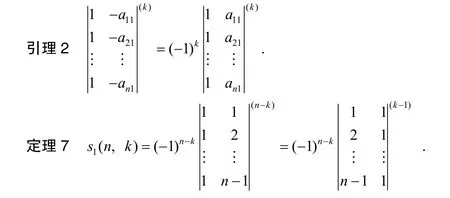
證明由第一類Stirling 數的定義，依次運用定理6、定理3 和引理2 可知，將此式與比較可知，.證畢.

定理8（卷積式的行數為k）.

證明因為，，由引理1可知，，又因為證畢.