基于變形數據的古塔數學建模

秦春影

（南昌師范學院 數學與信息科學學院，江西 南昌 330032）

古代建筑具有很強的歷史和科研價值，今天很多的研究都需要借助古代建筑作為輔助，如一些史實的驗證，古文明的發展過程和歷史等.古塔因其特殊的結構和作用而更加寶貴，流傳至今的古塔的保護十分重要，而充分了解古塔當前的狀態是有效保護的前提條件.流傳至今的古塔受限于當時的科學技術和建筑手段，或多或少存在一些問題[1-4]，如塔基所在地質的不穩定，這種情況下的古塔想保存下來非常不容易.對古塔的損害最常見的是地基的不均勻沉降，從而導致塔體傾斜甚至扭曲[5-6]；還有就是人為破壞（如戰爭等）和自然災害[7]所導致的損壞，這些不同類型的破壞對古塔本身都會造成不同程度的損害，有些損害是不可修復的，還有些損害是可以修復的，或者說可以減緩對塔的損害.近年來，古塔的修復和保護工作受到社會的廣泛關注和重視，但是古塔的修復工作是一項系統性的工作，本身的復雜性遠遠超出外界的想象，修復和保護的方法不科學甚至會加劇古塔的破壞，加快古塔的消亡.本文通過對已有數據的分析，對古塔各層的缺失數據進行合理的填補和恢復，在此基礎上對各層的中心進行定位，從而判斷古塔本身隨著時間按何種趨勢發生變化，為古塔的保護和修復提供科學依據.

1 古塔缺失數據的插補

古塔的層中心對于古塔的修復和積護非常重要，但是由于年代久遠，導致造成數據缺失較為嚴重.如何在包含缺失數據的情況下確定古塔的層中心是本研究關注的核心問題，而這里面最關鍵的問題之一就是對缺失數據的填補或恢復[8-10].以某古塔為例，收集到1986 年7 月，1996 年8 月，2009 年3 月和2011 年3 月對該塔的4 次測量數據，部分測量數據見表1.該古塔一共有13 層，表1 中只是提供了1986 年和1996年的第1 層的數據，共測量了8 個點的數據，其中x，y，z分別為每個測量點的坐標，每一年的測量數據中還包括塔尖的4 個測量點的數據，限于篇幅，其余各層的數據以及2009 年和2011 年的數據不再列出.

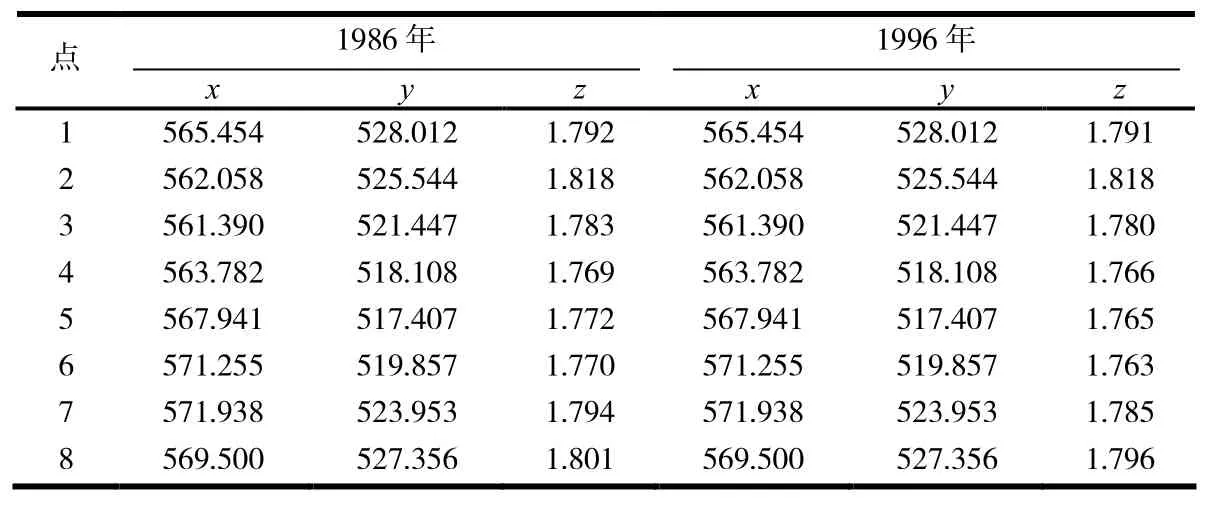
表1 1986 年和1996 年第1 層的觀測數據

由于所給出的數據中缺少1986 年和1996 年第13 層的第5 個測量點的數據，缺少2009 年和2011 年塔尖的第2，3，4 個測量點的數據，因此，需要對缺失的數據進行處理.

對于1986 年和1996 年第13 層第5 個測量點的缺失數據，數據處理的出發點是：每一層的第5 個測量點之間應該具有某種關系，分別繪出前12 層的第5 個測量點各個坐標的散點圖，發現y坐標、z坐標分別近似在一條直線上，因此，可以做出假設，即第13 層的第5 個測量點的y坐標、z坐標也應該分別在各自的直線上.x坐標雖然不是在一條直線上，但是也可以通過類似的方法得到.這樣就可以得到1986 年和1996 年的第13 層的缺失數據（見表2）.

表2 1986 和1996 年第13 層補充缺失后的數據

對于2009 年和2011 年塔尖的第2，3，4 測量點的缺失數據，數據處理的出發點是：因為塔尖相對來說是面積比較小的一塊區域，所以可以假設這塊區域的各個測量點之間的相對位置不會隨著時間的變化而變化，即各測量點之間的相對位置是固定的.通過這種思路可以得到2009 年和2011 年塔尖的缺失數據，補充的缺失數據見表3.

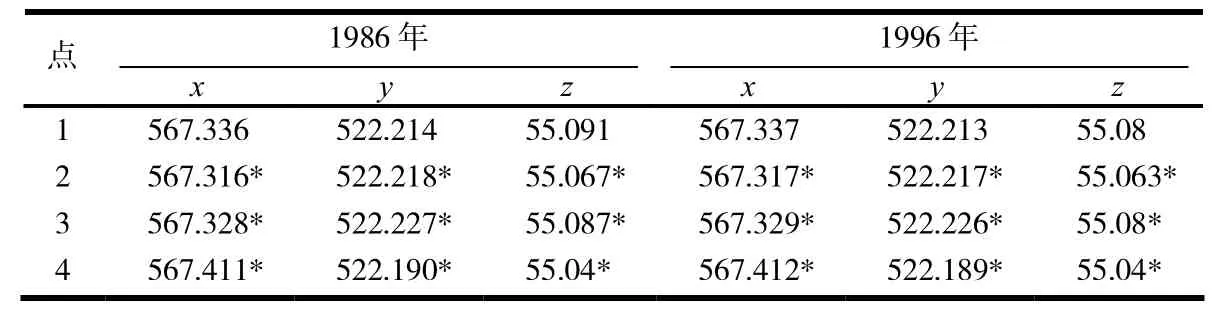
表3 1986 和1996 年塔尖的數據

在對缺失數據補充完整后，可以繪出該古塔的三維立體圖，1986 年該古塔的三維立體圖見圖1.

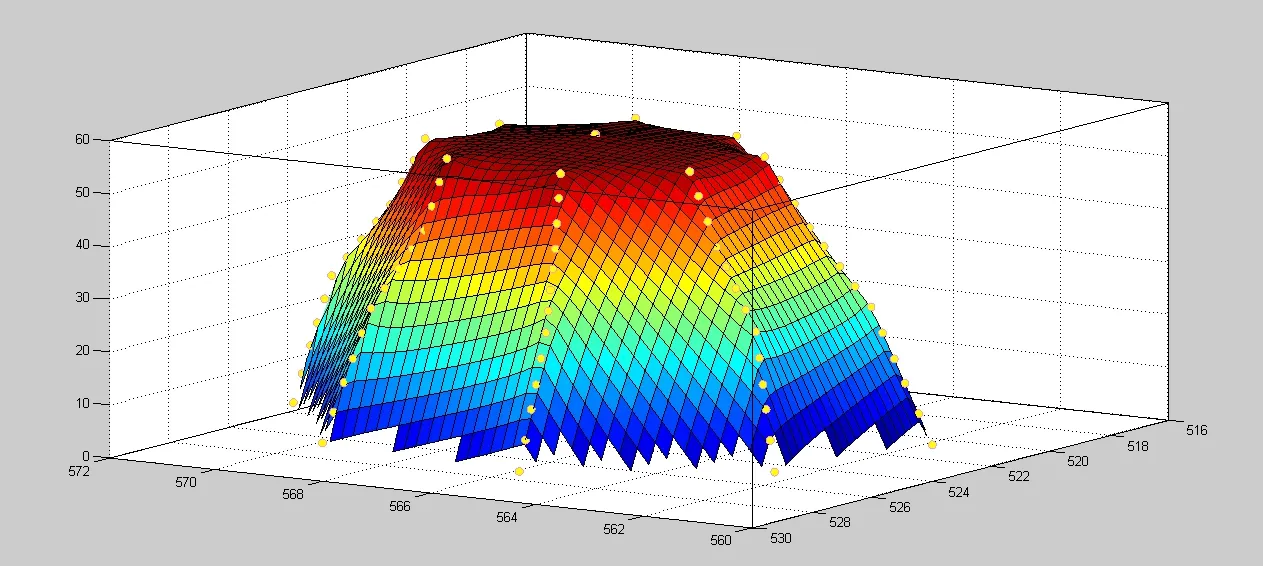
圖1 1986 年該古塔的三維立體圖

由圖1 可以看出，每一層的8 個測量數據正好可以看作是古塔的8 個頂點，該古塔的每一層都是一個八邊形.對于每層層中心的計算問題，首先，假設該古塔是由均質的物質建成的，這樣才可能計算出該塔各層的中心；其次，通過對數據的分析可以發現，每一層8 個點的z坐標很接近，因此假設這8個點是處在同一平面上，這樣各層中心的計算問題就轉化為計算由8個點構成的八邊形的中心問題.由于這8個點構成的平面可能不是正八邊形，因此，不能直接運用正八邊形的中心計算方法，這里考慮采用不規則平面圖形的中心計算方法.

2 古塔層中心的計算

根據平面解析幾何相關的知識可知，如果三角形是由均勻材料做成的，那么幾何中心也就是質量中心.它的中心坐標是3個頂點的坐標算術平均值.也就是說，如果頂點a，b，c的坐標分別為（x a,ya），（x b,yb），（x c,yc），那么該三角形的幾何中心的坐標為

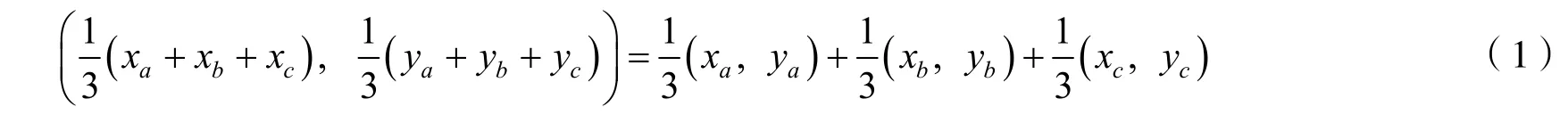
根據假設，古塔是由均勻材料構成的，因此可以使用式（1）來計算中心.

這里每一層測量了8 個點，由這8 個點構成的八邊形可以看成是由幾個簡單基本圖形組合而成的，在計算它們的中心時，可先將其分割為幾塊基本圖形，計算機出每塊圖形的形心位置（x i,yi）與面積Ai，然后利用形心計算公式求出整體的中心位置.

不規則平面圖形的中心坐標公式為

通過對數據的分析可以發現，每一層上的8 個點的坐標按順序連接可以連成一個八邊形.以1986 年第1 層數據為例進行說明（其它各年、各層的數據可以按類似的方法來處理）.1986 年第1 層8 個點的投影圖見圖2.

圖2 1986 年第1層8個點的投影

將這個八邊形進行分割，分割的圖形是由6個三角形構成，這樣，就可以按照前面介紹的方法來計算各層的中心.

圖3 分割后的1986 年第1 層8 個點的投影

分別計算出這6個三角形的中心，然后利用式（1）將這個中心進行合成，合成得到的坐標即為整個圖形中心的坐標.

設8個點的坐標分別為（xi,yi）,i=1,2,…,8.先計算出6個三角形的面積，若已知3個頂點的坐標（xa,ya）,（xb,yb）,（xc,yc），則三角形的面積計算公式為

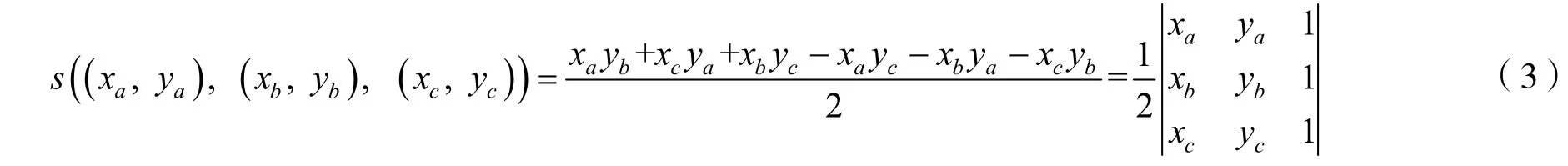
根據式（1）（3）計算出各個三角形的中心坐標和面積，然后利用式（2）對6個三角形的中心進行合成得到各層的中心坐標（x,y,z），其中各層的中心坐標中z值取8個點z坐標的平均值.

1986 年各層的中心和塔尖的中心坐標見表4，其余年份的各層的中心及塔尖的中心坐標可以使用相同的方法計算得到.

表4 1986 年各層的中心坐標

通過這種方法，建立起相應的數學計算公式，在適當的假設條件下，只要給出每層的8個測量點的坐標，編制程序，就可以直接計算出每層的中心坐標.

在解決了確定古塔各層中心的基礎上，接下來就根據各層的中心及塔尖中心的偏移情況來計算整個塔身的傾斜、扭曲和彎曲等情況.假設在理想狀態下，古塔的各層中心是在一條垂直的直線上，如果隨著時間的變遷，古塔各層的中心還在一條直線上，但是這條直線與垂線有一個夾角，這種情況古塔就是發生了傾斜，夾角越大，傾斜越嚴重；如果古塔各層的中心組成了一條類似于C 形的曲線，則古塔發生了彎曲；如果古塔各層的中心組成了一條類似于S 形的曲線，則古塔發生了扭曲，當然，這只是直觀上的分析，具體要判斷古塔到底發生了何種變形[11-13]，還需要借助數學上相應的評價指標來判斷.通過對古塔的變形，可以預測未來古塔的變形趨勢，在此基礎上，可以提出對該古塔的修復和保護方案.

3 結語

通過對古塔不同年份測量數據的分析，在一定的假設基礎上，對缺失的數據進行了相應的處理.古塔各層測量數據中的缺失數據處理是重要的步驟，如果缺失數據部分處理不好或者不處理直接刪除，都會給整個分析的準確性帶來較大的損失，進而影響到古塔當前狀態及變形趨勢的預測，對提出古塔的修復和保護方案產生負面影響[14-15].另外，各層的中心計算是在必要的假設之上的，合理和必要的假設對于數學建模問題的解決也是很重要的[16].因此，對于古塔變形狀態的分析必須充分考慮實際情況和測量數據的特點來綜合考慮分析方案，這樣分析的結果才能對古塔的修復和保護真正起到參考作用.