基于直覺模糊信息的地下儲氣庫安全性可拓評價模型研究

畢傲睿，沈 超，朱洪云，張永成，江 松

(1.淮陰工學院管理工程學院，江蘇 淮安 223003；2.淮陰工學院江蘇省智能工廠工程研究中心，江蘇 淮安 223003；3.西安建筑科技大學資源工程學院，陜西 西安 710055)

提升天然氣儲備能力是近年我國重大的戰略需求，由于地下洞室具有容量大、儲氣成本低以及使用便利等特點，應用地下洞室進行天然氣的存儲逐漸成為國內外青睞的儲能方式[1-2]，地下儲氣庫已成為我國輸氣干線系統極其重要的組成部分[3]。

近幾十年國內外地下儲氣庫的運營經驗和事故表明，地下儲氣庫的有效運營與其安全性因果關聯[4-5]，地下儲氣庫安全性指標的缺陷將造成天然氣泄漏[6]、地表沉陷[7]等，導致儲氣庫運營失效。因此，需要針對地下儲氣庫的安全性進行分析與評價。目前國內外學者針對地下儲氣庫安全性的研究主要集中在對地下儲氣庫性質進行模擬，或對安全性指標的負面作用進行分析。如Staudtmeister等[8]最早采用結構分析數值法研究了鹽巖與時間相關的一些特征，并將結果應用于地下儲氣庫外形和邊界條件的評估中；Zhang等[9]研究了地下儲氣庫的注采流動規律對儲層孔隙度和滲透率變化的影響，提出在注采過程需要改善滲流條件以保證地下儲氣庫的安全；井文君等[10]通過FLAC3D對地下儲氣庫腔體影響因素進行了數值分析，提出了地下儲氣庫腔體體積收縮率的計算方法；李文婧等[11]基于熱力學理論，推導出了地下儲氣庫注采變化導致的溫度和壓力對腔體拉伸損傷影響模型等。而目前鮮有針對地下儲氣庫安全性綜合定量決策方面的研究，主要原因是地下儲氣庫安全性指標較多，樣本信息稀缺，統籌分析的難度大。而對于多指標綜合分析，可拓理論的提出有效降低了處理相關問題的復雜度。如Wang等[12]針對煤層的45個風險指標，基于可拓方法開展了煤炭開發的風險評價和實際應用分析；Tan等[13]應用可拓評價模型并結合經濟、環境和社會多元素，開展了風電場最優選址方法的研究；王新民等[14]利用可拓理論和層次分析法，建立了巖質邊坡穩定性的綜合評價模型；高崇陽等[15]為了減少電力建設事故，基于大量的工人調查數據構建了安全心理過程的可拓優度風險評價模型，實現了一線工人心理過程的有效評估；虞未江等[16]基于感官、化學、毒理學等多元因素，引入物元可拓模型實現并應用于地下水水質的安全評價。同時，對于信息缺乏問題，目前業已成熟的模糊理論可以間接地實現主觀條件下的信息擴展，解決樣本信息含量不足的問題。如范英等[17]提出利用三角模糊數來解決風險評價中存在的單值評價偏差較大的問題；曲昌盛等[18]利用梯形模糊數來處理水質檢測數據，用于降低地下水健康評價中的不確定問題。

基于上述研究，為了使評價結果更加具有工程管理參考價值，本文在地下儲氣庫安全性指標和評價等級的基礎上，應用物元可拓法構建地下儲氣庫安全性可拓評價模型，針對地下儲氣庫參數信息的小樣本特性采用直覺模糊理論進行指標賦權，并引入安全性級別變量特征值實現地下儲氣庫最終安全性的定量評價。

1 基于直覺模糊信息的指標權重計算

地下儲氣庫屬于高投資、長壽命的大型工程項目，獲取高可信度和大量參數信息的成本和難度較大，因此對地下儲氣庫安全性的評價指標通常需要借助主觀經驗進行評判，所以不可避免地會產生信息上的模糊性。但這些模糊性信息在某一標準內必存在相應的界限，可以通過一定方式實現信息的最大化利用。本文采用直覺模糊理論對這種模糊性信息進行處理，以直覺模糊數的形式表現地下儲氣庫安全性指標的主觀評價信息。直覺模糊數除了有正面和負面的信息外，還考慮了猶豫面的影響，這種形式更加有利于對模糊信息的正確分析[19]，在此基礎上對安全性指標權重進行計算。

直覺模糊集的基本定義[20]如下：設U為一個非空集合，稱A={(x,μA(x),vA(x))|x∈X}是U上的一個直覺模糊集。其中，μA(x):X→[0,1]，vA(x):X→[0,1]，且0≤μA(x)+vA(x)≤1 ，x∈U。稱〈μA(x),vA(x)〉為x在A中的直覺模糊數，μA(x)表示x對集合A的隸屬程度，vA(x)表示x對集合A的非隸屬程度。πA(x)=1-μA(x)-vA(x)稱作x是否屬于A的猶豫度(或不確定性)[21]。

通過專家評價構造指標的直覺模糊評價值，進而得到針對地下儲氣庫安全性的評價矩陣。設有n個專家參與評審m個評價指標，專家的評價矩陣Pnm表示為

(1)

式中：pik=〈μik,vik〉表示第i個專家對第k個評價指標的評價值。

若x，y是兩個直覺模糊數，即x=[μp(x),vp(x)]，y=[μp(y),vp(y)]。令λp(x)=μp(x) -vp(x)，λp(y)=μp(y)-vp(y)，則x，y的相似度[22]可表示為

(2)

對任意安全性評價指標Ik，根據相似度可形成所有專家對評價指標Ik進行評審的相似度矩陣：

(3)

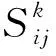
S表示的是所有專家對安全性評價指標相似度的一種衡量。則每個專家對評價指標Ik的相對一致性值為

(4)

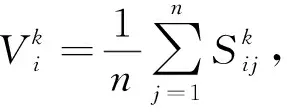
則n個專家對m個評價指標的相對一致性衡量矩陣D可表示為

(5)

矩陣D反映的是各專家對評價指標好或者差的趨勢度量，將所有專家對評價指標Ik的評價態度進行整體性綜合計算，有：

=[μk,vk]

(6)

式中：pk表示所有專家對評價指標Ik的評價值。

最后可定義指標權重為

w(k)=μk+(1-μk-vk)/2

(7)

w(k)包含專家對評價指標Ik肯定的部分和猶豫信息中肯定的部分，由公式(7)可知本文選擇猶豫信息中一半肯定。

2 地下儲氣庫安全性可拓評價模型建立

可拓學是用形式化模型討論事物的規律，并用于解決矛盾問題的理論[23]。基于可拓學理論的地下儲氣庫安全性評價的思路為：利用可拓學理論去分析地下儲氣庫安全性的影響指標，建立具有關聯性的物元模型，進而實現對地下儲氣庫安全性最終的綜合定量評價。地下儲氣庫安全性評價的具體流程如下：

2. 1 確定待評物元

物元就是把待評價對象、特性和對應的衡量值組成一個整體來研究，可表示如下：

Ri=(Ni,Ci,Hi)

(8)

式中：Ri表示物元，i為物元序號；Ni為待評價對象；Ci={ci1，ci2，…，cij}為Ni下的特性集合；Hi={hi1，hi2，…,hij}為對應特性集合的取值。

對于地下儲氣庫安全性，Ni即為指標集，cij和hij分別為指標集下的指標和具體值。

2. 2 確定經典域和節域

經典域是物元中事物特性隸屬于某評價等級的量值范圍，節域是事物特性對應的總量值范圍，分別可表示如下：

Ri(m)=(Qm,Ci,Hm)

(9)

RE(i)=(Ei,Ci,He)

(10)

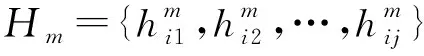
2. 3 計算指標關聯度

關聯度分為單指標關聯度和多指標綜合關聯度。本文中單指標關聯度是對地下儲氣庫安全性指標與評價級別關聯程度的度量，具體計算方式如下：

(11)

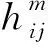
(12)

(13)

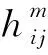
進一步地，多指標的綜合關聯度是對評價對象的整體性質與各評價等級關聯程度的度量，可表示如下：

ks=∑wijkm(cij)

(14)

式中：ks為多指標綜合關聯度，s=1,2，…，i；wij為指標cij的權重，由公式(7)確定。

在ks中，最大的max[ks]所屬的等級為評價對象的評價等級。

2. 4 確定安全性級別變量特征值

由max[ks]確定的安全性評價等級過于粗糙，有時需要進一步了解定量評價的趨勢，以便更好地進行決策。可以通過安全性級別變量特征值來體現這種趨勢，安全性級別變量特征值s′由下式計算：

(15)

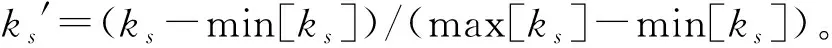
綜上可知，對于地下儲氣庫的安全性評價，需先確定待評物元、經典域和節域，再結合專家給出的指標直覺模糊評價信息計算指標的權重和關聯度，最終可得到定量表示的安全性級別變量特征值，具體評價流程見圖1。

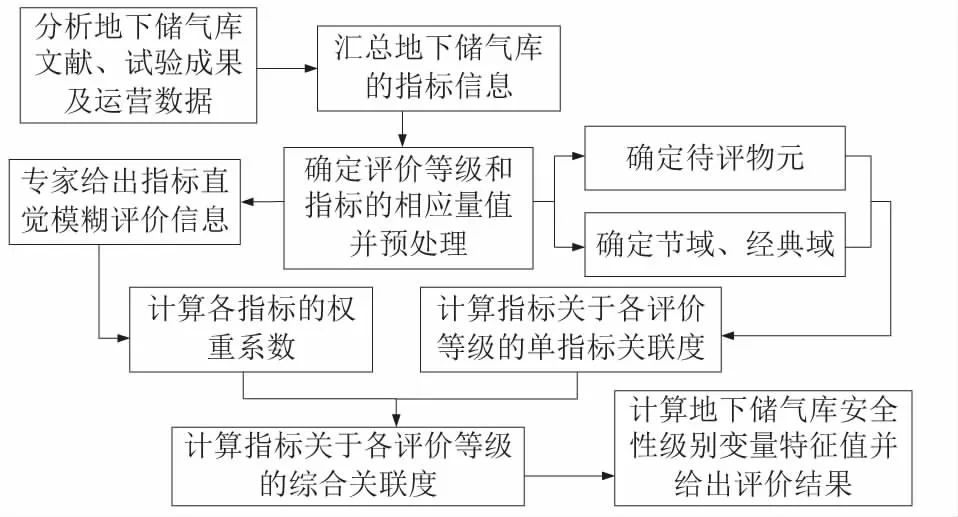
圖1 地下儲氣庫安全性評價流程Fig.1 Flow chart of security evaluation

3 實例應用與分析

江蘇金壇某地下儲氣庫已運行十年以上，現因制定維護決策需求對其進行安全性評價。

該地下儲氣庫位于金壇盆地西部，中間部分為巖鹽，頂部和底部主要成分為泥巖，含部分泥巖夾層，地下儲氣庫地層分布及剖面示意圖見圖2。

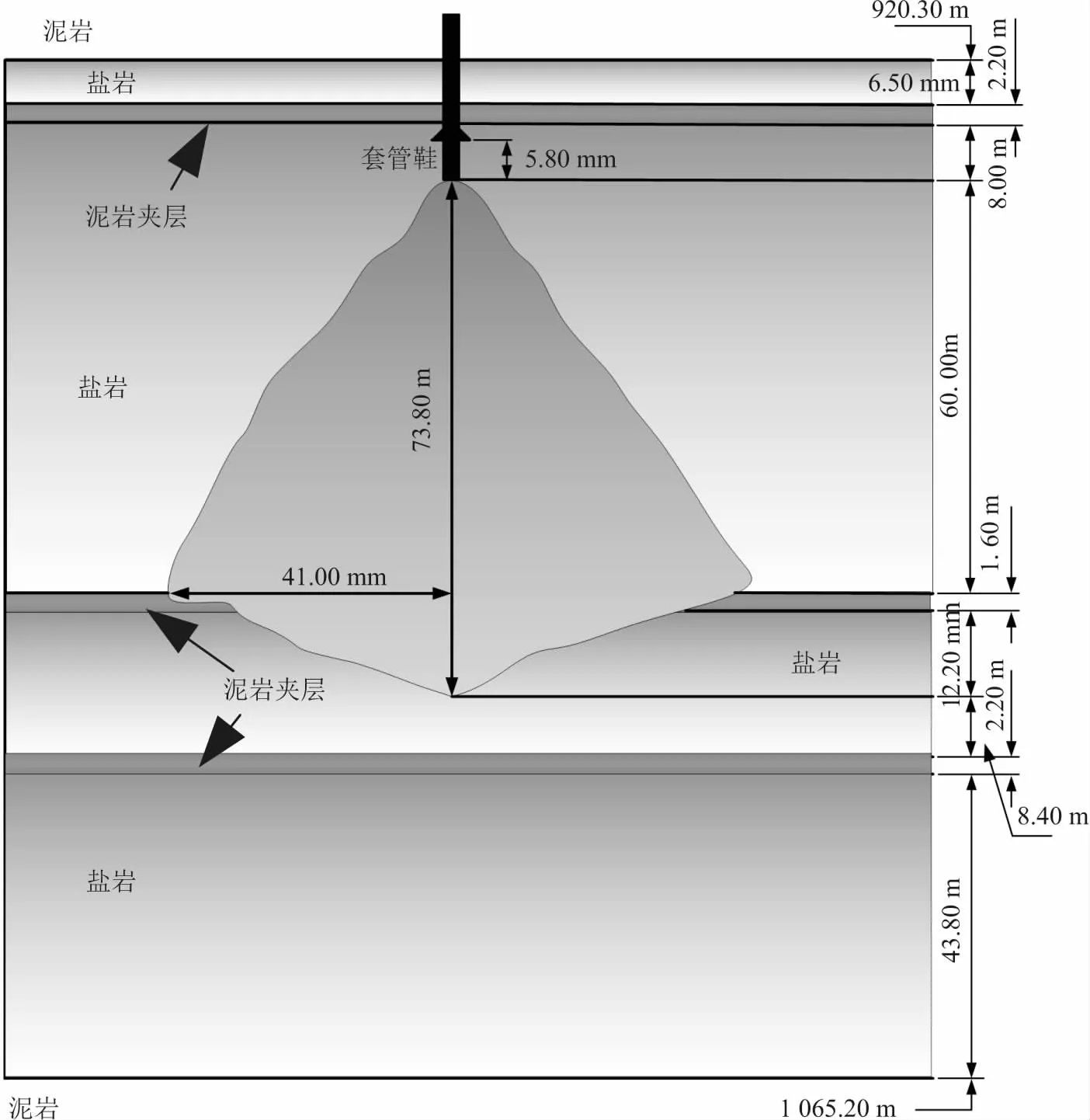
圖2 金壇某地下儲氣庫地層分布及剖面示意圖Fig.2 Stratigraphic distribution and vertical section diagram of an underground gas storage in Jintan

該地下儲氣庫腔體近似軸對稱，高度為73.80 m，腔體深度范圍為937.00～1 010.80 m，最大半徑為41.00 m，體積約為12.98×104m3，套管鞋位置為931.20 m，距離地下儲氣庫頂為5.80 m。基于相關資料，在充分研究地下儲氣庫安全性的內在特性、外界環境等要素的前提下，結合工程實際將該地下儲氣庫安全性評價指標歸納為3個集合共16個指標，見圖3。其中，運行參數間接地影響地下儲氣庫腔體的變化，不同的腔體和材質需要采取不同的運行指標，否則易造成失壓、失穩事故；腔體參數綜合表征了地下儲氣庫目前的安全狀態，通過不同的腔體指標反映地下儲氣庫不同角度的狀態是否安全；力學參數主要體現了地下儲氣庫巖體的性質，是從內在特性角度表現地下儲氣庫構成材質的安全狀態。

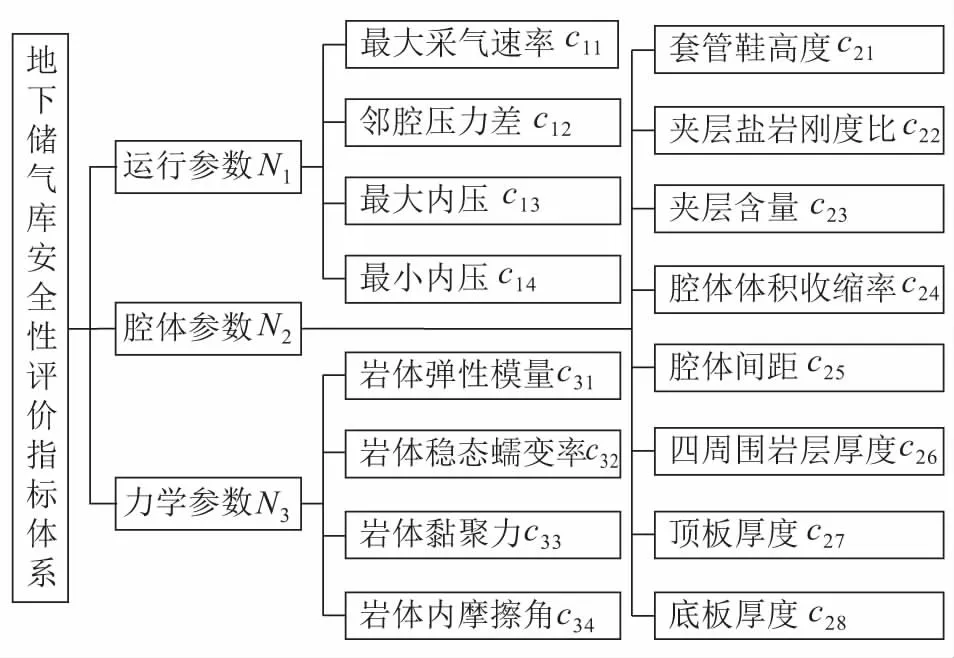
圖3 地下儲氣庫安全性評價指標體系Fig.3 Evaluation indexes system of underground gas storage security

為了便于分析，將部分指標進行了預處理：最大采氣速率、鄰腔壓力差、最大內壓、最小內壓分別用其實測值與模擬值的比值間接表示；腔體形狀用腔體體積收縮率間接表示；套管鞋高度用實際高度值與模擬值的比值間接表示；腔體間距、四周圍巖層厚度、頂板厚度和底板厚度分別用實際值與腔體直徑的比值間接表示。各指標實值和無量綱化數值，見表1。

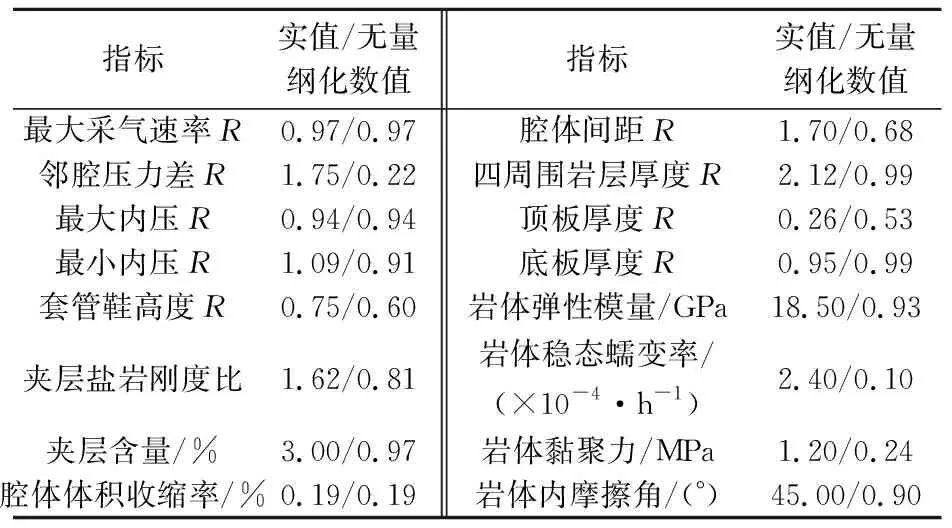
表1 某地下儲氣庫安全性評價指標值

定義安全性評判標準，根據心理學家Miller的研究結論：普通人對不同事物的區分數在5到9之間，同時參考已有相關研究的等級劃分[24-25]，將安全性設定為6個語意評價等級：1級為極不安全，2級為較不安全，3級為一般安全，4級為較安全，5級為很安全，6級為特別安全。該6個評價等級在語意上能夠有效區分，同時也能夠充分體現出安全性的不同狀態。根據武漢巖土力學研究所試驗評分模型[26]，可歸一化計算出地下儲氣庫安全性各指標相應的評價等級得分值區間，見表2。

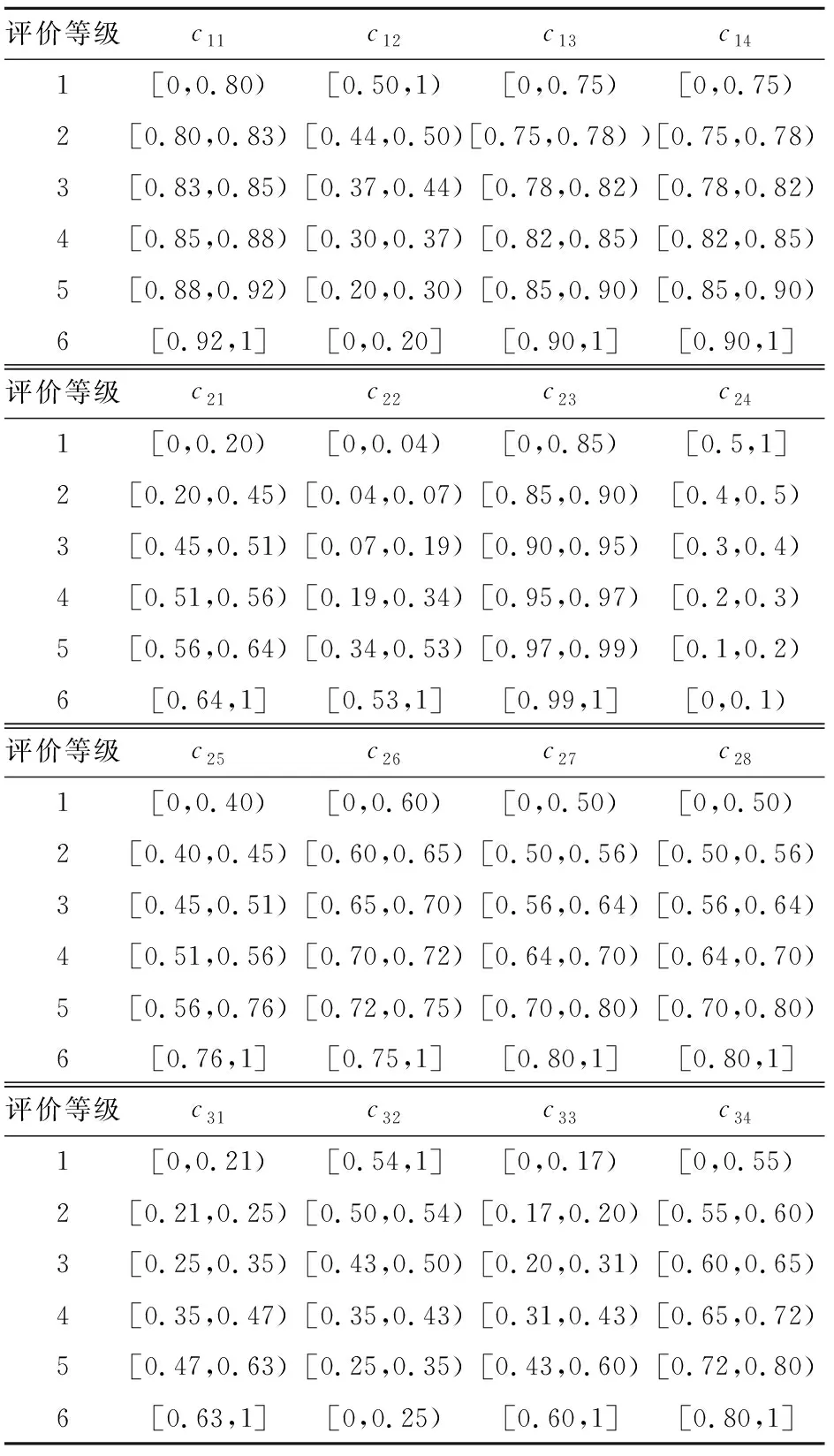
表2 地下儲氣庫安全性各指標相應的評價等級得分值區間

3. 1 確定經典域、節域和待評物元

將運行參數、腔體參數和力學參數分別作指標空間Ni(i=1,2,3)，則待評物元為

將安全性評價等級作為事物Qm(m=1,2,…,6)，以運行參數為例，其經典域如下：

其節域為

腔體參數和力學參數同理。

3. 2 計算單指標關聯度

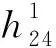
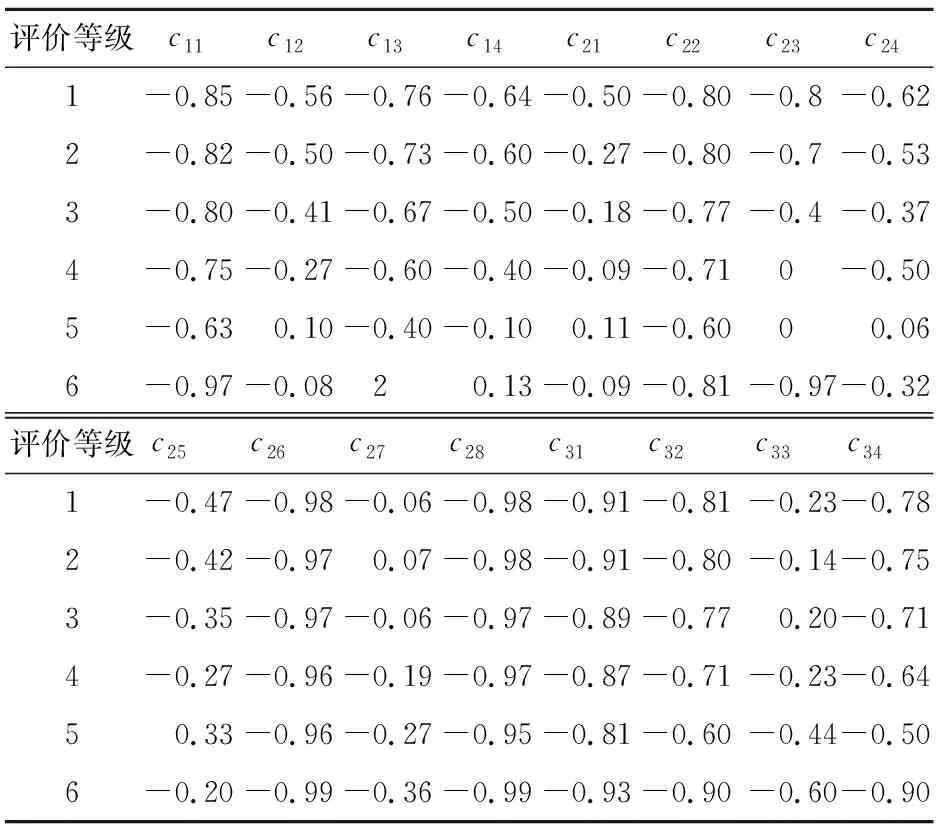
表3 某地下儲氣庫安全性各單指標關聯度的計算結果

3. 3 確定指標權重

首先，根據已確立的6個安全性評價等級標準，以直覺模糊值形式表示相應的定性語言變量如下：極不安全，[0.1,0.8]；較不安全，[0.2,0.7]；一般安全，[0.4,0.4]；較安全，[0.6,0.2]；很安全，[0.8,0.1]；特別安全，[0.9,0]。然后，邀請10名地下儲氣庫風險管理方面的專家針對安全性評價指標進行判斷，分別給出相應指標的直覺模糊評價信息，見表4。最后，計算各指標的權重，最終得到各指標權重的歸一化結果為：運營參數[0.072 3,0.024 9,0.067 0,0.070 5]；腔體參數[0.065 0,0.070 1,0.067 6,0.067 0,0.070 8,0.073 2,0.024 9,0.076 3]；力學參數[0.066 2,0.070 1,0.038 6,0.065 4]。

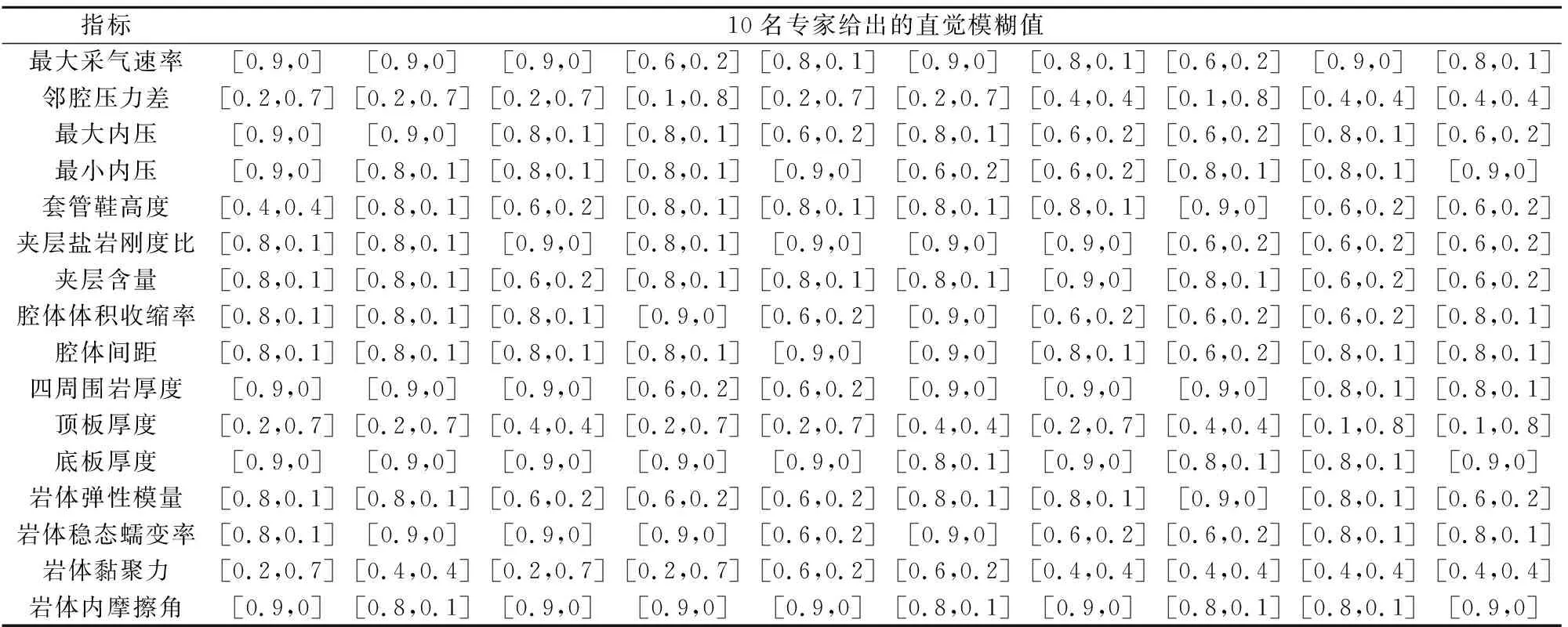
表4 某地下儲氣庫安全性評價指標的直覺模糊信息

3.4 計算多指標綜合關聯度并確定安全性級別變量特征值

將指標權重和單指標關聯度相乘，可得到各指標集相對于各安全性評價等級的綜合關聯度為：運行參數[-0.171 5,-0.163 0,-0.148 2,-0.129 4,-0.076 9,0.071 1]；腔體參數[-0.365 5,-0.330 2,-0.288 8,-0.257 2,-0.157 0,-0.320 7]；力學參數[-0.184 8,-0.178 3,-0.158 8,-0.164 6,-0.150 4,-0.215 8]。進一步可求得多指標綜合關聯度為：[-0.721 7,-0.671 5,-0.595 7,-0.551 2,-0.384 3,-0.465 4]。最終可求得該地下儲氣庫安全性級別變量特征值為4.663 3，根據已設定的安全性評判標準，以保守態度判定安全性等級，該地下儲氣庫安全性評價等級屬于第4級較安全狀態。

3. 5 評價結果分析

從評價結果可以看出，該地下儲氣庫安全性評價等級處于4級和5級之間，但是傾向于5級，即目前該地下儲氣庫處于較安全狀態，通過合理運營或者維修維護可以達到很安全狀態。對該地下儲氣庫安全性指標權重和各指標集與綜合評價級別進行分析，見圖4至圖6。

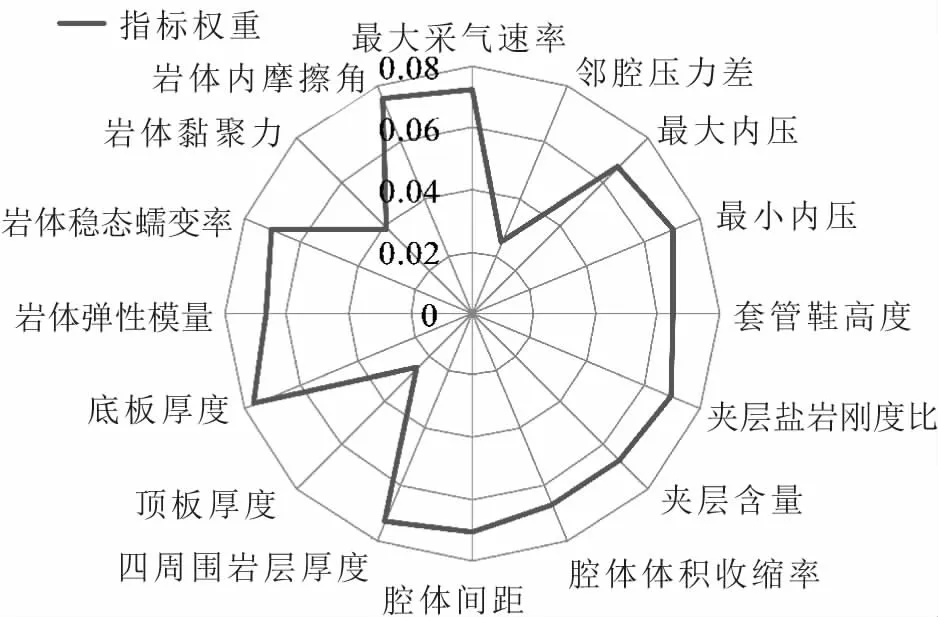
圖4 某地下儲氣庫安全性指標權重值雷達圖Fig.4 Radar chart of index weight values of a underground gas storage security

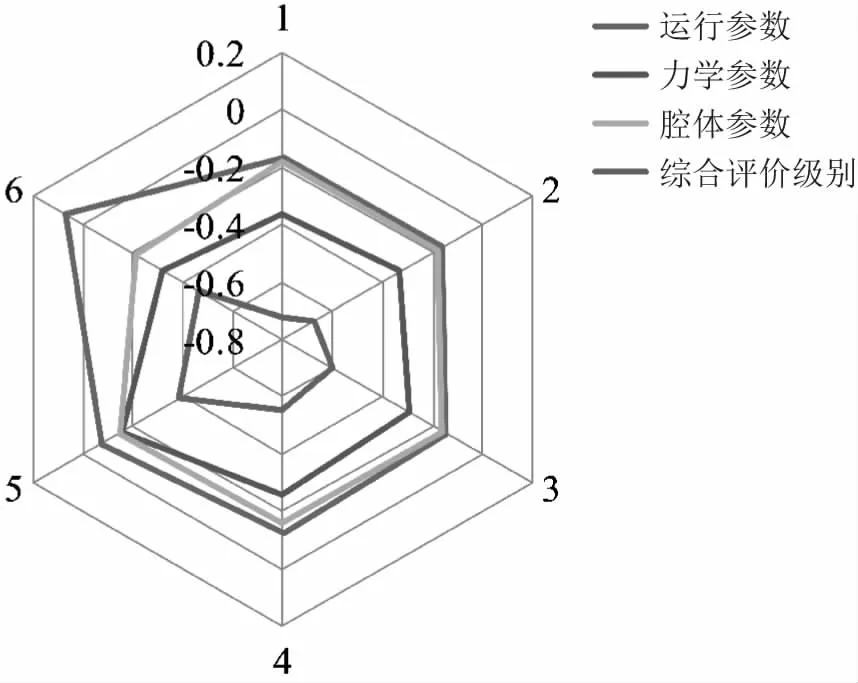
圖5 某地下儲氣庫安全性各指標集與綜合評價級別 雷達圖Fig.5 Radar chart of evaluation levels for compre- hensive security evaluation and index sets of an underground gas storage security

由圖4至圖6可知：該地下儲氣庫運行參數、腔體參數、力學參數的安全性水平分別為5.312 7級、4.318 6級和3.341級，說明參數中的指標具有缺陷，導致不安全性的存在(見圖5)；該地下儲氣庫的頂板厚度、四周圍巖層厚度和最大采氣速率指標的權重較高(見圖4)，在地下儲氣庫運營期需要重點監測，因為這些指標的改變會對地下儲氣庫安全運營造成重大的影響；通過對各指標具體分析得到目前處于5級很安全以下的指標有夾層含量(4級較安全)、四周圍巖層厚度(4級較安全)、頂板厚度(2級較不安全)和巖體黏聚力(3級一般安全)4項(見圖6)。

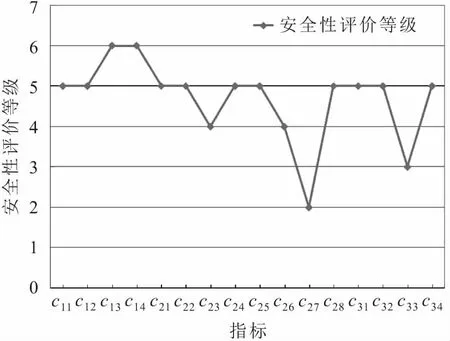
圖6 某地下儲氣庫安全性指標評價等級Fig.6 Index levels of an underground gas storage security

出現上述狀況的主要原因是該地下儲氣庫是由鹽礦改造而成，其中最大采氣速率、鄰腔壓力差等運行參數指標是可以進行修正的，通過運行參數的修正可從整體上進一步提高地下儲氣庫的安全性。其他缺陷指標因其固有屬性改善的難度較大，目前均符合相關安全規定，對該地下儲氣庫整體安全性的影響不大，屬于地下儲氣庫運營期可接受范圍之內，但是隨著地下儲氣庫運營時間的增加這些指標的風險性會增大，最終會引發整體失穩，故需要有針對性地對這些指標進行及時監測。

3. 6 敏感性分析

地下儲氣庫安全性評價指標的樣本信息比較稀缺，因此利用大量數據以統計分析的方式求取指標權重相對困難，故基于專家對指標的直覺模糊評價信息進行指標權重設計更符合實際情況，但由指標權重設計過程可知，不同專家因經驗、認知的不同會產生評審偏好差異，而偏好差異對評價結果的影響極大。本文假設表5中各指標的最優趨向、最劣趨向和最大統計趨向的直覺模糊評價信息為專家判斷結果，在該三種極端狀態下分別計算安全性級別變量特征值：最大統計趨向下的安全性級別變量特征值為3.834 1，一般安全；最優趨向下的安全性級別變量特征值為4.671 9，較安全；最劣趨向下的安全性級別變量特征值為2.374 4，較不安全。

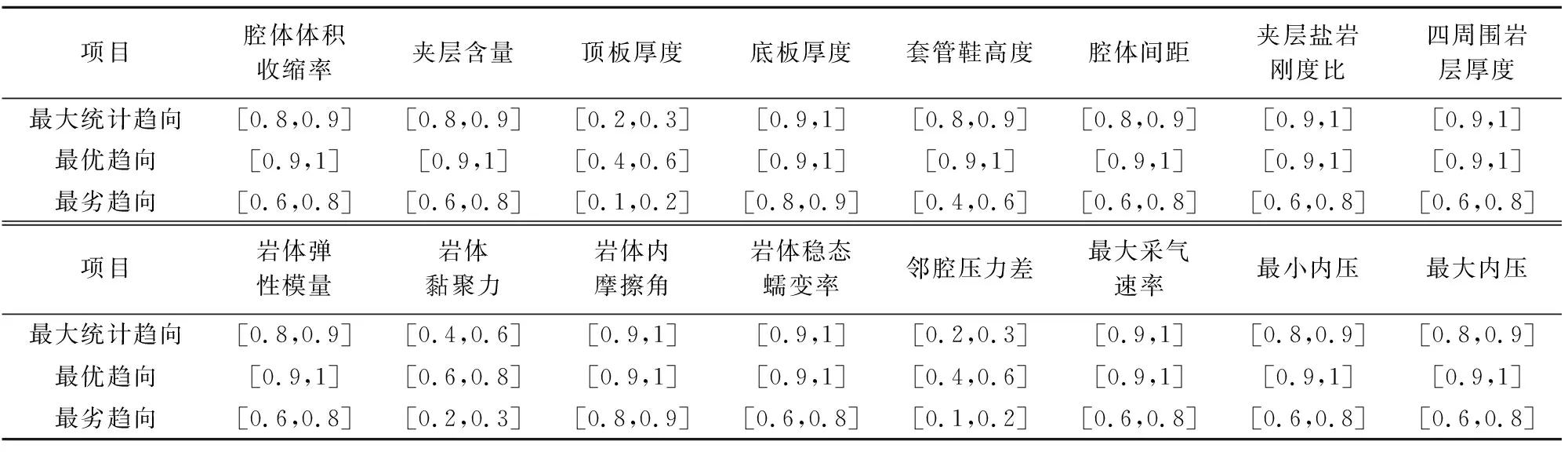
表5 專家直覺模糊偏好信息

由此可以看出，專家直覺模糊偏好信息的區別會導致最終評價結果的差異性：當所有專家對各指標的評價為相對最優時評價結果必然是樂觀的，反之評價結果是悲觀的；而最大統計趨向下得到的評價結果處于最優與最劣趨向評價結果之間，同時相對于實際評價結果趨于保守，原因是最大統計趨向的直覺模糊信息體現的是所有專家中最多的評審態度，而一般情況下專家在無法精確給出指標評價結果時通常選擇保守態度對待。因此，在對地下儲氣庫安全性進行實際評估時需要為各專家提供最優條件以達到精確判斷。

4 結 論

針對地下儲氣庫的安全性評價本文提出了一種基于直覺模糊信息和物元可拓法的評價方法。該方法應用直覺模糊信息進行指標權重計算，使用物元可拓法進行建模，并引入安全性級別變量特征值表達定量評價結果，最后通過江蘇金壇某地下儲氣庫的相關數據進行驗證，得到以下結論：

(1) 基于物元可拓理論構建的地下儲氣庫安全性可拓評價模型可以有效地解決評價過程中主觀定性判斷在定量化過程中難以轉化的問題。

(2) 應用直覺模糊信息進行安全性評價指標權重的計算，符合目前地下儲氣庫工程管理的實際狀況，能夠考慮專家偏好及不確定性信息，提高了指標權重的賦值精度和合理度。

(3) 地下儲氣庫安全性評價方法應用結果表明：評價模型不但可用于評判地下儲氣庫的安全性，還可以發現不安全的缺陷指標，從而有助于管理者有針對性的整改，可為油氣工程的安全評價提供新思路，有益于地下儲氣庫的長期安全運營和管理。