循環(huán)荷載作用下廣州軟土長期累積變形特性試驗研究

王 強

(中鐵十一局集團有限公司，湖北 武漢 430061)

軟黏土廣泛分布于我國的渤海灣、長江三角洲、珠江三角洲、長江沿岸以及江浙沿海等地區(qū)，因其具有強度低、蠕變性強、靈敏度高等特點[1-2]，受到工程界的廣泛關注，國內(nèi)外對軟黏土工程地質(zhì)性質(zhì)的研究也越來越多。軟土地區(qū)的地鐵振動誘發(fā)了一系列城市巖土工程問題，根據(jù)大量工程實踐資料反映，軟黏土地區(qū)的地鐵隧道在經(jīng)過一段時間的運營后，軟黏土地基將會產(chǎn)生較大的沉降。如林永國等[3]通過對上海地鐵一號線軟黏土地基的變形進行現(xiàn)場檢測，發(fā)現(xiàn)地鐵隧道縱向變形量過大，嚴重影響了地鐵的安全運營；蔣軍等[4]通過對長期循環(huán)荷載作用下黏土的一維沉降進行研究，發(fā)現(xiàn)我國京九線、京秦線等線路的粉土地基地段出現(xiàn)了不同程度的下沉松軟、翻漿冒泥、道渣陷槽等問題；Yasuhara等[5]研究發(fā)現(xiàn)，日本某低路堤高速公路在投入運營后，路基的5 a沉降量達到了1～2 m[5]。由此可見，長期的循環(huán)振動荷載對軟黏土地基沉降具有較大的影響。

目前國內(nèi)外眾多學者對軟黏土動力學特性進行了大量的研究，并取得了豐碩的成果。在國外，Matsui等[6]在0.02～0.5 Hz下對塑性指數(shù)為55的軟黏土進行了循環(huán)三軸試驗，發(fā)現(xiàn)軟黏土的孔隙水壓力和軸向應變隨循環(huán)振動次數(shù)的增加而增加，且荷載頻率越低，軟黏土的孔隙水壓力和軸向應變越大；Monismith等[7]通過對不同應力水平下軟黏土進行動力試驗研究，提出了表征軟黏土長期累積塑性變形與循環(huán)次數(shù)的指數(shù)模型；Li等[8]提出了修正的軟黏土長期累積變形計算的Power模型；Hyodo等[9]引入相對循環(huán)應力比的概念，提出了軟黏土殘余應變的計算模型；Stewart等[10]則建議用半對數(shù)方程來建立軟黏土長期累積塑性應變的計算模型。在國內(nèi)，朱登峰等[11]根據(jù)對上海淤泥質(zhì)黏土進行循環(huán)三軸試驗和不排水蠕變試驗的結果，分析了飽和軟黏土的孔隙水壓力、變形隨循環(huán)周數(shù)和應力幅值變化的增長規(guī)律；Ren等[2]提出了循環(huán)荷載下飽和軟黏土長期累積塑性應變的計算模型,該模型僅有3個參數(shù)，且物理意義明確、容易確定;黃茂松等[12]通過對上海地區(qū)典型飽和軟黏土進行不排水循環(huán)三軸試驗，分析了影響軟黏土累積塑性變形的主要因素，并研究了不同靜、循環(huán)動應力組合應力歷史影響下軟黏土的不排水循環(huán)長期累積變形特征。

由于形成環(huán)境的不同，軟黏土的形成過程也會有所不同，因此軟黏土具有明顯的區(qū)域性。目前我國學者對寧波[13-14]、上海[14-15]、天津[16]等地軟黏土的動力特性和變形方面的研究較多，而對廣州地區(qū)軟黏土的研究相對較少，僅有少數(shù)研究見諸報道，如匡月青等[17]對地鐵列車作用下廣州軟黏土進行了動力響應試驗研究，但是該研究未涉及到軟黏土的長期塑性累積變形方面。目前，針對地鐵、高鐵、公路等交通振動荷載作用下廣州軟土長期累積變形特性方面的認識不足，特別是針對廣州軟土變形隨循環(huán)荷載次數(shù)的變化規(guī)律和軟土長期變形預測模型方面的研究還不夠全面。

廣州市目前有多條地鐵線路穿越軟土地區(qū)，比如地鐵1號線、2號線、4號線、18號線等，因此研究循環(huán)荷載作用下廣州軟土長期累積變形特性和變形預測模型對該地區(qū)軟土地鐵隧道沉降變形控制至關重要。為此，本文以廣州南沙地區(qū)典型的軟土即淤泥質(zhì)黏土和淤泥質(zhì)粉質(zhì)黏土為研究對象，采用室內(nèi)GDS循環(huán)三軸試驗儀，考慮不同土體性質(zhì)和不同荷載頻率兩種影響因素,對廣州軟土進行了循環(huán)動三軸試驗，研究了循環(huán)荷載作用下廣州地鐵隧道附近軟黏土的長期累積塑性變形特性和規(guī)律。該研究成果可為廣州軟土地區(qū)地鐵隧道在長期振動荷載作用下軟黏土的變形控制提供依據(jù)。

1 循環(huán)動三軸試驗

1. 1 試驗土樣

試驗土樣取自廣州南沙區(qū)。南沙區(qū)位于廣州市沙灣水道以南，除十八羅漢山、黃山魯?shù)壬贁?shù)丘陵地貌外，基本全區(qū)覆蓋深厚軟土層[18]。南沙區(qū)軟土以海陸交互相軟土為主，其中與地鐵等人類工程密切相關的典型軟土是淤泥質(zhì)黏土和淤泥質(zhì)粉質(zhì)黏土。本次淤泥質(zhì)黏土取土深度為6.3～15.7 m，淤泥質(zhì)粉質(zhì)黏土取土深度為18.1～26.6 m，兩種試驗土樣的基本物理力學性質(zhì)指標，見表1。

表1 試驗土樣的基本物理力學性質(zhì)指標

1. 2 試驗儀器

本試驗采用英國進口的多功能動態(tài)循環(huán)三軸試驗系統(tǒng)，如圖1所示。該設備實時監(jiān)控整個試驗過程，高速采集并儲存試驗數(shù)據(jù)，是一套具有精度高、操作簡單、結果可靠等優(yōu)點的數(shù)字化試驗設備。

圖1 多功能動態(tài)循環(huán)三軸試驗系統(tǒng)Fig.1 Multifunctional dynamic cyclic triaxial test system

該試驗系統(tǒng)由加壓系統(tǒng)、量測系統(tǒng)和控制系統(tǒng)三部分組成。其中，加壓系統(tǒng)分別由3個控制器(反壓控制器、圍壓控制器和軸壓控制器)來實現(xiàn)，反壓控制器主要用來控制試樣中的孔隙水或空氣，并提供反壓飽和時的反壓力；圍壓控制器主要為壓力倉提供圍壓；軸壓控制器主要用來提供軸力并控制試樣的軸向變形(應變控制式和應力控制式試驗均通過該泵來實現(xiàn))。試樣的變形、壓力等數(shù)據(jù)通過傳感器傳至計算機處理控制系統(tǒng)。

1. 3 試驗方案

原狀飽和軟黏土在天然應力條件下，應力狀態(tài)處于K0固結應力條件。根據(jù)唐益群等[15]的研究成果可知，地鐵列車經(jīng)過時引起土體的響應頻率有兩個，高頻一般為2.4～2.6 Hz，低頻一般為0.4～0.6 Hz。因此，本次室內(nèi)試驗采用的兩個荷載頻率分別為0.5 Hz和2.5 Hz。

根據(jù)前人的研究結果[15]，列車及隧道體系施加給隧道底部的附加應力在20～40 kPa之間，故本次試驗采用的循環(huán)應力幅值為30 kPa。試驗的最大振動次數(shù)為5 000次，當試樣的應變在循環(huán)荷載次數(shù)100次以內(nèi)小于0.05%即可結束試驗。試驗方案及控制參數(shù)見表2。

表2 試驗方案及控制參數(shù)

2 試驗結果與分析

2. 1 土體性質(zhì)對土體循環(huán)累積變形特性的影響

圖2為典型循環(huán)荷載作用下土體軸向應變隨時間的變化曲線。在一次循環(huán)荷載中，土體應變可分為峰值、谷值和中值(中值為峰值和谷值的平均值)，為了便于分析，以下土體的累積塑性應變量均取中值。

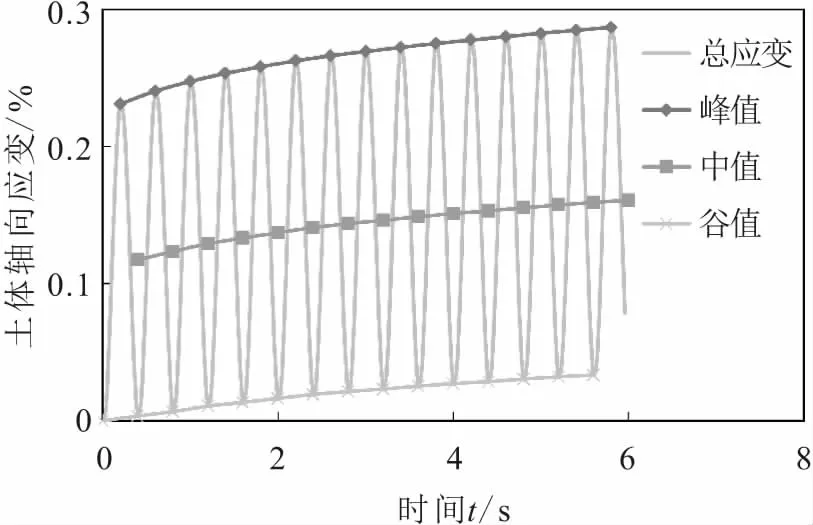
圖2 循環(huán)荷載作用下土體軸向應變的峰值、中值和谷值Fig.2 Peak，median and the valley values of soil axial strain under cyclic loads

圖3和圖4為在荷載頻率分別為2.5 Hz和0.5 Hz的循環(huán)荷載作用下淤泥質(zhì)黏土和淤泥質(zhì)粉質(zhì)黏土的循環(huán)累積變形曲線。

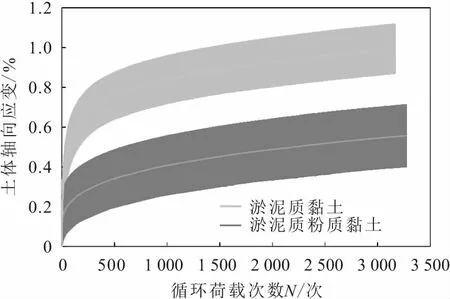
圖3 荷載頻率為2.5 Hz的循環(huán)荷載作用下廣州軟土的 循環(huán)累積變形曲線(中間曲線為土體應變中值線)Fig.3 Cyclic cumulative deformation curves of Guangzhou soft clay of soil under load frequency of 2.5 Hz (The middle yellow curve is the median strain line.)

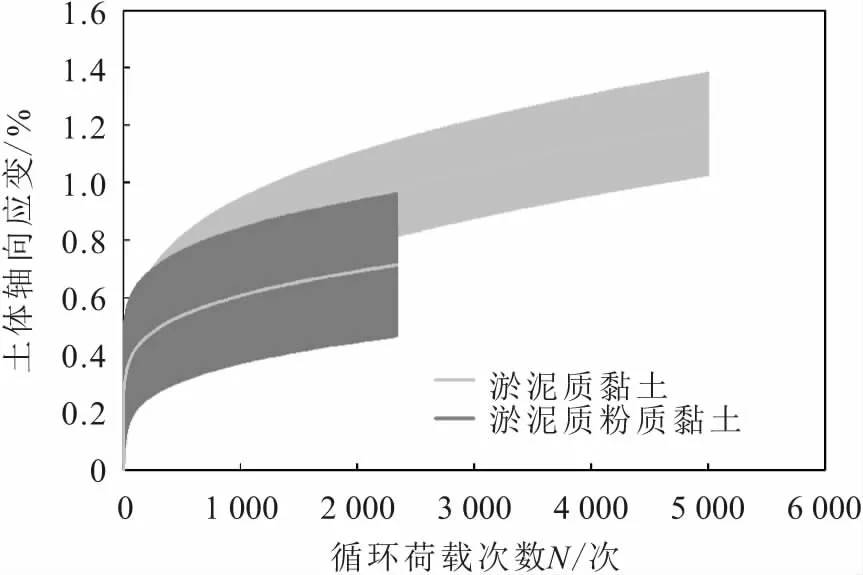
圖4 荷載頻率為0.5 Hz的循環(huán)荷載作用下廣州軟土的 循環(huán)累積變形曲線(中間曲線為應變中值線)Fig.4 Cyclic cumulative deformation curves of Guangzhou soft clay of soil under loads with frequency of 0.5 Hz (The middle yellow curve is the median strain line.)

由圖3和圖4可知：不論是在0.5 Hz還是在2.5 Hz的循環(huán)荷載作用下，淤泥質(zhì)黏土和粉質(zhì)黏土的循環(huán)累積變形曲線的變化趨勢基本一致，但兩種土體的累積塑性變形量明顯不同，淤泥質(zhì)黏土的累積塑性變形量明顯大于淤泥質(zhì)粉質(zhì)黏土，且前者的累積塑性變形量約為后者的1.6倍。

2. 2 荷載頻率對土體循環(huán)累積變形特性的影響

圖5為在荷載頻率為2.5 Hz和0.5 Hz的循環(huán)荷載作用下淤泥質(zhì)黏土的循環(huán)累積變形曲線。

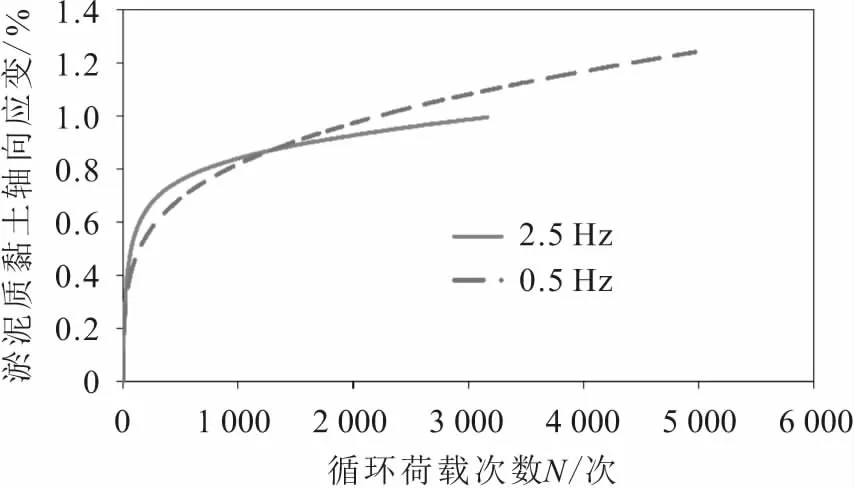
圖5 荷載頻率為2.5 Hz和0.5 Hz循環(huán)荷載作用下 淤泥質(zhì)黏土的循環(huán)累積變形曲線Fig.5 Cyclic cumulative deformation curves of silty clay under the cyclic loads with frequency of 2.5 Hz and 0.5 Hz

由圖5可知：以循環(huán)荷載次數(shù)N為1 500次為界限，1 500次之前2.5 Hz循環(huán)荷載作用下淤泥質(zhì)黏土的累積塑性變形量大于0.5 Hz循環(huán)荷載作用下的淤泥質(zhì)黏土，這是由于2.5 Hz循環(huán)荷載作用下的淤泥質(zhì)黏土的累積塑性變形速率(即土體累積塑性應變與循環(huán)荷載次數(shù)N的比值，單位為%/次)大于0.5 Hz下的淤泥質(zhì)黏土；1 500次以后2.5 Hz循環(huán)荷載作用下淤泥質(zhì)黏土的累積塑性變形速率逐漸小于0.5 Hz下的淤泥質(zhì)黏土，從而導致2.5 Hz循環(huán)荷載作用下的淤泥質(zhì)黏土的最終累積塑性變形量小于0.5 Hz下的淤泥質(zhì)黏土。

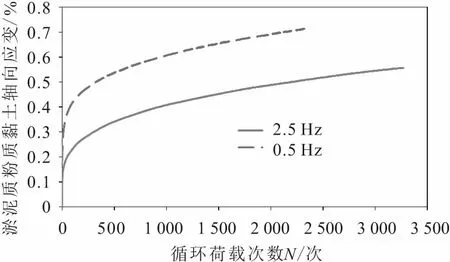
圖6 荷載頻率為2.5 Hz和0.5 Hz的循環(huán)荷載作用 下淤泥質(zhì)粉質(zhì)黏土的循環(huán)累積變形曲線Fig.6 Cyclic cumulative deformation curves of mucky silty clay under loads with frequency of 2.5 Hz and 0.5 Hz

圖6為在荷載頻率為2.5 Hz和0.5 Hz的循環(huán)荷載作用下淤泥質(zhì)粉質(zhì)黏土的循環(huán)累積變形曲線。

由圖6可知：在荷載頻率為0.5 Hz的循環(huán)荷載作用下的淤泥質(zhì)粉質(zhì)黏土的累積塑性變形速率和最終累積塑性變形量均明顯高于2.5 Hz循環(huán)荷載作用下的淤泥質(zhì)粉質(zhì)黏土。

圖7為荷載頻率對廣州軟土累積塑性變形速率的影響。

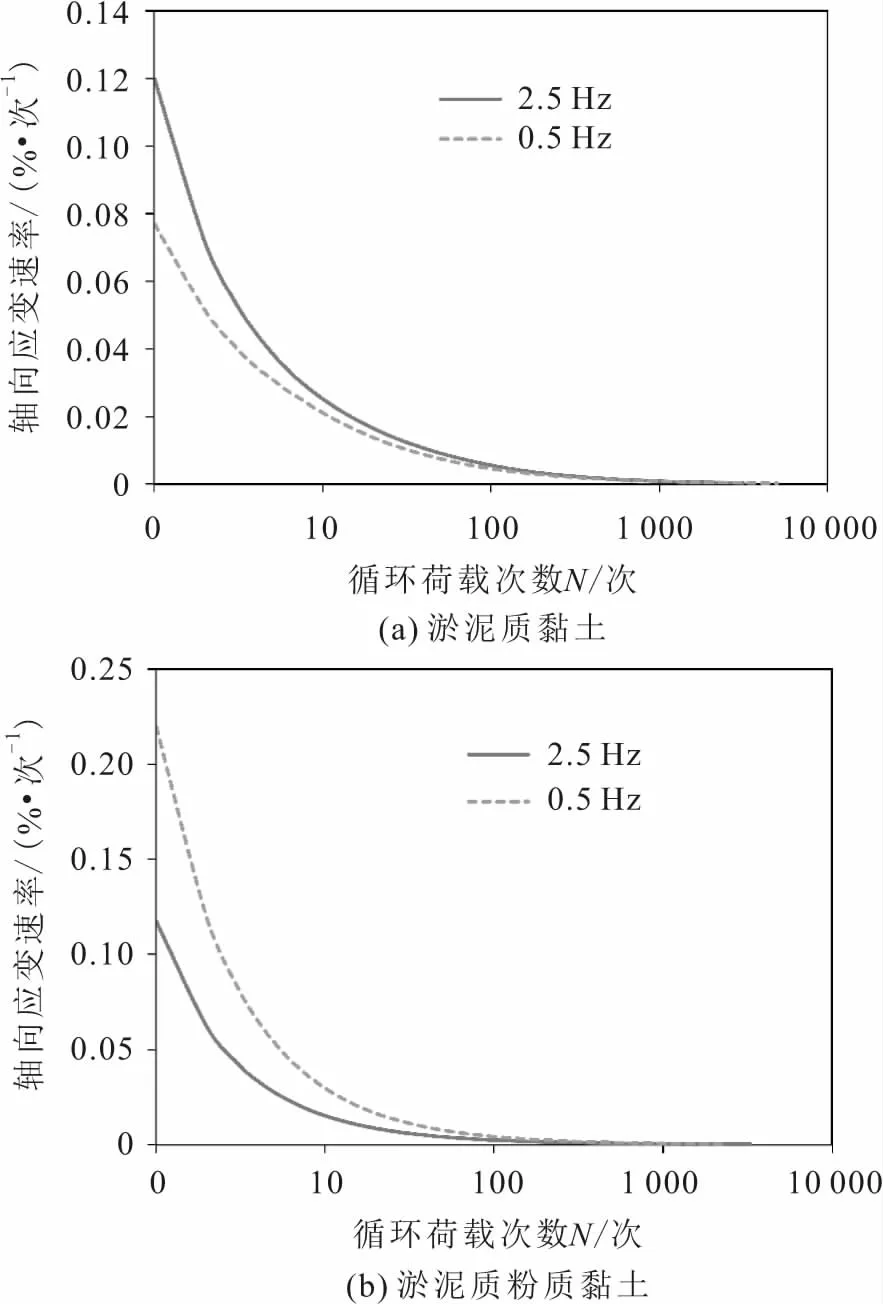
圖7 荷載頻率對廣州軟土累積塑性變形速率的影響Fig.7 Influence of frequency on accumulative plastic strain rate of Guangzhou soft clay

由圖7可見：荷載頻率對淤泥質(zhì)黏土和淤泥質(zhì)粉質(zhì)黏土累積塑性變形速率的影響具有明顯的不同，區(qū)別主要表現(xiàn)在循環(huán)荷載作用的前期(N<1 500次)，對于淤泥質(zhì)黏土，2.5 Hz循環(huán)荷載作用下的土體的累積塑性變形速率大于0.5 Hz下的土體，而淤泥質(zhì)粉質(zhì)黏土則相反。這可能是由于荷載頻率對軟黏土變形的影響與軟土的黏滯性、敏感程度和判斷標準有關，目前國內(nèi)外對此尚無定論。

2. 3 軟黏土的累積塑性應變計算模型

由前述可知，前人在考慮了多種因素對循環(huán)荷載作用下軟黏土累積塑性變形的影響下，已經(jīng)建立了許多軟黏土累積塑性應變的計算模型。然而，目前使用較為廣泛的是Monismith等[7]提出的經(jīng)典指數(shù)模型：

εp=α·Nb

(2)

式中:εp為土體的累積塑性應變(%)；N為循環(huán)荷載次數(shù)(次)；a、b為模型參數(shù)。

該模型主要考慮了循環(huán)荷載次數(shù)和土體特性對土體累積塑性應變的影響。

圖8給出了廣州軟土累積軸向應變模型計算值與實測值的對比曲線。

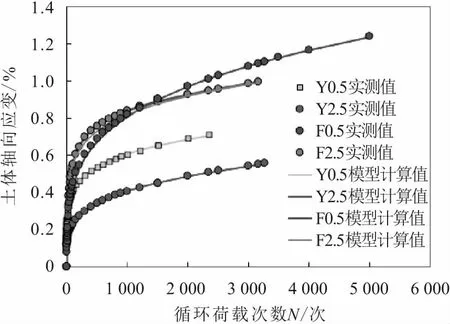
圖8 廣州軟土累積軸向應變模型計算值與實測值 的對比曲線Fig.8 Comparison of the accumulative axial strain model of Guangzhou soft clay between calculated results and measurements注：圖中Y0.5表示0.5 Hz循環(huán)荷載下淤泥質(zhì)黏土的軸向應變；F0.5表示0.5 Hz循環(huán)荷載作用下淤泥質(zhì)粉質(zhì)黏土的軸向應變。依此類推。

由圖8可知:模型擬合曲線與實測曲線完全吻合。可見，Monismith指數(shù)模型能夠滿足5 000次振動荷載作用下廣州軟土變形特性的描述和計算。

3 討 論

由于本試驗數(shù)據(jù)的缺乏，本文未考慮頻率、應力歷史、動偏應力等其他影響因素。本文根據(jù)Monismith指數(shù)模型所獲得的模型參數(shù)僅對廣州軟黏土在本試驗所設計的圍壓、反壓、荷載頻率、固結度、循環(huán)應力幅值等條件下才適用，不具有普遍適用性。

準確、合理的土體累積塑性應變計算模型是建立在正確的影響因素分析之上的，而影響土體動力變形特性的因素有很多，主要有土體的物理性質(zhì)(含水量、液限、塑限、密度、粒徑、顆粒比表面積等)、受力狀態(tài)(循環(huán)動應力水平、圍壓、超固結比、荷載頻率等)、應力路徑(加載荷載波形、加載方式、試驗控制方式等)等。在這些影響因素中，對于給定的土體，循環(huán)動應力水平和圍壓是決定土體長期累積變形最關鍵的因素。很多學者研究表明，土體存在臨界循環(huán)應力，當循環(huán)應力水平小于臨界循環(huán)應力時，無論循環(huán)荷載作用多長時間和多少次數(shù)，土體都不會發(fā)生破壞，即土體的累積塑性變形不會隨著循環(huán)荷載次數(shù)的增加而一直增大，而是趨于某一穩(wěn)定值；當循環(huán)應力水平大于臨界循環(huán)應力時，土體會在有限的循環(huán)荷載和次數(shù)內(nèi)發(fā)生破壞[1-2]。表3給出了不同黏性土的臨界循環(huán)應力值。通過本文的試驗結果可以發(fā)現(xiàn)，廣州地區(qū)淤泥質(zhì)黏土和淤泥質(zhì)粉質(zhì)黏土的臨界循環(huán)應力值應大于30 kPa。

由于高鐵、地鐵等行車荷載在地基軟土內(nèi)產(chǎn)生的動應力實際上往往低于其臨界循環(huán)應力值，因此行車荷載誘發(fā)的土體累積塑性變形在列車運營的初期會逐漸增大，但土體累積塑性變形速率逐漸減小到一定時間后土體累積塑性變形量達到最大并趨于穩(wěn)定，不再隨列車的運行而繼續(xù)增大。Monismith指數(shù)模型的土體累積塑性應變會隨著循環(huán)荷載次數(shù)的增加而持續(xù)增大，不能穩(wěn)定，因此該模型描述軟土長期累積變形可能是不恰當?shù)模⑶以撃Ｐ蛥?shù)是純粹的經(jīng)驗參數(shù)，且物理意義不明確，也不能通過容易獲得的土體物理力學參數(shù)而確定[2]。鑒于此，Ren等[2]在前人研究的基礎上，提出了循環(huán)荷載作用下飽和軟黏土累積塑性應變的雙曲線計算模型,該模型僅有3個參數(shù)，且物理意義明確、容易確定。該模型可表述如下：

(3)

式中:a、b、c分別表示土體初始應變、應變率、最終累積應變。

Ren等[2]也給出了該模型中a、b、c3個參數(shù)的計算公式和取值范圍，但a、c參數(shù)都與循環(huán)荷載動應力比(CSR)有關。

可見，對于廣州地區(qū)的淤泥質(zhì)黏土和淤泥質(zhì)粉質(zhì)黏土，Monismith指數(shù)模型可以描述中-短期循環(huán)荷載作用下土體的累積塑性變形，或者描述循環(huán)應力略大于臨界循環(huán)應力的土體累積塑性變形。而Ren模型適用于描述循環(huán)應力小于臨界循環(huán)應力的土體長期循環(huán)累積塑性變形(或者最終變形量)，可應用于廣州地鐵等行車荷載作用下軟土地基長期變形的控制與計算。

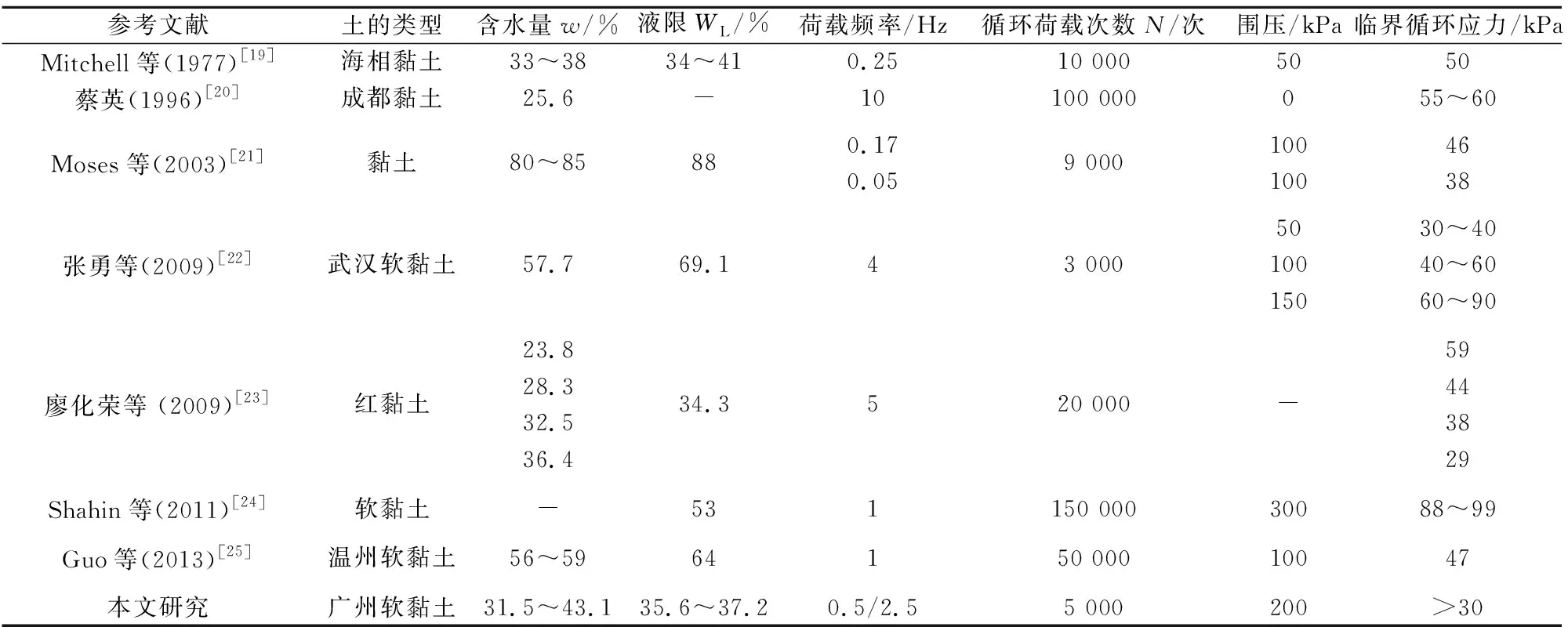
表3 不同黏性土的臨界循環(huán)應力值(根據(jù)Ren等[2]修改)

4 結論與建議

本文以廣州南沙區(qū)淤泥質(zhì)黏土和淤泥質(zhì)粉質(zhì)黏土為研究對象，通過室內(nèi)GDS循環(huán)三軸儀，在考慮土體性質(zhì)和荷載頻率兩種影響因素下對廣州軟黏土進行了循環(huán)動三軸試驗，研究了循環(huán)荷載作用下廣州軟黏土的累積塑性變形特性和規(guī)律，得到的主要結論如下：

(1) 土體類別和循環(huán)荷載頻率對土體變形均影響顯著。不論是在2.5 Hz還是在0.5 Hz的循環(huán)荷載作用下，淤泥質(zhì)黏土的最終變形量顯著大于淤泥質(zhì)粉質(zhì)黏土，且對于同一類土體，0.5 Hz循環(huán)荷載作用下土體的最終變形量大于2.5Hz下的土體。

(2) 在循環(huán)荷載應力幅值小于土體臨界循環(huán)應力時，廣州軟土的最終變形量隨時間(或循環(huán)荷載次數(shù))的增加而逐漸趨于穩(wěn)定。

(3) 廣州南沙區(qū)淤泥質(zhì)黏土和淤泥質(zhì)粉質(zhì)黏土的臨界循環(huán)應力值不小于30 kPa。

(4) 分析了現(xiàn)有常用的土體累積塑性應變計算模型的優(yōu)缺點和適用范圍，并推薦給出了適合廣州地鐵行車荷載作用下軟土地基長期變形控制與計算的模型。

需要指出的是，影響循環(huán)荷載作用下土體長期累積變形的因素很多，本文僅就土體類型(土的基本物性)和荷載頻率兩種因素進行了初步探索。今后擬對循環(huán)應力比、圍壓等重要影響因素展開研究。本研究成果是下一步工作的基礎，也可為廣州軟土地區(qū)地鐵隧道變形控制與計算提供依據(jù)。