雙減課堂：教學要在學生的困惑點展開

伍淵潑 （溫州市甌海區南白象新生小學，浙江 溫州 325000）

“雙減”政策實施以來，課堂和作業成為日常教研活動的兩大核心.尤其是課堂，它是我們實現減負提質的關鍵.因此，教師要轉變固有思維，改變用“提升作業量”彌補課堂上“營養不良”的方式.這就要求教師要深入解讀教材，研究學情，架設合理的學習支架，在課堂上幫助學生突破知識的重難點.但是部分教師習慣了照搬教材提供的課件上課，習慣了布置大量的作業以練代教，面對突如其來的提質要求，往往無從著手.對于小學數學這門學科，有什么行之有效的方法能夠幫助我們備出一節好課，實現減負提質呢？

中國唐代大文學家韓愈在《師說》中對教師職責的描述給了我們啟示.“師者，所以傳道授業解惑也”，其中“解惑”一詞道出了教師日常教學活動的核心任務，即教師不但要給學生傳授道理和知識，還要幫助學生解決困惑.這為課堂提質指明了方向，教學應立足于學生真實的學習困惑點，合理構建教學活動，幫助學生“解惑”.具體可以從以下三個方面入手.

一、突破再生經驗束縛產生的困惑點，讓學習更加深入

小學數學教學一個重要的任務就是幫助學生積累數學基本活動經驗，它也是培養學生數學素養的基礎.學生在第一次數學活動中獲得的經驗稱為原初經驗，通過對同類型問題的反復運用形成了再生經驗，此過程在于量的積累，學生能夠獨立完成.但是如果遇到本質相似但跨度較大的問題，之前形成的再生經驗往往會產生負遷移，阻礙最終基本活動經驗的內化.一般表現為：學生以為自己都會，但是結果卻是錯誤的.此時學生遇到的困難，產生的困惑（如圖1所示），正是教學展開的關鍵點.

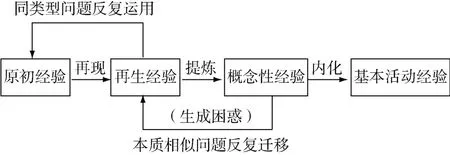
圖1 基本活動經驗形成路徑

如“植樹問題”一課.問：在一條長20 米的路一邊種樹，每隔5 米種一棵，可以種幾棵？學生在本課之前已經學習了除法，積累了大量的“包含”除的再生經驗.受此負遷移，學生自然用除法算式“20÷5＝4（棵）”解決.但通過畫圖驗證后，發現結果卻是5 棵.由此學生產生了第一個困惑點：為什么“包含除”失效了？同時，學生們第一反應就是對結果進行修正，補上算式4+1 ＝5（棵），但是為什么要加“1”，又讓學生十分困惑.這兩個困惑點正是我們展開教學的關鍵點.困惑的解決直指植樹問題模型的本質.此處我們只要把教學的重心放在討論算式20÷5 ＝4（？），4（？）+1（？）＝5（？）中4 處單位即可，尤其是辨清前一個4 和后一個4 的單位是否一樣.進而，引出一一對應的數學思想，完成“段”到“點”的轉化，從而突破學生的困惑.最后結合線段圖，讓學生明白“包含除”是在計算“段”數，而植樹問題是在計算段上的“點”數.由此學生對“包含除”運用的再生經驗完成二次迭代，對除法算式“包含除”意義的理解也更加深刻.

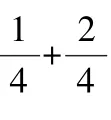
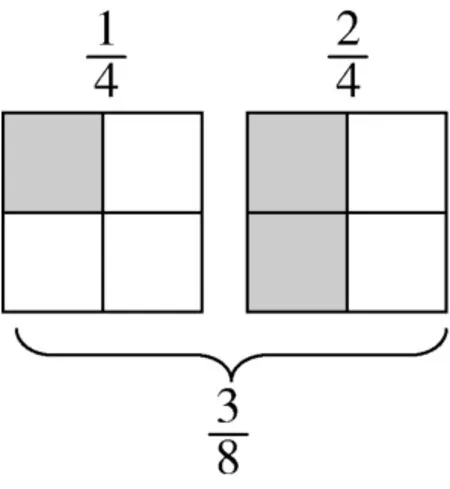
圖2 錯題示例

二、打通知識聯結障礙形成的困惑點，讓學習更加系統

數學是一門高度系統的學科，知識與知識之間存在相互關聯，它就像一張巨大的網絡，由局部的一條條知識鏈、一個個知識塊組成.因此我們在教學的過程中，要善于幫助學生打通知識之間的脈絡，讓知識點之間產生聯結，從而幫助學生形成系統性知識.由于年齡所限，小學生的知識建構能力相對薄弱，腦中的知識點多是點狀分部，且學生無法主動將它們建立聯結.因此這就需要教師以更加系統的方式進行教學設計，幫助學生突破困惑點.

如“四邊形的認識”一課.根據前測發現學生普遍認為：只有平行四邊形才是四邊形，長方形和正方形都不是四邊形.這正是由于學生認知圖形未建立聯系導致的.基于這樣的困惑，我們要從系統的角度出發設計這節課.首先，我們帶領學生畫出他們心目中的四邊形，在學生認可的例子中尋找四邊形的共性，從而用這樣的共性反過來去判斷長方形和正方形是不是符合.接著，我們為學生提供磁鐵小棒，去搭一搭“你認為最特別的四邊形”，并說說看“特別在哪里”.此時學生就會搭出長方形、正方形、各種普通的平行四邊形、各種梯形以及凹四邊形.借此我們可以順勢幫助學生理清四邊形、凹四邊形、凸四邊形以及各類四邊形之間的關系.打通四邊形整個體系的脈絡，為后續學習平行四邊形、梯形打下基礎.本節課的板書如圖3 所示，由圖可見整節課就是一條知識鏈，幫助學生串起四邊形的脈絡.

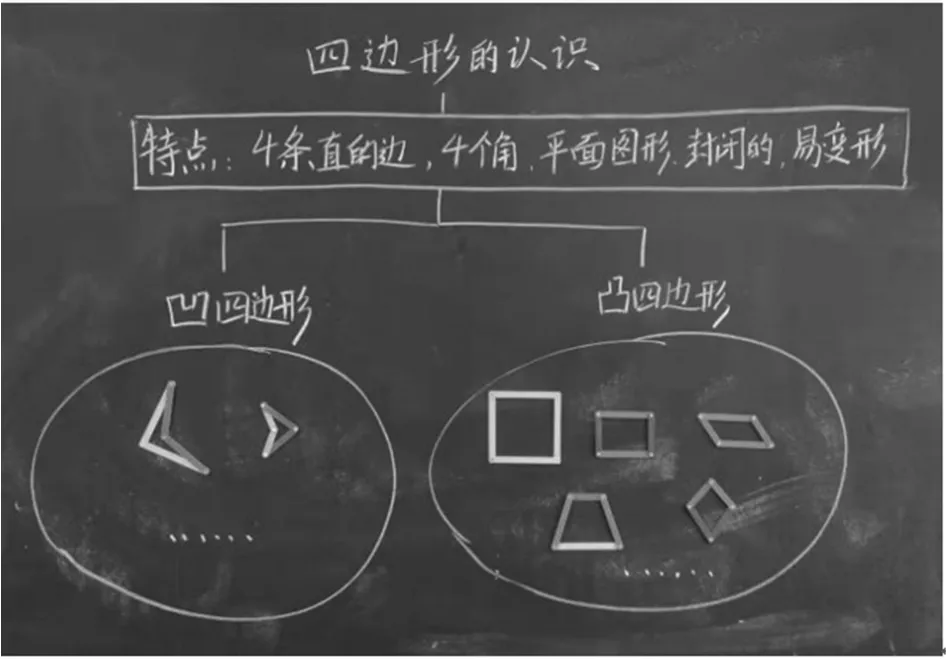
圖3 “四邊形的認識”板書

再如“小數的加減法”一課，學生在列小數加減法豎式的時候，受到整數加減法豎式寫法的負遷移，容易寫成末尾對齊.由此，學生普遍有這樣的困惑：為什么小數加減法要小數點對齊而不是末尾對齊？基于這種普遍的困惑，我們在教學完計算方法后，聚焦該知識點核心內涵，引入表1 中的教學環節，進行有效突破.表中共有4 條算式，教師引導學生對比觀察，發現這些算式都是在算2 個單位加5 個單位等于這樣的7 個單位，且都是相同數位上的數相加.將新知納入原有的認知結構中同化，幫助學生建立加減法知識鏈.此外，我們還可以引導學生在整數加減法的豎式上點上被“隱藏”的小數點，讓學生發現整數加減法末尾對齊其實就是小數點對齊，都是為了相同數位的數對齊，至此徹底打通整數和小數的加減法.這是整數和小數的縱向溝通，此外，在小數加減法的橫向知識鏈上，本節課還存在疑點.當我們給學生出示小數加減法學習的內容安排表時（如表2 所示），發現本節課之后小學階段不再學習三位、四位等多位小數的加減法.由此學生會產生第二個困惑點：為什么之后我們不再學習更多位數的小數加減法？接著教師只需要讓學生自己去挑戰更多位數的小數加減法，發現它們的算理沒有變，算法也相同.由此從橫向知識結構上幫助學生掌握了整個多位小數的加減法.

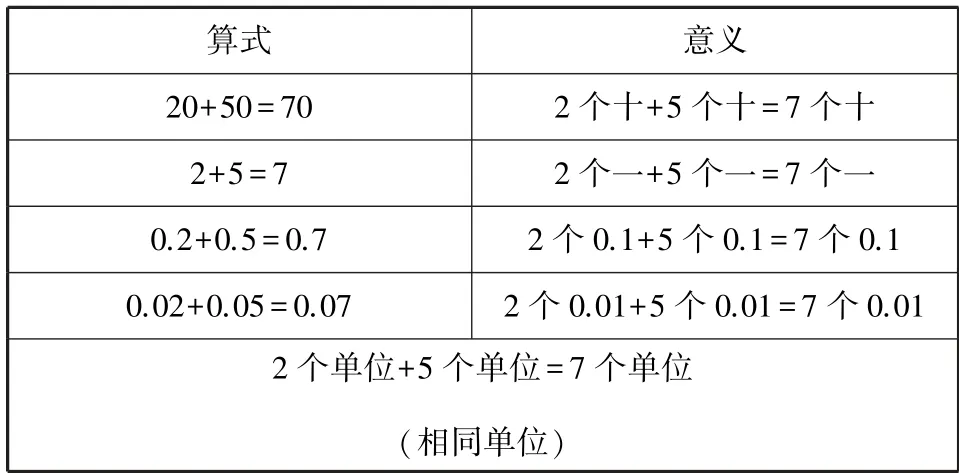
表1 整數、小數加法意義比較

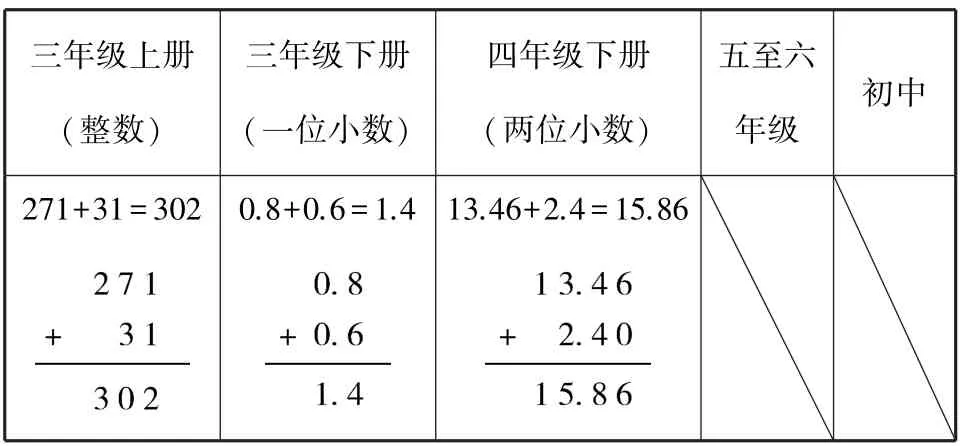
表2 各年級段小數加減法知識點安排表

三、充分利用困惑點制造思維碰撞，讓學習更加有趣

雙減背景下，我們都在努力提高課堂效率和質量，但是再精心設計的課程，如果學生沒有興趣參與其中，不積極主動地去學習，那也只能是教師的“一廂情愿”，教學依然無法有效開展.因此，提高學生學習的興趣至關重要.對此，許多教師做了相關的研究，例如有趣的教學情境、幽默的教學語言、多樣的教學手段等.這些研究大多從教學技藝的角度出發，在形式上尋求突破.實際上，數學教學中引人思辨的本質，是讓學生擁有挑戰的體驗，也是吸引學生投入學習的良方.有困惑的地方，必定會有爭議，思維就會有碰撞，數學學習的真實探究便得以生長.因此，我們要善于運用這些困惑點制造“碰撞”，讓學生全身心投入學習.反之，如果一節課沒有一處思維碰撞的地方，沒有一處值得大家為之爭一爭的“難點”，那么這節課要么是設計的難度太低，學生沒“吃飽”，要么是引導有問題，教師沒教好.

如“平行四邊形的面積”一課，學生的困惑點和爭議點主要集中在“平行四邊形的面積到底是鄰邊相乘還是底乘高”，這是由長方形面積公式學習而產生的負遷移.為此，教師要做的就是在課上將這個爭議點擴大，讓持有不同觀點的兩方學生說明理由，并讓其他學生選擇“站隊”.最終讓全體學生經歷猜想、驗證、歸納等過程，找到正確的計算方法.整節課，懂的學生希望說明白觀點，認真投入，不懂的學生因為打破了思維定式，印象更加深刻.

再比如“除數是兩位數的除法（試商）”一課，我們可以“人為”制造困惑點，激發學生進行思辨.課上，我們先引導學生計算：158÷52，97÷24，378÷63，從而得出四舍試商的算法.緊接著在PPT 上出示“96÷32 ＝”“325÷81 ＝”“247÷72＝”，讓學生口答試商.當學生滿心歡喜地認為自己掌握了方法的時候，順勢出示“158÷53 ＝”“95÷24 ＝”，讓學生先口答，再將試商過程寫下來.此時學生會發現，之前口答的“158÷53＝3”和“95÷24 ＝4”，試商都是錯誤的.為什么之前“158÷52＝3”“97÷24＝4”的四舍法試商是對的，而現在卻是錯的？利用產生的困惑激發學生的學習興趣，學生在對比辨析中發現了四舍法試商的局限性，調商的引入則水到渠成.有些學生在調商上進一步提出質疑：是不是有的情況調1 還不行，需要調2 呢？思辨的火花激發了學生濃厚的探索欲.

綜上所述，數學學習就是一個解惑的過程，數學課堂就是要在學生最困惑的地方發力，從而挖掘知識的深度，延展知識的廣度，成就高效、高質且富有趣味性的課堂.打破困惑的束縛，解放學生的思維，讓困惑之“繭”成為一種資源、一種力量，促使學生破繭重生、自我成長.