“線性代數”教學改革的思考與實踐
車國鳳,張麗麗
(廣東工業大學 數學與統計學院,廣東 廣州 510520)
一、教學改革背景
2020年12月,國務院總理李克強在主持國家科技領導小組會議上提出:“推動科技創新要引導各方面把更多注意力放在加強基礎研究、應用基礎研究上來……著力加強對數學等基礎學科發展的支持,夯實創新的基礎。”2021年7月,李克強總理再次強調要加強基礎研究,特別要重視數學,因為數學是一切學科的基礎。因此,數學學科越來越受到重視。“線性代數”作為大學數學中的一門重要基礎課,是中學數學相關知識的延續,其重要性不言而喻。與中學數學不同的是,其抽象性更強,邏輯性也更強。“線性代數”課程為土木、機械及自動化等幾乎所有工科專業的學習奠定堅實的基礎。
由于“線性代數”課程主要面向非數學類學生開設,且公式、定理等理論推導較多,所以學生學起來感覺比較吃力和枯燥。特別是近幾年,“線性代數”課程改革使得課時縮減,為了完成教學任務,一部分教師只能采取“滿堂灌”的教學方式,大大減少了教師與學生之間的互動,同時教學過程相對比較緊張。另外,隨著科學技術及網絡的發展,個別學生在課堂上走神的情形不僅是傳統課堂上的打瞌睡和聊天等,而更多的是低頭玩手機。盡管教師時常會走下講臺提醒學生,但這并不能從根本上解決問題。
二、教學改革措施
(一)使用混合式教學模式
混合式教學模式主要是指線上線下相結合的教學模式。近些年,隨著科學技術和信息網絡的發展,很多網絡教學資源可供借鑒,如中國大學慕課和SPOC等學習資源,而且大量的學習軟件可供選擇,如QQ、微信、騰訊會議及雨課堂等軟件。在“線性代數”教學中適當地結合一些網絡學習資源和學習軟件,可以很好地提高學生的學習效率。由于“線性代數”內容較多,且很多內容較抽象,學時較少,為使學生在有限的時間內很好地掌握教學內容,可以對線上線下學習內容做適當分類。需要指出的是,學習內容的分類非常重要,要在熟悉課程內容的基礎上,根據教學內容和學生學情進行恰當的分類,并在教學過程中根據學生的學習情況隨時做適當調整。經過初步的研討,在概念的引入、基本性質的介紹及簡單的計算等方面可以采取線上教學,如簡單的行列式計算、向量的概念介紹及其運算、特征值與特征向量的定義和性質、二次型的定義等內容;對于一些比較難理解的知識點,采用線下教學,如特殊行列式的計算、矩陣的乘法、矩陣的相似對角化等內容。以雨課堂教學工具為例,雨課堂學習對網絡速度要求較高,同時需要學生在手機上安裝微信,教師在電腦上安裝雨課堂軟件。在上課之前,教師任意打開一個PPT文檔,就會自動顯示出雨課堂,在雨課堂慕課視頻區域尋找合適的、時長適中的“線性代數”精品課程提前發送給學生預習,讓學生提前了解下節課將要學習的知識點及相關內容,而且可以使學生隨時隨地學習,不會厭煩,達到間接督促學生預習的效果。除此之外,雨課堂還有很多其他功能值得教師運用,例如,在課前,教師可以利用簽到功能快速地了解學生的出勤情況;在學習過程中,教師可以在雨課堂提前輸入一些題目,課堂上邀請學生作答,之后在雨課堂直接查看班級每個學生的作答情況,相比于傳統課堂提問個別學生的方式,這種線上的模式既省時間又可以提高教學效果;同時,學生可以隨時發彈幕表達自己的疑問,教師可以根據學生的問題大致掌握學生的學習情況,進而適當調整;在課程結束后,教師可以根據雨課堂中的數據,詳細地了解班級學生總體的學習情況及每個學生的學習狀況。
(二)將數學史融入課堂
由于“線性代數”比較側重于理論研究,內容相對枯燥,學生學習的積極性不高。為了提高學生的學習興趣,可以將與線性代數內容相關的名人軼事穿插課堂中。例如,引入早期運用矩陣概念數學家高斯的故事。高斯是一位非常著名的數學家,他在很小的時候就展現了極高的數學才華。在高斯發明自然數列求和公式之前,我們只能通過一個個數相加得出結果,運算量比較大,但是高斯在研究這個數列時,想出了一個快捷且準確的方法,這便是后來的自然數相加求和公式,這個公式為更一般的等差數列求和奠定了基礎,而且高斯想出此方法時僅有9歲。更為驚奇的是,在他只有3歲的時候,就可以看出他父親賬目中的錯誤并將其修改。高斯在1795年進入格丁根大學學習,當時對是否選擇數學專業也很不確定,鑒于他在數學上已經取得了一些成績,最后還是選擇了數學專業。事實證明,他的選擇是非常正確的。他在大學前兩年就在數學領域取得了很大的成就。特別是,他發明了二次互反律并解決了困擾數學家兩千多年的難題:只用圓規和直尺畫出正十七邊形。在1798年,高斯直接轉入黑爾姆施泰特大學,憑借他在數學上又取得的一個巨大突破:證明了代數基本定理,第二年直接博士畢業。高斯從上大學到博士畢業只用了四年的時間,足以看出他在數學學習上是多么出色。高斯從1807年開始就一直在格丁根大學工作,直到1855年去世。在高斯的一生中,他不僅在數學上取得了極高的成就,還在物理、天文等領域有很高的造詣。通過實踐可知,在課堂上融入一些數學家與數學歷史等故事,可以極大地提升學生學習“線性代數”的興趣,同時對學生數學素養的提高也起到了很好的效果。
(三)采用數形結合的方法
“線性代數”內容比較抽象,需要很強的理解能力才可以深刻理解其中的一些內容,對非數學類學生來說是一個比較大的挑戰。為了讓學生更深入地理解“線性代數”中的相關內容,教師采用各種各樣的方法,例如,采用實例法,將“線性代數”中的概念與已知的內容聯系起來,如在講解行列式概念的時候,先從二元一次線性方程組解的表達式講起,由其解的形式進而給出二階行列式的概念。在教學中發現,數形結合的方法在“線性代數”的學習中起到了很好的作用。通過圖表的形式把“線性代數”相關內容表示出來,既可以讓學生很清晰地理解其內容,又可以加深學生的印象。下面通過列舉一些例子,說明在“線性代數”學習中使用圖表的重要性。
1.在介紹行階梯型矩陣、行最簡形矩陣及標準形矩陣三者關系時,可以用圖1表示。從圖1中可以很清晰地看出,行階梯型矩陣包含行最簡形矩陣,行最簡形矩陣包含標準型矩陣。記住圖1就可以很準確記住上述三種矩陣之間的關系。
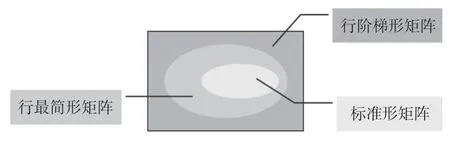
圖1 不同類型矩陣之間的包含關系
2.在介紹任意矩陣、行階梯型矩陣、行最簡形矩陣及標準形矩陣之間轉化關系時,可以通過圖2表示。由圖2可知,給定任何一個矩陣,都可以通過有限次初等行變換將其化為行階梯型矩陣,再經過有限次初等行變換化為行最簡形矩陣,最后可以經過有限次初等列變換,化為標準形矩陣,即任何矩陣可以經過有限次初等變換化為標準形矩陣,并且上述變換都是可逆的。
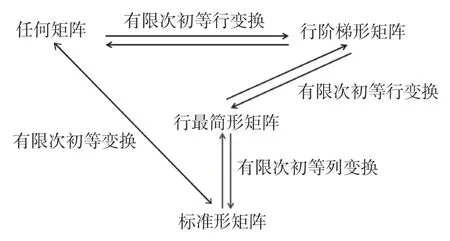
圖2 不同類型矩陣之間的轉化關系
3.在描述矩陣、向量組及線性方程組的解之間關系時,可以采用圖3表示。矩陣、線性方程組及向量組是不同章節的內容,學生學完之后不太容易厘清它們之間的關系,但通過圖3,可以很清晰地看到:(1)矩陣和線性方程組之間的關系可以通過線性方程組的系數矩陣連接;(2)矩陣和有限向量組的關系可以通過矩陣的行向量組或列向量組連接;(3)線性方程組與有限向量組之間的關系可以通過方程組的系數矩陣與常數向量之間的關系連接;(4)有限向量組與無限向量組之間的關系可以通過極大無關組連接。學生在了解矩陣、線性方程組及向量組關系時,只需要記住此圖形即可,既可以準確記住其主要知識點,又不容易混淆其內容。
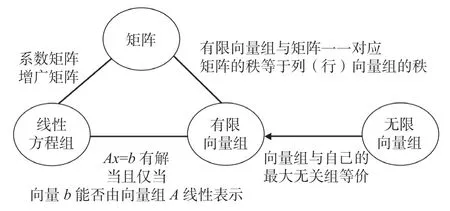
圖3 矩陣、線性方程組與向量組之間的關系
三、總結與建議
傳統的“線性代數”教學模式主要側重于教師在課堂上傳授教學內容,與學生溝通和交流比較少,很多時候教師不能準確有效地了解學生的學習效果。本文主要描述了筆者在教學過程中,為了提高教學效果所進行的一些改革舉措,主要體現在以下幾個方面:結合當下網絡資源,在“線性代數”教學中,根據教學內容和學生學情,把教學內容分類,然后將線上教學和線下教學相結合,以雨課堂和慕課為例,說明這種混合式教學模式效果良好;由于“線性代數”內容比較枯燥,筆者盡量將與教學內容相關的數學故事穿插課程教學中,極大地提高學生的學習興趣;由于“線性代數”中很多內容比較抽象,且課時相對較少而內容相對較多,為了讓學生更好地理解和記憶相關內容,在教學過程中通過圖形和表格的形式進行總結與概括。

