數學理解水平的劃分

李春雷于鳳來

數學理解水平的劃分

李春雷1，2，于鳳來3

（1．北京師范大學 教育學部，北京 100875；2．北京師范大學良鄉附屬中學，北京 102488；3．山東省莒縣閻莊街道中心初級中學，山東 日照 276535）

基于經典的數學理解內涵的闡釋以及已有各家理解水平的劃分，將學生數學理解劃分為工具性理解、關系性理解、創造性理解、文化性理解4個水平，并以均值不等式為典型案例，詳細解讀學生各數學理解水平的內涵和表現形態．工具性理解水平的價值不能忽視．學生個體數學理解水平是發展變化的，學生間的數學理解水平是有差異的．在力所能及的范圍內，鼓勵學生追根問底式地深層次學習，達到“關系理解”的水平；鼓勵學生對知識進行自我建構，達到“創造性”理解水平；鼓勵學生在歷史文化、審美情趣、人文關懷中進行熏陶，達到“文化性理解”的水平．

數學理解；工具性理解；關系性理解；創造性理解；文化性理解

信息時代知識記憶、數據計算的大部分功能可以由計算機代替，人的核心競爭力主要體現在對核心問題的理解力、創新力方面．理解是教育的永恒追求，數學理解是國際數學教育的重要研究主題．有效的數學教學需要認真致力于發展學生對數學的理解[1]．基于經典的數學理解內涵的闡釋以及已有各家理解水平的劃分，將學生數學理解劃分為工具性理解、關系性理解、創造性理解、文化性理解4個水平，以核心數學知識均值不等式為典型案例，解讀各數學理解水平的內涵．

1 數學理解的內涵

1971年，英國數學教育家、心理學家斯根普指出，理解某事意味著將它同化成適當的圖式，這說明理解具有主觀性[2]．新知識進入現有的認知結構或者促進認知結構的轉變，學習者才能理解知識．希爾伯特和卡彭特將數學理解看作是表征數學概念、數學事實的內部網絡的結果，如果數學的內部表征成為個人內部知識網絡的一部分，則數學被個人理解了；而如果數學知識和已有的網絡由更強或者更多的關系聯結著，則說明這個數學概念、數學事實或思想被人徹底地理解了[3]．1978年，格里諾認為，數學理解是一個過程，代表某種概念的關系結構能夠被理解[4]．1991年，皮瑞和基倫將數學理解當作一種整體的、動態的、層次的、非線性的、超驗回歸的、內在化的心理過程[5]．分析以上研究者對理解內涵的剖析可知，盡管有人認為理解是一種過程，有人認為理解是一種結果，但有著共同之處或相似之處，“圖示”“認知結構”“知識網絡”“關系”“聯結”“整體”成為了理解涵義的關鍵詞，都在于“認知結構”狀態的描述．

西蒙將教師當作數學理解的主體，認為數學理解是指教師根據學生的行為經驗建立一個連貫和具有潛在價值的組織，能將學生已有知識經驗轉變為學生的數學能力[6]．梅耶基于學生的視角，認為理解是學生創造性地利用呈現的信息去解決問題的能力[7]．數學理解的主體是教師還是學生，是教師對數學本體知識的理解，還是教師對學生數學理解的把握，或是學生對數學的理解？這個問題必須要搞清楚．數學理解水平的劃分關注的是學生數學理解水平的把握和判斷．

學生數學理解是指學生對數學本質的認識，知道數學概念、定理、公式、符號、思想方法、應用、創造的真實樣態，知道所學習的數學對象是什么、為什么、還能探究什么的一系列知識與技能．學生數學理解對象的核心是概念和關系．學生對數學概念的理解是指知道數學概念的定義、內涵（如概念的特征和性質）、外延（如分類與分類標準）、來源的真實樣態．學生對關系的理解是指知道數學定理、法則、公式及其推導過程，知道數量關系、圖形關系、隨機關系等數學研究對象之間相互關系的真實樣態．

2 數學理解的層次劃分

1976年，斯根普將理解分為工具性理解（instrumental understangding）和關系性理解（relational understanding）兩種模式[8]：前者是知道事物是什么，但不知為什么；后者是既知道事物是什么，也知道事物為何這樣，它揭示了數學知識的發生過程和邏輯規律，蘊含著一定的數學思想．1982年斯根普將數學理解又細分為工具性、關系性、邏輯性和符號性理解4種模式．

1978年，巴克斯頓將理解劃分為死記硬背（rote）、觀察（observational）、深刻理解（insightful）和邏輯理解（formal or logic understanding）4個水平[9]．

1982年，比格斯和科利斯描述的SOLO理論[10]，將學習者對某一個具體問題的反應水平分為前結構水平（prestructural）、單點結構水平（unistructural）、多點結構水平（multistructural）、關聯結構水平（relational）、拓展抽象水平（extended abstract）5個不同的層次[11]（見圖1）．其中單點結構、多點結構、關聯結構依次表示學習者只知道一個相關方面、知道幾個相關方面、知道將幾個相關方面形成一個整體的結構；最高理解水平為拓展抽象，代表學習者能夠調用頭腦或題目中的多個認知素材，得到的結論或觀點具有高度概括性、抽象性、衍生性、新穎性．

圖1 SOLO分類理論的5種水平

1987年，格里諾和賴利將數學原理劃分為3個逐漸復雜的理解水平：可以依據原則解決問題但缺乏對原則認識的“遵從水平”，可以完成性能評估判斷性任務和應用問題但只可意會不可言傳的“隱性理解水平”，能夠口頭陳述知識原則和程序結果的“顯性理解水平”[12]．

1988年，皮瑞—基倫建立的“超回歸”數學理解模型[13]（圖2），將數學理解分為8個水平，分別為初步了解（primitive knowing）、產生表象（image making）、形成表象（image having）、關注性質（property noticing）、形式化（formalizing）、觀察評述（observing）、組織結構（structuring）和發明創造（inventing）．將“發明創造”作為理解的最高層次，用返回原處揭示數學理解的非單向性．

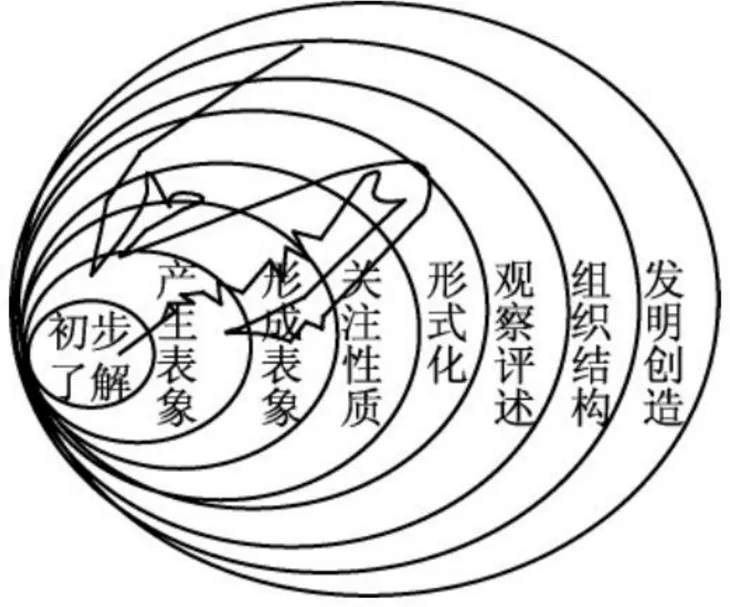
圖2 皮瑞—基倫理解模型

1998年，威金斯和麥克泰格指出，理解包括解釋（explanation）、釋義（interpretation）、運用（application）、洞察（perspective）、移情（empathy）和自知（self-knowledge）6個維度[14]．這種分類綜合了個體所展現的認知理解、學習的遷移以及情感共鳴．

2006年，索耶強調了概念理解的重要性，指出在今天的知識經濟時代，僅記憶事實性知識和程序性知識遠遠不夠，重要的是能對復雜概念形成深刻的概念性理解，并能基于這些理解生成新的觀點、新的理論、新的產品和新的知識[15]．

2012年，扎爾曼·尤西斯金在第12屆國際數學教育大會（ICME12）上，發表了題為“什么是對數學的理解？”的研究報告，將數學理解劃分為算法技能、性質證明、應用情境、隱喻表征、歷史文化共5個維度[16]．

2009年，鞏子坤構建了包括直觀理解、程序理解、抽象理解、形式理解的數學理解模型，認為形式理解是基于邏輯推理，來證實運算結果的合理性[17]．2012年，徐彥輝認為數學理解包括記憶性、解釋性、探究性3種方式[18]．2013年，匡金龍等將數學理解劃分為經驗性、形式化、結構化、文化性共4個理解層級[19]．2014年，王瑞霖等確立的數學理解層次結構的理論模型，包括表象理解、解釋理解、建立聯系、思想運用和創造生成5個層次[20]．2018年，谷曉沛等將函數概念的理解水平確定為感知水平、釋義水平、關聯水平、抽象水平[21]．

從以上學者對數學理解的分析來看，數學理解水平是有層次之分或階段之分的，但分類標準的不同，語義內涵的不同，導致分類結果的不同，也導致對學習者數學理解水平評價時，仁者見仁，智者見智．應借鑒整合已有研究成果，尋找數學理解層級的字面語義與內涵能夠較好統一、主體層級少而精、層級鑒別方法比較清晰的分類方法．

斯根普早期將數學理解分為“工具性理解”和“關系性理解”兩種模式；皮瑞—基倫建立的“超回歸”數學理解模型中的最高層級為“發明創造”，不妨將其稱為“創造性理解”；匡金龍等將數學理解的最高層級認定為“文化性理解”．將數學理解劃分為“工具性理解”“關系性理解”“創造性理解”“文化性理解”，能否較好統攝以上各家的分類方法？分析見表1．

2.1 “工具性理解”的統攝性

“工具”，人們能夠識別它，對外懂得它有什么用途，知道怎樣用，記住操作步驟就可以了，而不太關心它的內部構造．斯根普認為“工具性理解”是知道事物是什么，但不知為什么，將“工具”一詞運用到“數學理解”的最低層次，語義上也達到了生產“工具”與數學問題解決“工具”內在意蘊的吻合．學者們所劃分的“死記硬背”“觀察”“單點結構”“遵從”“隱性理解”“初步了解”“產生表象”“形成表象”“關注性質”“記憶事實性知識和程序性知識”“算法技能”“符號性””“直觀理解、程序理解”“記憶性”“經驗性理解”“表象理解”“感知”水平，都能被較好地統攝到“工具性理解”水平．

2.2 “關系性理解”的統攝性

“關系”，代表至少兩個事物之間具有的聯系，而不是事物孤立的存在．斯根普認為“關系性理解”既知道事物是什么，也知道事物為何這樣．斯根普后來細分的“邏輯性”水平和其他學者劃分的“深刻理解”“邏輯理解”“多點結構”“顯性理解”“形式化”“觀察評述”“結構化”“解釋”“釋義”“性質證明”“組織結構理解”“建立聯系”“思想運用”水平，都能被較好地統攝到“關系性理解”水平．

2.3 “創造性理解”的統攝性

創造性、創新性反映了從無到有、從有到新的過程．學者們劃分的“關聯結構”“拓展抽象”“發明創造”“運用”“洞察”“自知”“生成新的觀點、新的理論、新的產品和新的知識”“應用情境”“隱喻表征”“抽象理解”“探究性”“創造生成”“關聯”水平，都能被較好地統攝到“創造性理解”水平，代表學習者發現了數學對象間的不易被察覺到的關系，建立了研究對象的遠距離聯系，能將所獲得的數學結論進一步推廣到更大領域，面對種種不確定性和非連貫性能夠自發地創造．

2.4 “文化性理解”的統攝性

數學不僅蘊藏著強大的理性精神，也彰顯著巨大的人文情懷．扎爾曼·尤西斯金劃分的最后一個維度“歷史文化”水平，威金斯和麥克泰格劃分的“移情”水平，都能被較好地統攝到“文化性理解”水平．移情是指一種能深入體會他人的情感和觀點的能力，促使學習者能夠從多個角度思考問題，開闊胸襟．

綜上所述，“工具性理解”注重的是數學結論的事實性及其簡單應用性，“關系性理解”注重的是數學知識獲得的過程性及其結構性，“創造性理解”注重的是數學知識的關聯性及其擴展性，“文化性理解”注重的是數學發展的歷史性和人文性．因而可將學生“數學理解”的水平從時空上劃分為“工具性理解”“關系性理解”“創造性理解”“文化性理解”4個水平．前3者是從空間維度闡釋數學理解的由淺到深、逐漸復雜的層次水平，最后者是從時間維度、歷史角度、精神層面、審美情趣視角闡釋數學理解的層次水平．

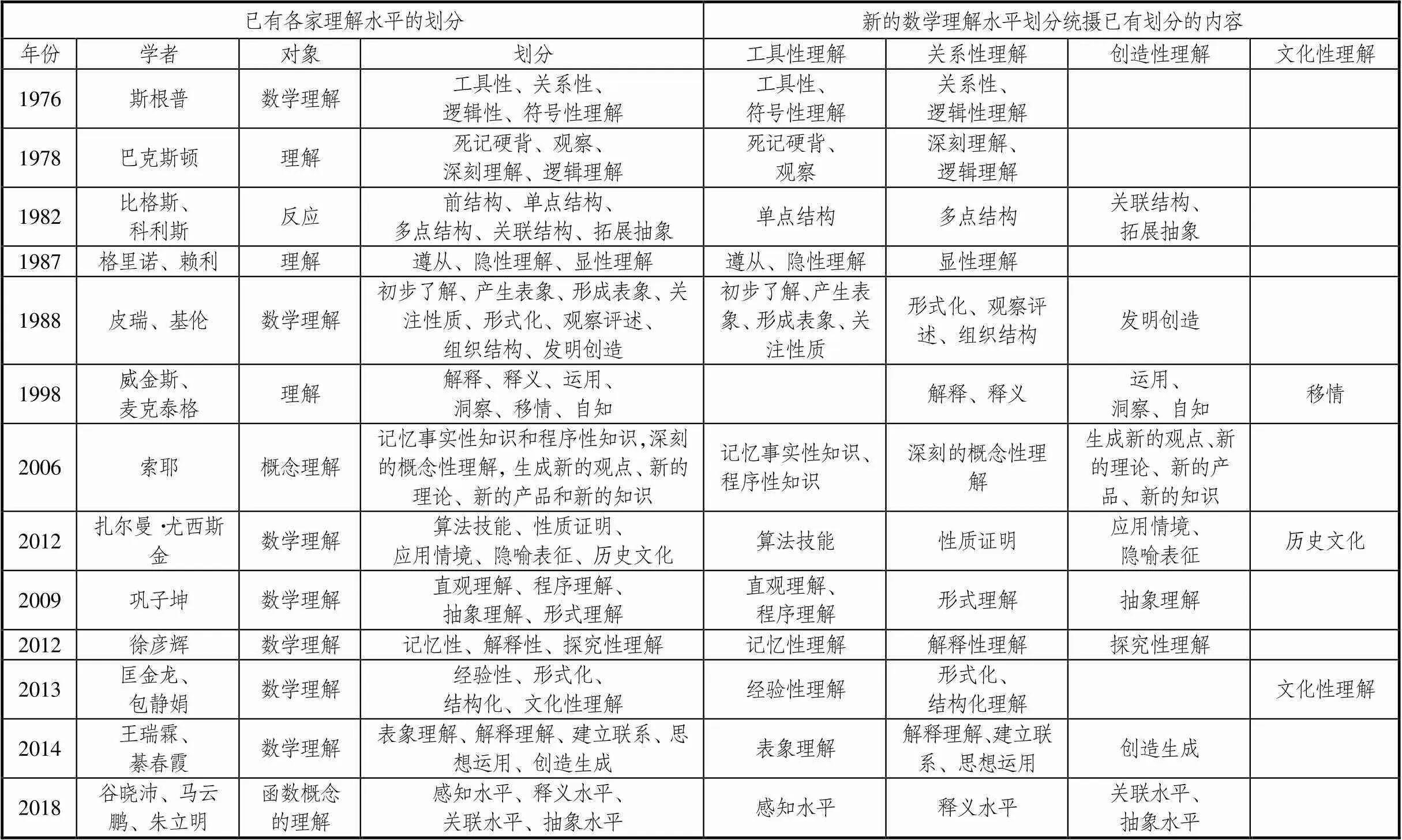
表1 新的數學理解水平劃分對已有觀點的統攝對照

3 案例解讀學生數學理解水平的層次劃分

3.1 工具性理解水平

工具性理解表現為“知其然，不知其所以然”．工具性理解水平的學生，知道符號所指代事物的意義，或是一種程序性的關于規則如何操作．工具性理解涉及的知識較少，短期內有作用，但長期內作用有限；需要記住數學知識，加重了記憶負擔．工具性理解水平有以下表現形態．

理解事實性知識是什么．學生知曉數學研究對象的定義和規律，即對數學概念、理論、思想以及觀點等了解，但未能完全認識，乃是一種機械記憶．如學生知道兩個正數的算術平均值、幾何平均值的概念，知道均值不等式的文字表征：“兩個正實數的算術平均值大于或等于它們的幾何平均值．”

理解知識屬性是什么．學生在已有認知的基礎上，基于數學活動經驗，能梳理、歸納、概括事物的某些特征與規律，知道一些屬性，能夠描述其意義，具有鮮明的個性化特征．如學生知道均值不等式是一個絕對不等式．

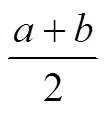
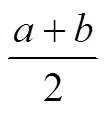
理解知識的功能是什么．學生能夠說明其作用，簡單初步使用該對象的某些性質，解決一些封閉性數學問題．如學生見到問題：“對于均值不等式，它有什么用？你想一想可以研究哪些問題？”能夠回答出均值不等式可應用于大小的比較、求函數的最值以及值域、求解參數的取值范圍等．

理解操作程序是什么．學生將問題解決算法化，能夠按規則運算，依照固定的模式獲得正確答案．精確的計算和對各種題型的熟練把握似乎成為數學學習的主旋律，對問題的反應常常停留在死記硬背操作步驟的層次，不明白為什么要采取這樣的順序．如學生知道均值不等式求最值的程序為“一正二定三相等”，并且能夠熟練操作，但是不清楚順序調整將會出現哪些問題．

3.2 關系性理解水平

關系性理解表現為“不僅知其然，還知其所以然”．關系性理解水平的學生，能夠對數學定理、原理、規則進行邏輯分析或證明，將數學知識的形成和論證提升為數學思想方法層面，與周圍知識進行邏輯聯結，將知道的一系列的數學事實構建成知識體系和模型，關系圖式是一種高質量的關系組織形式．關系性理解減少了記憶負擔，過濾了頭腦中無效的信息，適應新任務的能力更強，記憶更長久．關系性理解水平有以下表現形態．

理解證明的過程．學生知道為何一個數學陳述是正確的或者某個數學規則來自哪里，能夠邏輯證明數學結論的嚴密性、正確性．例如對于問題：“想一想均值不等式可以用哪些方法證明？”學生能夠給出均值不等式的綜合法、比較法、反證法、分析法等證明方法，表明理解了這一不等式成立的根據．

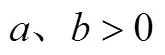
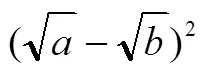
理解數學結構的深化與發展．學生知道新觀念能夠與哪些已有結構可以融合，將事物按照最簡潔、最規則、最協調、最具聯系的方式進行組織．從宏觀上來看，結構是各要素之間協調與綜合關系的組成模式；從微觀來看，結構表現為知識間的聯系與層次遞進；從發展觀來看，學生的思維結構和心理結構是不斷深化的．如在均值不等式的學習中，學生知道在概念結構系統中，增添了3個新成員，即算術平均值、幾何平均值、均值不等式；在運算結構系統中，算術平均值是加、除的運算結果，幾何平均值是乘積、開方的運算結果；在數列結構系統中，算術平均值、幾何平均值分別是兩個正數的等差中項、正的等比中項；在大小的順序結構系統中，不等號體現算術平均值、幾何平均值內在必然的大小關系；在等價結構系統中，“當且僅當”條件就是一種等價關系，“大于或等于”又可以等價表征為“不小于”；在數學思想結構系統中，化歸思想、解方程思想、等價轉化思想、數形結合思想對于均值不等式的研究至關重要；在數學工具結構系統中，比較兩個數或式的大小、求函數的最值或值域問題，又增添了一個工具“均值不等式法”；在不等式結構系統中，均值不等式是絕對不等式，而不是解不等式等．

3.3 創造性理解水平

創造性理解表現為“不僅知其然、知其所以然，還能知新的‘然’‘所以然’”．創造性理解水平的學生，能夠將數學觀念運用于變式狀態下的數學情境，發現數學對象之間的遠距離關聯，提出新問題，進行新猜想，在新的情境中舉一反三，解決一些復雜的問題，對數學知識提出改革建議．創造性理解是超越關系理解的更高級的理解，具有創新的特征．創造性理解水平有以下表現形態．

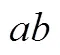
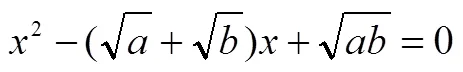
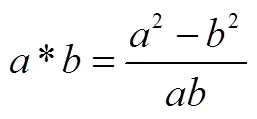
理解數學拓展抽象的意義．學生能夠以已有知識、經驗或體驗為基礎，獲取新的知識、經驗或體驗，自我認識、自我反思、自我完善、自我超越、自我創造，成為思考者、發現者、發明者、創新者．學生數學學習的結果，除了獲得知識和技能外，還有長時間積累后形成的創新思維模式，達到孔子所說的“從心所欲不逾矩”的境界．如“你能類比兩個數的均值不等式，猜測出3個、4個等更多數的均值不等式嗎？”學生能夠遵循數學知識發展的內在邏輯，擴充均值不等式的維度，升華為個正數的均值不等式．

理解數學在實踐中的應用．學生能夠將現實中的問題轉化成數學模型，在數學與現實的循環中不斷生成和重構知識．數學源于現實、寓于現實并應用于現實，應用化的精神是數學的生命，根植于現實中的數學充滿著生機活力．如“我們生活中哪些最值問題可以用均值不等來處理？”機器人興趣小組組長張玉瓊（化名）以建機器人場地為背景提出真實的研究問題：“要在科技活動室用屏風圍出一個矩形機器人活動場地．（1）若矩形場地的面積為6.25 m2，問這個矩形的長和寬各為多少時，所用屏風最少？最少要購買屏風長多少米？（2）現有屏風長為10 m，問這個矩形活動場地的長和寬各為多少米時，屏風圍成活動場地的面積最大？最大面積是多少平方米？”此問題來源于校園真實科技生活，學生能夠很快進入研究角色．教育家蘇霍姆林斯基說：“智慧出在人的手指尖上，實踐操作不僅僅是身體的動作，而且是與大腦的思維活動緊密聯系著的．”[22]解決活動場地中的數學最值問題，激發了學生的創新熱情．

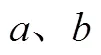
3.4 文化性理解水平

文化性理解水平的學生，能夠理解數學史對觀念、精神、思維方式等產生的影響，受到數學家優秀品格的熏陶，進行數學文化的欣賞，在追求數學美的過程中來加深對數學的理解．阿恩海姆指出，一旦達到了對某一范式最簡單的理解，它就會顯得更穩定、有更多意義、更容易掌握．具有秩序、統一的事物更符合知覺簡化性傾向，更易于使人產生審美體驗[23]．狄德羅曾指出，數學中所謂美的問題，是指一個難于解決的問題，所謂美的解答，是指一個對于困難復雜問題的簡易解答[24]．文化性理解水平有以下表現形態．

理解數學歷史發展的脈絡．學生知道數學概念、定理與歷史上哪些大事件、關鍵人物相關，能夠說數學故事，提煉故事中蘊含的數學思想方法，挖掘故事中孕育的數學精神，注入數學文化意義．如學生知道第24屆國際數學家大會2002年在北京國際會議中心隆重舉行，會標是以三國時期吳國數學家趙爽的弦圖為基礎設計的，趙爽的弦圖不僅能夠證明勾股定理，還能夠探究得到均值不等式．

理解數學的人文價值．學生知道數學概念、定理蘊藏的德育價值、人文關懷．如關于均值不等式中等號何時取，學生能用自己父母年齡做實例加以說明．當父母年齡恰好相同時取等號，當父母年齡不同時取絕對不等號，這說明學生關注父母的年齡和生日，有很好的教育意義．

4 數學理解層次劃分的反思

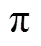
學生數學理解水平劃分還可做進一步探討．為便于操作，采用了工具性理解、關系性理解、創造性理解、文化性理解4個水平的劃分方法．工具性理解、關系性理解、創造性理解水平是逐步提高的，這三者主要體現在學生認知領域的遞進關系．而文化性理解水平主要是體現在情感、態度、審美、意志、價值觀領域，是不可或缺的一種理解水平．事實上，可以將學生數學理解的水平劃分為兩個維度，即認知維度的數學理解水平、情感維度的數學理解水平，在它們的交叉點做更加深入的研究．

學生數學理解水平是發展變化的、有差異的．數學概念的形成和關系的建立具有層次性，因而數學理解不是一蹴而就的，具有動態性、階段性、漸進性等特征．要接受學生數學理解的差異性，讓學生在突破自我中努力達到自己潛在的最高理解水平．在力所能及的范圍內，鼓勵學生追根問底式的深層次學習，摒棄浮光掠影式的表層次學習，達到“關系理解”的水平；鼓勵學生對知識的自我建構，達到“創造性”理解水平；鼓勵學生在數學的歷史文化中進行熏陶，達到“文化性理解”的水平．

[1] National Council of Teachers of Mathematics. Principles standards and for school mathematics [M]. Reston V A: NCTM, 2000: 18.

[2] Skemp R. The psychology of learning mathematics [M].London: Penguin Books, 1971: 46.

[3] HIEBERT J, CARPENTER T. Learning and teaching with understanding [M] // Douglas A Grouws. Handbook of research on mathematics teaching and learning,New York: Macmillan, 1992: 65–97.

[4] GREENO J. Understanding and procedural knowledge in mathematics instruction [J]. Educational Psychologist, 1978, 12 (3): 262–283.

[5] 余瑤，張春莉．國外數學理解研究的進展與展望[J]．教育學報，2018，14（1）：35–44．

[6] SIMON M. Key development understandings in mathematics: A direction for investigating and establishing learning goals [J]. Mathematical Thinking and Learning, 2006, 8 (4): 359–371.

[7] MAYER R. Models for understanding [J]. Review of Educational Research, 1989, 59 (1): 43–64.

[8] Skemp R. Relational understanding and instrumental understanding [J]. Mathematics Teaching, 1976, 77 (3): 20–26.

[9] BUXTON L. Four levels of understanding [J]. Mathematics in School, 1978, 7 (9): 36–38.

[10] Biggs J B, Collis K F. Evaluating the quality of learning: The SOLO taxonomy [M]. New York: Academic Press, 1982: 13–15.

[11] BIGGS J, WATKINS D. Classroom learning [M]. Singapore: Prentice Hall, 1995: 176.

[12] GREENO J, RILEY M. Processes and development of understanding: In metacognition, motivation, and understanding [M]. Hillsdale: Lawrence Erlbaum Associates, 1987: 293.

[13] 吳駿．小學四年級學生對平均數概念理解的發展過程[J]．數學教育學報，2011，20（3）：39–41．

[14] WIGGINS G, MCTIGHE J. Understanding by design [M]. VA: Association for Supervision and Curriculum Development, 2005: 85–100.

[15] SAWYER R K. The Cambridge handbook of the learning sciences [M]. NewYork: Cambridge University Press, 2006: 2.

[16] Usiskin Z. What does it mean to understand some mathematics [R]. ICME-12, Seoul, 2012: 10–15.

[17] 鞏子坤．數學理解說及其理論與課程意義[J]．比較教育研究，2009，31（7）：39–43．

[18] 徐彥輝．數學理解三種方式及其課堂教學特征[J]．中國教育學刊，2012（1）：59–61．

[19] 匡金龍，包靜娟．為理解而設計——促進小學生數學理解的教學策略研究[J]．上海教育科研，2013（11）：61–63．

[20] 王瑞霖，綦春霞．數學理解的五層遞進及教學策略[J]．中國教育學刊，2014（12）：40–45．

[21] 谷曉沛，馬云鵬，朱立明．高一學生函數概念數學理解水平的實證研究——以T城市為例[J]．數學教育學報，2018，27（3）：25–29．

[22] 蔡健飛．小學生數學創新思維的培養[D]．武漢：華中師范大學，2007：45．

[23] 朱黎生，宋乃慶．格式塔美學對數學教學的啟示[J]．數學教育學報，2012，21（6）：10–12．

[24] 陳煥斌，張雄．略論數學美的本質屬性[J]．數學教育學報，2008，17（5）：28–30．

The Division of the Level of Mathematical Understanding

LI Chun-lei1, 2, YU Feng-lai3

(1. Faculty of Education, Beijing Normal University, Beijing 100875, China；2. Liang Xiang High School Affiliated to Beijing Normal University, Beijing 102488, China;3. Yanzhuang Street Central Junior Middle School of Ju County, Shandong Rizhao 276535, China)

Based on the interpretation of the connotation of classical mathematical understanding and the division of existing understanding levels, students’ mathematical understanding is divided into four levels: instrumental understanding, relational understanding, creative understanding and cultural understanding. Taking the mean value inequality as a typical case, this paper interprets the connotation and manifestation of students’ various levels of mathematical understanding in detail.The value of the level of instrumental understanding cannot be ignored. The level of students' individual mathematical understanding is developing and changing, and the level of students’ mutual mathematical understanding is different. Within the scope of the ability, students are encourage to pursue in-depth learning, to achieve the level of “relational understanding”. Students are encouraged to self-construct knowledge and to achieve the “creative understanding” level; they are encouraged to be nurtured in history and culture, aesthetic taste and humanistic care, so as to reach the level of “cultural understanding”.

mathematical understanding; instrumental understanding; relational understanding; creative understanding; cultural understanding

2022–04–09

北京市教育學會“十四五”教育科研課題——基于高階能力培養的大單元教學課程設計研究（FSYB2021-002）

李春雷（1967—），男，河北香河人，正高級教師，博士，主要從事數學教育和學生創新能力發展研究．

G447

A

1004–9894（2022）04–0068–06

李春雷，于鳳來．數學理解水平的劃分[J]．數學教育學報，2022，31（4）：68–73．

[責任編校：陳雋、陳漢君]