數學循環論證的思考及其價值展望

李鋒雷，孔德宏

數學循環論證的思考及其價值展望

李鋒雷，孔德宏

（云南師范大學 數學學院，云南 昆明 650050）

循環論證的核心問題是推理過程中的邏輯是否嚴謹．數學證明的過程是否為循環論證，根據不同的標準，有不同的結果．以學科體系、教材體系為標準，得到4種體系下的循環論證：（1）同一教材體系；（2）不同教材體系；（3）同一學科體系；（4）不同學科體系．循環論證所帶來的價值有很大的應用前景：能夠讓知識的學科價值更加充分發揮，能夠降低學生負擔．未來教材改革應關注：（1）教材改革應兼顧知識的學術邏輯與學生的心理邏輯；（2）教材改革應注重教育邏輯的完善；（3）教材改革可考慮從循環論證根源的剖析上攝取“營養”．

循環論證；教材體系；跨學科體系；核心素養；教材改革

1 問題提出

“循環論證”一詞最早出自于亞里士多德《分析前篇》第十四節，“循環論證”是指用來證明論題的論據本身的真實性要依靠論題來證明的邏輯錯誤．其邏輯結構可歸納為兩類：①對于命題，蘊含，假設成立，所以成立；②對于命題、、，蘊含，蘊含，蘊含，假設成立，所以成立，所以成立，所以成立．關于數學證明過程中的循環論證，張景中院士曾有過精辟論述：“孤立地看待一個命題的證法，很難肯定它是否犯了‘循環論證’的錯誤．”[1]究其原因，在于數學證明過程是否存在循環論證的錯誤，依據不同標準，有不同的判定結果．剖析循環論證產生的根源，可以歸納出4種體系下的循環論證：（1）同一個教材體系中，條件到結論的推導有多種途徑，同一個命題的證明，途徑a是循環論證，途徑b則不是；（2）不同的教材體系中，不同知識體系下的知識點出現的先后順序不同，致使同一個證明過程在A知識體系下是循環論證，在B知識體系下又不是了；（3）同一學科體系中，現階段知識的嚴謹證明需要用到后階段的知識，然而現階段學生的認知水平不夠，不能講授后階段的知識，導致循環論證；（4）不同學科體系之間，數學學科本身是一個十分嚴謹的公理化體系，數學定理不以其它學科的規律或者原理為依據，從而用其它學科的規律或原理來證明數學定理導致了循環論證．數學證明中的循環論證與學生的邏輯推理等核心素養息息相關，具有重要的學科價值．同時“循環論證”各種類型產生的根源與教材知識結構有著緊密的聯系，結合人教版普通高中教科書數學2019版（以下簡稱新教材）以及地方版本教材，通過對其深入研究，為教材改革提供新的方向[2]．

2 幾種循環論證類型的剖析

以學科體系、教材體系為標準，對數學上的循環論證進行分類剖析，可以得到以下4類情況．

第一，同一個教材體系中的同一個命題的證明，途徑a是循環論證，途徑b不是．

（1）函數()=2單調性不同證明途徑的剖析．

考慮到學生已有的認知水平，高中階段指數函數單調性的“證明”教學中，僅是根據觀察圖象的上升、下降趨勢來得出的．這種方法在邏輯上是不嚴謹的，教學中可以通過作商法對其單調性進行補充證明，但同樣是作商法，途徑a犯了循環論證的錯誤，途徑b則沒有，下面呈現證明()=2單調遞增的兩種途徑．

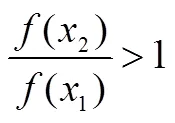
說明①：途徑a是通過作商比較(1)和(2)的大小，從而得出函數()=2的單調性，但這里1=20<2用到了指數函數()=2的單調性，故用單調性證明單調性，犯了循環論證的錯誤．

說明②：這里換一種角度去思考：判定上述證明過程犯了循環論證的錯誤是因為它用到了指數函數的單調性．在新教材必修第一冊第三章第三節（第89頁）學到了冪函數，而指數函數在第四章學習，故可以繞過指數函數單調性而選擇冪函數的單調性進行證明，則避免了循環論證，將其證法改寫為：

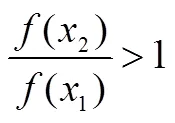
圖1 作差法證明函數增減性

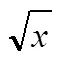
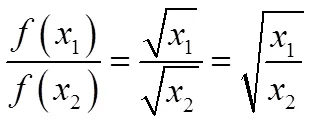
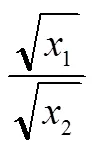
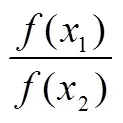
從以上分析可知，在同一教材體系中，命題與結論推導的途徑具有多樣性[3]．同一個命題的證明，一條途徑是循環論證，走另一條又不是了．

第二，不同教材體系下，同一個證明在A知識體系下是循環論證，在B中則不是．

（1）三角恒等式證明勾股定理的剖析．

現有的教材體系中，初中學習勾股定理，高中學習三角恒等式，下面給出勾股定理的一種證法．

證明：三角恒等式證明勾股定理

說明①：在現有的教材體系中（以人教版教材為例），勾股定理是在八年級下冊學習的，而三角恒等式是在高中學習的，且三角恒等式的證明用到了勾股定理，這樣的證明自然是犯了循環論證的錯誤的．

說明②：但是在張景中院士提出的“新中學三角體系”中[4-5]，利用“面積法定義正弦”，得到正弦和角公式，再通過正弦和角公式得到三角恒等式，最后得到勾股定理，其簡要邏輯體系如圖2所示．

圖2 中學教材體系

從圖2可知，在原來的教材體系中，勾股定理是知識的“生長點”，三角恒等式是知識的“延伸點”，但是在張景中院士的體系中，則反之．這樣一來，上述證明在不同的教材體系中，其循環論證的判定結果也不同．

（2）向量法證明勾股定理的剖析．

在新教材必修第二冊第六章平面向量及其應用后安排了一個數學探究（第63頁）：用向量法研究三角形的性質，探究活動的引言部分是用向量法推導勾股定理，如圖3．

圖3 用向量法推導勾股定理

說明①：平面幾何證明勾股定理時，需要添加輔助線、構造正方形等，不僅復雜，而且不容易想到，使用向量法則可以避免這些．這樣的安排似乎是十分合理的，但正如張景中院士所說，對其進行尋根問底的追問，則又是循環論證了．新教材必修第二冊第6頁的“閱讀與思考”中介紹了向量及向量符號的由來，向量最初應用于物理學，被稱為矢量，如力、位移、速度、電場強度、磁感應強度都是向量……向量是一種帶幾何性質的量，向量的加法（即平行四邊形法則）在物理上是指合力是由兩個（及以上）的分力進行合成，合成過程中用到了正交分解，而正交分解則用到了勾股定理，故用向量法證明勾股定理在一定意義上也是一種循環論證．

說明②：從上述討論中，基于新教材體系，一定意義上可以認為向量法證明勾股定理是犯了循環論證的錯誤的，但換一種體系來看，則又不是了．判斷其犯循環論證的錯誤是基于物理學中力的合成用到的正交分解，而在數學上是直接定義了向量的加法、減法從而得到向量的平行四邊形法則的，故這樣來看，用向量法證明勾股定理是沒有犯循環論證的錯誤的，如在滬教版教材體系中，初中教材就定義了平面向量及其加減運算，并在教材中初步介紹了用向量工具證明幾何問題．

第三，同一學科體系中，現階段知識的嚴謹證明需要借助后階段的知識導致循環論證．

在基礎教育階段普遍存在著這樣一種現象，基于學生的認知水平，一些現階段的數學知識不可能得到嚴格的證明，如前面談到的指數函數單調性證明就是如此，因為高中階段是無法嚴格定義無理指數冪的，而指數函數定義域又是全體實數，故無法在高中階段給出其函數單調性的嚴格證明．

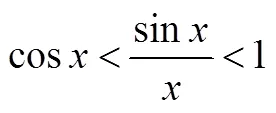
說明①：上述證明過程用到了圓面積公式：

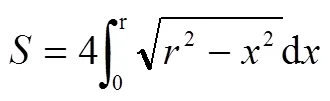
顯然，在這個過程中，也用到了(sinx)′=cosx，從而用到了極限，因此是犯了循環論證的錯誤．也有學者通過其它方法[7]來避免使用極限及其推論來得到圓面積公式，從而排除了利用不等式時產生循環論證的可能，但本質上都用到了（單位）圓周長度的存在性．復旦大學樓紅衛教授于2017年在《大學數學》上發表了有關論述，他認為：弧度的建立依賴于單位圓周是可求長的，而極限的討論基于單位圓周長的定義，更確切地說，需要基于定積分的理論．因此，尋求講授定積分理論前給出的嚴格證明并不現實[8]，具體證明過程可參閱文獻[8]．

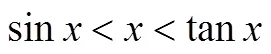
第四，不同學科體系中，數學定理不以某個物理規律的正確性作為自己成立的條件．

跨學科素養長期以來都是學者所熱衷的話題，其意義也顯然，學科與學科之間的碰撞產生的火花，對提高學生的學習興趣具有重要意義．數學與物理學這兩個學科之間的聯系就十分密切，這兩個學科如何產生火花，一些文獻就有談到．如一篇文章就談到了“用物理方法證明正弦定理和余弦定理”[10]，下面為其簡要證明過程．

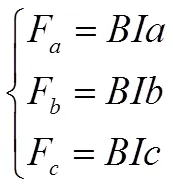
“很顯然，這3個力是相互平衡的共點力”，其作用線相交于三角形ABC的外心O．以O為原點，對Fa、Fb、Fc進行正交分解，如圖5所示．

分別得到：

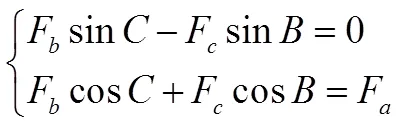
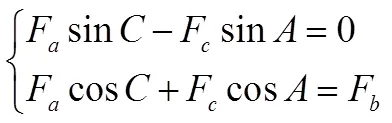
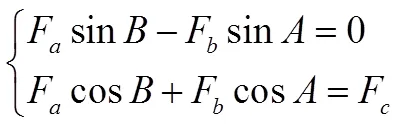
聯立（1）、（2）、（3）、（4）得到：

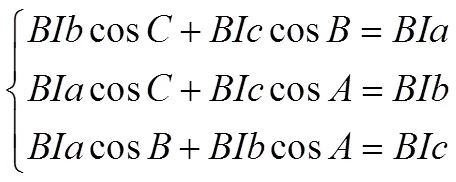
分別化簡（5）、（6）即得正弦定理、余弦定理．

說明①：上述證法看似沒問題，但在“很顯然，這3個力是相互平衡的共點力”處犯了循環論證的錯誤[11]．數學中用來說明三角形邊角關系的正弦定理成立與否，直接決定了這個3個力是不是平衡力，其簡要證明過程如下（正弦定理與余弦定理等價，故以正弦定理為例）．

對線框所收受到的力進行分解（只標出分力的方向，未標出其大小），如圖6所示．

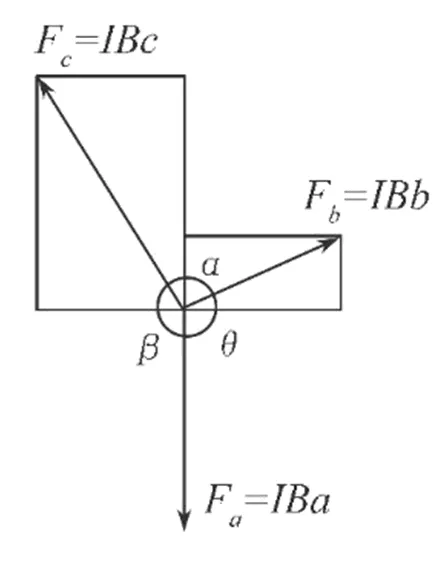
圖6 受力分解

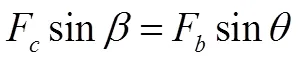
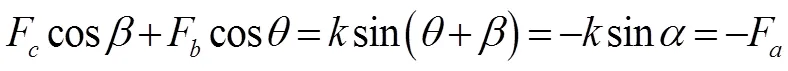
即垂直方向上，F與F在垂直于F作用線上的分力大小相等，方向相反；平行方向上，F與F在平行于F．作用線上的分力大小之和等于F，方向相反．

說明②：從上述證明過程分析得到，若正弦定理不成立，則上述結論中的等式（7）、（8）至少有一個不成立，從而使得F、F、F合力就一定不為0，即不是平衡力.故用物理原理證明正弦定理，其本質上還是用到了正弦定理，故犯了循環論證的錯誤．

這說明在不同學科體系中，數學是可以脫離其它具體學科而獨立發展的．數學學科本身是一個十分嚴謹的公理化體系，所有的數學定理，都不會以某個物理原理或物理規律的正確性作為自己成立的條件，從而用其它學科的規律或原理來證明數學定理就會導致循環論證．

3 循環論證的價值分析與展望

3.1 知識體系的“變動”所帶來的價值分析

教材是教育得以進行的基本條件，在整個人才培養過程中占有十分重要的位置．習近平指出：“學科體系與教材體系密不可分．學科體系建設上不去，教材體系就上不去；反過來，教材體系上不去，學科體系就沒有后勁．”數學教材往往是數學課程發展、研究過程以及整個數學教育史中最為可靠和重要的歷史見證[12-13]．不同的教材體系對學生的學習是有不同的影響和價值的[14]，在剖析循環論證產生根源的過程中分析得到，在不同教材體系中知識點先后的順序是不同的，致使條件到結論的推導途徑不同，從而可能導致循環論證．這樣得到一種新的角度，即通過“變動”數學知識學習的時間順序，不僅可以避免循環論證，更大地發揮知識的學科價值，同時還能減輕學生的負擔，從而完善教材編寫過程中的教育邏輯[15]．故循環論證所帶來的價值有很大的應用前景，這一點在新教材和一些地方版本的教材中就有明顯體現．

3.1.1 讓知識的學科價值更加充分發揮

在新教材中，“解三角形”不再單獨設立章節，而是納入第六章第四節平面向量的應用，其推導途徑也發生了改變，改用向量法推導正弦定理（教材第45頁）．其合理性顯然，向量集數與形于一身，每一種向量運算都有相應的幾何意義，通過向量證明某些幾何圖形的性質，比平面幾何中“從圖形的已知性質推出待證的性質”更為簡便，而且證明過程是程序化的，充分體現了向量運算的作用[16]．這樣的安排，對比舊版教材，更大地發揮了平面向量的幾何價值，既使得“平面向量的應用”這一節內容不再單薄，也加強了向量與平面幾何的聯系，突出了數學學科的整體性．而且更大地發揮了一些知識的學科價值甚至是跨學科價值．雖然這些“變動”的教育價值有待更多的研究去分析論證，但在數學學科價值上已經使得一些數學知識煥發出新的生命力，這是有意義的．

3.1.2 能夠降低學生負擔

新教材必修第二冊第六章安排的數學探究（教材第63頁）：用向量法研究三角形的性質，其探究活動的引言部分是用向量法推導勾股定理，探究活動主要內容是用向量法推導三角形的3條中線交于一點（重心）及其性質．在原來的教材體系中，向量法是在高中學習，而三角形重心及其性質在初中學習．新教材中用向量法推導重心及其性質，這樣安排的價值也很明顯，平面幾何中證明重心的定義時，用到的幾何方法不僅復雜，而且不容易想到，使用向量法不僅可以完全避免這些，同時還能在證明過程中，“順便”得到三角形的一個重要性質（三角形重心是中線的三等分點）．這說明通過“變動”數學知識學習的時間順序得到新的教材體系，繼而得到新的證明方法，既避免了循環論證，又能減少學生的學業負擔．給教材研究者一種新的啟示——將向量“變動”到初中去學習．向量在幾何中的價值，舉足輕重，章建躍認為，初中數學難學源于初中幾何難學[17-18]，數學成績的兩極分化發生在平面幾何的學習中．若是在初中就能夠初步地學習向量，對指導后續的幾何學習是一大助力，這對學生的負擔也是很大的解放．這一點在滬教版初中教材（2007版）中就有體現，在第二十二章第四節就學習了平面向量及其加減運算，并在章末的閱讀材料（第118頁）中初步介紹了用向量法證明幾何問題．

3.2 知識體系的“變動”對未來教材改革的展望

各科教材知識體系的構成，都有其內在的邏輯，總體來看，教材的編寫邏輯表現有3個方面．其一是學術邏輯，即根據學科或學術領域知識生成、發展、演變的邏輯來編寫，其表現形式為由易到難、由淺至深，所注重的是知識與知識之間的相互聯系，保持知識的銜接順序，使教材內容有條不紊、井然有序．其二是心理邏輯，根據這一邏輯，教材編寫主要是根據學生的學習興趣、認知水平和認知習慣，以學生易于接受、樂于接受、能夠接受為導向．其三是教育邏輯，即把學術邏輯和心理邏輯結合起來，使教學內容既兼顧學科知識的關聯性，又有利于學生學習掌握[19]．

3.2.1 教材改革應兼顧知識的學術邏輯和學生的心理邏輯

新教材中向量法證明“解三角形”中的一些定理，相比于一些方法確實具有簡便性，但教材的編排順序發生了改變．在原來的教材中，正弦定理的學習先于余弦定理，在新教材中，則反之．這樣的安排是考慮了向量數量積運算中出現了角的余弦，故先學余弦定理，再學正弦定理．同時教材中也指出探索和證明這兩個定理的方法很多，有些方法比向量法更簡潔，而且先學余弦定理，再學正弦定理，也沒有體現學術邏輯中由易到難的表現形式，究其原因，在于教材編排要考慮其知識結構的整體性．受限于此，這樣的安排總是有種美中不足的感覺，故在未來的教材改革中，可以考慮兼顧知識體系的整體性，又能優化正弦定理的推導方法．即兼顧知識的學術邏輯和學生的心理邏輯．

3.2.2 教材改革應注重教育邏輯的完善

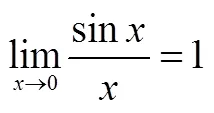
3.2.3 教材改革應在循環論證根源的剖析上攝取“營養”

從某種意義上來說，新教材中的這種“變動”，使得一個數學證明是否循環論證的界定結果發生了改變，反之，對循環論證的研究可以“反哺”，從而促進教材“變動”．循環論證的類型有很多，目前的新教材中也未涉及，新教材作為一種風向標，效仿新教材的一些“變動”，考慮把循環論證的各種類型納入未來教材中的探究活動、閱讀材料甚至是教材內容，對發展學生數學核心素養、促進未來教材改革具有重要意義．這樣的展望是合理的，這是因為教材改革本身就要兼顧知識的學術邏輯與學生的心理邏輯．循環論證產生的根源與知識的學術邏輯息息相關，教材的“變動”則考慮的是學生的心理邏輯，這二者相輔相成，故教材改革可以考慮從循環論證根源的剖析上攝取“營養”．

4 結語

數學作為一門邏輯科學，一個數學證明過程是否循環論證，其判定結果隨著體系的不同而不同：循環論證可以在同一教材體系討論，也可以在不同教材體系討論，甚至可以在不同學科體系討論．究其原因，在于其它學科的一些原理或是規律的正確性是以相關的數學定理為依據，而數學學科本身是一個十分嚴謹的公理化體系，從一些不加定義的原始概念以及一些不需要證明的公理出發，按照一定的邏輯法則將知識系統化，最后形成一個螺旋上升的有機整體[20]．循環論證的研究正是“寄生”于這樣一種有機的整體，其研究的生命力自然旺盛．經過多年的實踐，中國高中數學教材已具有一定的系統性．為適應時代的發展，體現新的教育教學理念，依據課程標準，其改革可在落實立德樹人根本任務、體現核心素養、創新呈現方式、關注師生體驗等方面進行創新探索與實踐[21]．這給數學教育研究者一種新的啟示或提供了某種新的視角[22]，基于學科本身特性的研究可以達到更大的認識深度，循環論證的研究價值有待更多學者去挖掘．

[1] 彭翕成．也談“循環論證”[J]．數學教學，2008（2）：27-28．

[2]鄧翰香，吳立寶，曹一鳴．新世紀以來我國中小學數學教材研究熱點、演進與展望——基于科學知識圖譜的實證分析[J]．教育理論與實踐，2021，41（8）：38-43．

[3]章建躍．“預備知識”預備什么、如何預備[J]．數學通報，2020，59（8）：1-14．

[4]李鋒雷，胡恩良．“新中學三角體系”概述及其進一步思考[J]．中學數學雜志，2021（1）：19-22．

[5]張景中．重建三角，全局皆活——初中數學課程結構性改革的一個建議[J]．數學教學，2006（10）：1-4．

[6]華東師范大學數學系．數學分析（上冊）[M]．4版．北京：高等教育出版社，2010：57．

[7]劉華民．關于重要極限lim→0 (sin/)=1證明與講授方法的注記[J]．大學數學，2010，26（S1）：75-77．

[8]樓紅衛．關于極限lim→0 sin/的注記[J]．大學數學，2017，33（3）：107-110．

[9]華東師范大學數學系．數學分析（上冊）[M]．5版．北京：高等教育出版社，2019：53．

[10]徐英．用物理方法證明正弦定理和余弦定理[J]．中學數學雜志，2006（9）：17-18．

[11]王偉民．再談“用物理原理證明數學問題”是在“循環論證”[J]．中學數學雜志，2018（1）：63-65．

[12]張昆．高校文科專業教材建設的辯證思考[J]．高等教育研究，2020，41（11）：73-80．

[13]朱雁，倪明，孔令志，等．數字時代中的數學教材研究與開發及使用——第三屆國際數學教材研究和發展會議綜述[J]．數學教育學報，2020，29（2）：94-99．

[14]習近平．習近平談治國理政（第二卷）[M]．北京：外文出版社，2017：345-346．

[15]史寧中，呂世虎，李淑文．改革開放四十年來中國中學數學課程發展的歷程及特點分析[J]．數學教育學報，2021，30（1）：1-11．

[16]人民教育出版社，課程教材研究所中學數學課程教材研究開發中心．普通高中教科書數學（必修第二冊）[M]．北京：人民教育出版社，2019：63．

[17]伍春蘭，丁明怡，王肖．在“推知”活動中涵養邏輯推理素養——以“線面垂直”的概念和判定為例[J]．數學通報，2020，59（4）：24-27，31．

[18]章建躍．研究三角形的數學思維方式[J]．數學通報，2019，58（4）：1-10．

[19]別敦榮，王根順．高等學校教學論[M]．北京：高等教育出版社，2008：1．

[20]杜劍南，趙戌梅．基于“關鍵詞”視角的2017版與實驗版《普通高中數學課程標準》的比較研究[J]．數學教育學報，2020，29（6）：61-68．

[21]龍正武，高存明，王旭剛．高中數學教材改革的創新與實踐[J]．課程·教材·教法，2020，40（7）：86-91．

[22]鄭毓信．新一代數學教育研究者的成長[J]．數學教育學報，2020，29（6）：1-6．

Thinking and Value Prospect of Mathematical Circular Argument

LI Feng-lei, KONG De-hong

(Faculty of Mathematics, Yunnan Normal University, Yunnan Kunming 650500, China)

The core problem of circular argument is whether the logic in the reasoning process is rigorous. Whether the process of mathematical proof is a circular argument or not has different results depending on different criteria. The circular argument under the four systems can be obtained taking the discipline system and the textbook system as the standard: (1) the same textbook system; (2) different textbook systems; (3) the same discipline system; (4) different discipline systems. The value brought by circular argument has great application prospects: it can make the disciplinary value of knowledge more fully utilized and reduce the burden on students. This paper puts forward some thoughts for the future reform of textbooks: (1) The reform of teaching materials should take into account the academic logic of knowledge and the psychological logic of students; (2) the reform of teaching materials should focus on the improvement of educational logic; (3) the reform of teaching materials should consider ingesting “nutrition” from the analysis of the root cause of circular argumentation.

circular argument; teaching material system; interdisciplinary system; core literacy; reform of the teaching material

G423.3

A

1004–9894（2022）04–0074–06

李鋒雷，孔德宏．數學循環論證的思考及其價值展望[J]．數學教育學報，2022，31（4）：74-79．

2022–03–22

云南省學位委員會2019—2021年“中學數學解題研究案例庫”項目（04400205020502133）；云南師范大學研究生核心課程建設項目——數學課程與教材研究（YH2018-C06）

李鋒雷（1997—），男，江西上饒人，碩士生，主要從事數學教育與數學教材研究．孔德宏為本文通訊作者．

[責任編校：陳漢君、陳雋]