新型SRC柱-H型鋼梁組合節點有限元分析

喬光德，劉繼明，吳成龍，譚文婭，王傳貽，張祥威

(青島理工大學 土木工程學院，青島 266525)

近年來，國家對預制裝配式建筑結構的大力推廣，使預制裝配式框架結構的抗震研究成為了國內外學者關注的重點，型鋼混凝土柱和鋼梁作為一種組合結構，由于其良好的抗震性能被廣泛應用于裝配式建筑結構中梁柱節點的連接。

SALVATORE等[1]通過試驗測試發現鋼-混凝土復合結構能夠合理地利用材料且具有很高的預制能力，可以提供高水平的延展性和耗能能力。DENG等[2]介紹了一種完全預制的梁-柱節點，其中包含復合鋼超高性能混凝土，通過試驗研究發現節點具有良好的承載力和抗震性能，并為梁柱節點連接提出了理論模型。WU等[3]提出了一種新型的模塊化預制復合接頭，研究低周往復循環荷載作用下3個不同剛度比試件的失效過程和特性，發現該新型復合接頭具有較高的承載能力和良好的抗震性能。蘆靜夫等[4]利用ABAQUS對新型裝配式鋼-混組合梁柱節點進行有限元數值模擬，結果發現：該新型節點在多遇地震作用下承載力較好，受力性能優異，且節點連接高效，可提高裝配效率。張健新等[5]對工字鋼、對拉螺栓和方鋼管3種不同連接形式的新型裝配式鋼混框架中節點進行低周往復荷載試驗，發現方鋼管連接形式的試件有著最高的累積耗能能力、承載能力和變形能力，且破壞形態最優。張愛林等[6]發現端板式裝配式梁柱連接節點可以有效控制翼緣連接板剛度變化，利用翼緣連接板導致的變形去消耗地震能量，從而保證梁柱等主要構件不發生破壞。程萬鵬等[7]對預制裝配式部分鋼骨混凝土框架結構梁柱節點進行試驗研究，發現該節點比普通鋼筋混凝土節點承載力高2～3倍，且承載力退化速率較慢，在保持高承載力的同時還具有較好的延性。劉震等[8]對預制裝配式H型鋼骨混凝土柱-柱連接的節點進行有限元受力分析，發現該節點的初始剛度、承載力和延性性能較好，且軸壓比和剪跨比對節點的靜力性能影響顯著。王燕[9]闡述過塑性鉸外移的必要性，通過“強柱弱梁，強節點”的設計思想使梁端出現塑性鉸，從而形成較大的變形能力和耗能能力。郭子雄等[10]對新型裝配式鋼筋混凝土柱-鋼梁框架節點進行低周反復荷載試驗，發現該節點的破壞模式均是梁端出現塑性鉸，通過梁絞機制破壞來充分耗能。

目前，預制鋼-混凝土復合結構組成梁柱節點的抗震性能方面的研究較少。因此，本文在課題組前期擬靜力試驗研究的基礎上，采用ABAQUS軟件對新型SRC柱-H型鋼梁組合邊節點進行數值模擬，得到的滯回曲線、骨架曲線和破壞形態與試驗曲線吻合較好，說明了有限元模型的可行性，進而分析節點蓋板長度和柱軸壓比2個參數變量對該節點抗震性能的影響。

1 試件概況

1.1 試件設計與制作

新型SRC柱-H型鋼梁組合邊節點的設計如圖1所示，主要由預制的SRC柱、H型鋼梁和節點核心區模塊3部分組成，試件所用型鋼均為Q355B，SRC柱的截面尺寸為350 mm×350 mm，主要由H型鋼骨HW150 mm×150 mm×7 mm×10 mm，4根直徑20 mm的HRB400級縱筋，直徑8 mm的HPB300級箍筋，以及外包C40混凝土組合而成；鋼梁尺寸為280 mm×150 mm×10 mm×10 mm；上下柱和節點核心區模塊通過M20的S10.9級摩擦型高強螺栓連接；鋼梁和節點核心區模塊采用同級別的M24摩擦型高強螺栓連接；在施工現場通過栓焊混合連接的方式進行快速裝配，在達到裝配快捷的同時，也能滿足“強柱弱梁”的抗震設計原則。

圖1 新型SRC柱-H型鋼梁組合節點(單位：mm)

1.2 加載裝置和加載制度

本次試驗依照規程[11]中荷載-位移控制的方法進行加載，試件的屈服荷載根據理論計算確定，屈服之前采用荷載控制，屈服之后位移控制；試件加載至梁端載荷下降為85%的峰值荷載或者試件有明顯破壞現象時，停止試驗。加載裝置和加載制度分別見圖2和圖3。

圖2 試件加載裝置

圖3 加載制度

圖4 材料本構關系

2 有限元模型建立與驗證

2.1 材料本構關系

本文所用的型鋼均為Q355B，彈性模量為2.06×105MPa，密度為7.85×103kg/m3，泊松比取為0.3，鋼材、螺栓均采用簡化處理的二折線本構模型[12]，材料的本構關系見圖4。型鋼、螺栓和鋼筋在計算中均使用Von-Mises屈服準則及相關聯的流動法則。混凝土采用塑性損傷模型，其本構關系基于規范[13]建議的應力-應變曲線。

2.2 網格劃分及相互作用

本模型中縱筋和箍筋采取T3D2單元進行網格劃分，其余部件采用C3D8R單元，以保證求解的精確度。由于試驗中試件的變形主要在節點核心區附近，故方鋼管、節點蓋板、翼緣連接板和腹板等厚度方向至少劃分2個網格單元；節點核心區和上下柱及梁之間通過螺栓的預緊力進行連接，M24和M20高強螺栓的預緊力分別是255和155 kN，螺栓網格劃分精細；上下柱縱筋外伸至節點核心區的部分采用“等效螺栓”進行替代，等效螺栓的材料屬性設置為縱筋的屬性，兩者之間采用“耦合”的方式進行約束連接；節點蓋板和梁翼緣部分通過翼緣連接板進行“綁定”約束來模擬試件中的焊接，螺栓和螺栓孔之間采用“表面-表面”接觸，考慮到螺栓和螺栓孔之間存在間隙，為調整區域指定容差設置為1，其余“表面-表面”接觸均設為0.1，接觸的摩擦系數為0.35，有限元網格劃分和邊界條件設置見圖5。

圖5 有限元網格劃分和邊界條件設置

2.3 邊界條件

ABAQUS數值模擬所建立的邊界條件要與試驗相一致，本模型先在梁端部創建參考點RP1，上柱頂面中心位置為RP2，柱底面中心位置為RP3，通過耦合的方式將這3個需要運動的面進行約束。其中梁端加載端RP1的y位移方向和x，z轉角方向進行約束限制；柱頂RP2的x，y位移方向和x，z轉角方向進行約束限制；柱底RP3的x，y，z位移方向和x，z轉角方向進行約束限制。軸壓力所需的集中荷載通過參考點RP2施加在柱頂面的中心位置，模型的低周往復循環荷載加載點設置在梁端參考點RP1，以此來和試驗的邊界條件相對應。

2.4 有限元模型驗證

由圖6可見，試驗和模擬的破壞形態均是在翼緣連接板處形成塑性鉸，受壓側的翼緣連接板屈曲變形，受拉的一側撕裂變形，兩者的破壞模式相近說明了模型的可行性。

圖6 破壞形態對比

試驗和模擬的滯回曲線對比見圖7，可見兩者結果吻合較好。兩者曲線整體較為飽滿，呈現梭形，反映出其塑性變形能力較好，具有良好的耗能能力；加載初期，兩者都處于彈性階段，荷載-位移曲線基本成線性增加，隨著位移加到25 mm后，滯回曲線包圍的面積開始加大，說明試驗和模型耗能增加；加載后期，試件的強度、剛度退化較快，模擬時由于材料屬性和邊界條件設置過于理想化，所以模擬曲線總體上比試驗曲線更為平滑和飽滿。圖8是試驗和模擬的骨架曲線對比，可見兩者曲線走勢基本一致，均有著明顯的彈性、強化和破壞3個階段。滯回曲線和骨架曲線與試驗結果相近進一步驗證了模型的準確性。

3 有限元參數分析

3.1 節點蓋板長度對抗震性能影響

考慮到節點蓋板長度(Length of Joint Cover，簡稱JCL)取值的不同會影響到塑性鉸的位置，本文在節點蓋板長度a為250 mm的BASE試件基礎上模擬了150 mm(JCL-1)、200 mm(JCL-2)、300 mm(JCL-3)和350 mm(JCL-4) 4個長度，進一步探究節點蓋板長度對試件抗震性能的影響。

3.1.1 骨架曲線和特征點分析

參數JCL模型的骨架曲線見圖9，用“能量等值法”在骨架曲線上求出屈服位移Δy，峰值荷載Pm的85%為破壞荷載Pu，對應位移為破壞位移Δu，平均延性系數μ取試件的破壞位移Δu與屈服位移Δy的比值，各特征點均是取正負向循環的平均值，特征點值匯總于表1。

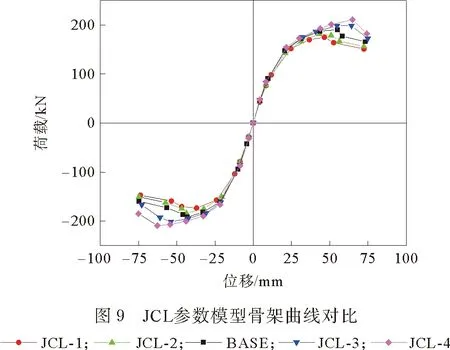
表1 節點模型的特征點值匯總

圖10 等效黏滯阻尼系數ζeq計算示意

從表1和圖9可知，各模型在彈性階段基本一致，隨著節點蓋板長度的增加，JCL-4模型相較于JCL-1模型屈服位移和屈服荷載分別增加了27.4%和16.7%，JCL-4模型相較于JCL-1模型峰值位移和峰值荷載分別提高了52.6%和20.6%，JCL-4模型相較于JCL-1模型破壞位移和破壞荷載分別增加了8.6%和21.4%，JCL-4模型相較于JCL-1模型延性減小了17.1%，其主要原因是節點蓋板長度增加，相當于塑性鉸外移距離加大，塑性鉸處的彎矩是恒定的，由V=M/L知，梁加載端距離塑性鉸的位置變小，所以梁加載端剪力加大即承載力變大。

本文采用等效黏滯阻尼系數ζeq來表示試件在地震作用下的耗能能力，ζeq計算公式和示意見圖10，S(ABC+CDA)為滯回曲線最后一級加載位移，第1循環的包絡面積；S(OBE+ODF)為圖中△OBE和△ODF的面積總和。由表1可知，等效黏滯阻尼系數隨著節點蓋板長度的增加而減小，表明試件的耗能能力變差，JCL-1模型相較于BASE模型等效黏滯阻尼系數增加了7.5%，JCL-4模型相比于BASE模型減小了26.4%，節點蓋板長度為350 mm時耗能能力下降最為嚴重。圖11為JCL參數模型達到破壞時的型鋼應力云圖，可見JCL-4模型的節點蓋板和柱節點區端板連接處有一定程度的彎曲變形，此時節點核心區應力增大，容易引起節點域的脆性剪切破壞，說明塑性鉸位置離節點核心區越遠，模型的耗能能力越差。

圖11 JCL參數模型的型鋼應力云圖

3.1.2 強度退化和剛度退化

本文采用強度退化系數λj表示強度退化的特性，該特性可描述為節點承載力在相同級別加載條件下因循環次數增多而降低的現象。

(1)

式中：Pj為第j(取j=1)次循環中的峰值荷載；Pmax為整個循環中的峰值荷載。

圖12為節點蓋板長度對強度退化曲線的影響。從圖中可以看出各模型均有著明顯的對稱性；各模型的強度退化系數在0.6～1.0之間區別較大，其中JCL-1，JCL-2和BASE 3個模型強度退化曲線較為接近，上升段較快，模型屈服較早，達到峰值荷載時的位移較早，峰值荷載后逐步退化；JCL-3，JCL-4模型前期上升段較慢，達到峰值荷載時的位移較晚，峰值荷載后迅速下降；說明節點蓋板長度超過250 mm的模型后期強度退化較快。

本文采用環線剛度Kj來描述剛度退化，表示節點剛度隨著循環加載次數增多而逐漸變小的特性。

(2)

節點蓋板長度對梁端位移-環線剛度曲線影響見圖13。由圖13可見，環線剛度正負向對稱明顯；隨著位移的增大，各模型剛度退化模式和規律趨于一致，且在加載前期剛度退化較快，加載后期退化速率放緩；節點蓋板長度越大的模型初始剛度越大，這是因為翼緣連接板遠離節點核心區，塑性鉸外移距離加大。

3.2 柱軸壓比對抗震性能影響

柱軸壓比是影響抗震性能的一個重要因素，試驗的柱軸壓比n取值為0.15，考慮到實際工程中該比值會偏大，所以本文模擬了3種柱軸壓比值，分別為0.2，0.3和0.5，以此來研究柱軸壓比對該試件抗震性能的影響。

3.2.1 骨架曲線和特征點分析

不同柱軸壓比模擬的骨架曲線見圖14。4條骨架曲線在加載前期比較相近，隨著位移的增大，骨架曲線走向出現變化，柱軸壓比增大會使屈服位移提前，由表1可知，n=0.5模型比BASE模型提前5.16 mm，峰值荷載過后，軸壓比較大的骨架曲線下降更快，延性系數有所下降，這是因為軸壓比增加時軸力變大，混凝土截面壓應力和壓應變都增加，致使受壓區高度增加，截面的極限變形能力減小，最終導致延性降低，方林等[14]研究型鋼混凝土十字形異形柱時也驗證了這點；BASE模型相比于n=0.5模型等效黏滯阻尼系數從0.348增加到0.391，提高了12.4%，徐金俊等[15]研究型鋼混凝土柱也同樣證明了提高軸壓比能增加試件的耗能能力，這是因為隨著柱軸壓比值的增大，模型的屈服位移、峰值位移和破壞位移都會提前，鋼材的屈服程度更高，說明柱軸壓比的增大能顯著提高模型的耗能能力。

3.2.2 強度退化和剛度退化

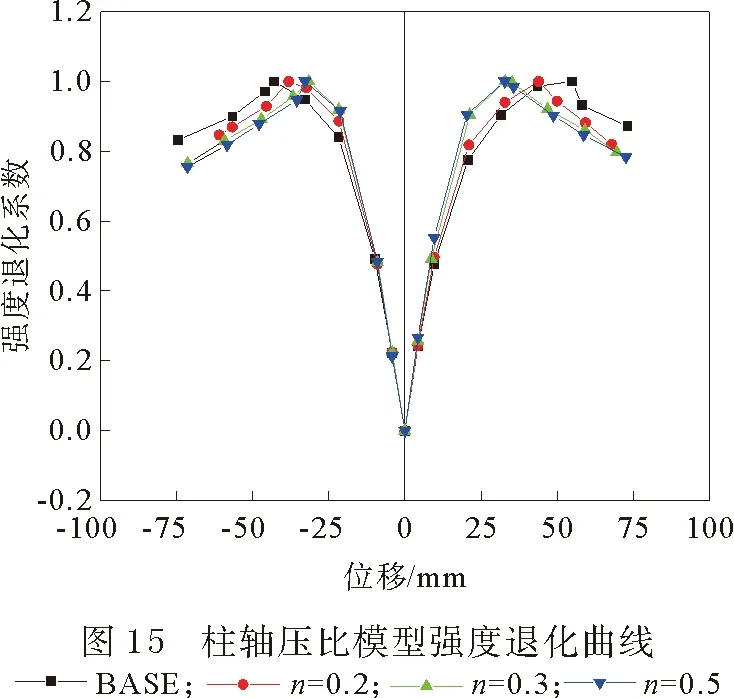
柱軸壓比的位移-強度退化系數曲線變化見圖15。可見，不同軸壓比的強度退化系數均在0.8～1之間區別較大；在加載前期，軸壓比較大的模型強度上升較快，屈服較早；各模型到達峰值點后，柱軸壓比越大曲線下降越陡峭，說明強度退化越快，模型的破壞也會提前，這也是導致高軸壓比延性較低的一個原因。

不同柱軸壓比下梁端位移和環線剛度曲線變化見圖16。軸壓比的增大對模型的初始剛度有著明顯的提升，這是因為上下混凝土柱和節點核心區之間隨著軸向壓力的增大而結合得更緊密；各模型環線剛度在加載前期整體呈線性退化，后期退化速率放緩，且加載到峰值荷載后，軸壓比越大的模型，退化速率越快。

4 結論

本文在擬靜力試驗的基礎上，通過ABAQUS對節點建立了8個精細化的有限元模型，研究了節點蓋板長度和柱軸壓比對預制裝配式SRC柱-H型鋼梁組合邊節點抗震性能的影響規律，得出結論如下：

1) 預制裝配式SRC柱-H型鋼梁組合邊節點在低周往復荷載作用下，其破壞位置均發生在翼緣連接板處，實現塑性鉸外移的目的，體現“強柱弱梁，強節點弱構件”的抗震設計思想。

2) ABAQUS有限元軟件模擬出的結果能夠較好地吻合試驗結果，說明有限元軟件模擬此類節點的抗震性能具有可行性，可為后續深入研究提供理論依據。

3) 節點蓋板長度所模擬5個模型的延性系數和等效黏滯阻尼系數平均值為2.63和0.33，體現出模型整體延性性能和耗能能力較好；當節點蓋板長度增加時，模型的破壞荷載和峰值荷載都有著顯著的提高，表明模型的承載能力得到提高，但模型的耗能能力、延性和滯回性能均有所下降。

4) 軸壓比從0.15增大到0.5，模型的屈服位移和破壞位移都會提前，耗能能力和初始剛度提升較為明顯，但加載后期強度、剛度退化速率也越快，延性下降較多。