基于“材料力學”課程教學的高階思維訓練案例設計
——以“預應力圓環熱驅自持續翻滾”為例
李 凱,杜長慎,柳軍修,余 勇,葛大麗
(安徽建筑大學土木工程學院,安徽合肥 230601)
0 引言
教育部自2019年起開始全面實施一流本科課程建設,一流課程(金課)建設引領著全國高校教育教學改革的發展方向.一流課程的主要特征概括為“兩性一度”,即高階性、創新性和挑戰度,其核心在于以“創新性”為方法,通過具有“挑戰度”的訓練,達到培養“高階性”思維的目的[1].培養高階性思維作為一流課程建設的首要目標,其不同于傳統的知識識記、理解和應用的培養目標.高階性思維培養目標要求學生通過對挑戰性問題進行獨立思考和深入探究,提出獨立個性化的見解和認識,以訓練形成創新性和批判性思維模式.高階性思維訓練案例是實現一流課程建設目標的重要途徑和關鍵環節.案例設計時,內容上應反映學科前沿性和時代性,難度上應具有一定挑戰度,形式上應能有效引導和激發學生思考、討論和探究,最終培養學生解決復雜問題的創新能力和高階性思維[2].
“材料力學”是土木、機電、材化和航空等多個工科專業的一門專業基礎課,對后續專業課的學習至關重要.材料力學作為獨立學科是以意大利科學家伽利略在1638年發表《關于力學和局部運動的兩門新科學的對話和數學證明》一書為標志,現已發展成為一門古老、經典且理論框架成熟的學科[3].傳統材料力學課程注重基本概念和公式推導,難以調動學生學習興趣并且容易束縛學生思維.近年在“材料力學”課程的講授內容、教學方法和考查手段等方面已有不少改革和創新,如實物演示[4]以及引入力學史[5]等.目前這些嘗試也已取得不少效果,但還需不斷探索以達到一流課程建設要求.
“材料力學”一流課程打造的關鍵在于圍繞“兩性一度”特征做好高階思維訓練的案例設計.力學及相關學科在近幾十年不斷涌現各種新成果,為培養學生創新意識與批判精神提供豐富優秀素材,可用于激發學生的學習興趣和探究熱情.為此本文選擇趣味性強、課程內容相關度高和具有一定挑戰度的“熱響應性預應力圓環自持續翻滾”問題[6]作為案例進行重構整合,從材料力學基本問題出發逐步推進到科學前沿問題,展示問題升階和啟發思考的高階思維訓練案例設計過程.
1 基本問題
本案例從材料力學中梁的彎曲基本問題出發進行設計[7].如圖1(a)所示,一根初始長度為L、橫截面半徑為R的圓柱細桿首先被純彎曲成圓環狀,接著細桿兩端面被相互粘結在一起,并形成一封閉圓環.此時,封閉圓環處于純彎曲狀態且其內部存在預應力.假設L>>R,細桿彎曲成圓環過程中材料變形較小,仍屬于彈性變形階段,不考慮屈服后塑性變形階段,圓環的拉壓彈性模量為E.細桿彎曲成圓環后,圓環橫截面上的環向應力和環向應變屬于拉壓應力和拉壓應變,不屬于切應變.求此預應力圓環橫截面上的環向拉壓應變及拉壓應力.

圖1 圓柱細桿被純彎曲為預應力圓環Fig.1 A thin cylindrical rod is purely bent into a prestressed torus
該基本問題涉及梁理論中的橫截面正應力計算.首先,截取半圓環進行受力分析,根據對稱性和平衡條件易得預應力圓環橫截面上的軸力為零.因此,預應力圓環軸線的周長等于細桿的初始長度L.設彎曲后圓環曲率半徑為Rp,則L=2πRp.在圓環橫截面內建立如圖1(b)所示的極坐標系,并進一步求解圓環橫截面任意位置(r,θ)處的環向拉壓應變.
把此預應力圓環分割成無數根環向纖維,環向纖維彎曲前的長度為細桿的長度L.細桿彎曲成圓環后,圓環橫截面(r,θ)處的環向纖維周長變為2π(Rp+rsinθ),如圖1(b)所示.根據拉壓應變定義,則環向拉壓應變可以計算為
(1)
注意到細桿長度與圓環曲率半徑之間的關系為L=2πRp,則公式(1)可進一步化簡為
(2)
從公式(2)可看出,圓環橫截面上環向拉壓應變隨角度周期性變化,且上下對稱.特別地,圓環橫截面上環向拉壓應變在內側區域為壓縮應變,在外側區域為拉伸應變.
利用梁理論中的單向受力假設,圓環橫截面上任意點處的環向拉壓應力與環向拉壓應變成正比.因此,環向拉壓應力可計算為
(3)
從公式(3)可看出,與環向拉壓應變對應,圓環橫截面上環向拉壓應力在內側區域為壓縮應力,在外側區域為拉伸應力.
2 進階問題一
在基本問題的基礎上,進一步進階求解此預應力圓環在給定非均勻溫度作用下的環向拉壓應力.如圖2所示,將上述預應力圓環置于一平面熱臺上,且圓環以角速度ω穩定翻轉.此時,在預應力圓環內會形成一非均勻溫度場,此非均勻溫度場由文獻[8]直接給出.求此時預應力圓環在非均勻溫度場下橫截面上的彎矩分量Mx.
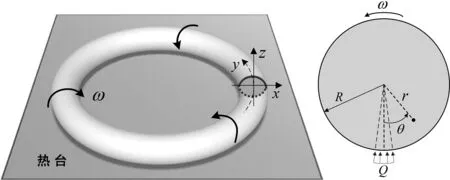
圖2 置于熱臺上的預應力圓環Fig.2 A prestressed torus placed on a hot surface
此題為熱力耦合問題,我們首先根據文獻給出的溫度場求解得到橫截面上的環向拉壓應變和拉壓應力,然后將環向拉壓應力對x軸取矩計算預應力圓環橫截面上的彎矩分量Mx.
2.1 預應力圓環橫截面的溫度場
預應力圓環在平面熱臺上穩定翻轉時,其內部的溫度場由文獻[8]直接給出,這里不進行詳細推導.計算內部溫度場時,假設預應力圓環與平面熱臺間接觸傳熱,且熱流量為Q.假設預應力圓環表面其余部分以熱對流的形式向空氣散熱,且不考慮流體力學中氣體流動的傳熱系數.計算溫度時,以環境溫度為參考溫度計算圓環內各點處的相對溫度,則圓環橫截面上的相對溫度分布可寫為[8]
(4)
式中的bern、bein分別為開爾文函數的實部和虛部,A0、An、Bn分別表示為
(5)
式中的h為傳熱系數,k為材料的熱傳導系數,D的表達式為
(6)

根據公式(4),圖3繪制了不同角速度下預應力圓環橫截面上的溫度分布.數值計算中,參數根據文獻中已有實驗選擇典型數值,分別為R=5×10-4m,Q=10×103W/m2,h=10 W/m2/oC,c=103J/kg/oC,k=0.1 W/m,ρ=103kg/m3和ω0=0.25/s[6].從圖3可見,圓環橫截面上的溫度場大小和分布受到翻轉角速度的明顯影響.一般地,翻轉角速度越大,圓環橫截面上溫度場的頂部與底部溫度差越小.

圖3 不同角速度時圓環橫截面上的溫度場Fig.3 Temperature fields on the cross section of a torus for different angular velocities
2.2 預應力圓環橫截面上的拉壓應變和拉壓應力
下面計算上述溫度場下預應力圓環橫截面上的環向拉壓應變和環向拉壓應力.熱應力問題是材料力學中的難點,準確理解總應變、熱應變和彈性應變三個重要概念是求解熱應力問題的關鍵.總應變一般由幾何條件可以直接確定,而熱應變與溫度相關.彈性應變為總應變與熱應變之差,且與彈性應力成線性關系.
由于預應力圓環橫截面上的溫度場是非均勻的,因此圓環受熱后其曲率半徑會發生變化.假設圓環受熱后其曲率半徑從Rp變為Rc,則環向總拉壓應變可類似于公式(2)由幾何條件計算為
(7)
從公式(7)可見,預應力圓環橫截面上的環向總拉壓應變仍隨角度周期性變化,且上下對稱,在內側區域為壓縮應變,在外側區域為拉伸應變.
假設預應力圓環受熱后,其橫截面上的拉壓熱應變與溫度成正比,則圓環橫截面內的拉壓熱應變可計算為
εT(r,θ)=CTT(r,θ)
(8)
其中CT為材料的熱膨脹系數.
由總應變等于熱應變與彈性應變之和,代入公式(7)和(8),拉壓彈性應變可計算為
(9)
進一步地,利用單向受力假設,預應力圓環受熱后其橫截面上的環向拉壓應力σ(r,θ)可計算為
(10)
從公式(10)可見,環向拉壓應力與橫截面上的溫度相關.
2.3 預應力圓環橫截面上的彎矩分量Mx
由公式(10)中已給出的環向拉壓應力分布可進一步計算橫截面上的彎矩分量Mx.根據材料力學梁彎曲理論,橫截面上的環向拉壓應力σ(r,θ)對x軸取矩并進行積分即得橫截面上的彎矩分量
(11)
聯立公式(2)、(4)-(11)可得Mx的解析形式為
(12)
從公式(12)可看出,橫截面上的彎矩分量Mx的大小與翻轉角速度相關.
3 進階問題二
下面,進一步進階求解預應力圓環的熱驅自持續翻轉問題.如圖4所示,將上述預應力圓環置于一平面熱臺上,圓環內部會形成非均勻溫度場,則其橫截面上彎曲力偶Mx能驅動預應力圓環發生自持續翻轉.假設預應力圓環穩定翻轉的角速度為ω,求圓環與熱臺之間的滑動摩擦系數.
此問題是個動力學平衡問題.首先求解施加在圓環微段兩端面上的彎曲力偶的合力偶,其是驅動圓環翻轉的驅動力.然后建立圓環穩定翻轉時驅動力與摩擦阻力之間的平衡方程,再根據已知的角速度反向推算圓環與熱臺之間的滑動摩擦系數.
3.1 預應力圓環穩定翻轉時的驅動力偶
選取預應力圓環微段dx為研究對象,圓環微段兩端橫截面上分別受彎曲力偶Mx作用,如圖4所示.注意到小曲率假設條件下,sin(α/2)≈α/2=dx/2Rc.則兩端面橫截面上的彎曲力偶的合力偶為兩端面力偶矢量Mx的矢量和,方向沿環向,大小可計算為
(13)
注意到M合作用在圓環微段dx上,則預應力圓環每單位長度上的驅動力偶可計算為
(14)
公式(14)表明,驅動力偶為橫截面上彎曲力偶Mx與圓環曲率之積.彎曲力偶Mx越大,驅動力偶越大.驅動力偶也隨曲率增加或曲率半徑減小而增加.
將公式(12)中的彎曲力偶Mx帶入公式(14),得到驅動力偶的解析形式為
(15)
從公式(15)可見,驅動力偶Md也與圓環的翻轉角速度相關.特別地,驅動力偶與膨脹系數和拉壓彈性模量成正比.這個結果意味著,提高膨脹系數和拉壓彈性模型是提升驅動力偶的重要途徑.
3.2 平衡方程及滑動摩擦系數
預應力圓環在穩定翻轉過程中,除了受到熱致驅動力偶的作用外,其還受到熱臺表面對其施加的滑動摩擦力.由于圓環處于動力學平衡狀態,可建立微段的平衡方程來求得滑動摩擦系數.首先取圓環的任意微段作為研究對象,由圓環微段重力為G=ρgπR2dx,故單位長度的圓環受到的滑動摩擦力大小可計算為[9]
Ff=CfρgπR2
(16)
其中,Cf為預應力圓環與平面熱臺間的滑動摩擦系數.
當圓環穩定翻轉時,圓環處于平衡狀態.選取單位長度圓環為研究對象,并對y軸建立力矩平衡方程,可得
Md=FfR
(17)
聯立公式(15)-(17)并化簡可得預應力圓環與平面熱臺之間的滑動摩擦系數為
(18)
值得注意的是,公式(18)中圓環曲率半徑Rc應受到滑動摩擦力和橫截面上非均勻溫度場的雙重影響,其可由圓環橫截面上的軸力條件進行確定.選取半圓環作為研究對象進行受力分析,根據半圓環在軸力與滑動摩擦力的共同作用下的平衡條件,易得軸力為FN=LCfρgπR2/2,則
(19)
將公式(10)中的環向拉壓應力代入(19)可得預應力圓環穩定翻轉時的曲率半徑為
(20)
公式(20)表明,預應力圓環在熱驅穩定翻轉時,其曲率半徑與受熱及滑動摩擦都相關.對于熱膨脹材料,受熱膨脹和滑動摩擦都導致圓環曲率半徑增大.
通過公式(18)和(20)進行數值計算,圖5繪制了預應力圓環熱驅穩定翻轉時的角速度與相應滑動摩擦系數間的依賴關系.計算中,參數根據文獻中已有實驗選取了典型數值,分別為R=5×10-4m,κ=20 m-1,CT=3×10-3/oC,E=10 MPa,ρ=103kg/m3,Q=3×103W/m2,k=0.1 W/m,h=5 W/m2/oC,ρ=103kg/m3和g=10 N/kg[6,10].從圖5可見,隨著預應力圓環翻轉角速度的增加,對應的滑動摩擦系數是單調減小的,此結果符合物理直覺.一般地,滑動摩擦系數減小,圓環穩定翻轉所需的驅動力偶也減小.又因驅動力偶隨著圓環翻轉角速度增大而減小.這樣,熱流不變的情況下,圓環可以獲得更大的翻轉角速度.
4 小結
本文以“預應力圓環熱驅自持續翻滾”問題為例,將現代力學前沿研究成果巧妙嫁接到“材料力學”課程教學中,通過遞進式、創新型和啟發性的案例設計方式,展示了高階思維訓練案例設計模式.此教學案例已被應用于“材料力學”示范課項目,初步成果表明可加強學生對書本原有基礎知識的理解,開闊學生的學術視野,以及培養他們的創新精神和批判意識.在教育教學改革探索實踐中,還可根據各學校及專業特點進行個性化設計,最終達成知識結構與能力兩方面的專業培養核心目標.

