多項式回歸的差分隱私保護算法

謝雅琪，楊 庚,2

(1.南京郵電大學 計算機學院，江蘇 南京 210046；2.江蘇省大數據安全與智能處理重點實驗室，江蘇 南京 210023)

0 引 言

多項式回歸是利用數理統計中的回歸分析，來確定兩種或兩種以上變量間相互依賴的非線性定量關系的一種統計分析方法，一般應用于數據屬性之間的關聯呈非線性的情況，擁有比線性回歸更加廣泛的應用場合，在數據挖掘領域中通常使用它對數據進行預測。

挖掘的數據集包含一些敏感屬性，在數據挖掘過程和數據發布中，如不加保護會引起隱私泄露[1]。在回歸分析中，常用的隱私保護算法有幾種類型：匿名算法、數據加密和數據擾動[2]等。匿名算法中，k-匿名算法使用較為廣泛；數據加密算法的研究中，常用的有同態加密[3]、安全多方計算[4]等；此外還有數據泛化[5]。

差分隱私(Differential Privacy，DP)[6]屬于數據擾動算法，它以數學理論為支撐，為數據的隱私保護提供了有力手段[7]。DP通過對數據集或者查詢函數添加噪聲等方式實現隱私保護。DP最為基礎的兩個機制為拉普拉斯機制和指數機制[8]，分別應用于查詢函數的輸出是數值型和非數值型的情況，該文涉及的機制都是拉普拉斯機制。

在面向回歸分析的差分隱私算法研究中，通常對數據集或查詢函數加噪聲。前者如Lei[9]提出的DPME算法，后者如函數擾動機制[10]。添加噪聲的過程中，可以選擇是否對代價函數進行敏感度分析。不做敏感度分析的情況下，可能會引入不必要的噪聲；如果進行敏感度分析，相較于前者，能夠減輕噪聲添加過量影響可用性的問題[11]，具有代表性的算法是Zhang等[12]提出的FM(Function Mechanism)，現在許多研究者都在研究基于FM的改進算法[13-16]。

1 相關工作

2006年，Dwork提出了差分隱私的定義，它通過對數據集或者模型添加噪聲實現隱私保護。相較于傳統的隱私保護算法，差分隱私不僅擁有數學理論作為支撐，而且能夠無視攻擊者所擁有的知識背景，提供了有力的隱私保護。目前，差分隱私的機制仍在逐步完善中[17-18]。在差分隱私保護算法被提出后，面向回歸分析領域的差分隱私算法研究在噪聲添加機制方面主要分為了兩類：直接對數據集添加噪聲和對查詢函數添加噪聲。

早期面向回歸分析領域的差分隱私研究集中在對數據集添加噪聲方面，如Lei的DPME算法[9]，但這些算法不對數據集進行分析，直接對數據添加噪聲，在數據集的維度較大時，會引入大量不必要的噪聲影響數據集的可用性。

2011年，Chaudhuri等[10]提出了一種對回歸模型的代價函數的系數添加噪聲的差分隱私保護算法，并且對代價函數的敏感度進行了分析，進一步減少了噪聲的添加量，提高了數據的可用性。在此基礎上，Zhang等[12]提出了函數機制FM，該算法進一步提高了訓練結果的精確性。Wang等[15]基于FM算法的思路，提出了DPC算法，主要為了應對模型逆向攻擊(Model Inversion Attack)[19]，提高數據的安全性。

該文的主要貢獻為：設計了三個面向多項式回歸的差分隱私算法，通過多組實驗衡量并比較它們在數據可用性方面的性能，并且優化了算法使其能用于高維度的數據集。

2 理論基礎

2.1 多項式回歸分析

多項式回歸分析是根據自變量與因變量的依賴關系進行建模的統計分析方法,通常在自變量和因變量呈非線性關系時使用，如圖1，是一個簡單一元二次多項式回歸的擬合結果，圖中點對應每條數據(x,y)。

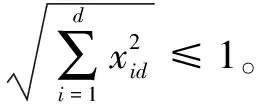
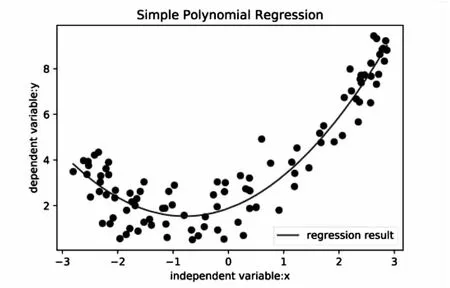
圖1 簡單多項式回歸的擬合結果

多項式回歸的擬合可以通過變量替換，將其轉換成多元線性回歸處理，通過如公式(2)的映射，將每個g(x)轉化為新的自變量zi，就可以得到多元線性回歸模型。

(1)

(2)

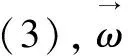
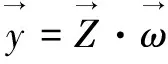
(3)

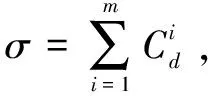
(4)

(5)

2.2 差分隱私保護技術

定義1(差分隱私[6])：當且僅當算法A的輸入為兩個鄰近數據集D1和D2(最多只有一條記錄有差別的兩個數據集)且滿足式(6)時，算法A滿足ε-差分隱私。

Pr[A(D1)∈0]≤eε·Pr[A(D2)∈0]

(6)

其中，ε是可以任意設置的隱私預算，Pr[A(D1)∈0]代表輸入為D1時，算法A的輸出屬于集合O的概率。

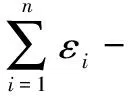
2.3 全局敏感度

定義2(全局敏感度)：假設有兩個鄰近數據集D和D',那么對于一個函數f：D→Rd，它的全局敏感度定義為：

(7)

3 面向多項式回歸分析的差分隱私保護機制

3.1 多項式回歸算法

(8)

再對式(8)利用最小二乘法求得ω*：

(9)

3.2 面向多項式回歸分析的差分隱私保護算法

3.2.1 面向多項式回歸的函數算法

面向多項式回歸的函數算法(Functional Mechanism on Polynomial Regression)簡稱FM-on-PR。

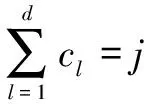
(10)

FM-on-PR對回歸模型的代價函數使用多項式逼近后轉化為多項式，如式(11)：

根據式(4)和式(11)，可以將fD(ω)簡化為fD(ω)=aω2+bω+c，對系數a,b,c各添加上服從Lap(Δf/)分布的噪聲，如式(12)所示：

(12)

全局敏感度的推導與計算過程如下：

對于鄰近數據集D和D'，以及它們的代價函數fD(ω)和fD'(ω)：

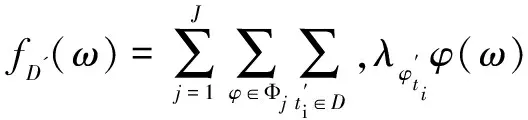
根據全局敏感度的定義(見定義2)有：

由此，可以得到全局敏感度Δ為：

(13)

算法1：FM-on-PR。

輸入：數據集D，隱私預算，代價函數fD(ω)；

2：for each 1≤j≤Jdo

3： for eachφ∈Φjdo

5： end for

6：end for

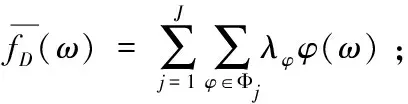
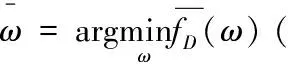
由2.1節可知，因為多項式回歸可以通過變量替換轉為多元線性回歸進行訓練，因此任意多項式回歸的代價函數最終都可以表示為式(4)的多元線性回歸形式。

此外，根據推導，全局敏感度的公式(13)表明其只與數據集的維度有關，與代價函數是否為線性并無關系。因此全局敏感度的計算公式同樣適用于轉換為多元線性回歸之后的多項式回歸。由此達成了使用FM算法的前提條件，后續的幾個算法同理。

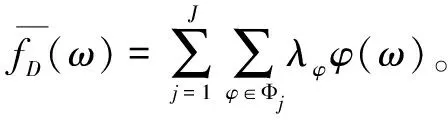
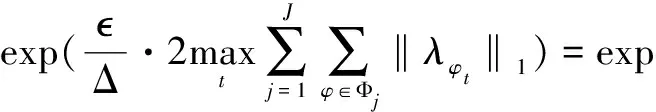
3.2.2 面向多項式回歸的不同系數擾動函數算法

面向多項式回歸的不同系數擾動函數算法(Functional Mechanism with Different Perturbation of Coefficients on Polynomial Regression)簡稱DPC-on-PR。

定義Xs是包含了所有會泄露隱私的敏感屬性xs的集合。在FM算法的基礎上(見3.2.1)，對φ也進行劃分：只要φ中有包含了任何一個Xs中的元素對應的系數ωs，就將其納入集合Φs，否則納入Φn中。對于Φs中的φ項，分給其相對較少隱私預算s， 而分給Φn的隱私預算n則相對更多。設s=γn，其中0<γ<1。給代價函數添加完噪聲后，只需對添加過噪聲的代價函數進行最優化求解，算法流程如下：

算法2：DPC-on-PR。

輸入：數據集D，隱私預算，代價函數fD(ω)，隱私預算比率γ；

1：設置Φs={}，Φn={};

2：for each 1≤j≤Jdo

3： for eachφ∈Φjdo

4：ifφ不包括任意屬于敏感集Xs中元素的ωs

5：then將φ添加至集合Φn；

6：else將φ添加至集合Φs；

7： end if

8： end for

9：end for

10：計算全局敏感度Δ(算法同(13))；

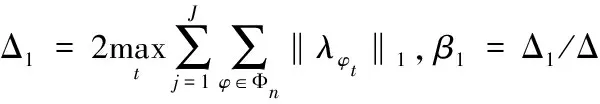
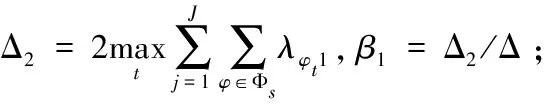
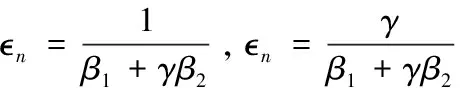
14：for each 1≤j≤Jdo

15： for eachφ∈Φjdo

16： ifφ∈Φnthen

18： else

20： end if

21： end for

22：end for

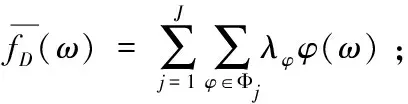
首先可以算出：

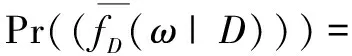
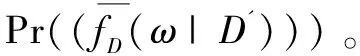
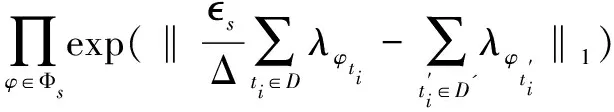
證畢。

3.2.3 面向多項式回歸的差分隱私預算分配算法

面向多項式回歸的差分隱私預算分配算法(Differentiated Privacy Budget Allocation on Polynomial Regression)簡稱DPBA-on-PR。

根據式(13)，可以得到代價函數fD(ω)的全局敏感度為ΔfD(ω)=2(2d+d2)。

隨后，將fD(ω)(fD(ω)的表達式同式(4)形式)拆解開為2個單項式，分別為：

根據式(13)，同理可得gD(ω)和hD(ω)的全局敏感度分別為ΔgD(ω)=2d2,ΔhD(ω)=4d。

可以發現整個多項式的全局敏感度和兩個單項式的全局敏感度滿足如下關系：

ΔfD(ω)=2(2d+d2)=ΔgD(ω)+ΔhD(ω)

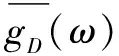
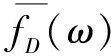
算法3：DPBA-on-PR。

輸入：數據集D，隱私預算，代價函數fD(ω)；

1：計算gD(ω)的全局敏感度Δf1，hD(ω)的全局敏感度Δf2；

2：設gD(ω)的系數是a，hD(ω)的系數是b；

3：if Δf1>Δf2then

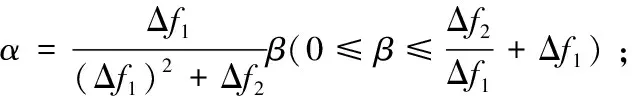
5：else

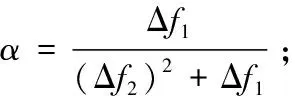
7：end if

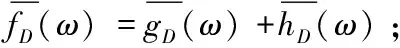
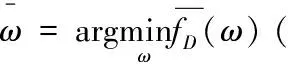
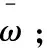
算法流程中的參數β，是用來調節gD(ω)和hD(ω)的隱私預算分配比率的變量，其取值范圍的端點(見上述算法流程中步驟4)分別對應著將總的隱私預算全部分配給gD(ω)和全部分配給hD(ω)。顯然，gD(ω)相對于hD(ω)自然有較高的全局敏感度(式(13))，因此必須合理制定β的取值使得gD(ω)添加噪聲規模較小。

在高維度的數據集中，根據全局敏感度的計算方法(式(13))，gD(ω)的全局敏感度Δf1更是遠遠高于Δf2的，因此為了保證訓練結果的準確性，gD(ω)應該被分配到更多的隱私預算使得對其添加的噪聲規模降低，根據算法3流程中的步驟4，β的取值就要增大。

表1總結了β為各個取值時，gD(ω)和hD(ω)被分配到的噪聲服從的分布。

表1 β的取值以及gD(ω)和hD(ω)的噪聲分布

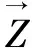
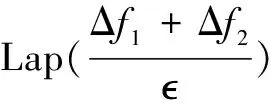
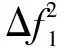
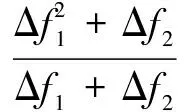
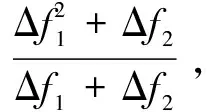
(14)

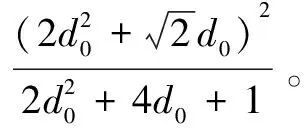
最終β的取值范圍為：

證明：如果給gD(ω)，hD(ω)分別分配隱私預算g，h，且設=h+g。根據FM機制中的相關證明(定理2)，這三個單獨的代價函數又分別滿足g-差分隱私，h-差分隱私。于是，由定理1差分隱私的串行組合性可知，ΔfD(ω)的算法滿足-差分隱私。

4 實驗與分析

4.1 實驗環境

實驗環境為Intel(R) Core(TM) i7-9750H CPU 2.60 GHz,16G內存。實驗使用的數據集為：來自UCI的聯合循環發電廠(CCPP)數據集、個人家庭用電(IHEPC)數據集和Kaggle上獲取的diamond鉆石價格預測數據集。屬性如表2所示。

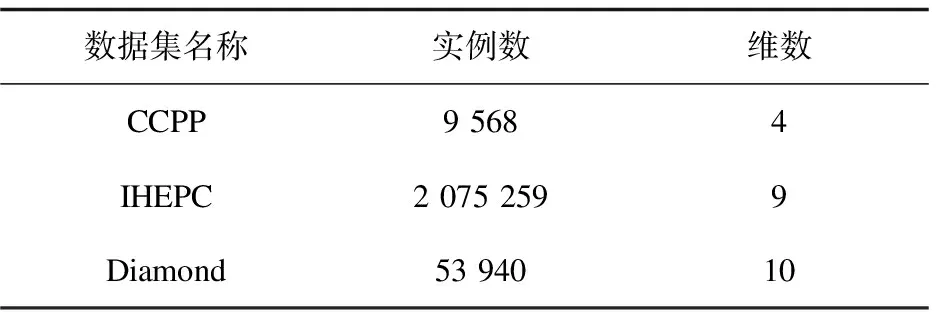
表2 實驗中使用的數據集

為了驗證所設計算法的可行性，在這三個數據集上依次使用該算法進行訓練，通過訓練結果的精確度來判斷它們的可用性。此外，為了檢測隱私預算對模型準確性的影響，對每個數據集也將以不同的隱私預算進行多次訓練。由于噪聲的影響，也會進行多次實驗取結果的均值。

4.2 實驗結果及其分析

4.2.1 隱私預算對擬合結果準確度的影響

回歸分析有多種性能指標衡量其精確性，該文使用擬合優度(R2)來衡量訓練模型的準確性，R2的取值不會超過1，越接近1表示訓練結果的準確度越高，特別地，當R2<0時，表示擬合結果尚不如取數據集的平均值的精度高。

在多項式回歸的階數設置方面，經測試，對于CCPP數據集，將它們的階數設置為3最佳；對于IHEPC數據集和Diamond數據集，設置為2最佳。

從圖2可見，三個數據集的訓練結果均遵循隱私預算越大，訓練出的模型精確度越高的規律，并且當隱私預算足夠大時，幾個算法之間的精確度差距甚微，同時與無隱私保護的算法的精確度接近。

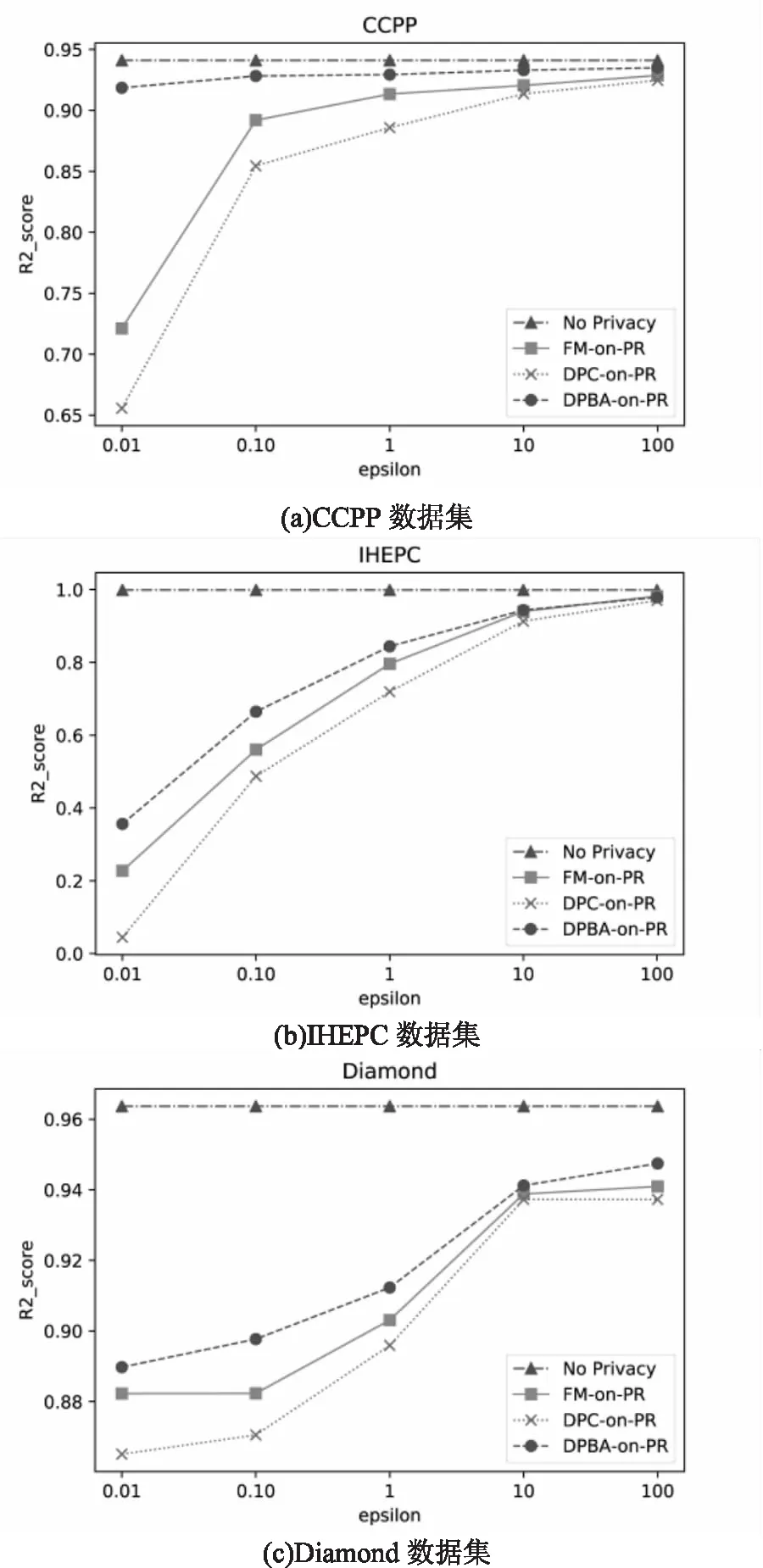
圖2 在不同隱私預算下對三個數據集進行回歸訓練的結果

另一方面，無論基于哪個數據集的實驗，結果都表明DPBA-on-PR算法擁有最高的精確度，其次是FM-on-PR算法，DPC-on-PR算法最次。由于DPC-on-PR算法提出的目的是為了加強FM-on-PR算法的數據安全性，它只對會泄露隱私的特征變量添加更多噪聲，并考慮每個特征變量與輸出的關聯性，因此可能會對高敏感度的特征變量添加很多不必要的噪聲，從而大大降低訓練結果的準確性，因此精確性方面不如FM-on-PR算法。

4.2.2 DPBA-on-PR算法中β取值對訓練精確度的影響

因為對該算法中隱私預算分配策略的優化是針對高維度的數據集，所以這部分實驗中，選取維度較高的diamond數據集進行實驗，經過數據集預處理后，它的原始維度d為9，將其多項式形式的目標函數轉換為多元線性回歸之后的維度d0達到了54。同樣，衡量準確性的標準仍然是擬合優度R2。

圖3是DPBA-on-PR算法取不同β值并在不同隱私預算下的訓練結果，橫坐標epsilon是隱私預算的取值，縱坐標是擬合優度R2；標簽為value1的曲線中β取值均為value1=Δf1(即式(14)中的不等式上限)，在本實驗中具體取值為5 832(計算公式參考表2)；標簽為value2的曲線中的β取值為即式(14)中的不等式的中間項以及得出的β取值新上限)，在本實驗中具體取值為5 771；標簽為value3的曲線中的β的取值為即式(14)中的不等式下限)，在本實驗中具體取值為5 621。

由于value1與value2的R2_score(即縱坐標值)差值和value2與value3的差值相差過大不便于比較，因此將比較結果分在了兩張圖表中。

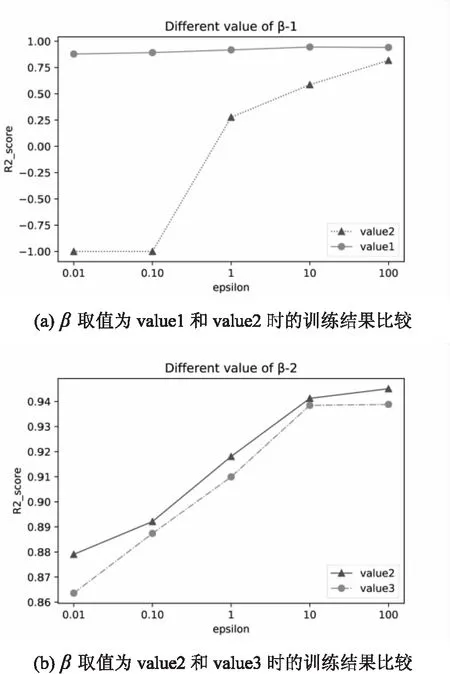
圖3 DPBA-on-PR算法中β取值對準確性的影響

圖3(a)中，β取值為value1時，在=0.01和0.1的情況下，實驗得到的R2_score均遠遠小于-1，而在此圖中，value1代表的曲線在這兩個取值上均以-1代替表示，僅代表在這兩種情況下，訓練結果不理想。結果看來，β取值為value2的訓練精確度比value1時高很多，尤其在隱私預算較小時更明顯。

圖3(b)中，β取值為value3時，如3.2.3小節所述，此時的DPBA-on-PR算法就與FM-on-PR算法一致，β取值為value2的訓練精確度比取值為value3時高，結合4.2.1的實驗，這也證明了DPBA-on-PR算法的精確度性能是優于FM-on-DPBA的。

綜上，在3.2.3節中β的取值策略是可行的。

5 結束語

該文研究并設計了三個面向多項式回歸的差分隱私保護算法，并且理論證明了它們滿足差分隱私性質；三個算法與無隱私保護的多項式算法的訓練結果進行的比較，也證明了它們的可用性；此外經實驗，得出了數據可用性最高的算法為DPBA-on-PR的結論。由于DPC-on-PR和DPBA-on-PR分別在數據安全性和數據可用性方面進行了改進，因此在實際應用中，可以根據需求來對兩個算法進行選擇。總體來說，面向多項式回歸分析的差分隱私算法研究的重點是數據的安全性和可用性間平衡的問題，通常這方面研究的切入點是隱私預算的分配與全局敏感度的計算，目前，全局敏感度的計算也并沒有達到相當精確的程度，因此，噪聲的添加量仍有優化的余地，這也將是未來面向多項式回歸的差分隱私保護算法研究的方向。