再入飛行彈道解析計算方法研究

朱恒偉，肖 振，曹晶瑩，楊 丁

（空間物理重點實驗室，北京，100076）

0 引 言

從20 世紀50 年代起，科研人員就開始了對于滑翔彈道解析解的研究。在定升阻比的條件下，Chapman給出了再入彈道的近似解析解；在此基礎上，Loh放寬約束條件，得到了升阻比變化條件下的再入彈道近似解析解；Vinh 等則給出了定升阻比平衡滑翔縱向彈道解析解；Bell將問題擴展到三維，分析了定升阻比和定傾側角條件下的平衡滑翔三維彈道解析解。隨著預測校正制導技術的發展，研究重點轉向了高精度的縱向彈道解析。郭興玲等提出用包含地球旋轉效應的常滑翔角飛行段近似實際滑翔飛行軌跡的方法，并基于該方法推導得到了長航時縱向遠程滑翔飛行軌跡近似解；李邦杰等則給出了平衡滑翔最大升阻比條件下的高度、彈道傾角、飛行時間和射程的解析解；徐明亮等在準平衡滑翔條件下，假設速度傾角是常值，得到了航程、高度和速度傾角三者之間的解析關系式；Yu 等通過給定縱向升阻比和橫向升阻比關于能量的表達式，推導得到了準平衡滑翔軌跡的縱程、橫程和速度傾角的解析解；胡錦川等將彈道分段，并將升力系數分解為橫向分量、平衡滑翔縱向分量和平穩滑翔縱向分量3 部分，以此為基礎推導得到了滑翔軌跡的解析解。

本文重點針對高速飛行器平衡滑翔階段的彈道工程估算問題，推導出高速飛行器再入飛行的解析解。以滑翔彈道簡化方程為基礎，分別采用攝動法求解高度和彈道傾角的數值解，數值積分法求解航程與飛行時間的數值解，同倫分析法求解擬緯度和航向角的數值解，由此得到平衡滑翔階段彈道的近似解。

1 彈道方程的簡化

高速飛行器處于平衡滑翔階段時，其彈道傾角及其變化率滿足如下條件：

在高速再入的初期，飛行高度很高，彈道傾角很小，一般不能滿足相容初始條件。如果飛行高度過低，在只能利用向上的升力時也難以滿足相容初始條件（雖然可利用負升力維持平衡，但此時飛行器所承受的熱載荷很大，不能長時間維持）。對于初始條件不可能相容的情況，都要經過特殊的拉平段飛行，使飛行器達到平衡滑翔的初始狀態（稱為彈道拉平），然后才能進行平衡滑翔飛行。

2 主要解析解推導

2.1 高度和彈道傾角的解

當忽略式（11）中關于的二次項時，就等于將式（10）右端所含直接變為的結果。

從物候期觀測結果分析，各類月季均能正常發芽、開花、結果，在未采取冬季防凍、旱的情況下，除冷香玫瑰外，其余各品種均不能正常越冬，在西寧地區引種栽培均需采取防凍、旱措施。

由式（6）可得：

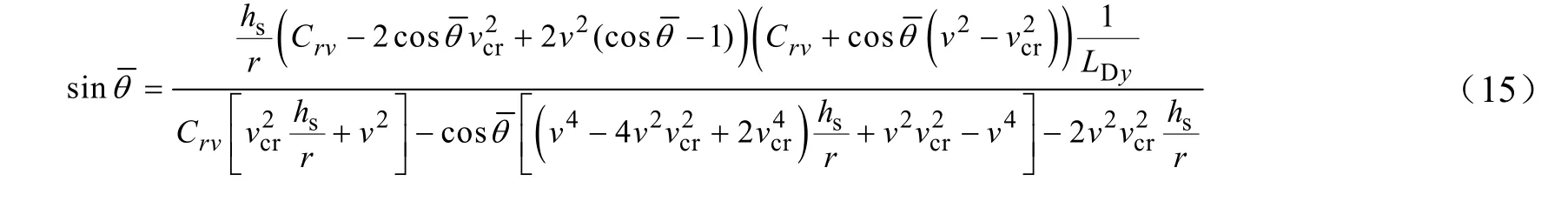
2.2 航程的解

由式（2）的第2 式、第4 式可得：

其實，內鄉縣衙大堂上還掛著一副對聯：“欺人如欺天毋自欺也，負民即負國何忍負之。”建議當代官員們多念叨幾遍這副對聯，多照照鏡子。沒有民，哪有官，你給誰當官？官待民要不“欺”不“負”，要愛要畏，否則，為官者羞見內鄉縣衙的對聯！

3 仿真分析

對滑翔飛行器的剩余航程進行估計，所得結果如圖2 所示。

圖1 某滑翔飛行器三維彈道（示例1）Fig.1 The Three-dimensional Trajectory of Glide Vehicle(Exampe 1)

圖2 剩余航程估計及估計誤差（示例一）Fig.2 The Estimation and Its Error of Remaining Range(Exampe 1)

某滑翔飛行器示例2 的三維彈道如圖3 所示，仿真中采用最大升阻比約為3.2 的某型滑翔飛行器的飛行數據，滑翔飛行器終端速度=1800 m/s，分別使用式（20）所示方法和工程中常用的零階解方法對滑翔飛行器的剩余航程進行估計，所得結果如圖4所示。

圖3 某滑翔飛行器三維彈道（示例2）Fig.3 The Three-dimensional Trajectory of Glide Vehicle(Exampe 2)

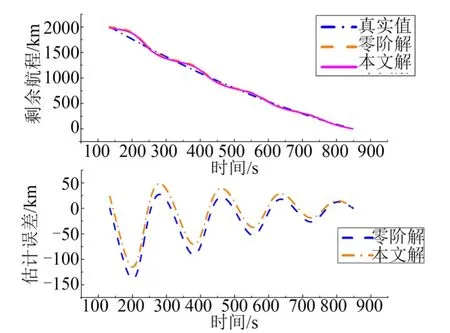
圖4 剩余航程估計及估計誤差（示例2）Fig.4 The Estimation and Its Error of Remaining Range(Exampe 2)

由仿真結果可看出，本文方法相比零階解方法估計精度高，能夠對零階解方法估值略高的不足進行補償，但本文方法求解的過程稍微繁瑣，兩種方法在具體的工程應用中需根據實際問題的需求進行選擇。

4 結束語

滑翔飛行器解析解的研究能夠為滑翔飛行特性的理論研究、基于解析解的軌跡生成和制導方法提供基礎，本文針對平衡滑翔階段的剩余航程估計問題進行了近似解的推導，所得結果能夠實現對剩余航程更高精度的估計。