車載跟瞄轉(zhuǎn)臺的擾動補償控制技術(shù)研究

吳忠明 ，張立中 ，白楊楊 ，孟立新 ，張樂儀

（1.長春理工大學(xué) 機電工程學(xué)院，長春 130022；2.長春理工大學(xué) 空地激光通信國防重點實驗室，長春 130022）

車載光電跟瞄轉(zhuǎn)臺應(yīng)用于空間激光通信，主要進行目標(biāo)的捕獲、跟蹤和瞄準(zhǔn)，完成載體間的通信［1-2］。在復(fù)雜的車載環(huán)境下，轉(zhuǎn)臺受到車輛姿態(tài)變化、路面振動沖擊、外界風(fēng)載擾動、自身不平衡力矩以及摩擦力矩等擾動力矩的影響［3］。為了保證車載跟瞄轉(zhuǎn)臺可以對運動目標(biāo)進行高精度穩(wěn)定跟蹤，就要求控制系統(tǒng)具有很強的擾動抑制能力。傳統(tǒng)的線性PID控制已難以滿足高精度穩(wěn)定跟蹤的要求［4］，因此，可以從控制算法的角度，采用一些擾動補償控制方法。

目前，在光電跟蹤系統(tǒng)中對擾動補償方法應(yīng)用的越來越多，文獻［5］將自抗擾控制［6］用于望遠(yuǎn)鏡光電跟蹤系統(tǒng)的速度環(huán)，以補償和抑制跟蹤系統(tǒng)存在的摩擦等非線性問題，改善了系統(tǒng)的速度控制性能；文獻［7］將前饋控制應(yīng)用于艦載平臺，將擾動量的一階導(dǎo)數(shù)作為速度前饋，進行補償，系統(tǒng)的跟蹤精度提高了一個數(shù)量級；文獻［8］將干擾觀測器應(yīng)用于三軸轉(zhuǎn)臺，用以補償外部擾動力矩的影響，平臺速度誤差得到提高。

本文在傳統(tǒng)的PID控制基礎(chǔ)上，將速率陀螺測得載體姿態(tài)變化的角速度加入到速度環(huán)輸入端，進行可測擾動的前饋補償，再將自抗擾控制中的擴張狀態(tài)觀測器加入到位置環(huán)控制器，通過PI+ESO控制實現(xiàn)對轉(zhuǎn)臺位置和外部未知擾動的實時觀測和補償，提高系統(tǒng)的抗干擾特性，進而提高系統(tǒng)的跟蹤精度。通過在MATLAB中對跟瞄轉(zhuǎn)臺方位軸系統(tǒng)（包含驅(qū)動器、電機以及機械負(fù)載）進行仿真測試補償方法的效果，最后在車載跟瞄轉(zhuǎn)臺控制系統(tǒng)中進行跟蹤性能測試，驗證算法的有效性。

1 伺服系統(tǒng)組成及原理

搭建方位軸的開環(huán)控制系統(tǒng)：直流力矩電機、SA57驅(qū)動器、23位增量式光柵編碼器、CCD可見光相機、單軸光纖速率陀螺。進行轉(zhuǎn)臺方位軸開環(huán)頻率測試，輸入頻率連續(xù)變化的正弦掃頻信號，通過ARM+FPGA處理器實時讀取方位電機編碼器位置信息，上位機連接控制器采集數(shù)據(jù)，并將數(shù)據(jù)保存后進行處理，通過相關(guān)分析法［9］得到采樣數(shù)據(jù)的幅頻和相頻曲線，建立直流力矩電機模型，采用自適應(yīng)差分進化算法［10］辨識控制系統(tǒng)的傳遞函數(shù)模型，最后根據(jù)傳遞函數(shù)模型進行控制器設(shè)計，完成仿真分析和實驗測試，其不考慮高頻段辨識的轉(zhuǎn)臺方位軸傳遞函數(shù)為：

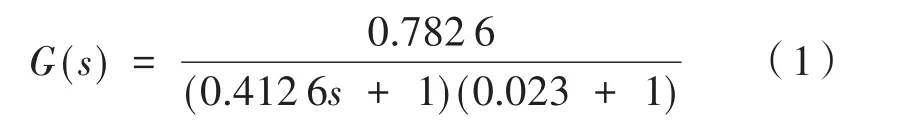
其伺服系統(tǒng)組成如圖1所示。

圖1 伺服系統(tǒng)組成

2 陀螺速度前饋

前饋控制的原理就是使系統(tǒng)多一個前饋通道，被測得的已知擾動可以通過前饋控制器改變控制量。利用擾動附加的控制量與擾動量影響的疊加消除或減少干擾的影響。

根據(jù)前饋控制的特點，將車載跟瞄轉(zhuǎn)臺方位軸和俯仰軸的速率陀螺測得的車體振動速度作為干擾源，前饋到速度環(huán)輸入端，陀螺速度所對應(yīng)的車體振動、搖擺作為位置環(huán)輸入端的輸入量，這樣通過前饋控制補償可以達(dá)到隔離車體振動的作用。圖2為前饋控制原理框圖，圖3為傳遞函數(shù)簡化框圖。

圖2 前饋控制原理框圖

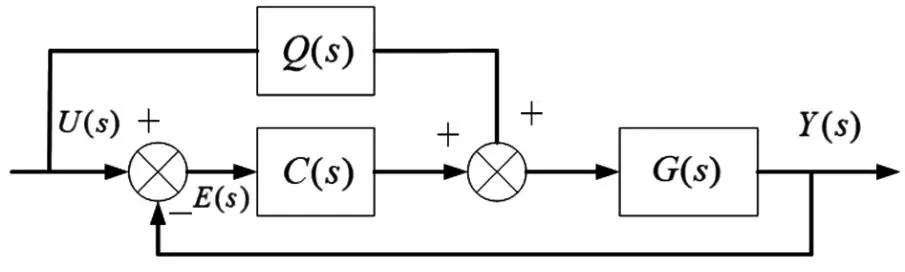
圖3 傳遞函數(shù)簡化框圖

圖3中，U(s)是位置變化量輸入，E(s)是誤差信息，C(s)是位置環(huán)控制器，G(s)是速度閉環(huán)傳遞函數(shù)。可得系統(tǒng)的傳遞函數(shù)和誤差控制函數(shù)為：

由此可以看出，只要讓式的分子為零，則可以控制誤差為零，得：

G(s)為速度閉環(huán)傳遞函數(shù)，可以簡化為一階小慣性環(huán)節(jié)為：

其中，K是閉環(huán)增益；Tv是速度閉環(huán)經(jīng)過等效后的時間常數(shù)，可得：

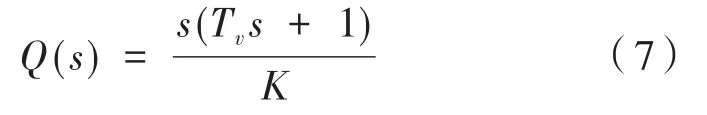
可以看出Q(s)為輸入信號一階、二階或更高階的導(dǎo)數(shù)所構(gòu)成。由此可將車體振動搖擺信息作為輸入，速率陀螺測得速度量作為速度前饋輸入到速度環(huán)控制器，達(dá)到隔離車體振動帶來的已知擾動。

采用單軸速率陀螺測量在車體實際振動條件下陀螺的速度輸出，并用上位機采集一定時間數(shù)據(jù)，根據(jù)采集的數(shù)據(jù)在MATLAB中進行有無前饋控制的仿真，分為以下兩種情況：

（1）將采集到的陀螺速度值進行積分處理，作為位置環(huán)的位置輸入，然后將速度值前饋到速度環(huán)輸入端，得到位置跟蹤誤差；

（2）將采集到的陀螺速度值進行積分處理，只作為位置環(huán)的位置輸入，不進行前饋控制的補償，得到位置跟蹤誤差。

圖4、圖5分別為有無陀螺速度前饋的跟蹤誤差，對比兩次仿真中的跟蹤精度。采用前饋控制，誤差最大值為0.013 77°，均方差0.003 439°（1σ），不采用前饋控制誤差最大值0.048 95°，均方差0.015 81°（1σ）。可得速度前饋有一定的隔離車體振動的效果。

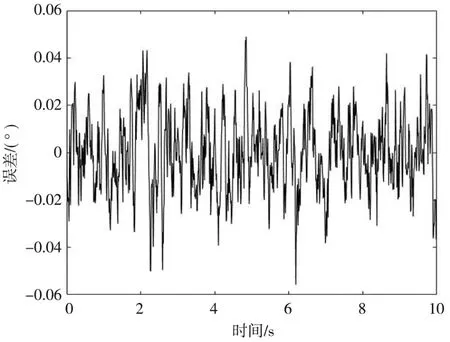
圖4 無速度前饋跟蹤誤差

圖5 有速度前饋跟蹤誤差

3 設(shè)計擴張狀態(tài)觀測器

3.1 擴張狀態(tài)觀測器

擴張狀態(tài)觀測器是自抗擾控制技術(shù)［5］的核心部分，它將控制系統(tǒng)的內(nèi)部擾動以及外部擾動當(dāng)成一個未知的狀態(tài)變量，進而得到一個新的狀態(tài)觀測器，由于擴張了一個新的狀態(tài)變量，所以稱為擴張狀態(tài)觀測器。擴張狀態(tài)觀測器不需要對擾動進行測量，也不需要系統(tǒng)本身有關(guān)擾動的任何先驗知識，只需要根據(jù)系統(tǒng)輸入信號以及輸出信號數(shù)據(jù)，就能夠?qū)崟r估計系統(tǒng)狀態(tài)以及擴張的擾動。因此，擴張狀態(tài)觀測器得到了廣泛使用。擴張狀態(tài)觀測器（ESO）可以對系統(tǒng)的未知擾動進行預(yù)測和跟蹤，通過多級變換，可以將系統(tǒng)轉(zhuǎn)化為積分結(jié)構(gòu)應(yīng)用于傳統(tǒng)PI控制。

3.2 基于位置環(huán)的ESO

ESO的核心思想將跟瞄轉(zhuǎn)臺經(jīng)過光柵編碼器取得的位置信息中的未知擾動經(jīng)過擴張狀態(tài)觀測器，可以實現(xiàn)對跟瞄轉(zhuǎn)臺的位置環(huán)、速度內(nèi)環(huán)和不確定變量進行預(yù)測和補償，進而通過調(diào)節(jié)參數(shù)，提高跟蹤精度。其中位置環(huán)的ESO框圖如圖6所示。

圖6 位置環(huán)ESO框圖

速度環(huán)控制器設(shè)計的主要目的是保證系統(tǒng)的帶寬和相位裕度滿足要求，采用超前滯后校正設(shè)計速度環(huán)控制器，在低頻段，速度閉環(huán)傳遞函數(shù)可近似等效為一階慣性環(huán)節(jié)，考慮到編碼器的傳遞函數(shù)可等效為積分環(huán)節(jié)，位置環(huán)被控對象可以表示為：

將其轉(zhuǎn)換為狀態(tài)方程為：

其中，x1為位置測得量；1為位置求導(dǎo)，即速度值；x2為速度測得量；u為擴張狀態(tài)觀測器控制量；d為轉(zhuǎn)臺未知擾動。利用光柵位置量設(shè)計擴張觀測器，以實現(xiàn)對狀態(tài)觀測器的準(zhǔn)確估計。將作為被擴張的轉(zhuǎn)態(tài)變量x3，即，其導(dǎo)數(shù)為m(t)，令，則系統(tǒng)可擴展為一個新系統(tǒng)：

新系統(tǒng)中，擴張狀態(tài)觀測器通過轉(zhuǎn)臺輸出響應(yīng)和設(shè)計的控制量，可以對系統(tǒng)狀態(tài)變量進行估計，進而設(shè)計三階擴張狀態(tài)觀測器，對速度、位置和未知擾動進行觀測補償，如下：

其中，z1、z2、z3為位置、速度和不確定因素的估計值；y為被控對象輸出，即編碼器采集位置量；β1、β2、β3為觀測器的增益。令e1=z1-y=z1-x1，e2=z2-x2，e3=z3-x3，可得誤差方程為：

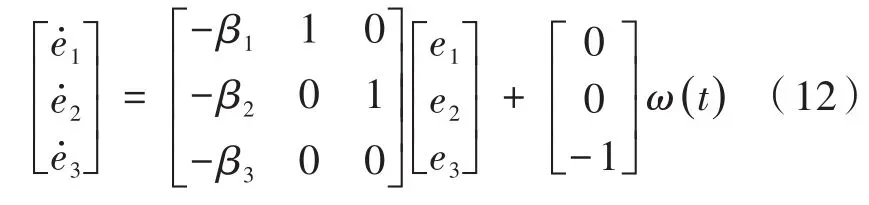
可以看出擴張狀態(tài)觀測器是一個有著兩項輸入三項輸出的系統(tǒng)，為了可以很好地抑制干擾，引入觀測器帶寬ω0，而且β1、β2、β3滿足如下關(guān)系，特征方程表示為：

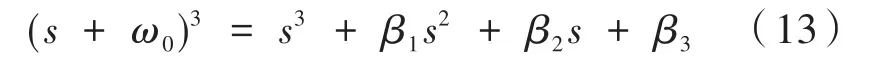
其中，ω0為設(shè)計觀測器控制帶寬。ω0的選取值越大，對狀態(tài)變量的估計越準(zhǔn)確，一般情況下ESO適應(yīng)范圍較寬，參數(shù)較容易整定，但系統(tǒng)噪聲增大，所以應(yīng)根據(jù)實際進行選擇。根據(jù)帶寬需要就可以確定線性 ESO 的參數(shù)，將位置環(huán)控制器輸出設(shè)置為u0，將擴張狀態(tài)變量估計值z3作為一個反饋值，進而可以對系統(tǒng)控制量進行修正，可以設(shè)計帶動態(tài)補償?shù)淖饔檬剑缦拢?/p>

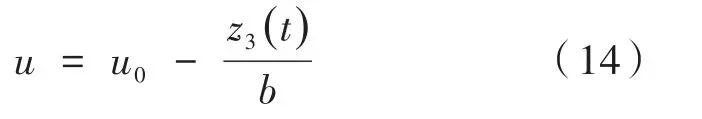
其中，b可以看作是控制量的放大倍數(shù)。則校正后系統(tǒng)可寫為：

可見校正后系統(tǒng)是一個連續(xù)積分串聯(lián)型系統(tǒng)，可以根據(jù)z3的控制律對系統(tǒng)進行動態(tài)補償，通過上面兩式可以得到：

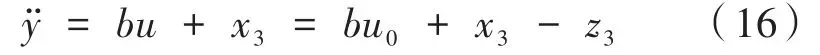
式中，x3近似等于z3。ESO的幾個參數(shù)需要合理選擇，進而可以得出z3的觀測值，從而對位置環(huán)控制器的輸出進行修正，系統(tǒng)可以轉(zhuǎn)換為一個積分式：

由于微分環(huán)節(jié)對系統(tǒng)噪聲較敏感，因此根據(jù)上式設(shè)計位置環(huán)的PI控制器為：

通過選擇PI控制器的KP,Ki，根據(jù)轉(zhuǎn)臺輸出量，并將其作為反饋量，不斷進行輸出量的反饋，在擴張狀態(tài)觀測器下對系統(tǒng)的未知擾動進行補償，用補償后的控制量重新設(shè)計傳遞函數(shù)，從而位置環(huán)PI控制器的傳遞函數(shù)可以寫為：

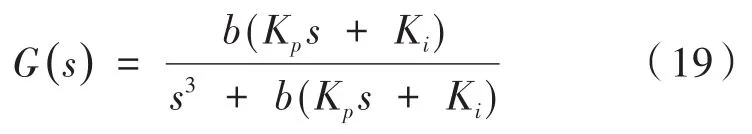
通過上述設(shè)計的控制器，以公式（1）的傳遞函數(shù)模型為例在MATLAB的Simulink中建立ESO的仿真模型，如圖7所示。經(jīng)過速度環(huán)的閉環(huán)控制后，進行帶有擴張狀態(tài)觀測器的位置環(huán)控制。

圖7 ESO仿真框圖

在PI控制器參數(shù)Kp、Ki，系統(tǒng)增益b一定的情況下，給定跟瞄轉(zhuǎn)臺最大角速度10°/s，角加速度 10 °/s2的等效正弦θ=10sin(t)°，得到ω0=5、10、20、40、70帶寬下的正弦跟蹤誤差曲線和局部放大曲線如圖8、圖9所示。

圖8 正弦跟蹤誤差

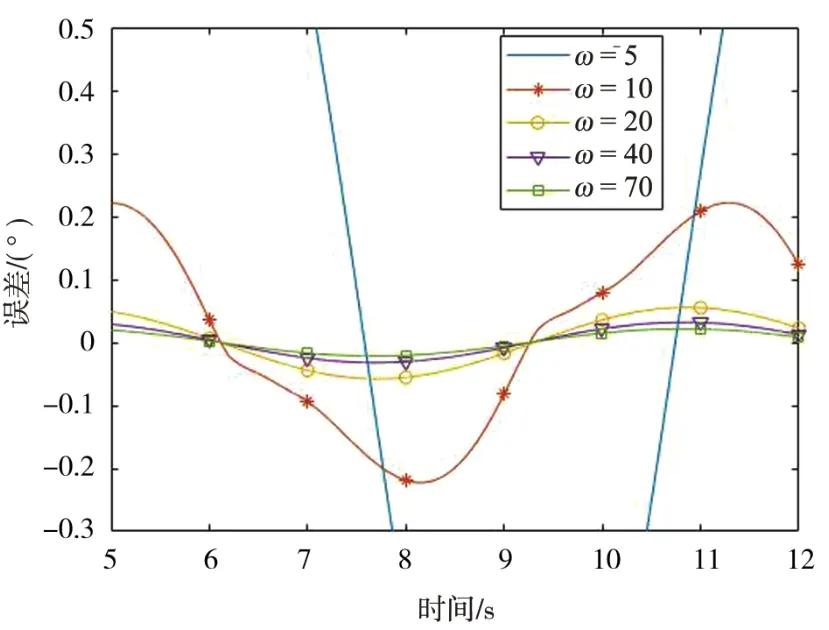
圖9 跟蹤誤差局部放大圖

可以看出隨著觀測器帶寬ω0的增大，正弦跟蹤穩(wěn)定后最大誤差由1.1°減少到了0.002 114°，跟蹤精度逐漸提高，由擴張狀態(tài)觀測器原理可知，隨著ω0的增大，估計值z3對系統(tǒng)不確定擾動的估計值越準(zhǔn)確，進而提高系統(tǒng)跟蹤精度。但是也可以看出跟蹤初期調(diào)節(jié)時間逐漸增大，因此，對不同帶寬進行階躍響應(yīng)分析，不同帶寬下階躍響應(yīng)曲線和閉環(huán)頻率特性曲線如圖10、圖11所示。

圖10 階躍響應(yīng)曲線

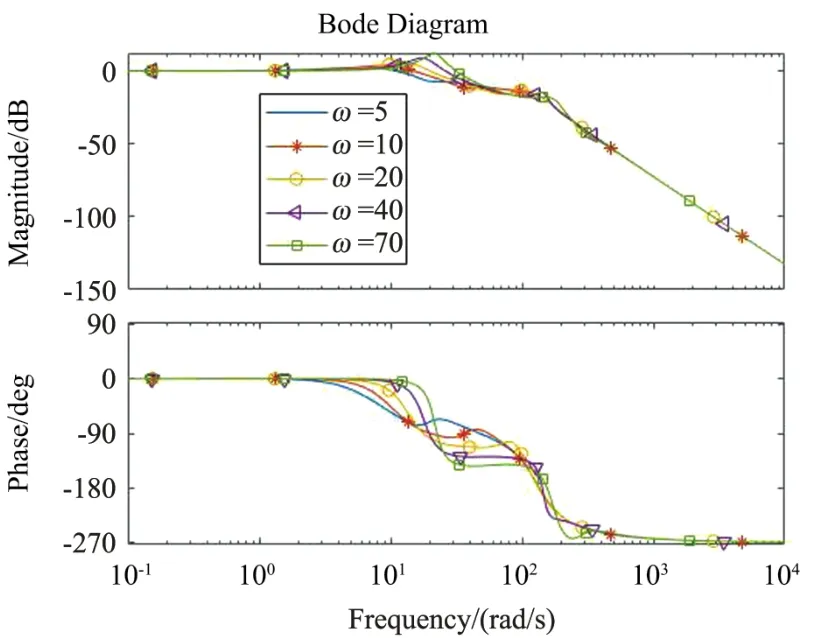
圖11 幅頻和相頻曲線

可以看出在觀測器帶寬ω0=5時，系統(tǒng)超調(diào)量小，但是調(diào)節(jié)時間過長，從ω0=10開始，隨著觀測器帶寬增大，系統(tǒng)超調(diào)量不斷增大，調(diào)節(jié)時間越來越長，逐漸產(chǎn)生震蕩，由于加入觀測器不斷補償，導(dǎo)致相位裕度逐漸減小，使動態(tài)性能下降，調(diào)節(jié)時間增大。

經(jīng)過上述對帶有擴張狀態(tài)觀測的位置環(huán)閉環(huán)系統(tǒng)分析，最后選擇觀測器帶寬ω0=20，b=100，Kp=28.59，Ki=169.45，對帶有 ESO 的位置環(huán)PI控制和不帶ESO的閉環(huán)控制進行有干擾信號的跟蹤精度測試，進一步證實ESO對外界干擾的抑制效果和補償能力比只有PI控制下好。

進行有干擾的仿真實驗，在理想輸入階躍響應(yīng)1°情況下，在第3 s施加幅值為10°，寬度為1 s的階躍干擾。如圖12為PI和PI+ESO對干擾的抑制效果。傳統(tǒng)PI下，最大波動誤差為0.54°，而增加了ESO后，波動誤差降低為0.215°，說明ESO對階躍干擾力矩有一定的抑制效果。

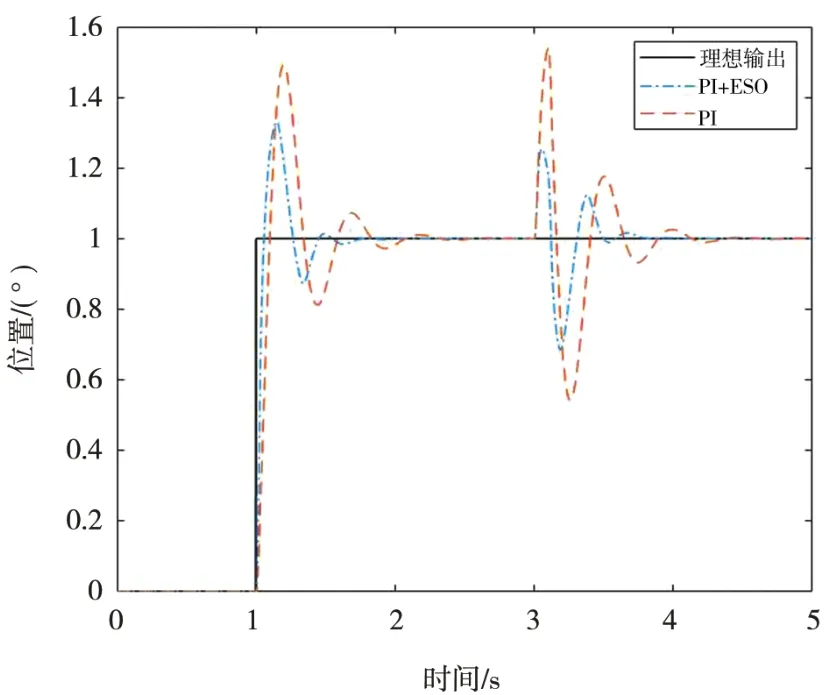
圖12 階躍干擾曲線

同樣在相同的階躍輸入下，同時初始施加最大角速度10°/s，角加速度10°/s2的等效正弦θ=10sin(t)°干擾，圖13為PI和PI+ESO對干擾的抑制效果。傳統(tǒng)PI下，波動最大誤差為0.058°，而增加了ESO后，波動最大降低為0.003°，說明ESO對正弦干擾力矩有較好的抑制效果。

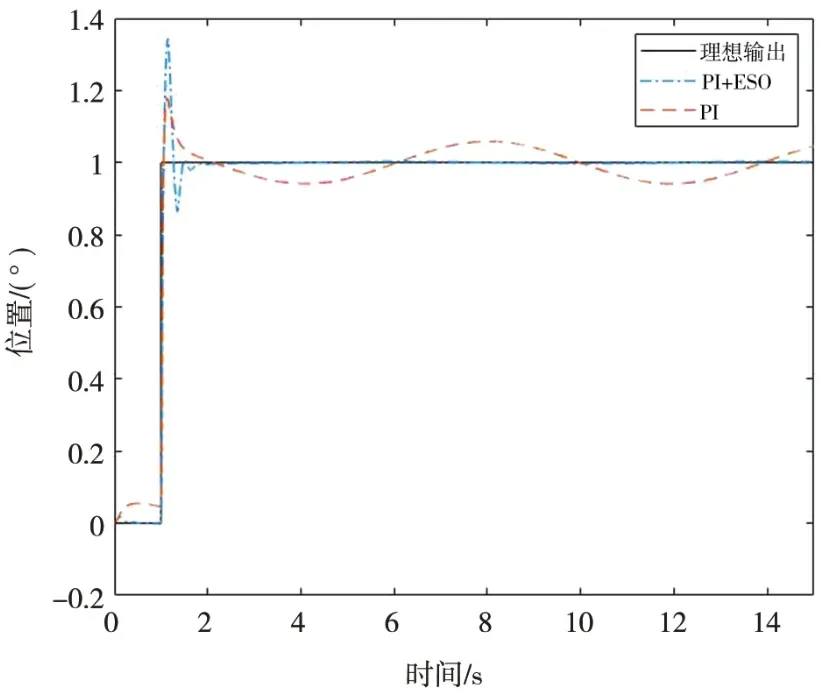
圖13 階躍下正弦干擾曲線

對系統(tǒng)輸入1°/s，模擬目標(biāo)勻速運動，同時輸入同等幅值和頻率的正弦干擾，模擬車載姿態(tài)運動，圖14是正弦干擾下的對比曲線。傳統(tǒng)PI控制下，穩(wěn)定后最大誤差為0.104 5°，而增加了觀測器ESO后，最大誤差降低為0.005 386°，跟蹤精度提高了19.4倍，說明ESO對正弦跟蹤下正弦干擾力矩有較好的抑制效果。

圖14 勻速跟蹤下正弦干擾跟蹤誤差

4 實驗研究

為測試陀螺速度前饋、PI+ESO在實際車載光電平臺上的抗干擾效果和跟蹤精度，對實際車載光電跟瞄轉(zhuǎn)臺進行測試驗證。圖15為實驗測試場景，在搖擺臺上對車載跟瞄轉(zhuǎn)臺的方位軸進行測試，對轉(zhuǎn)臺進行最大角速度10°/s，角加速度10°/s2的等效正弦引導(dǎo)測試，PI和PI+ESO誤差對比曲線如圖16所示，設(shè)置搖擺臺方位按最大角速度10°/s，角加速度10°/s2的擾動作正弦擺動，對遠(yuǎn)處速度為1°/s勻速運動的平行光管發(fā)出的信標(biāo)光進行跟蹤，誤差對比如圖17所示。

圖15 實驗測試平臺

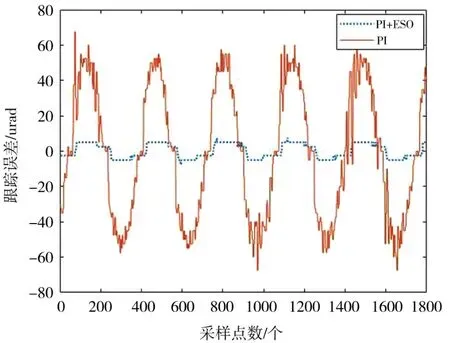
圖16 等效正弦引導(dǎo)誤差

圖17 正弦擾動下跟蹤誤差

在等效正弦引導(dǎo)測試下，應(yīng)用傳統(tǒng)PI的控制算法，轉(zhuǎn)臺的正弦引導(dǎo)均方誤差為37.33 μrad（1σ），PI+ESO 下的均方誤差為 4.13 μrad（1σ），在有擾動的正弦跟蹤下，PI控制下轉(zhuǎn)臺的跟蹤均方誤差為111.5 μrad（1σ），PI+ESO下的均方誤差為 11.64 μrad（1σ），可以確定引入前饋控制和擴張狀態(tài)觀測器能有效估計和克服平臺的擾動并進行補償。

5 結(jié)論

本文針對車載光電平臺高精度穩(wěn)定跟蹤問題，采用擾動補償控制算法，將速率陀螺測得角速度前饋到速度環(huán)輸入端，通過前饋控制實現(xiàn)對可測擾動的補償，同時在位置環(huán)引用擴張狀態(tài)觀測（ESO），實現(xiàn)對轉(zhuǎn)臺位置和未知擾動的實時觀測和補償，并在MATLAB中分別采用PI控制算法和PI+ESO的控制算法，進行Simulink仿真分析，仿真結(jié)果證實了速度前饋補償和PI+ESO的算法具有更小的跟蹤誤差，在搖擺臺上對轉(zhuǎn)臺進行最大角速度10°/s，角加速度10°/s2的正弦干擾跟蹤測試中，PI+ESO下的跟蹤均方誤差為11.64 μrad（1σ），跟蹤精度相比 PI控制提高 9.58倍。證實了前饋控制和PI+ESO控制算法對抑制擾動和補償?shù)挠行浴?/p>