基于模態特性分析的方向盤擺振研究

胡賦鑫，閆炳旭，張策

（中國礦業大學（北京）機電與信息工程學院，北京 100083）

0 引言

隨著技術的發展，人們對駕駛舒適度的要求日益提高，車輛的NVH性能已經成為評價車輛舒適性的重要指標之一，方向盤作為駕駛員的手部直接接觸的部位，其振動大小是汽車NVH品質的重要因素。某公司生產的某款皮卡車型，接市場反饋，當車速達到80 km/h以上時，方向盤出現擺振現象。車輛在行駛過程中，轉向系統不但承擔著轉向作用，還承擔著從路面-輪胎傳遞來的振動，這對汽車的操作穩定性、安全性產生了一定的負面影響，嚴重時甚至會引起安全事故。在行駛過程中，由于制造精度問題，或者是零部件本身性能造成的一些難以避免的問題還是會存在，這些問題無法根除，只能是通過一定的方法來減弱，從而降低其對行駛過程中的不利影響[1-3]。

本文通過使用CATIA對轉向系統進行整體三維建模并對其進行適當的簡化，在ABAQUS中對轉向系統進行模態特性研究以得到其振型以及固有頻率，分析方向盤振動的類型。通過合理的優化和建議來改善該問題。

1 有限元模型建立

本文以某皮卡車轉向系統為研究對象，該車型具體數據如表1所示。

表1 車輛參數

根據相關參數信息，利用三維建模軟件CATIA建立轉向系統模型，如圖1所示。

圖1 轉向系統三維模型

在完成建模之后，需要導入ABAQUS軟件中，此過程需要轉換為中間格式，此次轉換的為CATIA V4格式。導入有限元分析軟件的裝配體圖，如圖2所示。

圖2 簡化后的有限元模型

對有限元模型進行前處理，主要包括定義材料屬性（如表2）、網格劃分、定義接觸面、定義邊界條件、定義分析步、裝配、設置歷程輸出及場輸出。

表2 有限元模型材料

有限元前處理中網格布置種子越多，劃分的就會越細致，計算結果也就越準確。但是當網格密度增加1.方向盤2.轉向管柱3、5.萬向節4.轉向傳動軸6.左橫拉桿7.轉向機8.直拉桿9.右橫拉桿到某個程度后，網格數量的增多對計算結果的精度幾乎無影響，但使得計算時間大大增加。所以需要確定最優網格數量。進行網格無關性檢驗，使用3種不同尺寸的網格。根據模型尺寸，最終確定為：第一種采用自適應網格劃分，第二種和第三種在全局網格尺寸設置中，使用倍數變化的方式，分別在第一種網格尺寸的基礎上增大1.4倍和縮小1.4倍。

為節省計算時間，只求3種情況的一階固有頻率，對比結果如圖3所示。可知，不同的網格尺寸，得到的固有頻率有一定的差異，從數值上看，網格尺寸越大，得到的固有頻率越低，因為較粗的網格對結構的細節忽略得越多。再將網格尺寸減小1.4倍后，此時網格數量為744 086個，得到的1階固有頻率為10.33 Hz，說明上述網格模型已基本收斂。故采用自適應網格來進行后續分析，此時網格數量為531 490個。最終得轉向系統有限元模型網格劃分如圖4所示。

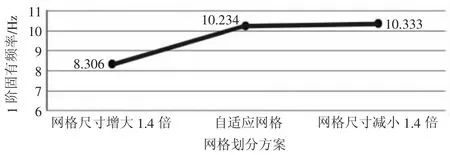
圖3 網格無關性驗證曲線

圖4 轉向系統有限元模型網格劃分效果圖

2 轉向系統的模態分析

2.1 模態分析理論

模態分析的目的是確定其系統特性的固有頻率和振型等模態參數。確定振動源，并在設計過程中將激勵的頻率范圍與轉向系統某階次振型不發生重合[4]。如果在設計過程中轉向系統設計得不合理，導致汽車內部共振，則滿足不了NVH的性能要求。

轉向系統的振動會造成和車內其它機構的共振，并且使駕駛員感受到不舒適。因此必須了解其模態參數，在充分考慮其受到的慣性力、阻尼力及剛度因素后[5]，轉向系統的振動微分方程可以表示為

式中：M為質量矩陣；C為阻尼矩陣；K為剛度矩陣；x為質點位移。

并引入下式：

式中：x=[x1,x1… xn]T為幾何坐標（質點處位移）；φ為模態矩陣（振型矩陣）；q=[q1,q2… qn]T為模態坐標。

則將式（2）代入式（1）可得模態解耦方程:

其中，第r階模態為

式中：ξn為第r階模態的阻尼比；Mr、Kr、Cr為模態質量、剛度和阻尼，其中Fr=φTrf。

由式（4）可得，第r階模態坐標為

其特征方程為Kr－ω2Mr+jωCr=0；特征值為λ1，2=σr±jωr。式中：σr為阻尼因子；ωr為第r階固有頻率。

2.2 ABAQUS模態分析過程

本次研究的模態分析的主要步驟：建立三維模型，導入ABAQUS中，并對其進行網格劃分，進行裝配、定義約束、定義分析步，定義邊界條件，求解器選擇Lanczos。最終在上述步驟設置完畢后提交作業等待計算結果。其中邊界條件的設置要模擬轉向系統在整車中裝配的實際情況去設定，從而進行約束模態的求解。

根據實際情況分析得，將轉向系統的支架與儀表橫梁相連的位置約束6 個自由度，如圖5所示。轉向機殼體與車身相連的地方約束6個自由度，如圖6所示。

圖5 轉向支架約束設置

圖6 轉向機殼體約束設置

對于傳動軸與轉向機接觸（萬向節）的地方施加約束，約束其3個平移方向的自由度，如圖7所示。

圖7 萬向節約束設置

定義連接方式：連接方式的模擬，在轉向系統結構上常采用的連接方式有螺接和焊接。針對不同的分析目的，對連接方式的模擬是不同的。本次研究對轉向橫拉桿與齒條的球頭連接采用球鉸連接。由于系統的局部運動不是本次的研究重點，所以采用tie連接的約束方式。轉向系統整體的約束如圖8所示。

圖8 轉向系統約束及連接設置

對轉向系統進行模態分析，在分析步中設置step-1為“線性攝動頻率”，特征值的提取方法選擇Lanczos（蘭索斯）求解器，特征值的提取個數定義為10，創建并提交作業進行計算。當工作狀態變為已完成時，進入后處理模塊查看最終分析結果，可得前10階的模態振型。

2.3 模態分析結果

在振型提取過程中，只選取方向盤發生變化的階次。可得方向盤變化的前6階模態如圖9～圖14所示，模態振型頻率值及振型分別如表3所示。

圖9 轉向系統1階模態

圖10 轉向系統2階模態

圖11 轉向系統3階模態

圖12 轉向系統4階模態

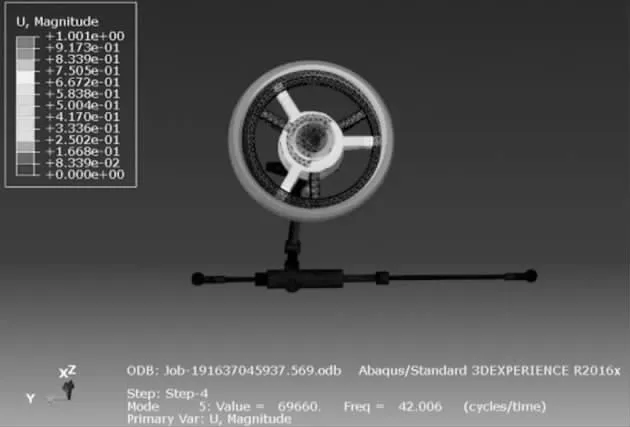
圖13 轉向系統5階模態

圖14 轉向系統6階模態

通過振型圖（圖9～圖18）可以看出方向盤的主要變型還是以繞著轉向管柱為主，在3階模態之前，是在全局坐標系下，水平面內的以X軸方向、Y軸方向及Y軸切向方向發生旋轉所表現的方向盤變形。而在3階模態之后出現整體水平面內的2階彎曲，并隨著階數的增加，扭轉變形越劇烈，且固有頻率隨著階數增加而增加。由表3可知，方向盤的低階頻率主要在10～50 Hz范圍內。當方向盤的固有頻率小于其所受的激勵頻率時，會發生共振現象。

圖15 轉向系統7階模態

圖16 轉向系統8階模態

圖17 轉向系統9階模態

圖18 轉向系統10階模態

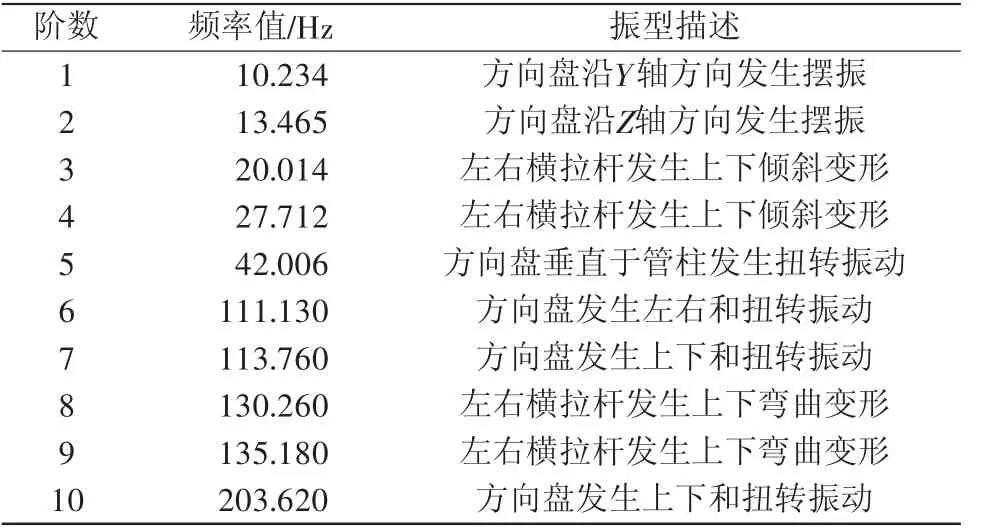
表3 方向盤各階模態頻率

從方向盤振動機理來分析可知，方向盤振動與其產生共振的途徑主要為兩種：路面-輪胎引起的激勵以及發動機激勵。從路面-輪胎角度分析得，在高速行駛中，路況良好瀝青路面上行駛時，路面激勵頻率為1～2 Hz。與方向盤1階頻率無重合。故推測方向盤一階固有頻率和車輪1階激勵存在直接聯系：本文研究對象使用的輪胎型號是175/65 R14，行駛速度范圍在60～100 km/h，該型號輪胎的車速與輪胎1階激勵的關系如表4所示，在該行駛范圍內，輪胎的第1階頻率為8.04～13.4 Hz。方向盤的1階固有頻率為10.234 Hz，80 km/h時車輪的1階激勵為10.72 Hz，兩者相差4.7%，且車輪1階激勵大于方向盤的1階固有頻率。故分析可得，在行駛過程中，輪胎的不平衡激勵是引起方向盤振動的主要原因。

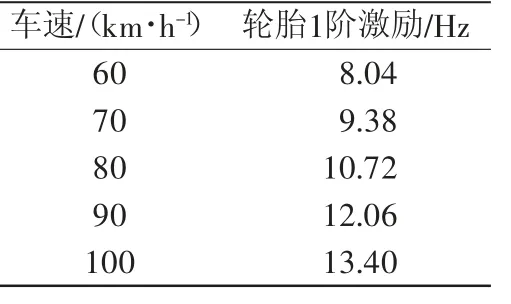
表4 車速與輪胎1階不平衡激勵的關系

從發動機角度分析得：首先需要計算汽車發動機所產生的激勵，來判斷是否與方向盤產生共振，發動機激勵為

式中：f為發動機激勵頻率；n為發動機轉速；m為發動機缸數的一半。

本課題皮卡安裝的是直列4缸、四沖程發動機。皮卡發動機怠速的轉速為750 r/min，經過計算，發動機怠速下頻率為25 Hz，高于第2階模態頻率（13.456 Hz），低于第3階模態頻率（42.006 Hz）。根據車輛設計要求，各系統的頻率要避開發動機怠速激勵3 Hz以上。因此該車型在此情況下基本不會發生共振。在皮卡正常運行車速下，發動機的轉速通常在1400～2000 r/min，經過計算，發動機正常運轉時，頻率為46.67～70.00 Hz。這個范圍與方向盤發生變形的頻率范圍都不重合。所以針對于該款車型來說，方向盤的振動不是由發動機引起的。

綜上分析得，確定車輪轉動時的1階不平衡激勵引起了方向盤的振動。車輪的1階不平衡激勵是由其本身不平衡量導致的，而車輪的不平衡量是制造時難以徹底消除的問題。對于解決方向盤振動可以有如下幾種解決方法：1）通過修改結構參數來使固有頻率與激勵頻率解耦，其中包括懸架控制臂的襯套剛度及懸架減振器阻尼系數、輪胎的剛度及阻尼系數等。2）對轉向管柱支架的結構外形尺寸做改進（如增加厚度等）來提高結構剛度。3）改變輪心到主銷的距離，輪心到主銷的距離影響著車輪總成對主銷產生的力矩，如果該值越小，那么車輪總成繞主銷的轉動慣量就越小，即振動響應也越小。但由于改變了該值，會導致整個懸架的硬點發生改變，上下控制臂、輪轂、制動盤等零部件需要重新開發，故這個方法在實際中并不采用[6]。4）增加轉向盤外圈質量，增大其轉動慣量，減小方向盤振動響應。

3 結論

本文針對客戶的反饋“在80 km/h時，某型皮卡車的方向盤發生擺振”的現象來進行分析。使用CATIA對某型皮卡車的轉向系統進行建模，并使用ABAQUS對其進行約束模態分析，在考慮轉向系統實際的裝配情況以及表面接觸和平移約束的情況下，分析得到了方向盤的6階振型以及固有頻率。在確定激勵源時，排除了發動機激勵，通過車速與車輪轉速的關系分析，得到引起方向盤擺振的原因是車輪在高速旋轉時的1階不平衡激勵，從而與方向盤產生共振，進而使得在車輛行駛過程中具有一定的危險，因此需要對其進行結構或者零件參數上的改進。本文利用模態分析分析方向盤擺振問題，在一定程度上為改善汽車NVH性能，提高車輛安全性、振動穩定性提供了理論依據。