基于CATIA的輕型載貨汽車地面線的制作方法

熊燕，何瑞光

（安徽江淮汽車集團股份有限公司輕型商用車研究院，合肥 230000）

0 引言

隨著市場汽車更新迭代速度的加快，各主機廠對汽車開發周期也在不斷精簡壓縮，在車輛開發過程中充分利用CAD模擬整車實際情況對設計進行全面檢查和校核對提高開發效率至關重要。在汽車設計過程中整車最小離地間隙、縱向通過角、接近角、離去角等均需通過地面線測量其具體設計值，保險杠及前后側防護離地高度、視鏡離地高度、視鏡法規視野范圍、燈具離地高度等法規要求項也需通過地面線對各部件的位置進行合理布置，因此在設計過程中通過CAD軟件制作出與實際相符度較高的地面線對整車相關部件的布置具有極高的指導意義。

本文所述輕型卡車地面線是將車架視為參照物、地面相對車架的位置，對于同一車輛，由于懸架弧高、輪胎半徑會隨載荷的不同發生變化，因此不同載荷狀態下地面與車架的相對位置也不一樣。本文利用輕型卡車地面線制作原理，運用CATIA中的參數和公式工具，在CATIA中建立輕型卡車地面線制作的模型，在模型中可根據設計的需要改動制作地面線所需的相關參數的數值，從而得出不同整車、不同狀態下的地面線，能極大地提高設計效率。

1 地面線制作原理

本文中所涉及的整車坐標系及坐標軸與常規車輛設計相同[1]。地面線即為前輪和后輪下方的公切線，兩個公切點近似為輪胎Z方向最下方點。輪胎最下方點由2個因素決定：輪胎在一定負荷狀態下的半徑和輪胎中心坐標。輪胎中心坐標需通過前橋、板簧的位置、板簧在不同載荷狀態下的弧高進行推算得到。

前懸和前橋的裝配示意圖如圖1所示，板簧前包耳中心點與后包耳中心點的連線為該懸架的弦，其中前包耳中心點的位置不動，而后包耳中心點會隨著前懸架載荷變化繞吊耳中心點以半徑R進行圓周運動，因此弦的位置也是會發生變動的；弦到懸架最上端板簧的上平面的距離H為懸架的弧高，會隨著懸架載荷的變化發生變動；懸架各板簧及中間墊片的總厚度為d，h為前橋輪轂中心到前橋和板簧接觸面的垂直距離。

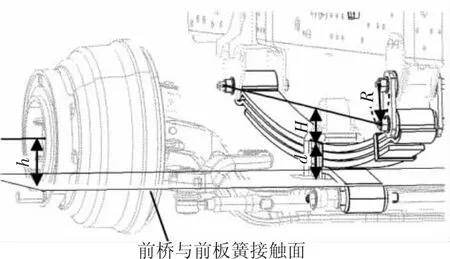
圖1 前懸和前橋裝配示意圖

由以上所述可知，當懸架弦的位置確定后，弦中心點Z坐標減去H、減去d、加上h即可得到前輪中心的Z坐標，前輪中心的Z坐標減去輪胎在一定載荷狀態下的半徑即為前輪接觸的地面處的Z坐標。后輪與地面接觸處的Z坐標計算原理與前輪大同小異，在后文中有詳細論述。根據前后輪與地面接觸處的Z坐標便可形成地面線。

2 參數公式建立

2.1 整車載荷及軸荷

在整車設計初期，首先確定的參數有：整車空載狀態的設計總質量G、空載前輪總負荷F1、空載后輪總負荷F2、整車軸距L、貨箱內長中心點到前輪中心線距離L0、滿載狀態下設計總質量G′。滿載狀態下駕駛室內乘坐人數為核載人數[2]，乘員體重按65 kg/人核算。上述參數中G=F1+F2，F1和F2的值與實際越相符，理論地面線與實際地面線也越相符。

滿載狀態下的前后軸荷值可通過力矩原理計算出來。如圖2所示，設定空載狀態下整車質心到前輪中心的水平距離為L1，貨箱的載荷為G0，滿載狀態下前后輪的負荷為F1′和F2′。

圖2 輕型載貨汽車受力示意圖

在空載狀態下，

在滿載狀態下，

其中，

將式（1）和式（3）代入到式（2）中得到

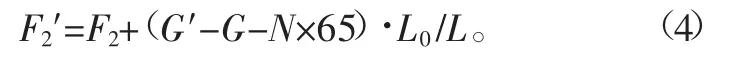
而

在CATIA中輸入設計已定義參數G、F1、F2、L、L0、G′、N的數值，按照式（4）和式（5）建立F2′和F1′的公式[3]。

2.2 板簧載荷

板簧負載狀態下的弧高與板簧所承受的載荷密切相關，因此首先需確定板簧的簧載質量。

前橋（包含制動器、轉向臂、輪轂罩等裝配在前橋上的部件）、后橋（包含制動器、轉向臂、輪轂罩等裝配在后橋上的部件）及輪胎是裝配在懸架下方，因此這些部件的質量不會加載在懸架板簧上，傳動軸一端是裝配在后橋上，另外一端裝配在變速器上，中間部分還與車架相連，因此可認為傳動軸質量的1/2加載在后懸架上，前后懸架自重的1/4也分別由前后懸架承載，另外的3/4為非簧載質量，前后板簧的非簧載的部件如表1所示[4]。

表1 前后板簧非簧載部件

前后懸架的簧載質量即為前后輪的負荷減去非簧載總質量，單邊簧載質量分別為前后懸架簧載質量的一半，設前后板簧在空載狀態下的單邊簧載質量分別為G1和G2，在滿載狀態下的單邊簧載質量分別為G1′和G2′。

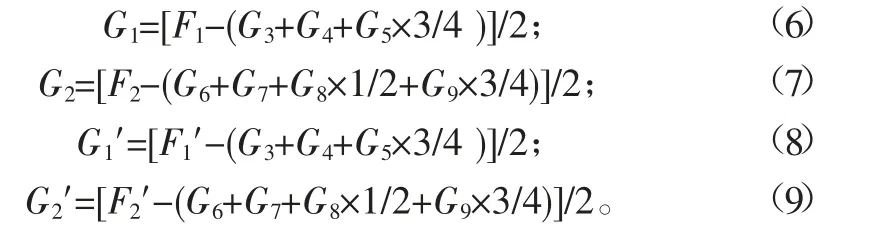
在CATIA中輸入設計已定義參數G3、G4、G5、G6、G7、G8、G9，按照式（6）～式（9）建立G1、G2、G1′和G2′的公式。

2.3 板簧弧高

板簧在負載狀態下的弧高為其在夾緊狀態下無負荷弧高減去負載質量對其的壓縮量即撓度[5]：

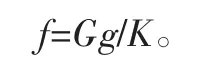
式中：f為撓度；G為簧載質量；g為重力比例系數；K為懸架剛度。

設前板簧在夾緊狀態下的無負荷弧高為H1，前板簧的剛度為K1；前板簧在空載和滿載狀態下的弧高H3和H3′，得到如下公式：

懸架一般會設計有主簧和副簧疊加的狀態，在空載狀態下副簧一般不會啟動工作，滿載狀態下，如果后懸單邊簧載質量超過了副簧開始工作時的臨界載荷，則副簧也開始工作，設以上臨界載荷為Gc。設后板簧在夾緊狀態下的無負荷弧高為H2，后主簧的剛度為K2，主副簧的總剛度為K3；后板簧在空載和滿載狀態下的弧高為H4和H4′，得到如下公式：

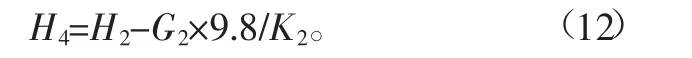
當G2′≤Gc時，

當G2′＞Gc時，

在CATIA中輸入設計已定義參數H1、H2、K1、K2、K3、Gc、g，按照式（10）～式（14）建立H3、H3′、H4和H4′的公式。

2.4 板簧弦的長度確定

隨著載荷的變化，板簧弧高h會發生變化，進而也會引起弦長l發生變化，而板簧本身的長度s、板簧包耳的半徑r、板簧中間騎馬螺栓距u均為設計固定值。

弦長的計算公式如下[6]：

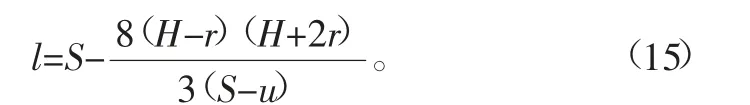
在滿載狀態下，板簧弧高會進一步變小，若h＜r，則上式中的弧高需換成(2r-h)，此時l計算公式如下：

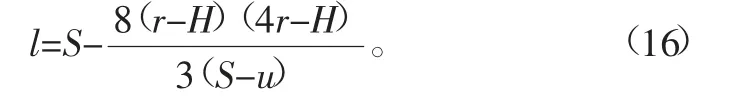
設前后板簧在空載狀態下弦長分別為l1和l2，在滿載狀態下弦長分別為l1′和l2′，前后板簧本身的長度分別為s1和s2、前后板簧包耳半徑分別為r1和r2、前后板簧騎馬螺栓距分別為u1和u2。在CATIA中輸入設計已定義參數s1、s2、r1、r2、u1、u2，根據h與r的關系，按照式（15）和式（16）建立l1、l2、l1′和l2′的公式。

2.5 確定輪胎中心

輪轂中心線可近似認為與輪胎中心線重合，圖1為前橋和前懸裝配在一起的狀態，圖3為后橋和后懸裝配在一起的狀態，弦中線點位置和弧高是變量，懸架中間處板簧及其墊片的厚度d2和輪轂中心線到懸架和橋接觸點的垂直距離h2均為設計常量。

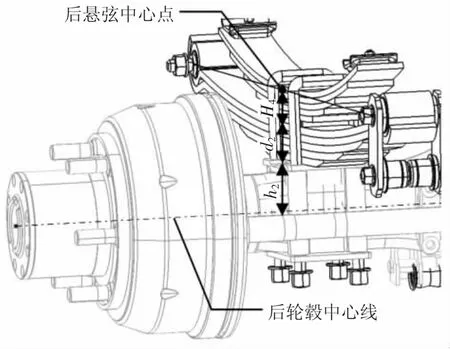
圖3 后懸和后橋裝配示意圖

設前懸中間處板簧及其墊片的厚度為d1，前輪轂中心線到前懸架和前橋接觸點的垂直距離為h1，在CATIA中輸入設計常量d1和d2、h1和h2的值。在CATIA中建立幾何圖形集，確定輪胎中心點，以空載狀態下前輪為例，制作程序如下：1）輸入前懸前卷包耳襯套中心點和前懸吊耳襯套中心點坐標，其中Y坐標可不輸入實際值，直接輸入0即可（下文中各點的Y值均為0），X和Z坐標必須是實際值。2）以前懸吊耳襯套中心點為中心、以吊耳半徑為半徑在Y0平面上作一個圓弧，那么前懸后卷包耳襯套中心點就在這個圓弧上運動；前懸的弦即為前懸前卷包耳襯套中心點與前懸后卷包耳襯套中心點的連線；弦的長度設置成公式，等于2.4節中輸出的參數l1；由以上3個約束條件便可確定弦的位置。3）在弦上取中心點，該中心點沿弦的法線方向移動，移動的距離設置成公式，等于2.3節中輸出的參數H3，移動后的點即為空載前板簧上表面中心點；將空載前板簧上表面中心點沿弦的法線方向移動，移動的距離設置成公式，等于輸入的參數d1，移動后的點即為空載前板簧與前橋接觸面的中心點；再將空載前板簧與前橋接觸面的中心點沿弦的法線方向移動，移動的距離設置成公式，等于輸入的參數h1，移動后的點即為空載狀態下前輪轂中心點，也就是空載狀態下的前輪中心點。

后輪中心點及滿載狀態下的前后輪中心點在CATIA中的確定方法與空載狀態下前輪中心點的確定方法相同，可直接將上述幾何圖形集“空載前輪心確定”進行復制，對名稱和相關參數進行更改即可。

2.6 制作地面

輪胎中心線的位置確定后，只需要確定輪胎在一定載荷狀態下的半徑，即可確定地面位置。根據輪胎的型號可在國標中查到新胎的設計外直徑、負荷能力及靜負荷半徑等參數[7]。設所設計車型的輪胎新胎半徑為R1，單胎負荷能力為G10，在額定負荷下的靜負荷半徑為R2，以上參數均可在標準中查到，由此可粗略計算出輪胎的變形系數為

設在空載和滿載狀態下，前輪胎的靜負荷半徑分為R3和R3′；在空載和滿載狀態下，后輪胎的靜負荷半徑分為為R4和R4′，那么R3、R3′、R4和R4′可以分別通過以下公式計算出來：

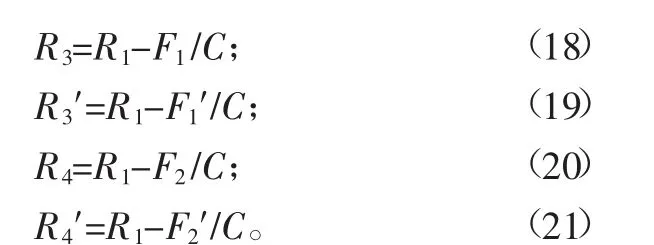
在CATIA中輸入設計參數G0、R1和R2，并按照式（17）～式（21）在CATIA中建立公式參數。

在CATIA中再建立幾何圖形集，以2.5節中確定的空載和滿載狀態下前輪和后輪的輪心為中心、在Y0平面上作一個圓，圓的半徑設置成公式，分別作出空載狀態下前輪圓和后輪圓的外公切線、滿載狀態下前輪圓和后輪圓的外公切線，即得到空載和滿載狀態下的地面線。

3 結論

用以上方法在CATIA中建立地面線的制作模型，對于不同的車型，只需要更改表1中輸入的參數數值，便可直接生成目標車型在不同狀態下的地面線，方便快捷。

通過對一輛輕型載貨汽車的地面線進行理論設計和實物測量的對比，實際稱重得到該車在空載狀態下前軸軸荷為1534.5 kg，后軸軸荷為1051.5 kg，獲取該車型在表1中列出的相關部件的數值，輸入到CATIA中建立的地面線模型中，得到理論地面線。測量該車車架特定位置2處車架上平面到地面的垂直距離，以上2處實際測量值比理論測量值分別小4.3 mm和4.1 mm，該誤差不應影響設計理論校核。