基于2021年江蘇省高考物理卷第14題的變式類型分析及解題策略

江蘇 呂朝陽 王 虹

2021年江蘇省高考物理卷第14題是一道模型新穎、設計精巧的學習探索類情境綜合試題，其顯著特征是在系統中有一個或多個物體做勻速圓周或非勻速圓周運動，考查的知識點有力的平衡、圓周運動(向心力與向心加速度)、彈性勢能和功能關系等，對學生的思維品質和關鍵能力有很好的檢測作用。受此影響，在此后的各地高三模擬考試卷中出現了大量的變式題。現將此類變式題型歸類分析，并研究和總結解題策略。

【高考原題】如圖1所示的離心裝置中，光滑水平輕桿固定在豎直轉軸的O點，小圓環A和輕質彈簧套在輕桿上，長為2L的細線和彈簧兩端分別固定于O和A，質量為m的小球B固定在細線的中點，裝置靜止時，細線與豎直方向的夾角為37°，現將裝置由靜止緩慢加速轉動，當細線與豎直方向的夾角增大到53°時，A、B間細線的拉力恰好減小到零，彈簧彈力與靜止時大小相等、方向相反，重力加速度為g，取sin37°=0.6，cos37°=0.8，求：

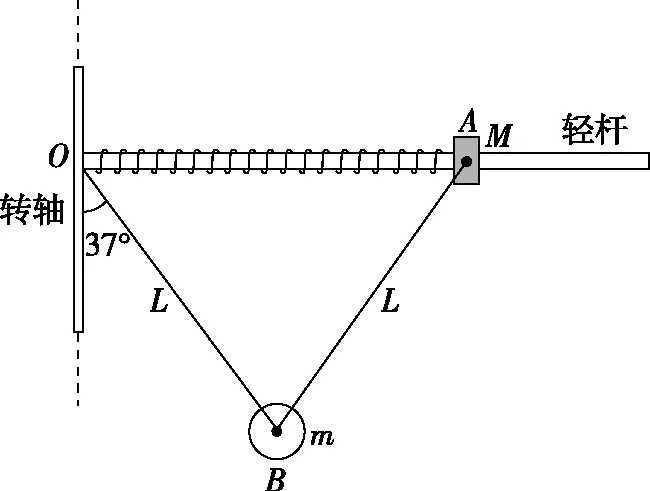
圖1

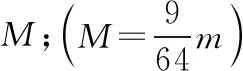
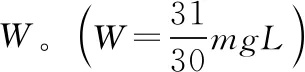
變式類型一、含彈簧的多物體系統

在處理含彈簧且系統內有一個或多個物體做圓周運動的綜合題時，要從以下4個方面進行突破。

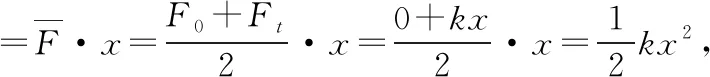
②找準系統中各物體之間力的聯系。多物體系統中，物體之間一般是通過輕繩、輕桿或輕彈簧連接，需要通過分析輕繩、桿和彈簧中力的大小和方向來尋找物體間力的聯系，這也是解決多物體系統問題常見的思路之一。

③分析系統中做圓周運動物體的向心力的來源。在這類題型中，做圓周運動物體的受力一般相對較復雜，對應的解題思路是將物體所受的力均沿半徑方向和垂直半徑的方向進行正交分解，沿著半徑方向的合力就是向心力。

④透析功和能的一一對應關系以及能量的轉化情況。當研究對象為系統時，如果只發生動能和重力勢能、彈性勢能之間的相互轉化，則利用機械能守恒定律解題；若有外力對系統做功或外界有能量注入系統，則一般利用能量的轉化和守恒定律或功能關系(外界對系統所做的功等于系統各種能量的增量的和)列方程求解。若研究對象為單個物體，則一般利用動能定理列方程求解。

該變式類型又可細分為以下2類題型。

1.初、末狀態彈簧的彈性勢能相同

【變式1】(2022·江蘇高三聯考·14)如圖2所示，小球A、B、C分別套在光滑“T”型桿的水平桿MN和豎直桿OP上，小球A、B由輕彈簧相連，小球C由兩根不可伸長的等長細線分別與小球A、B相連，水平桿MN可以繞豎直桿OP在水平面內轉動。靜止時，細線AC、BC與桿OP的夾角均為θ=37°，小球A、B間的距離x1=0.6 m。已知細線的長度l=0.5 m，彈簧原長x0=0.7 m，球A、B的質量mA=mB=0.5 kg，小球C的質量mC=0.48 kg，三個小球均可視為質點，取重力加速度g=10 m/s2，sin37°=0.6，cos37°=0.8。

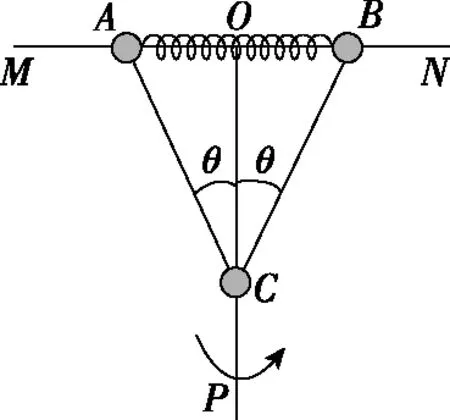
圖2

(1)系統靜止時，求彈簧對A的彈力大小F；

(2)使水平桿MN勻速轉動，穩定時細線AC與MN桿的夾角α=37°(圖中未標出)，求MN桿轉動的角速度ω；

(3)求系統從靜止到以(2)中的角速度勻速轉動過程中，外力所做的功W。

【解析】(1)對小球C受力分析，有2Tcos37°=mCg

對小球A受力分析，有F=Tsin37°

代入數據得F=1.8 N

(2)系統靜止時，彈簧的壓縮量Δx1=x0-x1=0.1 m，當細線AC與MN桿的夾角α=37°時，彈簧的伸長量Δx2=x2-x0=2lcos37°-x0=(0.8-0.7) m=0.1 m，故此時彈簧的彈力大小F1=F=1.8 N

對小球C受力分析，有2T1sin37°=mCg

對小球A受力分析，有T1cos37°+F1=mAω2lcos37°

聯立解得ω=5 rad/s

(3)由于彈簧在初末狀態的形變量相同，故彈簧的彈性勢能也相同。根據功能關系，外力做功等于系統機械能的增加，有W=ΔEpC+2ΔEkA

而ΔEpC=mCgl(cos37°-sin37°)

代入數據解得W=2.48 J

【點評】該題主要考查了力的平衡、勻速圓周運動以及功能關系等重要知識點，其主要特點是，在初、末狀態彈簧分別是壓縮或伸長的，但形變量恰好相同，即彈簧在初、末狀態的彈性勢能相同，故在利用功能關系列方程時，就不需要考慮彈簧彈性勢能的變化。同時，該題型又是一個軸對稱的結構，小球A和B的角速度和動能相同，線速度、向心力、向心加速度的大小相同。根據對稱性還可以分析出，兩根繩子對小球C拉力的大小也相同。這些都是在解題時需要注意的。

2.初、末狀態彈簧的彈性勢能不同

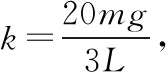
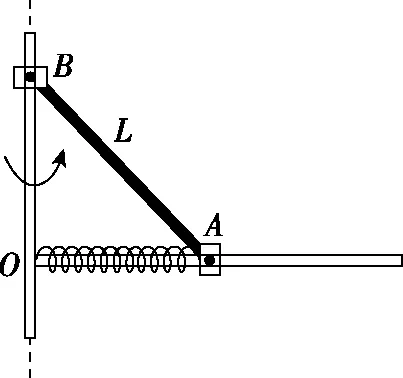
圖3

(1)裝置靜止時，小環A受桿的摩擦力大小f；

(2)輕桿與豎直方向夾角為53°時的角速度ω；

(3)輕桿與豎直方向夾角從37°變化到53°的過程中，豎直轉軸對裝置所做的功W。

【解析】(1)裝置靜止時，設桿對B的作用力為F，則

A受力平衡f=Fsin37°

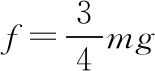
(2)輕桿與豎直方向的最終夾角為53°時，彈簧彈力

以A、B為整體，分析豎直方向的受力，可知A與水平桿之間的正壓力FN=2mg

A受摩擦力fm=μ·FN=μ·2mg=mg

對B，設桿對B的作用力為F1，則F1cos53°=mg

對A分析fm+Fk-F1sin53°=mω2Lsin53°

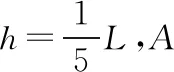
摩擦力所做的功Wf=fm·Δx=0.2mgL

對系統，根據功能關系W+mgh-Wf=EkA+Ep

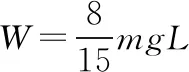
【點撥】該題主要考查了力的平衡、勻速圓周運動以及功能關系等重要知識點，其主要特點是彈簧在初、末狀態的形變量不同，但題干中給出了彈簧彈性勢能的表達式，故在利用功能關系列方程時，將表達式直接代入即可。若題干中沒有給出彈性勢能的表達式，則需根據彈簧彈力做功跟彈簧端點的位移大小(即彈簧形變量的大小)成正比的關系，推導出彈性勢能的表達式。另，本題中連接A、B兩圓環的是輕質剛性桿，是通過可以自由轉動的鉸鏈進行鏈接的，故輕質桿對兩圓環的彈力均沿著桿的方向。

變式類型二、不含彈簧的多物體系統

在處理不含彈簧且系統內有一個或多個物體做圓周運動的綜合題時，一般的解題思路如下。

①力的觀點。該類題型中，做圓周運動的物體的受力一般較為復雜，將力沿半徑方向和垂直半徑的方向進行正交分解，則沿半徑方向的合力即為向心力。若物體做勻速圓周運動，其合外力提供向心力，則沿垂直半徑方向(即切線方向)分力的合力為零。

②能的觀點。研究對象為系統時，若只發生動能與勢能之間的相互轉化，則利用機械能守恒定律列方程解題；若有外力對系統做功或有其他形式的能參與轉化，則需利用功能關系或能量的轉化和守恒定律列方程解題。研究對象為單個物體時，由于往往涉及變力做功，則一般列出動能定理的方程解題。

③牽連速度觀點。將桿連或繩連物體的速度，沿著繩或桿的方向及垂直于繩或桿的方向進行正交分解，則物體在沿桿或繩方向的分速度相同。但一定要注意的是，對繩連或桿連的物體來說，雖然它們沿著繩或桿的分速度是相同的，但它們的加速度在沿著繩或桿方向的分量，在一般情況下都是不同的。

④動量的觀點。該類題型若涉及沖量，則需要列出動量定理的方程求解；若系統合外力為零，則需列出動量守恒定律的方程求解。

該變式類型又可細分為以下3類題型。

1.考查水平面內的勻速圓周運動

【變式3】(2022·揚州一模·14)(改編)如圖4所示，輕桿的上端可繞O處的光滑鉸鏈在豎直平面內自由轉動，小球固定在輕桿上Q點，用細繩連接小物塊與小球，繩子穿過鉸鏈正下方P處的小孔。現用手沿繩方向拉住小球，使小球和物塊保持靜止，此時∠OQP=90°，∠POQ=37°。已知小球和小物塊的質量m均為1 kg，輕桿長度L=1 m，重力加速度g取10 m/s2，忽略一切摩擦，sin37°=0.6，sin53°=0.8，則：

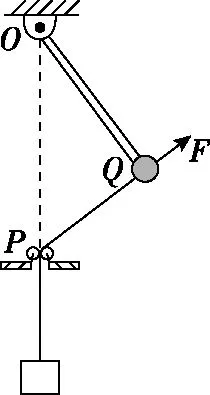
圖4

(1)求松手后，小球運動到最低點時的速度大小v；

(2)求松手后，小球在左側最高點時繩對小球的拉力大小T；

(3)若在松手的瞬間給小球一個垂直紙面向里的瞬時沖量I，小球恰能在水平面內做勻速圓周運動，求I的大小。

【解析】(1)撤去F后，小球、物塊組成的系統機械能守恒，小球運動到最低點時，物塊的速度為零

小球下降的高度h1=L(1-cos37°)

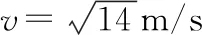
(2)如圖5所示，小球在左側最高點時，小球和物塊的速度均為零，物塊與小球沿繩方向加速度大小相等。

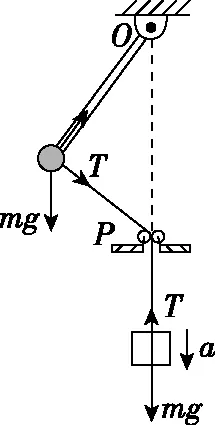
圖5

小球：T+mgsin37°=ma

物塊：mg-T=ma

解得T=2 N

(3)設桿對小球的力為FN，繩對小球的力FT=mg，設小球運動的速度大小為v1，則

FNcos37°=mg+mgsin37°

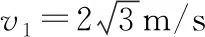
【點撥】該題主要考查了機械能守恒定律、瞬時加速度、牽連速度、勻速圓周運動以及動量定理等重要知識點，其主要特點是題干字數雖不多，但信息量大，考查知識點多，綜合性強。在本題(1)中，要能根據牽連速度的相關知識判斷出，當小球運動到最低點時小物塊的速度為零；本題的(2)中，由于小球和物塊的速度在此刻為零，不存在相對向心加速度，故而它們沿著繩的加速度相同。但如果存在相對向心加速度，則輕繩相連的兩物體沿繩方向的分加速度可能不同。

2.考查水平面內的非勻速圓周運動

【變式4】(2022·南通七市聯考·14)(改編)如圖6甲所示，在光滑水平面上有A、B、C三個小球，A、B兩球分別用水平輕桿通過光滑鉸鏈與C球連接，兩球間夾有勁度系數足夠大、長度可忽略的壓縮輕彈簧，彈簧與球不相連。固定住C球，釋放彈簧，球與彈簧分離瞬間桿中彈力大小F=10 N。已知A、B兩球的質量均為m1=0.2 kg，C球的質量m2=0.4 kg，桿長L=1.0 m，彈簧在彈性限度內。

(1)求彈簧釋放的彈性勢能Ep；

(2)若C球不固定，求釋放彈簧后C球的最大速度v；

(3)若C球不固定，求球與彈簧分離后到兩桿間夾角第一次為θ=120°的過程中(圖6乙)，桿對B球所做的功W。

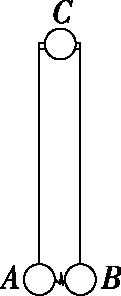
甲

【解析】(1)由對稱性可知球，與彈簧分離時兩球的速度大小相等，設為v0

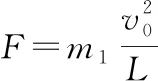
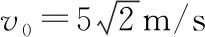
(2)如圖7所示，設兩桿夾角為θ時，C球的速度為vC，將B球的速度正交分解為vx和vy，根據對稱性可知，vAy=vBy=vy，vAx=vBx=vx

圖7

y軸方向動量守恒，則0=m2vC-2m1vy

①

系統機械能守恒，則

②

B、C兩球沿桿方向的分速度相同，則

③

故當θ=180°時，C球的速度最大，且最大值

v=vC=5 m/s

(3)在(2)的①②③三式中，將θ=120°代入，可得

以B球為研究對象，利用動能定理

【點撥】該題主要考查了動量守恒定律、機械能守恒定律、牽連速度和動能定理等重要知識點，其最大的特點是A、B兩球雖相對C球做圓周運動，但由于C球不固定，使得A、B兩球的運動形式比較復雜，因此該題對思維能力的要求很高，需要具有較強的空間想象能力、邏輯推理能力以及利用數學工具處理物理問題的能力。在解答本題時，一是需要利用對稱的觀點解題，要能根據本題中三個小球受力及運動的特點，判斷出C球的速度是沿著兩桿夾角的角平分線方向，A球和B球沿x軸方向的分速度大小相等、方向相反以及沿y方向的分速度相同；二是在利用動量守恒定律解題時，要能利用運動的合成和分解知識將復雜的運動簡單化，把A球和B球的速度在x軸和y軸兩個方向進行正交分解，再在這兩個方向上利用動量守恒定律分別列方程求解。

3.考查豎直平面內的非勻速圓周運動

【變式5】(2022·如皋市三模·15)如圖8所示，圓心為O、半徑為R的圓環固定在豎直平面內，O1、O2為兩個輕質定滑輪頂點，O1在O點正上方2R處，跨過定滑輪的輕繩一端連接著套在圓環上的小球A，另一端連接著小球B。用一豎直向下的外力作用于B，A、B靜止于圖示位置，OP與豎直方向的夾角為60°，撤去外力后，A、B開始運動，B始終不與滑輪碰撞。已知A、B的質量分別為4m、m，重力加速度為g，圓環與繩不接觸，不計一切摩擦。

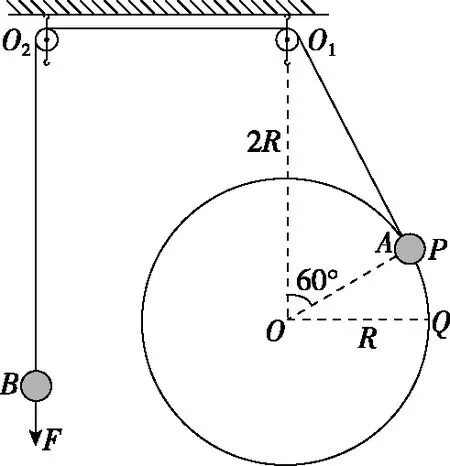
圖8

(1)求外力的大小F；

(2)當A運動到圓心等高處的Q點時，求A的向心力大小Fn；

(3)若撤去外力的同時給A施加沿輕繩斜向右下的瞬時沖量I，A恰能運動到圓環的最高點，求：

①I的大小；

②A從圓環最低點運動到最高點過程中輕繩對A做的功W。

【解析】(1)對A：4mgsin60°=T

對B：T=mg+F

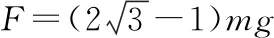
(2)A、B系統機械能守恒

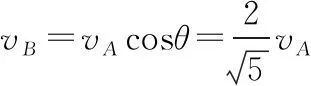
(3)①對A、B：I=5mv0

當小球A恰好運動到圓環最高點時，A、B球的速度均為零，系統機械能守恒

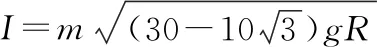
②在小球A從圓環最低點運動到最高點，初、末狀態小球B的速度均為零，對B利用動能定理

WTB=-mg(3R-R)=-2mgR

而W=-WTB

解得W=2mgR

【點撥】該題主要考查了力的平衡、圓周運動、機械能守恒定律、牽連速度和動能定理等重要知識點，該題與此前例題的最大區別是，物體在豎直平面內做非勻速圓周運動。在處理此類綜合問題時，還需注意三點。一是要分清物體在豎直平面內的運動是屬于“繩模型”還是“桿模型”。本題屬于“桿模型”，故小球A恰能運動到圓環的最高點時速度為零。二是在本題(3)①中，雖題干中指出，在撤去外力的同時，給小球A施加沿輕繩斜向右下的瞬時沖量I，但I≠mAvA。因為兩小球是用輕繩連接在一起的，理想輕繩不能被拉長，繩中的拉力可以突變，故I=(mA+mB)v。三是在本題(3)②的解答中，在求輕繩對小球A所做的功時，并沒有直接以小球A為研究對象，而是選取小球B為研究對象，利用動能定理先求出繩子對小球B所做的功，再根據繩對A、B做功的大小相等、一正一負的結論來巧妙解題。如果兩個小球是用輕桿相連，那么這個結論依然成立。但當連接兩個小球的不是輕繩或輕桿，而是彈性繩或彈簧時，由于兩個小球沿彈性繩或彈簧方向的位移一般不同，此結論將不再成立。

結語

高考是指揮棒，所以研究高考真題以及相應的變式習題就非常重要。在處理含彈簧或不含彈簧、有一個或多個物體做圓周運動的綜合題時，一般的解題思路如下。

1.在對做圓周運動的物體正確受力分析后，一般將物體受力沿半徑方向和垂直半徑方向進行正交分解，再列兩個方向上對應方程的解題思路。這樣做的好處是，既可以列出向心力公式，也可以求出或表示出繩或桿中的張力大小，而此張力往往是聯系物體間關系的橋梁之一。

2.對含彈簧的多物體系統來說，要通過分析和計算，判斷在初、末狀態彈簧形變量的大小關系，進而判斷出彈簧彈性勢能的變化情況。一般來說，出現彈簧在初、末狀態的形變量恰好相等的這種情況相對較多。如果彈簧在初、末狀態的形變量不相等，一般不會考查彈性勢能大小的表達式。

3.當只發生動能與勢能間的相互轉化時，系統的機械能是守恒的，需要列出系統機械能守恒定律的方程進行求解；當外界對系統做功或外界有其他能量注入系統時，一般要列出功能關系或能量轉化和守恒定律的方程進行求解；當題目要求的是內力對單個物體所做的功時，一般采用動能定理進行求解。

4.當系統中的物體是通過輕繩或輕桿相連接時，一般都需要將物體的速度沿著繩或桿，以及垂直于繩或桿這兩個方向進行分解，在輕繩沒有松弛的前提下，物體沿繩或桿的分速度是一定相同的。但物體沿繩或桿的分加速度不一定相同，具體情況還應再具體分析。