基于圖像復原處理的近場MVDR聲圖測量方法

賀 歡，王逸飛

(1.黃河科技學院信息工程學院，河南 鄭州 450000;2.東南大學信息工程學院，江蘇 南京 210000)

0 引言

聲圖測量是一種通過聚焦波束形成方法實現近場精確定位的技術，被廣泛應用于空氣聲學、水聲學和醫學超聲領域的聲學成像技術[1-3]。由于自適應聚焦波束形成方法可根據噪聲自適應調整陣列各通道加權值，實現信噪比最大輸出，其所得聲圖峰值較為尖銳，空間分辨率較好，被廣泛應用于聲圖測量中[4-7]。但該類方法需要在一定輸入信噪比下才能發揮其性能優勢，當信噪比較低時，性能變差，甚至使目標空間位置分布估計結果出錯[8]。為了降低近場MVDR聲圖測量中背景級，研究學者提出采用二階錐凸優化、分子陣處理等方法降低其背景級，但存在如下問題：二階錐凸優化方法針對切比雪夫濾波方法存在的問題做了進一步改善，可以同步設置波束形成旁瓣級、主瓣寬度等多個指標，實現了波束形成優化，但設置這些參數需要將陣列模型結構一起納入考慮范圍，如果模型結構設置存在問題，將得不到最優結果；分子陣預處理方法在陣列孔徑有限情況下，對降低波束形成背景級有限[9-11]。

針對基于最小方差無畸變響應(MVDR)近場聲圖測量中聲圖背景級較高問題，本文借鑒圖像復原理論中的解卷積技術在陣列信號處理中的應用實例[12-16]，提出一種基于圖像復原處理的近場MVDR聲圖測量方法(本文稱之為DMVDR方法)。該方法首先根據近場MVDR聲圖測量方法(本文稱之為MVDR方法)輸出聲圖特性，采用類狄利克函數作為聲圖點擴展函數(point scattering function，PSF)；然后利用PSF和R-L方法對MVDR方法輸出模糊聲圖進行解卷積，得到清晰聲圖估計結果，降低模糊聲圖背景級及其影響。

1 MVDR方法

1.1 信號模型

如圖1所示，在線列陣近場區域，存在K個獨立目標，其位置分別為(RK,ΘK)=[(R1,θ1),(R2,θ2),…,(RK,θK)]，則線列陣各傳感器接收數據可表示為：

X(f)=A(RK,ΘK)S(f)+V(f)，

(1)

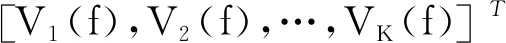
圖1 近場聲圖測量示意圖Fig.1 Schematic diagram of near-field source measurement

在近場聲傳播中，目標聲源輻射信號按球面波傳播到各傳感器位置處，則陣列流形矩陣A(RK,ΘK)具體形式為：

(2)

1.2 MVDR聲圖測量

針對式(1)所示數據，其協方差矩陣RX(f)可表示為：

RX(f)=X(f)HX(f)=
A(RK,ΘK)HRS(f)A(RK,ΘK)+RV(f)，

(3)

式(3)中，RS(f)為目標信號分量協方差矩陣，RV(f)為背景噪聲分量協方差矩陣，(·)H為共軛轉置。

此時，近場MVDR聲圖測量最優權向量可表示為：

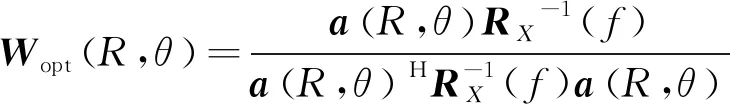
(4)

式(4)中，

為當前掃描點(R,θ)到第n∈[1,N]傳感器水平距離，θ為當前掃描點對線列陣法線方向角度，R為當前掃描點相對線列陣中心位置(參考點)距離。

根據獲得的權向量最優解，可得到當前掃描點(R,θ)對應的聲圖測量值。

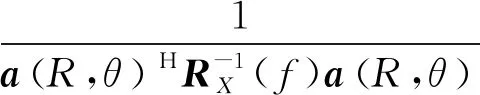
(5)

對協方差矩陣RX(f)進行特征分解，可得：

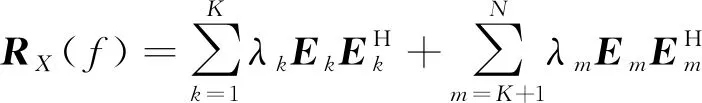
(6)

式(6)中，λk和Ek分別為目標信號分量對應特征值和特征向量，λm和Em分別為背景噪聲分量對應特征值和特征向量。

此時，式(5)可分解為：

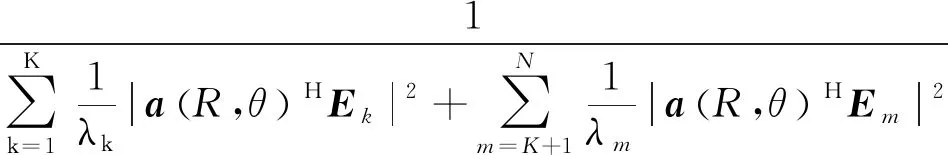
(7)

當掃描點(R,θ)屬于空間位置(RK,ΘK)，由于Em與a(Rk,θk)正交性，式(7)可簡化為：

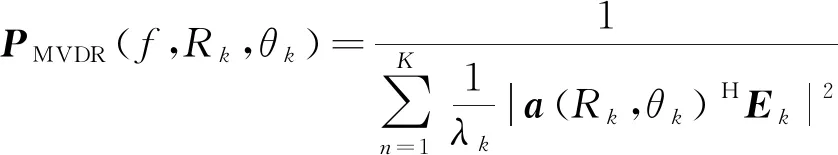
(8)

由式(8)可知，當掃描點(R,θ)屬于空間位置(RK,ΘK)，MVDR方法具有自動消除噪聲分量和保留目標信號分量能力，使信號子空間更好地作用于目標參數估計，理想情況下，MVDR方法聲圖測量結果具有最優估計效果。

所以，當掃描點到目標聲源空間位置時，有R=Rk、θ=θk，此時PMVDR(f,Rk,θk)幅度最大，所以通過搜索最大峰值位置即可實現對目標聲源空間位置分布值估計。

2 DMVDR方法

2.1 原理分析

對于空間位置(Rk,θk)處的目標聲源，為了后續分析方便，在設定最大掃描距離Rmax上，MVDR方法處理過程可表示為對空間位置(ΔRsinθ,ΔRcosθ)分布值的估計，ΔR=R/Rmax。此時，式(7)可進一步表示為：

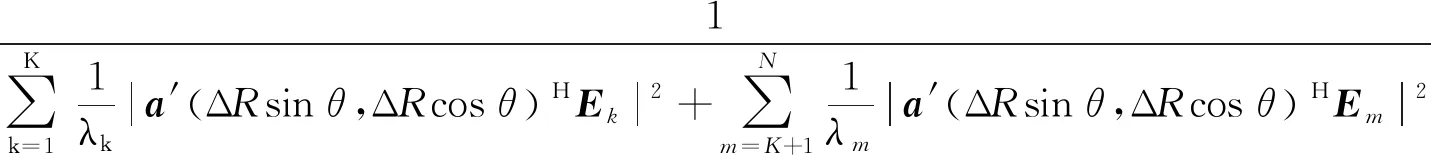
(9)

式(9)中，a′(ΔRsinθ,ΔRcosθ)=[ej2πfτ1′,ej2πfτ2′,…,ej2πfτN′]T，τn′=(Rn-RmaxΔR)/c=τn。

如圖1所示，令目標聲源在(ΔRsinθ,ΔRcosθ)空間位置分布為Ω，則Ω中的一個元素Ω(ΔRsinθ,ΔRcosθ)可表示為：

Ω(ΔRsinθ,ΔRcosθ)=
Aδ(ΔRsinθ-ΔRksinθk,ΔRcosθ-ΔRkcosθk)，

(10)

式(10)中，A為目標聲源幅度，δ為二維狄利克函數。

由此可得，MVDR方法所得聲圖PMVDR(f,ΔRsinθ,ΔRcosθ)可比作是對Ω的估計，即PMVDR(f,ΔRsinθ,ΔRcosθ)可表示為h(ΔRsinθ,ΔRcosθ)與Ω的二維卷積。

PMVDR(f,ΔRsinθ,ΔRcosθ)=
Ω(ΔRsinθ,ΔRcosθ)**h(ΔRsinθ,ΔRcosθ)+V，

(11)

式(11)中，**為二維卷積運算。

由式(11)可知，在已知h(ΔRsinθ,ΔRcosθ)時，可通過解卷積處理，實現對Ω估計，進而獲得目標聲源空間位置(ΔRsinθ,ΔRcosθ)的估計值[16]。

在目標聲源為點源情況時，聲圖測量方法對目標聲源的輸出響應可比作為聲圖探針，即為目標聲源在聲圖上的像，在線列陣有效孔徑無限大時，探針在目標聲源位置處的理想響應為一個二維狄利克函數[16]。因此，可利用一個“類狄利克函數”構造聲圖PMVDR(f,ΔRsinθ,ΔRcosθ)的點擴展函數，即

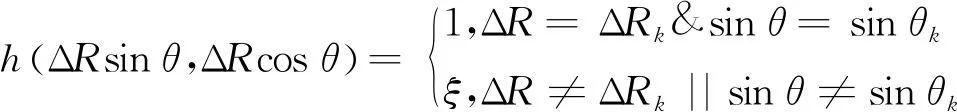
(12)

式(12)中，ξ∈(0,1)的常數。

將式(9)中，聲圖PMVDR(f,ΔRsinθ,ΔRcosθ)表示成二維卷積形式為：

PMVDR(f,ΔRsinθ,ΔRcosθ)=
Π(ΔRsinθ,ΔRcosθ)**h(ΔRsinθ,ΔRcosθ)+V,

(13)

式(13)中，Π(ΔRsinθ,ΔRcosθ)表達式為：

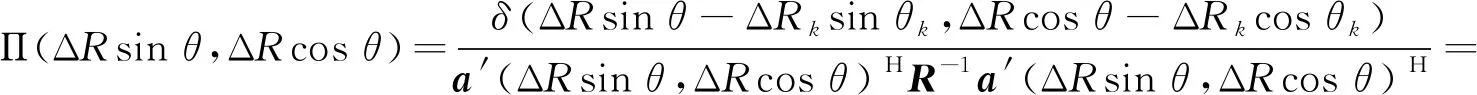
(14)

2.2 聲圖復原

針對MVDR方法輸出聲圖PMVDR(f,ΔRsinθ,ΔRcosθ)中背景級較高的問題，本文利用Richardson-Lucy方法[15-16]對式(13)進行二維解卷積，估計Π(ΔRsinθ,ΔRcosθ)。

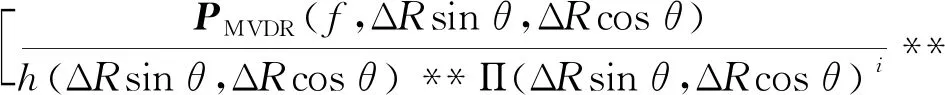
(15)

采用式(15)進行迭代時，ξ取為歸一化聲圖平均值，即為：

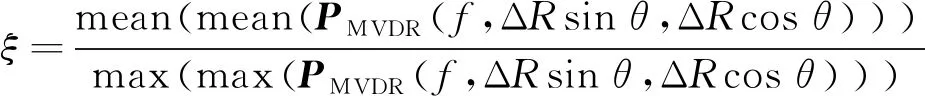
(16)

式(16)中，mean(·)為均值運算符， max(·)為最大值運算符，在均值求取時將最大值周圍值置零。

式(15)處理后的聲圖可表示為：

PDMVDR(f,ΔRsinθ,ΔRcosθ)=Π(ΔRsinθ,ΔRcosθ)I。

(17)

3 數值仿真分析

為了驗證本文方法的可行性和有效性，仿真中線列陣由32個傳感器組成，相鄰傳感器間距為4 m，采樣率為5 kHz，一次處理數據總量為5 kB。接下來采用常規聚焦波束形成方法(CBF方法)、MVDR方法、文獻[11]方法和DMVDR方法進行對比分析。

3.1 單目標聲源情況

仿真中，假定目標聲源相對線列陣為點源，目標聲源位于相對線列陣陣中心(80 m,0°)位置處，目標聲源輻射頻率為[160 Hz,200 Hz]寬帶信號，背景噪聲為高斯白噪聲，各傳感器拾取數據所含信噪比為SNR。仿真掃描平面為水平距離[20 m,200 m]、方位角度[-90°,90°]，將該區域按掃描網格劃分，網格間距為2 m，角度1°。

圖2—圖4分別給出了4種方法在SNR=-5,-10,-15 dB情況下所得距離R=80 m處不同角度下聲圖測量值。

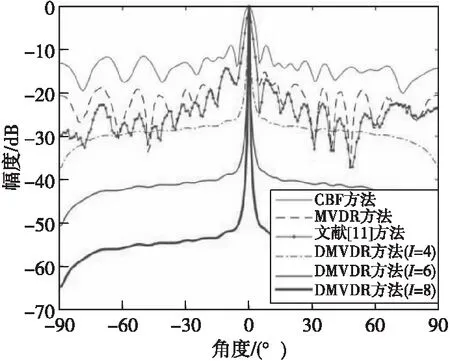
圖2 4種方法所得聲圖測量值(SNR=-5 dB)Fig.2 One-dimensional source distribution map of four methods(SNR=-5 dB)

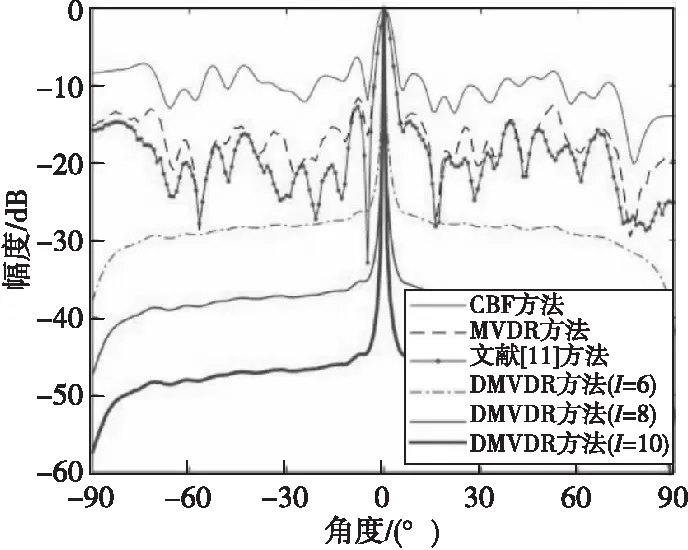
圖3 4種方法所得聲圖測量值(SNR=-10 dB)Fig.3 One-dimensional source distribution map of four methods(SNR=-10 dB)

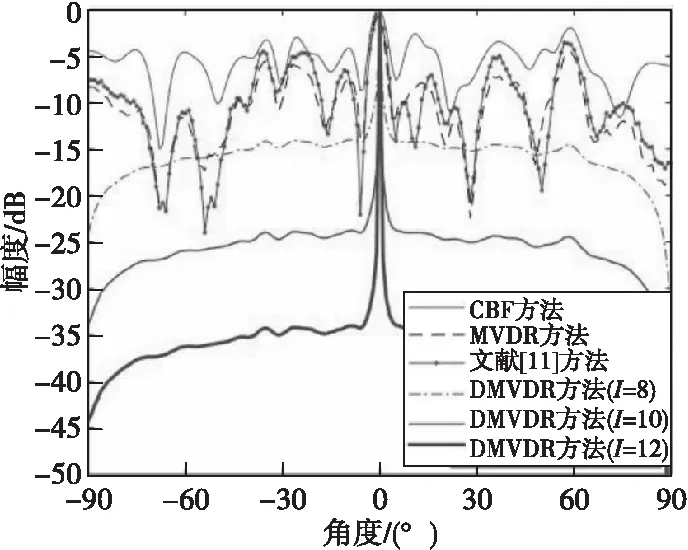
圖4 4種方法所得聲圖測量值(SNR=-15 dB)Fig.4 One-dimensional source distribution map of four methods(SNR=-15 dB)

由圖2—圖4結果可得：當SNR=-5、SNR=-10、-15 dB時，不同方法輸出背景級如表1所示。

由表1可知：MVDR方法通過約束目標位置處信號功率不變，噪聲和非目標位置處功率最小，相比CBF方法，降低了聲圖背景噪聲級；文獻[11]方法通過分子陣處理，在高信噪比下降低了聲圖背景級，但在低信噪比下相比MVDR方法改善效果有限；而DMVDR方法通過4次迭代解卷積即可實現優于MVDR方法的效果，且隨著I變大，其輸出背景級降低越大，背景更平滑，遠低于CBF方法、MVDR方法和文獻[11]方法，具有更優的目標位置估計能力。

另外，DMVDR方法相比MVDR方法，在仿真中進行解卷積運算，該方法增加了I×R×(2Θ2+Θ)乘法和I×R×Θ2加法運算，R為聲圖掃描距離個數算法復雜度增加了，Θ聲圖掃描角度個數，算法復雜度增加。采用 Inter Corei7 2核處理器，在Matlab2019a編程環境下，進行1次處理DMVDR方法所需運算時間為0.312 2 s(I=12)，由此可見，DMVDR方法可滿足實際應用中的實時性要求。

表1 不同方法輸出背景級Tab.1 The output ground level of different methods

3.2 雙目標聲源情況

采用兩個目標聲源對DMVDR方法有效性進行分析論證。仿真中，假定目標聲源相對線列陣為點源，兩目標聲源位于相對線列陣陣中心(80 m,-2°)和(80 m,2°)位置處，目標聲源輻射頻率為[160 Hz,200 Hz]寬帶信號，背景噪聲為高斯白噪聲，各傳感器拾取數據所含信噪比為SNR。仿真掃描平面為水平距離[20 m,200 m]、方位角度[-90°,90°]，將該區域按掃描網格劃分，網格間距為2 m，角度1°。

圖 5—圖 8分別給出了4種方法在SNR=-10 dB情況下所得聲圖；圖9給出了4種方法在SNR=-10 dB情況下所得距離R=80 m處不同角度下聲圖測量值。

由圖5—圖9顯示結果可得不同方法輸出最大旁瓣級如表2所示。

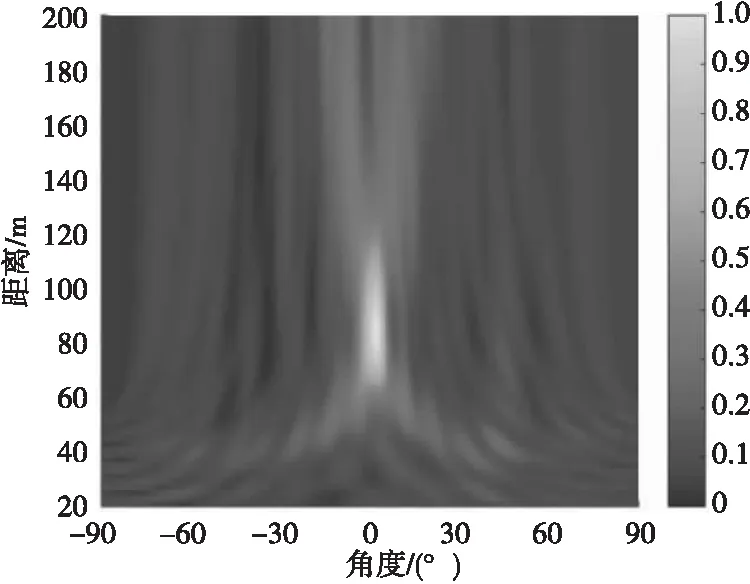
圖5 CBF方法所得聲圖Fig.5 Two-dimensional source distribution map of CBF method

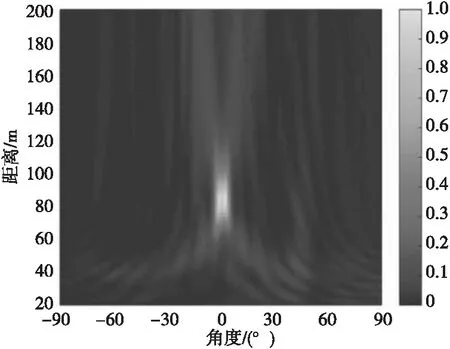
圖6 MVDR方法所得聲圖Fig.6 Two-dimensional source distribution map of MVDR method

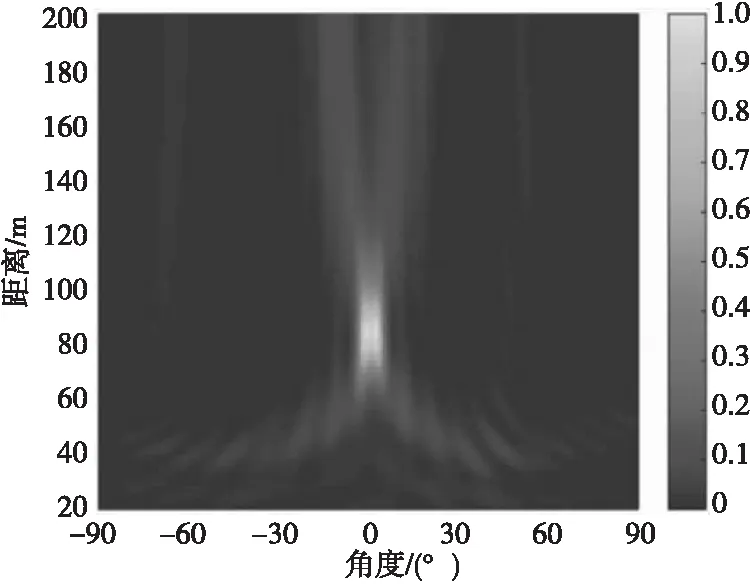
圖7 文獻[11]方法所得聲圖Fig.7 Two-dimensional source distribution map of Ref.11 method

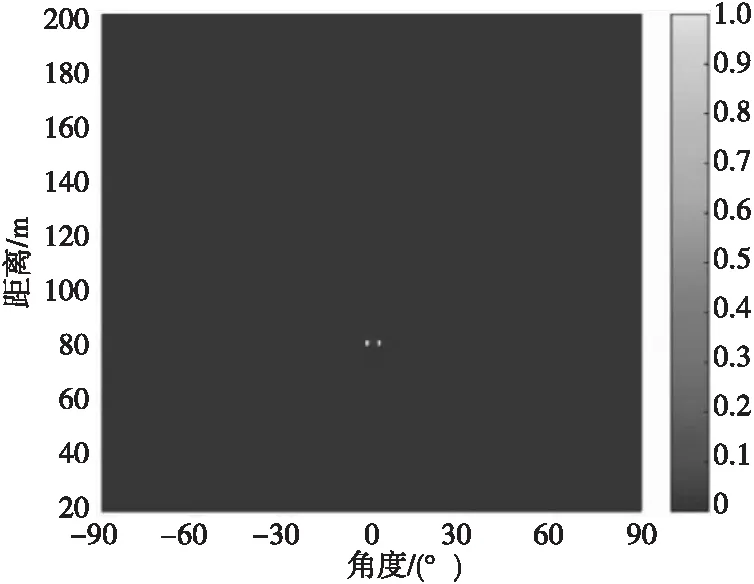
圖8 DMVDR方法所得二維聲圖 (I=6)Fig.8 Two-dimensional source distribution map of DMVDR method(I=6)

表2 不同方法輸出最大旁瓣級Tab.2 The output max side valve of different methods

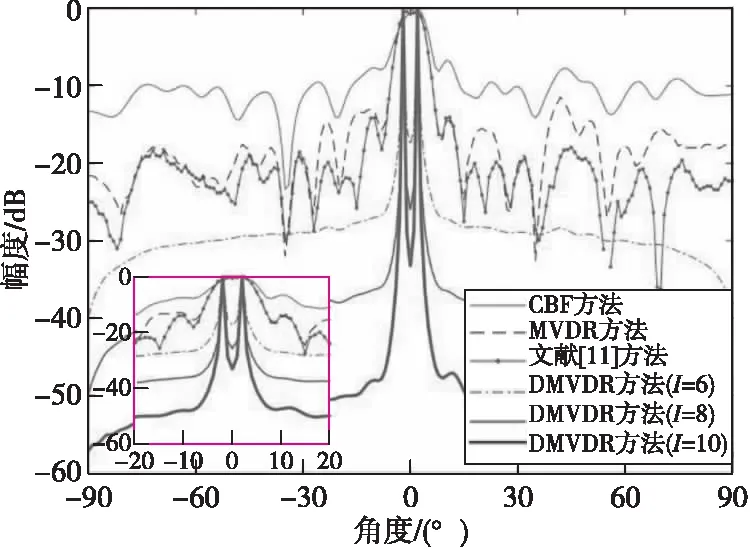
圖9 4種方法所得一維聲圖Fig.9 One-dimensional source distribution map of four methods

由表2可知：DMVDR方法輸出最大旁瓣級變化趨勢與其輸出背景級一致，隨著I變大，其輸出最大旁瓣級降低越大，進一步說明該方法降低的旁瓣級可使其背景更為光滑，目標顯示更為清晰，可降低對其他目標的影響，便于真實目位置提取。

不同方法輸出聚焦峰尺度如表3所示。

表3 不同方法輸出聚焦峰尺度Tab.3 The output focus peak scales of different methods

由表3可知：CBF方法受“瑞利限”限制，所得聲圖聚焦峰尺度較大，分辨能力較差，當兩目標聲源較近時產生混疊現象；MVDR方法和文獻[11]方法通過對目標和非目標進行約束處理，降低了聚焦峰尺度，目標位置分辨率得到提高，減小了“混疊”影響，能夠分辨出兩個目標空間位置，但顯示清晰度有限；而DMVDR方法通過多次迭代解卷積運算即可實現優于MVDR方法和文獻[11]方法的效果，且隨著I變大，其輸出峰值更“尖銳”，聚焦峰尺度越小，目標位置分辨率越好，能夠更清晰地顯示出兩目標聲源位置。該結果進一步說明DMVDR方法輸出聲圖繼承了MVDR方法的高分辨估計性能，能更優地估計出目標位置。

4 結論

針對最小方差無畸變響應聲圖測量方法輸出聲圖背景級較高問題，本文提出一種基于圖像復原處理的近場MVDR聲圖測量方法——DMVDR方法。DMVDR方法通過MVDR方法輸出聲圖所包含的信息對其處理中的點擴展函數實現設計，并基于圖像復原理論中解卷積技術實現對MVDR方法輸出聲圖進行解卷積，減少了背景級對其輸出結果的影響，對目標聲源實現了空間位置分布估計。數值仿真結果表明：DMVDR方法通過解卷積迭代處理有效降低了聲圖背景級，使其低于CBF方法、MVDR方法、文獻[11]方法輸出聲圖背景級，背景更加平滑，聲圖峰值更加“尖銳”，顯示效果清晰可辨，并具有與MVDR方法一致的目標聲源空間位置高分辨估計能力和空間位置分布估計能力。