最小工作時長約束下的傳感器調度方法
安 雷,李召瑞,吉 兵,陳志剛
(1.陸軍工程大學石家莊校區,河北 石家莊 050003;2.中國人民解放軍32272部隊,甘肅 蘭州 733000)
0 引言
傳感器調度主要通過有針對性地分配傳感器資源及探測時間區間,以達到提升目標跟蹤精度、增強系統生存能力、擴大偵測覆蓋范圍及優化信號處理效果等改善傳感器系統性能的目的[1]。根據決策時長可將調度方法分為短時調度和長時調度,短時調度方法以單步收益為決策依據,系統設計簡單、計算量小[2];而長時調度方法考慮多步累計收益,雖然增加了一定計算量,但優化性能要明顯優于短時調度[3-4]。不過,由于兩類方法均未對單個傳感器的工作時間進行約束,導致存在因頻繁切換而使系統響應延遲大量累積,進而降低目標跟蹤精度的問題[5]。
為此,在確保跟蹤精度的同時,必須充分考慮降低傳感器頻繁切換所帶來的使用代價即切換代價的問題。文獻[6—7]將交接次數閾值代入到調度方案求解當中,但獲得的結果并不穩定。文獻[8]為應對相控陣雷達跟蹤中存在的時延問題,引入調度代價以確保任務優先級,但可操作性不強,容易丟失最優解。文獻[9—10]則對傳感器每次執行觀測任務的時長進行了約束,若當前傳感器完成了此輪觀測,則立即擇優選取其他傳感器執行任務,由于該方法放棄了過多的可選方案,導致調度效果明顯欠佳。而文獻[11—12]雖然同樣對傳感器每次執行任務的時長進行了約束,但規定了達到基本時長后,仍可依據下步預測結果繼續調用當前傳感器,保留了更多可選方案,優化效果更好。
針對上述問題,本文以理想條件下的多傳感器多目標跟蹤為應用場景,借助經典目標跟蹤濾波算法,提出基于切換代價控制的最小工作時長約束調度方法。
1 問題的數學模型
在傳感器對目標的實際跟蹤中,由于量測結果常常存在包含噪聲、目標漏檢以及虛警等問題,因此普遍基于部分可觀馬爾可夫決策過程(partially observed MDP, POMDP)對傳感器調度過程進行建模[13]。其基本流程:系統執行上一時刻得到的調度動作,由相應傳感器工作一定時長,獲得目標狀態的量測結果;將量測結果代入調度方法,并依據優化目標得到下一時刻調度動作,如此循環往復[3]。
1.1 調度動作
規定系統中有N部主動傳感器,觀測區域內存在M個敵方目標,且當前為k時刻,則調度動作可定義為:
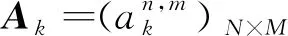
(1)
式(1)中,
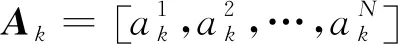
(2)
1.2 目標狀態模型
由于觀測區域內共有M個目標,所以k時刻的多目標狀態模型為:
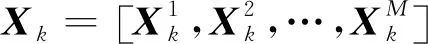
(3)
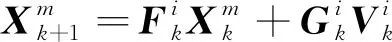
(4)
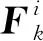
1.3 目標量測模型
(5)
1.4 目標優化函數
充分考慮不同傳感器功能的差異性,將傳感器n的最小工作時長設為φn。假設傳感器n1在k時刻已工作滿φn1時長,則此時依據目標優化函數決策是否進行切換,其中n1按照單步時長確定決策依據,其余傳感器則按照最小工作時長φn確定決策依據。在此基礎上,構建最小工作時長約束調度目標優化函數
(6)
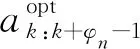
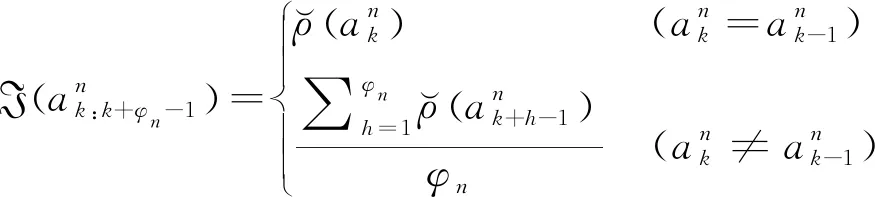
(7)
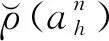
2 傳感器調度方法
2.1 IMM-FQPF濾波算法
結合前文對目標狀態模型和目標量測模型的定義,本文采取基于交互式多模型(interacting multiple model,IMM)[14-15]的濾波算法進行目標狀態估計。同時,由于模糊積分粒子濾波(fuzzy quadrature particle filter,FQPF)[16]相比于粒子濾波所具備的并行處理能力和更佳的濾波性能,為更好地實現多目標跟蹤濾波,提出IMM-FQPF濾波算法。
步驟1 初始數據交互
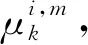
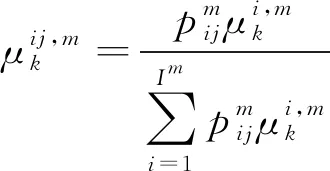
(8)

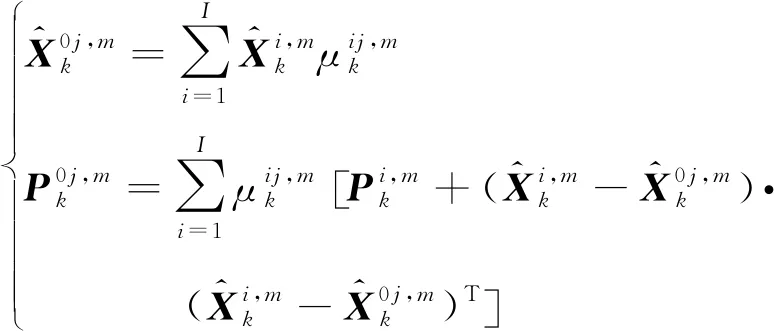
(9)
步驟2 模型濾波估計
1) 狀態估計及其協方差矩陣
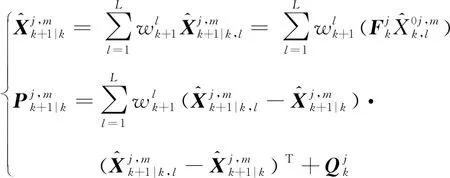
(10)
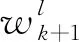
2) 模型殘差及其協方差矩陣
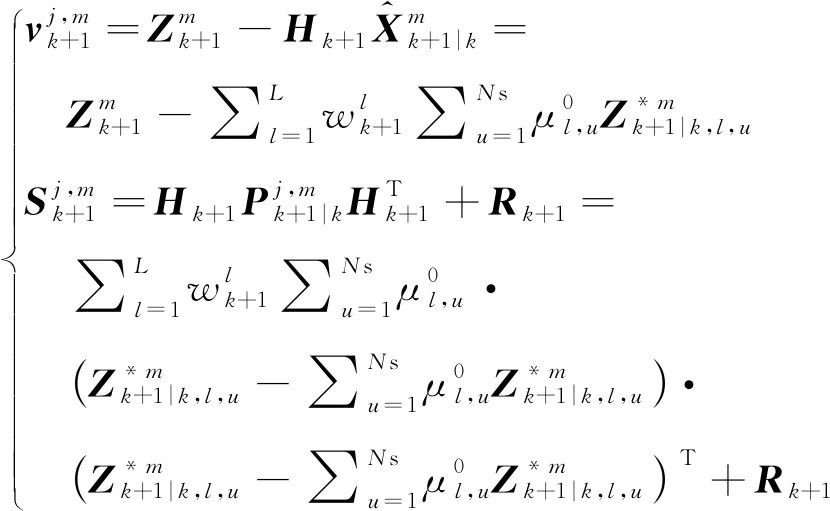
(11)
式(11)中,NS為粒子數目,且有
則為粒子u的權值。
3) 狀態估計及其協方差矩陣
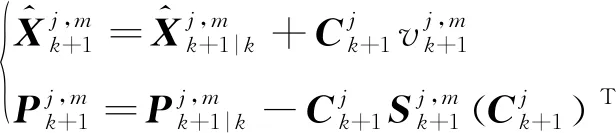
(12)
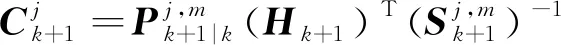
(13)
步驟3 模型概率更新
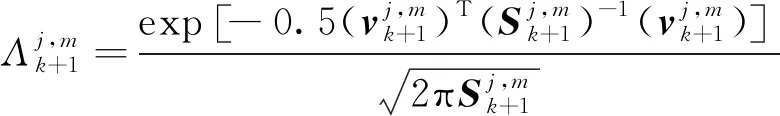
(14)
且模型j的模型概率更新為:
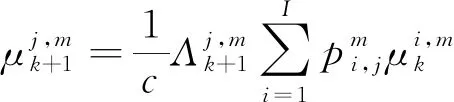
(15)
式(15)中,c為歸一化因子,
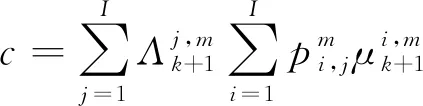
(16)
步驟4 數據估計融合
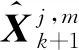
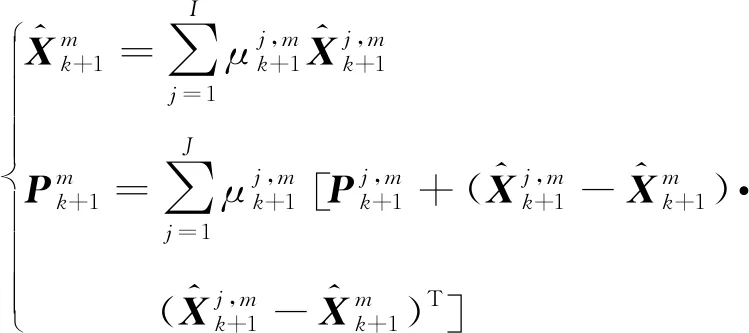
(17)
2.2 基于PCRLB的目標跟蹤精度預測方法
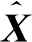
步驟1 初始化
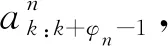
步驟2 獲取狀態轉移矩陣
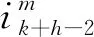

(18)
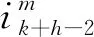
步驟3 計算目標狀態預測值
步驟4 計算目標量測預測值
步驟5 代入IMM-FQPF濾波算法
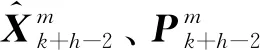
步驟6 定義Fisher信息矩陣
由于目標估計狀態預測值滿足:
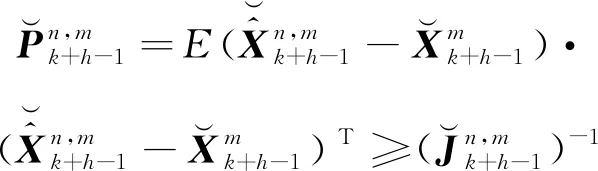
(19)
故Fisher信息矩陣可定義為:
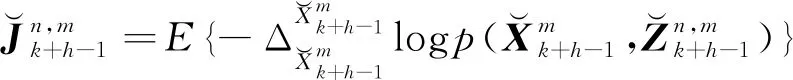
(20)
步驟7 獲取目標運動狀態模型
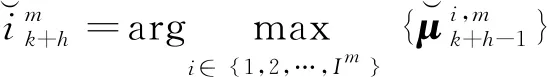
(21)
步驟8 計算目標狀態轉移先驗概率密度函數
依據文獻[20],目標m的狀態轉移先驗概率密度函數為:
(22)
步驟9 計算Fisher信息矩陣

(23)
式(23)中,

(24)
步驟10 計算跟蹤精度預測值
本文考慮理想條件下的多目標跟蹤背景,所以采取將多目標跟蹤分解成多個單目標跟蹤的方式來實現,傳感器n針對目標m的跟蹤精度預測值為:
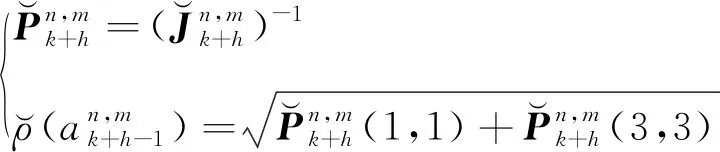
(25)
則傳感器n針對多目標的跟蹤精度預測值為:
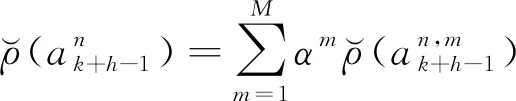
(26)
式(26)中,αm為傳感器系統在跟蹤目標時根據其威脅程度分配的權重系數。
步驟11 循環
若h<φn,令h=h+1,轉到步驟2;若h=φn,循環結束,計算傳感器n在最小工作時長φn內的長時跟蹤精度預測值:
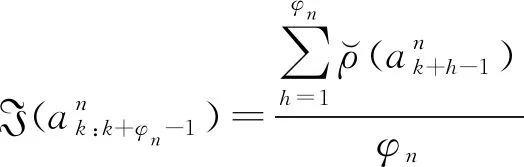
(27)
2.3 調度方法及流程
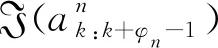
步驟1 初始時刻
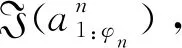
步驟2 重新決策
若k時刻(k>1)傳感器n1已達到最小工作時長要求,則重新進行決策。
步驟3 預測目標跟蹤精度
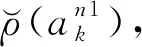
步驟4 決策選取調度方案
將各傳感器跟蹤精度預測值代入目標優化函數式(6)中,決策選取最優傳感器η。
若η=n1,則k時刻繼續調用傳感器n1工作,工作時長h=1。
若η≠n1,則k時刻切換傳感器η工作,工作時長h=φη。
步驟5 執行調度方案
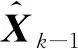
步驟6 循環
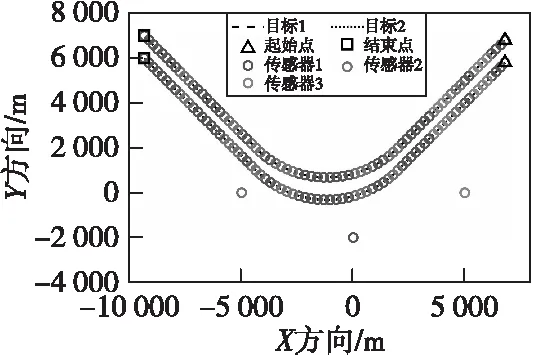
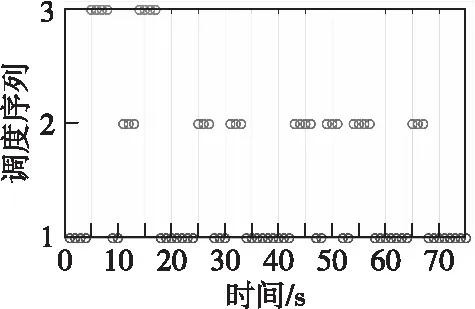
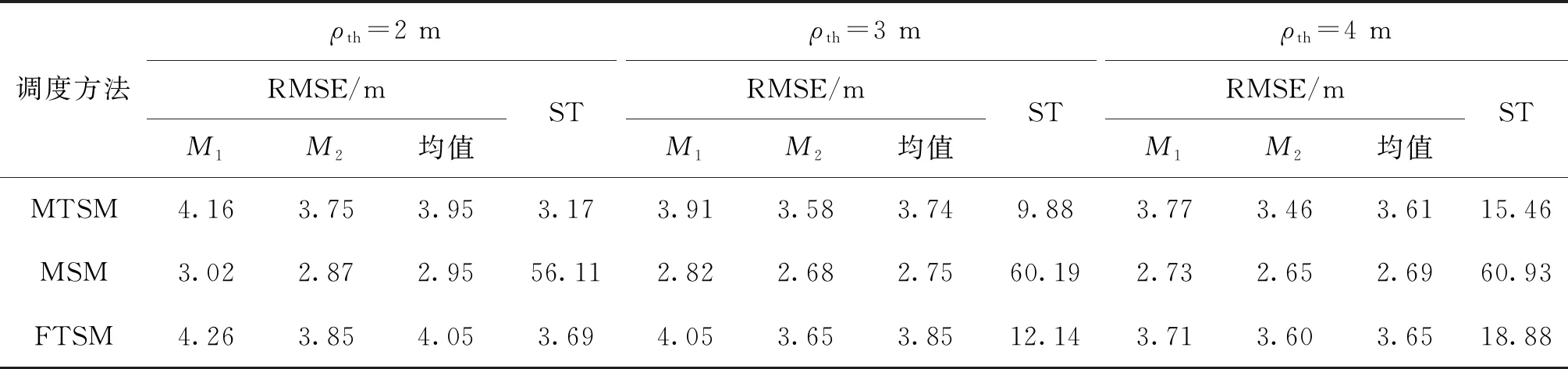
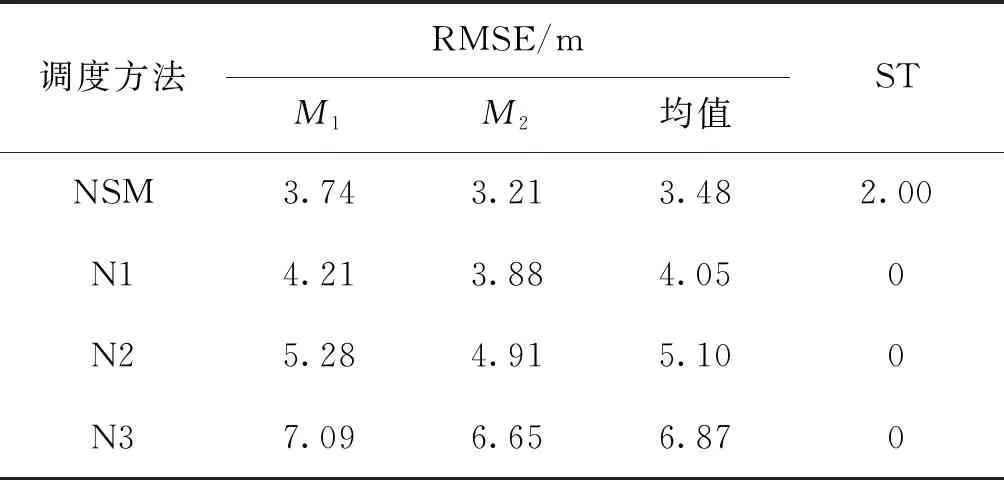
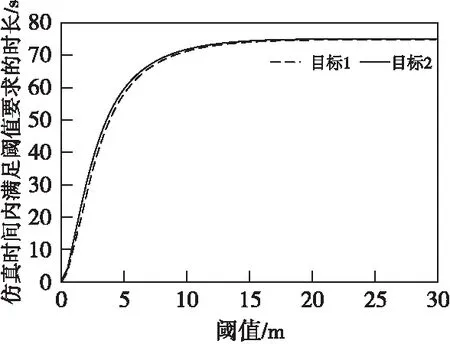
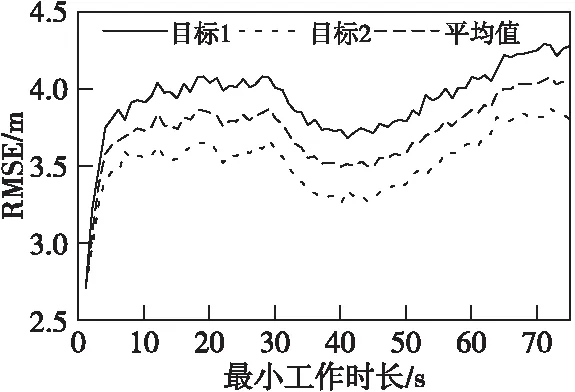
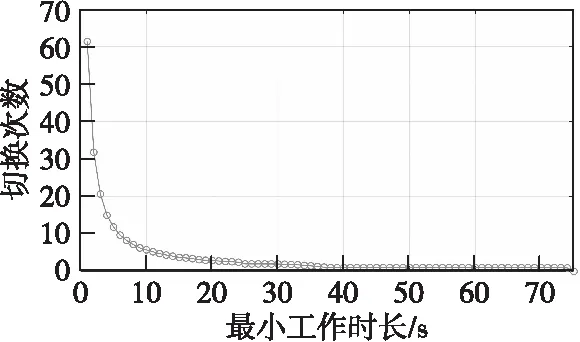
若k+h-1 若k+h-1≥H,則調度任務結束。 調度方法流程如圖1所示。 圖1 最小工作時長約束調度方法流程圖Fig.1 Flow chart ofminimum working timestep constrained scheduling method 假設系統采樣間隔τ=1 s,且包含3臺主動傳感器,跟蹤2個機動目標,傳感器的位置分別為N1(0 m,-2 000 m),N2(-5 000 m,0 m),N3(5 000 m, 0 m),量測噪聲協方差矩陣分別為R1=diag([0.5 m;10-6rad]),R2=diag([1 m;2×10-6rad]),R3=diag([1.5 m;3×10-6rad])。由于探測性能越好的傳感器向外輻射電磁波的能力越強,為提高傳感器系統戰場生存能力,盡可能地避免被敵方截獲探測信號,規定探測性能越好的傳感器最小工作時間φ越短,則各傳感器最小工作時長分別設置為φ1=2 s,φ2=3 s,φ3=4 s,跟蹤任務時長75 s。 在仿真中,為驗證提出的基于切換代價控制的最小工作時長約束調度方法(minimum working timestep constrained scheduling method, MTSM),同時與基于目標跟蹤精度最優化的短時調度方法(myopic scheduling method, MSM)[7]和就近調度方法(nearby scheduling method, NSM)[11]、固定時長調度方法(fixed time scheduling method, FTSM)[9]以及單傳感器跟蹤進行對比。 為較為直觀地顯示調度方法對傳感器切換代價的控制作用,采取仿真時間內傳感器系統的切換次數(switching times, ST)作為切換代價的評價指標,并以任務時間內目標估計狀態的均方根誤差均值(root mean square error, RMSE)作為目標跟蹤精度的評價指標,為便于表述,后文中以“RMSE”代表任務時間內的均方根誤差均值。在目標跟蹤精度閾值ρth=4 m時,利用本文所提MTSM進行調度,得到目標運動軌跡如圖2所示,傳感器調度序列如圖3所示。 圖2 目標運動軌跡Fig.2 The targetmotion trajectory 圖3 傳感器調度序列Fig.3 Sensor scheduling sequence 圖4所示為本文所提的MTSM與MSM、FTSM在不同閾值條件下,以及NSM、各傳感器單獨工作時,仿真時間內各時刻目標估計狀態的均方根誤差對比情況。 圖4 各時刻目標估計狀態均方根誤差對比Fig.4 Comparison of root mean square error of target estimation state at each time 相同實驗中的RMSE及ST對比情況如表1、2所示。 從表2中可知,在使用單傳感器實施目標跟蹤時,由于不進行優化選取,跟蹤全程都采取同一傳感器,導致跟蹤精度較低,與應用各調度方法得到的跟蹤結果相比存在較大的差距。 表1 閾值可調節調度方法的性能對比Tab.1 Performance comparison of threshold adjustable scheduling methods 而相比于MSM的短時調度方法,MTSM在跟蹤精度上稍差,在表1中的3個閾值條件下,得到的RMSE均高于MSM,但傳感器切換次數ST則要遠低于MSM。由于MTSM的優化目標是在一定跟蹤精度的基礎上,有效降低傳感器切換代價,所以MSM在切換代價上的巨大差距使得其跟蹤精度優勢并不明顯,無法滿足切換代價優化的要求。 同時,對比FTSM工作滿固定時長后即切換其他傳感器的情況,本文所提MTSM規定傳感器在工作滿最小時長后,再依據決策指標決定是否切換,保留了更多的可行解,所以得到的調度方案更優。在表1中,MTSM在3個閾值條件下,無論是RMSE還是ST,均要優于FTSM。 表2 NSM調度及各傳感器單獨工作時的性能對比Tab.2 Performance comparison of NSM scheduling and each sensor working alone 結合表1和2可知,僅基于傳感器和目標間距離進行調度的NSM得到的RMSE要優于本文所提MTSM,高于短時調度MSM。但由于影響跟蹤精度的約束條件不僅只有距離,還必須考慮傳感器的探測性能,所以,NSM的原理與實際情況不符,在傳感器調度中并不適用。 仿真可知,相較于其他調度方法以及單傳感器目標跟蹤,MTSM能夠在保證跟蹤精度的基礎上,實現對傳感器切換代價的高效控制,更加符合實際跟蹤情況,具備一定的優勢。 從表1中可知,隨著目標跟蹤精度閾值的增加,本文所提MTSM調度得到的RMSE和ST發生了明顯變化,為進一步分析閾值ρth對MTSM調度性能的影響,在[0 m,30 m]區間內間隔0.5 m采樣,進行仿真實驗與分析,其余參數設置不變。如圖5所示為不同跟蹤精度閾值條件下,采取MTSM進行調度所得到的RMSE和ST變化情況,圖6則為仿真時間內滿足閾值要求的采樣時刻數。 從圖5可知,隨著跟蹤精度閾值的增加,RMSE先增大再減小后保持平穩,而ST先減小再增大后保持平穩。同時,在閾值ρth≥7 m時,RMSE及ST開始趨于穩定,且ρth在區間[7 m,30 m]內的平均RMSE=3.44 m,平均ST=20.86,而ρth=0 m時RMSE=3.45 m,ST=21.40,可見在ρth=0 m及ρth≥7 m時,MTSM的調度性能基本相同。 圖5 不同跟蹤精度閾值條件下MTSM的調度性能Fig.5 Scheduling performance of MTSM under different tracking accuracy thresholds 圖6 不同跟蹤精度閾值條件下任務時間內滿足閾值要求的時長Fig.6 Time to meet threshold requirements within the mission time under different tracking accuracy thresholds 而當ρth在 (0 m,7 m)區間內時,由于閾值的限制,MTSM在調度中出現舍去可行解的情況,并隨著ρth的增大,出現該情況的時刻相應增多,導致RMSE增大,但當ρth增加到1.5 m時,從圖5可知,此時RMSE=4.01 m,ST=1.24,且通過仿真可知調度序列中傳感器1的占比達到了96.51%,說明在ρth≤1.5 m時,閾值的限制作用會隨著ρth的增大而增強,逐漸舍去了傳感器2和傳感器3,導致調度效果變差;而在ρth≥1.5 m時,跟蹤精度滿足閾值要求的時刻逐漸增多,閾值限制作用減弱,調度效果得到改善。 因此,可以通過調整跟蹤精度閾值,實現對目標跟蹤精度和傳感器切換代價的有效控制。在本文仿真條件下,建議跟蹤精度閾值可以在區間[1.5 m, 7 m]內選取。 由于本文所提MTSM的長時屬性是由最小工作時長φ所賦予的,為進一步分析研究φ對調度性能的影響,分別在[1 s,75 s]區間內按照系統采樣時間間隔1 s對φ進行取值,開展仿真實驗。為便于對結果進行分析比較,設定3臺傳感器的最小工作時長相同。同時通過3.2節仿真可知,閾值會對調度性能產生較大影響,為確保實驗的準確性,規定ρth=0 m,以隔絕跟蹤精度閾值干擾。不同最小工作時長下MTSM調度得到RMSE和ST對比情況如圖7、圖8所示。 圖7 不同最小工作時長下MTSM調度得到的RMSEFig.7 RMSE obtained by MTSM under different minimum working timestep 圖8 不同最小工作時長下MTSM調度得到的STFig.8 ST obtained by MTSM under different minimum working timestep 從圖7可知,隨著最小工作時長φ的增加,RMSE先是逐漸增大,隨后由于傳感器位置和性能、目標運動軌跡等仿真條件的限制,以及噪聲干擾等多種因素的綜合作用,在[10 s,44 s]區間內表現出先平穩再降低再平穩的趨勢。 當φ≥44 s之后,RMSE又逐漸增大,結合圖4(d)和表2分析原因,隨著φ的進一步增加,初始時刻決策得到的最優傳感器將固定為單獨跟蹤時RMSE最低的M1,但由于其在44 s之后的局部跟蹤精度低于M2,所以隨著φ的增加,M1的工作時間增加,M2的工作時間減少,導致RMSE增大,直至φ=75 s時,調度序列全部為M1,得到的RMSE和ST與M1單獨工作時的一致。 本文仿真條件下,為在降低切換代價的同時,避免單個傳感器長時間的工作,結合圖7和圖8,建議最小工作時長φ在區間[2 s,9 s]內選取。 本文以多傳感器跟蹤多目標為應用場景,利用IMM-FQPF濾波算法和PCRLB實現目標跟蹤精度預測,引入最小工作時長約束策略,提出切換代價控制的調度方法MTSM。仿真實驗表明,所提最小工作時長約束調度方法MTSM跟蹤效果穩定,在保證一定目標跟蹤精度的基礎上,有效降低了傳感器切換代價;同時,可依據實際任務需求,通過改變目標跟蹤精度閾值和最小工作時長的大小,對調度方法的優化性能進行調整,最后給出了目標跟蹤精度閾值和最小工作時長的取值建議。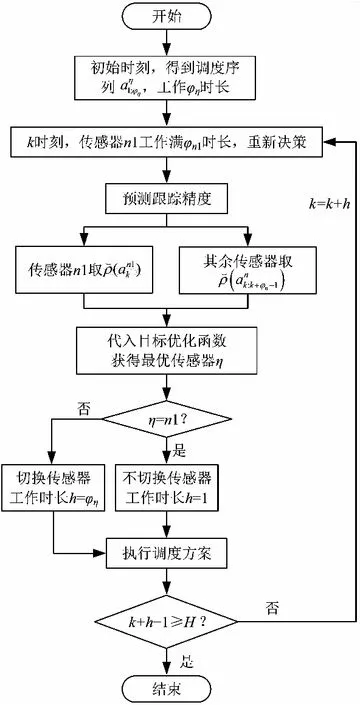
3 仿真驗證與分析
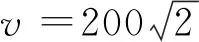
3.1 調度方法性能分析
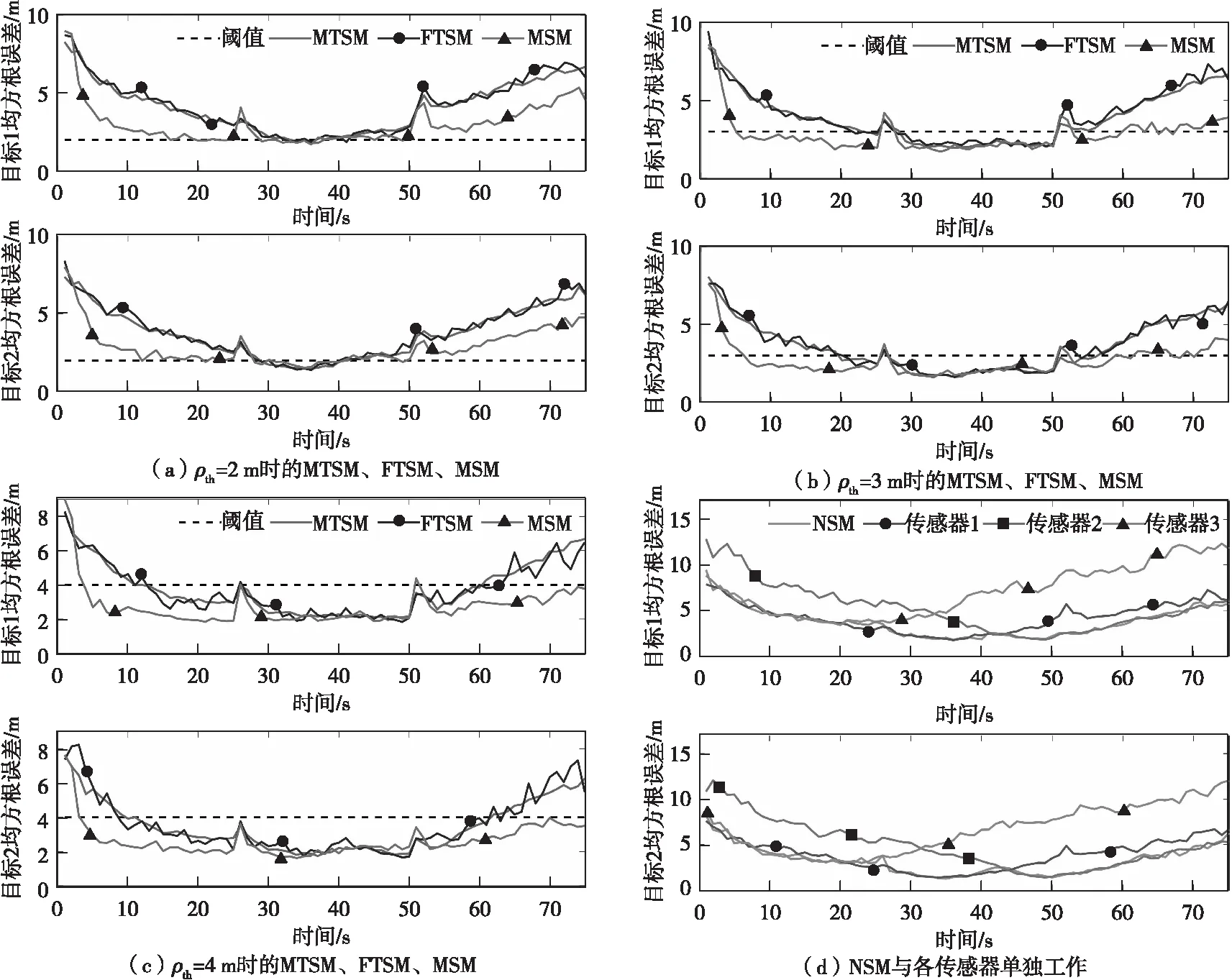
3.2 目標跟蹤精度閾值對調度性能的影響
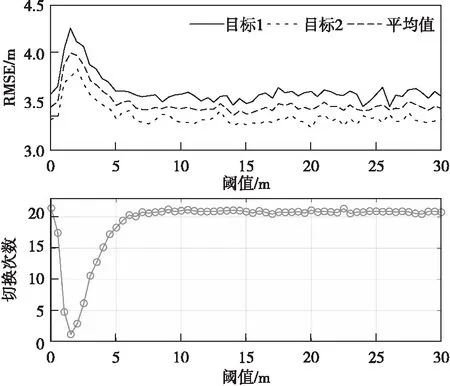
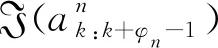
3.3 最小工作時長對調度性能的影響
4 結論

