粗糙元對零攻角尖錐模型高超聲速邊界層轉捩的影響研究

成江逸，司馬學昊，吳 杰

（華中科技大學航空航天學院，武漢 430074）

臨近空間高超聲速飛行器是當前的研究熱點，其具有機動性高、飛行軌跡難以捕捉及預測等特點。但是，較之常規彈道式高超聲速飛行器，臨近空間飛行器飛行的高度低、空氣密度大，隨之而來的便是飛行器熱防護問題。高超聲速飛行器在大氣層內以高超聲速飛行時湍流邊界層的熱負荷與摩擦阻力可達層流邊界層的3～5 倍［1］。因此，維持高超聲速飛行器表面的層流區域是高超聲速飛行器降熱減阻的重要途經之一。高超聲速邊界層轉捩分為主動控制與被動控制。主動控制方法需要向流動施加能量，目前有壁面吹吸以及等離子激勵等，但由于其對應的控制機構復雜，在飛行工況下能量輸入需求大，效用相對較低。相較于主動控制技術，被動控制技術機構簡單、無需能量輸入，容易在飛行器上實現，常用邊界層轉捩被動控制方法包括超聲波吸收材料、波紋壁、槽道以及粗糙元等［2］。在諸多邊界層轉捩被動控制手段中，粗糙元通常會促進高超聲速邊界層轉捩，并定義，臨界粗糙元為開始影響層流轉捩的粗糙元大小，有效粗糙元為立即引起層流轉捩的粗糙元大小［3］。早在1959 年James［4］在帶粗糙元條帶的空心圓柱自由飛行實驗中發現了邊界層轉捩延遲現象。1964 年，Holloway 與Sterrett［5］在風洞平板實驗中發現在特定粗糙元及一定來流情況下，轉捩起始點被延遲。2006年，Fujii［6］在Ma7.1尖錐實驗中發現粗糙元延遲轉捩起始點，且還發現微波浪紋壁與等效三維球體粗糙元效果相同，轉捩起始點與流場波動譜差別不大。

近期Zhong［7-21］團隊開展了大量粗糙元對高超聲速邊界層不穩定性的研究工作。2010 年，Duan等［7］在驗證高階切割單元數值模擬時，偶然發現表面粗糙元延遲了平板層流邊界層轉捩起始點。而后，他們接著使用直接數值模擬探究了粗糙元高度、粗糙元位置、粗糙元寬度、多粗糙元及間距等粗糙元各參數對邊界層轉捩的影響。研究發現，粗糙元只有在位于特定第二模態不穩定波的同步點下游時才可能延遲邊界層轉捩，其次還發現低于當地邊界層高度的粗糙元延遲了邊界層轉捩，并且粗糙元高度越高，抑制無量綱壓力幅值效果越好［7-12，16］。粗糙元寬度未展現明顯效果［13，16］。多粗糙元研究結果表明，當粗糙元間距為10 倍粗糙元寬度左右時，多粗糙元抑制無量綱壓力幅值效果最好，且多粗糙元效果優于單粗糙元效果［13，16］。Mortensen 和Zhong［12］還考慮真實氣體模型以及熱化學非平衡，通過數值模擬發現，相較于理想氣體模型，粗糙元對第二模態不穩定波幅值的抑制效果在真實氣體模型里更有效。在高超聲速邊界層轉捩中，Mack第二模態不穩定波占主導作用［22-23］。由于粗糙元的存在，會在邊界層內，粗糙元前后產生分離區。在流動分離區附近的第二模態不穩定波無法進入分離區，只能在聲線與分離區之間的被分離區壓縮了的區域反射傳播［24］。通過Miles 定律，這種反射會導致幅值降低，從而抑制了第二模態不穩定波發展。Haley 和Zhong［17］認為抑制作用程度大小取決于分離區大小，在數值模擬帶粗糙元尖錐情況下，后分離區大小明顯小于平板粗糙元后分離區大小，但其對第二模態不穩定波的抑制作用仍可與平板情況下的相比較。由于可能是數值模擬計算二維平板與三維尖錐所帶來對分離區大小相差較大的問題，因此認為分離區對第二模態不穩定波的影響仍然有待探究。國內周云龍［25］使用直接數值模擬方法研究了粗糙元3 種外形對流場的影響，發現矩形粗糙元抑制效果最好。

現階段在探究粗糙元對高超聲速邊界層影響時，主要使用直接數值模擬方法，加入的擾動頻率單一。但自由來流情況下，來流擾動的頻率呈離散式分布；并且，數值模擬的邊界條件設定也往往與風洞實驗存在差異。因此，僅依靠數值模擬方法探究粗糙元對邊界層轉捩的影響仍存在較大難度。針對以上問題，本實驗研究嘗試探究粗糙元對邊界層不穩定波發展以及轉捩過程的影響。

1 實驗平臺與實驗模型

1.1 實驗平臺

本次風洞實驗依托華中科技大學Φ0.25 mMa6 Ludwieg 管風洞［26］，如圖1 所示。該Ludwieg管風洞由雙U 形高壓長直儲氣段、快開閥、Laval 噴管、實驗段、擴張段以及真空罐等主要部件組成。風洞的高壓儲氣段與Laval 噴管通過快速控制閥門分開。在風洞啟動前，儲氣段內儲存著高溫高壓空氣，控制閥門下游的部分則通過真空泵抽成了真空。在開啟快速控制閥門的瞬間，會產生一系列的非定常膨脹波，該膨脹波以聲速向儲氣段的上游行進；該膨脹波驅動管內的氣體達到儲氣段啟動馬赫數。當膨脹波以當地聲速到達儲氣段尾端后，再次被反射回來。當反射膨脹波到達快速控制閥時，快速控制閥門關閉，風洞的運行結束。與此同時，在快速控制閥的下游，受壓差驅動，氣流在Laval 噴管喉部形成聲速流，并沿著Laval 噴管膨脹加速，在試驗段時獲得對應設計馬赫數的高超聲速氣流［27］。該風洞建設完成于2020 年并試車成功，風洞單車次有效運行時長約116 ms［26］，如圖2 所示儲氣段與實驗壓力測量數據。歸一化Pitot 壓力脈動結果顯示該風洞的流場品質較之不倫瑞克大學HLB 與美國空軍學院HHK-6 風洞更優［26，28］，如圖3 所示。

圖1 Φ0.25 m Ma6 Ludwieg 管風洞[26]Fig.1 Φ0.25 m Ma6 Ludwieg tube wind tunnel[26]

圖2 有效運行時長[26]Fig.2 Effective running time[26]

圖3 歸一化Pitot 壓力脈動均方根值比較[26,28]Fig.3 Comparison of normalized Pitot pressure pulsation RMS values[26,28]

1.2 實驗模型

本次實驗所使用7°半錐角光滑尖錐模型，模型全長0.4 m，尖錐頭部鈍度為50 μm。模型材質為不銹鋼，共分為4 段，表面粗糙度為Ra3.2（壁面法向上的點與壁面基準線之間距離絕對值的算術平均值小于3.2 μm），如圖4 所示。其中數字黑點代表PCB 孔位及相應編號，第一個PCB 孔位距頂部182.6 mm，后面除3 號與靠后的4 號孔位間隔約30 mm，其余均相間24.8 mm（約25 mm）。由于PCB 數量有限，部分PCB 孔位未安裝PCB 而是使用相應尺寸堵頭封閉。

圖4 光滑尖錐模型與粗糙元條帶布置示意圖Fig.4 Smooth sharp cone model and roughness strip layout

在粗糙元布置方法上，本文借鑒了Fong［16］在裙錐上設計粗糙元的方式，在光滑尖錐表面上粘貼一圈固定厚度的粘膠獲得本實驗所使用的粗糙元尖錐模型。實驗所使用的粗糙元寬度與厚度均分別為2 mm 與0.5 mm。本次實驗共有3 處選擇性放置粗糙元條帶，分別用大寫羅馬數字表示，如圖4 所示。Ⅰ處粗糙元條帶位于1 號與2 號孔位中間；Ⅱ處粗糙元條帶位于Ⅰ處粗糙元條帶后方25 mm；Ⅲ處粗糙元條帶位于Ⅱ處粗糙元條帶后方25 mm。

1.3 壓力傳感器

實驗使用的高頻壓力傳感器為PCB132 系列，如圖5 所示，用于測量模型表面的壓力脈動。傳感器的有效動態響應范圍為10～1 000 kHz，量程為345 kPa，可以分辨的最小壓力為7 Pa，傳感器的固有頻率大于1 MHz。本次實驗所使用的PCB 高頻壓力傳感器敏感性系數分別為：160.4、123.0、148.5、135.3、138.9 和143.8 mV/psi。

圖5 PCB132 系列高頻壓力傳感器Fig.5 PCB132 series high frequency pressure sensor

實驗使用數據采集器采集壓力傳感器測得的信號。所有傳感器的輸出信號由Spectrum A/D 卡采集，采集系統垂直分辨率16 bit。依據Nyquist 采樣定理，采樣頻率應為所采集信號最高頻率的2 倍以實現對信號的精確測量，考慮到高超聲速風洞中第二模態不穩定波以及其諧波高達數百千赫，因此實驗對不穩定波采集選取的采樣頻率為3 MHz。

2 實驗結果與分析

2.1 數據后處理方法

通過對PCB 采集所得時域信號進行傅里葉積分變換，獲得頻域信號，即壓力脈動功率譜密度（PSD）；通過對相鄰PCB 采集所得時域信號進行互相關分析，獲得第二模態不穩定波傳播速度；通過對PSD 數據進行處理，獲取增長率數據，具體的增長率計算公式為［29］

式中：αi為增長率，f為頻率，s為兩測點距離，A（f）為頻率為f時的幅值大小。

通過假設在相鄰壓力傳感器（分別位于sj與sj+1）間增長率為常數，所以中點sj+1/2處的增長率為

式中PSD（f）為頻率為f時PSD 數值大小。

2.2 實驗結果分析與討論

2.2.1 單粗糙元條帶對不穩定波發展的影響

本節風洞實驗探究單個粗糙元條帶對第二模態不穩定波發展以及邊界層轉捩的影響，實驗時使用了圖5 所示中的1、2、4、5、6 與8 號孔位安裝PCB，其余孔位安裝孔銷封堵。粗糙元條帶分別單獨布置于Ⅰ處與Ⅲ處。實驗儲氣段總壓7 bar，總溫350 K，來流單位雷諾數Re∞= 10.71× 106m-1。風洞實驗采集數據經傅里葉積分變換處理所得壓強脈動密度功率譜結果如圖6 所示。

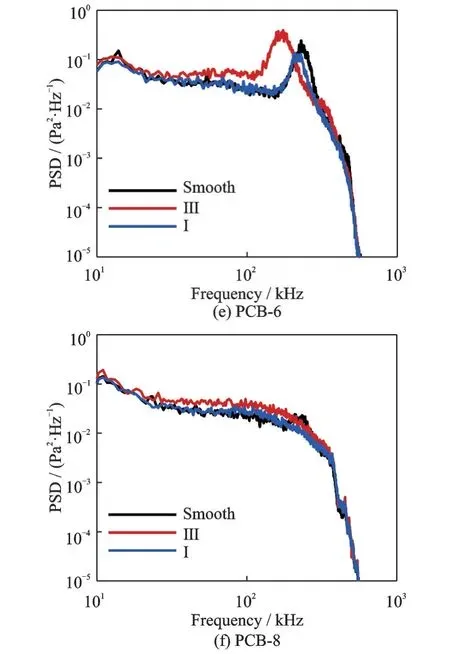
圖6 光滑與單粗糙元條帶尖錐6 個孔位PSD 結果Fig.6 PSD results of pressure fluctuation along sharp cone with smooth surface and single roughness element

由1、2 號孔位PCB 實驗結果可發現，來流在未經過粗糙元時，第二模態不穩定波特征無明顯變化，流場與光滑尖錐保持一致，同時也表明本風洞流場的重復性較好。由2、4 號孔位PCB 實驗結果可發現，剛經過粗糙元的第二模態不穩定波會發生低頻頻移且第二模態不穩定波的最大幅值會有所減小。由4、5、6 號孔位PCB 實驗結果可發現，在經過粗糙元后，第二模態不穩定波的頻移與最大幅值會逐漸趨向于無粗糙元條件下流場結果。同時，也可以發現光滑情況下第二模態不穩定波幅值在5號PCB 孔位附近達到最大并開始衰減，而含粗糙元情況下第二模態不穩定波幅值一直處于增長。可發現粗糙元可延長第二模態不穩定波增長過程。由8 號孔位PCB 實驗結果可發現，第二模態不穩定波經歷了幅值先增大后減小的過程，最終特征消失，僅光滑情況下第二模態不穩定波特征還稍有表現，可判斷粗糙元情況下流動均已湍流，光滑情況下流動即將進入湍流狀態。由此現象可見，粗糙元雖然一定程度上可以降低部分頻率范圍的第二模態不穩定波的幅值，但是其增長率明顯高于光滑尖錐情況。

之后，探究了單粗糙元條帶對第二模態不穩定波傳播速度影響。由于Ⅲ處放置的粗糙元較后，選取的統一對比處為4 號孔位后，由此選擇仍可觀測到第二模態不穩定波信息的4 號與5 號孔位PCB所獲取的信號進行互相關分析，結果如下。如圖7所示為4 與5 號孔位PCB 壓力傳感器信號經過互相關分析得到的曲線。兩個PCB 之間間距為25 mm，在光滑、僅Ⅲ處放置粗糙元與僅Ⅰ處放置粗糙元情況下，兩測點間的時間偏移量分別為0.034 7、0.034 7 與0.035 3 ms。經計算，得到的相速度約分別為720.5、720.5 和708.2 m/s（分別為91.7%、91.7%和90.1%的邊界層外緣速度Ue）。三者差別不大且歸一化相速度均符合［1-1/Ma，1］慢模態相速度區間，說明單粗糙元條帶僅影響了第二模態不穩定波的幅值與增長率，對第二模態不穩定波波包的傳播速度無明顯影響。

圖7 3 種情況下4 與5 號孔位PCB 壓力信號互相關系數曲線Fig.7 PCB pressure signal correlation curves of holes 4 and 5 under three conditions

進一步，對第二模態不穩定波增長率影響進行研究。同樣選取4 號與5 號孔位PCB 所獲取的信號進行分析。如圖8所示為光滑、僅Ⅲ處布置粗糙元與僅Ⅰ處布置粗糙元情況下，4 號與5 號孔位間第二模態不穩定波增長率計算結果。對比光滑與僅Ⅰ處放置粗糙元情況，易發現200 kHz以下頻率增長率幾乎無差別，而200 kHz以上頻率增長率僅Ⅰ處放置粗糙元情況下顯著高于光滑情況；對比光滑與僅Ⅲ處放置粗糙元情況，則100 kHz 以下頻率增長率差別不大，而100 kHz以上是僅Ⅲ處放置粗糙元情況下的增長率先短暫下降后迅速增長起來并大幅超過光滑情況下的增長率。可能是因為Ⅲ處離4、5 號孔位較Ⅰ處更近，顯現出了更為短暫的影響，而顯示的Ⅰ處影響則是隨流場較長時間后的影響或因為是不同位置單粗糙元對不同段頻率有影響，粗糙元越靠后，使受影響最低頻率降低。

圖8 3 種情況下4 與5 號孔位間第二模態不穩定波增長率Fig.8 Amplification rate of the second mode instability wave between holes 4 and 5 under three conditions

2.2.2 多粗糙元條帶對不穩定波發展的影響

本節實驗方法和條件2.2.1 節相同，3 條粗糙元分別位于Ⅰ處、Ⅱ處與Ⅲ處。實驗粗糙元布置方案分別為僅在Ⅰ處放置粗糙元、在Ⅰ處和Ⅱ處放置粗糙元和在3 處均放置粗糙元條帶。實驗數據處理后所獲得的壓強脈動功率譜密度結果如圖9所示。

圖9 光滑與多粗糙元條帶尖錐6 個孔位PSD 結果Fig.9 PSD results of pressure fluctuation along sharp cone with smooth surface and multi-roughness elements

由1、2、4 號孔位PCB 測量結果可知，第二模態不穩定波每經過一次粗糙元條帶，都會發生一次低頻頻移，而最大幅值不變或稍有減小。同樣地，由4、5、6 號孔位PCB 實驗結果可知，第二模態不穩定波經過粗糙元幅值恢復至不放置粗糙元狀態時的位置取決于最后一個粗糙元的位置，越是遠離最后一個粗糙元的位置，第二模態不穩定波越靠近無粗糙元情況下的第二模態不穩定波狀態。由8 號孔位PCB 實驗結果可知，帶粗糙元流動已湍流，光滑情況下流動即將湍流。

探究多粗糙元條帶對第二模態不穩定波傳播速度影響，選取分析段依舊為4 與5 號孔位間，結果如圖10 所示，兩孔位間距25 mm。由圖可知，時間偏 移 分 別 為 0.034 7、0.035 3、0.035 2 和0.034 0 ms。經計算，相速度分別為720.5、708.2、710.2 和735.3 m/s（分別為91.7%、90.1%、90.4%和93.6%的邊界層外緣速度Ue）。4 者差別不大且歸一化相速度均符合［1-1/Ma，1］慢模態相速度區間，說明多個粗糙元條帶對第二模態不穩定波波包的傳播速度依舊沒影響。

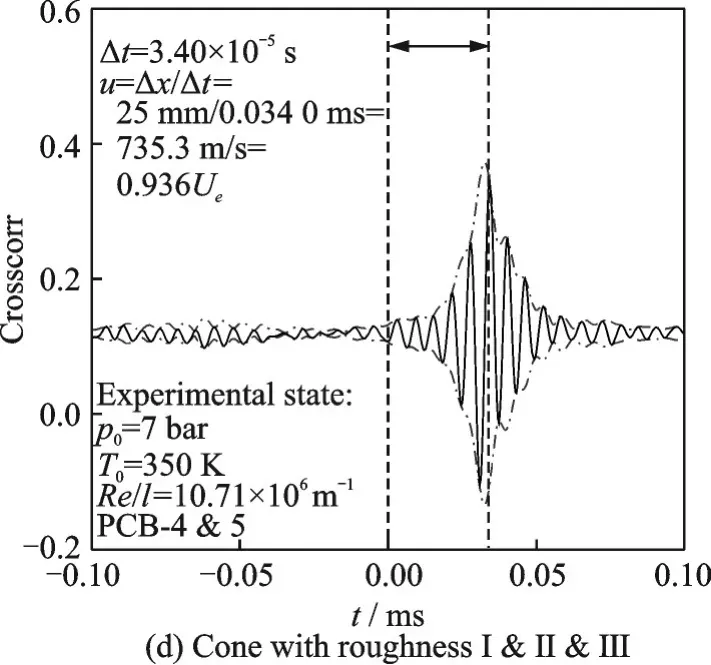
圖10 4 種情況下4 與5 號孔位PCB 壓力信號互相關系數曲線Fig.10 PCB pressure signal correlation curves of holes 4 and 5 under four conditions

之后，研究多粗糙元條帶情況下對第二模態不穩定波增長率影響。同樣選取4 號與5 號孔位PCB 所獲取的信號進行計算，結果如圖11 所示。對比光滑與2 處放置粗糙元情況，易發現120 kHz以下頻率增長率幾乎無差別，而120 kHz 以上頻率增長率先減小后增大并反超光滑情況下增長率大小；對比光滑與3 處放置粗糙元情況，80 kHz 以下頻率增長率與光滑情況下差別不大，而80 kHz 以上增長率先短暫下降后迅速增長并超過光滑情況下的增長率。現象緣由同2.2.1 節，可能增長率也存在與幅值一樣的現象，會恢復至光滑情況下；也可能是粗糙元靠后會使增長率增大的最低頻率減小。

圖11 4 種情況下4 與5 號孔位間第二模態不穩定波增長率Fig.11 Amplification rate of the second mode instability wave between holes 4 and 5 under four conditions

2.2.3 不同來流情況下粗糙元對轉捩影響

為探究不同來流情況下，不同粗糙元布置方法所帶來的效果差異，在總壓7 bar 的基礎上還進行了總壓分別為5 與9 bar，總溫350 K 的實驗，來流單 位 雷 諾 數 分 別 為Re∞= 7.65 × 106m-1與Re∞= 13.77 × 106m-1。粗糙元布置方案分別為僅在Ⅲ處布置粗糙元條帶與在Ⅰ、Ⅱ和Ⅲ處均布置粗糙元條帶。實驗PCB 數據經處理后獲得如圖12所示的功率譜密度圖，其中5 bar 情況下僅選取了6與8 號孔位處，9 bar 情況下僅選取了4、5 與6 號孔位處。

首先對比來流總壓5 bar 情況下PSD 圖。在6號孔位處3 種模型的第二模態不穩定波特征均明顯。但在8 號孔位處，3 處均布置粗糙元條帶情況下的第二模態不穩定波特征即將消失；同時僅Ⅲ處布置粗糙元情況下的第二模態不穩定波特征也不如光滑情況下的明顯。可判斷粗糙元情況下轉捩結束點將被提前。在這兩種粗糙元布置方案中，在5 bar 總壓情況下，3 處均布置粗糙元條帶相較于僅在Ⅲ處布置粗糙元條帶更促進邊界層轉捩結束。圖12（a）中，6 號 孔 位PCB 的PSD 分 布 中 出 現 了300～400 kHz 范圍的次封值頻率可能為第二模態不穩定波的諧波。諧波頻率大致為其主頻的2 倍。此時第二模態不穩定波頻率為140 kHz 和200 kHz左右，而諧波頻率在300 kHz 和400 kHz 左右，正好為第二模態不穩定波頻率的2 倍。由于諧波幅值相較主頻不大，影響不大，因此沒有考慮其影響。

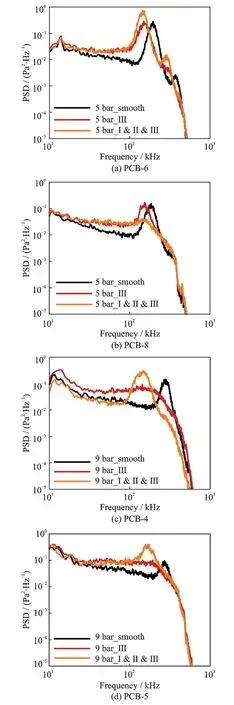
圖12 5 bar 與9 bar 情況下部分孔位PSD 結果Fig.12 PSD results of partial holes at 5 bar and 9 bar

接著對比來流總壓9 bar 情況下PSD 圖。在4號PCB 孔位處，僅在Ⅲ處布置粗糙元情況下的第二模態不穩定波特征已經消失，流動經過粗糙元后立即變成湍流狀態。在5 號PCB 孔位處，在3 處均布置粗糙元與光滑情況下，第二模態不穩定波特征仍存在，但是在6 號PCB 孔位處3 處均布置粗糙元情況下第二模態不穩定波特征消失，流動狀態已經為湍流，而光滑情況下的第二模態不穩定波特征雖不明顯了但是仍然存在，流動即將變成湍流。此時，帶粗糙元條帶情況下流動相較于光滑情況下均提前湍流，并且僅Ⅲ處布置粗糙元條帶相較于3 處均布置粗糙元條帶更促進邊界層轉捩結束。

可以明顯發現，在5 bar 與9 bar 情況下，僅在Ⅲ處布置粗糙元與3 處均布置粗糙元時，不同布置方案對促進邊界層轉捩結束程度的比較結果不同。其原因可能在于不同來流情況下，同步點位置發生了改變。在較低單位來流雷諾數情況下，第二模態不穩定波同步點靠后，3 處均布置粗糙元時靠前的粗糙元條帶可能會起促進轉捩的效果。而在較高單位來流雷諾數情況下，第二模態不穩定波同步點靠前，3 處均布置粗糙元時靠前的粗糙元起延遲轉捩的效果。所以，不同粗糙元布置方案在不同來流情況下效果不同，可見粗糙元布置方案對來流情況較為敏感。

3 結 論

通過風洞實驗探究了不同粗糙元布置方案以及不同來流情況下，粗糙元對第二模態不穩定波以及邊界層轉捩影響。現整理本次實驗探究發現可得出以下結果：

（1）當第二模態不穩定波經過粗糙元時，粗糙元會抑制第二模態不穩定波粗糙元的幅值。但第二模態不穩定波在遠離粗糙元的下游會逐漸恢復至與原光滑無粗糙元情況下的第二模態不穩定波特征。粗糙元雖然會抑制第二模態不穩定波幅值，但會促進第二模態不穩定波頻段的增長率。

（2）從互相關分析結果表明，粗糙元對第二模態不穩定波的傳播速度沒有明顯影響。

（3）粗糙元在局部抑制第二模態不穩定波幅值并且增大其頻段增長率的結果最終表現為促進了轉捩的結束。同時，粗糙元布置方案的效果對來流情況相當敏感。不同來流情況下粗糙元布置方案需改變。