基于隨機森林算法的煤層含氣量三維精細建模*

郭廣山 郭建宏 孫立春 劉麗芳 田永凈

(1.中海油研究總院有限責任公司 北京 100028； 2.油氣資源與勘探技術教育部重點實驗室(長江大學) 湖北武漢 430100)

煤層氣是以吸附態為主的非常規天然氣，歷經幾十年勘探開發實踐，中國已取得顯著成效。2021年全國煤層氣地面抽采達到59.6億m3，已建成沁水盆地南部和鄂爾多斯盆地東緣兩個煤層氣基地。近些年在深部煤層氣、多薄煤層疊置煤層氣藏等領域實現突破性進展。隨著煤層氣勘探開發進程，對煤層氣儲層精細評價和認知深度的需求愈發提高。在諸多煤層氣儲層參數中，含氣性精細評價尤為重要。煤儲層含氣性貫穿于煤層氣開發整個生命周期，從前期煤層氣精準選區、適應性工程工藝設計、探明儲量申報、產能建設以及低產低效井治理對煤層含氣性認識均提出更高的要求。目前，行業內普遍采用參數井直接法確定含氣量大小。為解決含氣性非均質性強等難題，不少學者和專家創新提出諸多含氣量間接方法，如多元回歸分析法、基于測井數據含氣量預測方法、KIM方程含氣量預測方法、地震疊合反演含氣量預測方法、核磁共振技術含氣量預測方法、基于生產數據含氣量預測方法等，這些含氣量間接法有效的提高含氣量的評價精度，適用于不同的勘探開發階段，但受限于煤層氣參數井含氣量測試數量和參與計算數據的準確性[1-3]。隨著大數據、AI技術、機器學習等新技術的興起，不少學者已嘗試將這些技術應用到煤儲層評價中，目前機器學習含氣量預測方法主要包括XGboost算法、隨機森林算法、支持向量機算法和神經網絡算法等[4-8]。煤層氣現場工程工藝迫切需要深化煤儲層含氣量空間分布特征，而三維地質建模在常規油氣儲層方面已得到廣泛的應用，但針對煤儲層參數三維建模應用相對有限[9-14]。同時，未見有將機器學習和三維地質建模有機結合評價煤儲層含氣性。

為解決上述問題，筆者以沁水盆地南部柿莊南高煤階煤層氣田3號煤層為評價對象，依托38口煤層氣參數井含氣量測試數據和476口生產井常規測井資料，利用隨機森林算法建立3號煤層含氣量計算模型，并利用盲井進行可靠性驗證，與實測值吻合度較好。在構建3號煤層構造框架基礎上，利用油氣行業成熟建模軟件構建3號煤層含氣量三維模型，精細刻畫含氣量空間分布規律，為區塊滾動勘探和整體開發奠定基礎。

1 區塊地質概況

柿莊南區塊位于沁水盆地東南部(圖1)，是中國煤層氣勘探程度較高的區塊之一，區塊面積388.0 km2。區域上沁水盆地南部屬于沁水復向斜的南端，整體為一單斜構造。盆地西部主要發育寬緩的 NNE 向的次級褶曲，東部發育近南北向的次級山字形構造，斷層不發育，地層傾角 5°左右，較為平緩。該區塊具有東西分帶的構造格局，整體呈東南高、西北低的構造格局。區內石炭系上統太原組和二疊系下統山西組是主要含煤層系。山西組為一套海陸過渡為主的三角洲沉積體系，其中3號煤層是該區開發目的煤層，煤層厚度分布穩定，主要在4.0～8.0 m，平均6.0 m；中等埋藏深度，主要在400～1 020 m，平均750 m；煤巖成熟度較高，Ro在2.5%～3.0%，為無煙煤三類；參數井注入/壓降試井測試結果顯示3號煤層滲透率整體較低，主要在0.01～0.04 mD，屬特低滲儲層[15-16]。

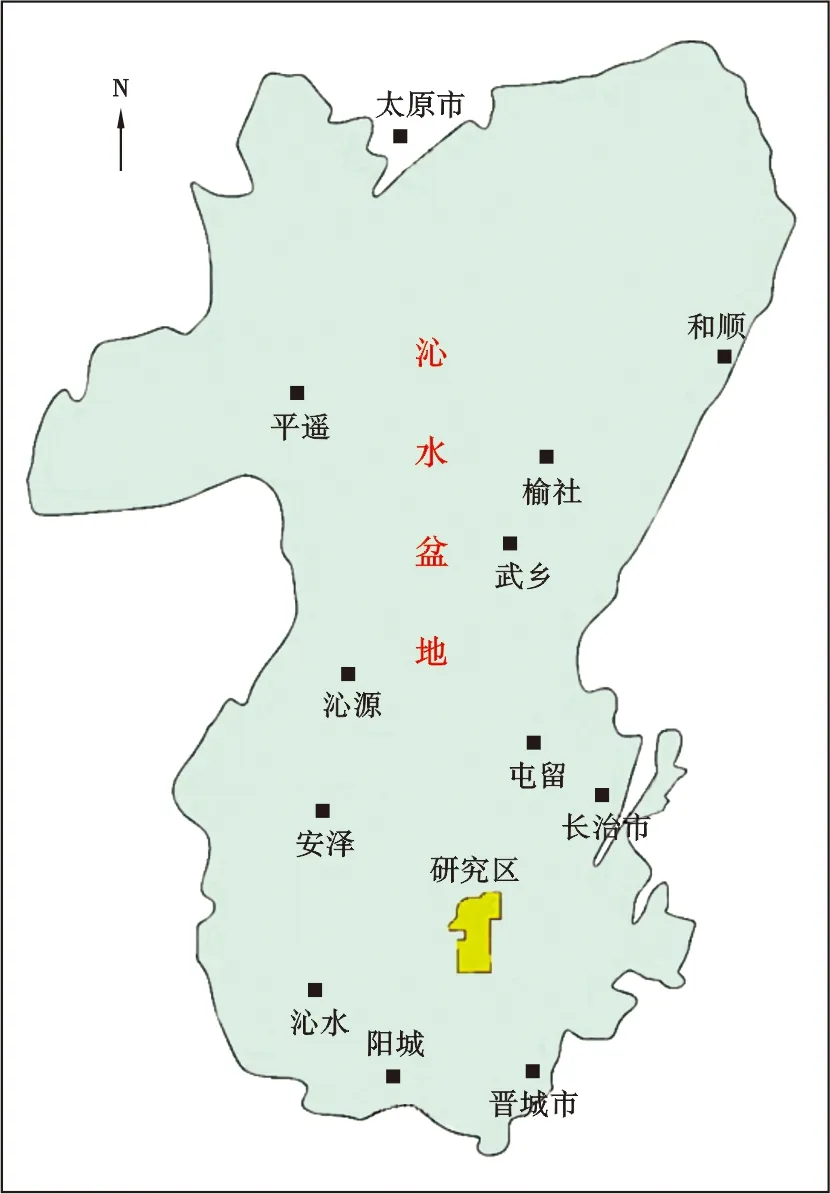
圖1 柿莊南區塊區域位置圖

2 隨機森林算法煤層含氣量預測

2.1 隨機森林方法原理及模型構建步驟

隨機森林算法由Breiman于2001年提出[17]，是一種并行式集成學習方法，即將多個個體學習器組合形成集成模型。隨機森林方法是由同一類型的決策樹模型組成，屬于同質集成。隨機森林算法中的每一個基學習器都是一個決策樹模型。決策樹節點分裂特征選擇指標為Gini指數，相對于信息增益的對數化計算，其計算速度更快。為了防止模型出現過擬合或訓練不充分導致的精度過低問題，將Bagging(bootstrap aggregation)思想引入至隨機森林方法[2]。Bagging是典型的集成學習方法，而集成學習方法的基礎就是Bootstrap方法。Bootstrap是一種抽樣方法，其核心是對一整體樣本進行有放回的抽取，該方法在數據分析中得到了較好的應用[3]。Bagging是基于bootstrap方法的并行式集成方法，所謂并行式方法是指個體學習器之間相互獨立，不存在強依賴關系，可同時生成，即累積多個個體學習器的學習能力，能獲得更優越的泛化性能，提高整體模型的預測精度和穩定性[17]。Bagging算法的流程如圖2所示。

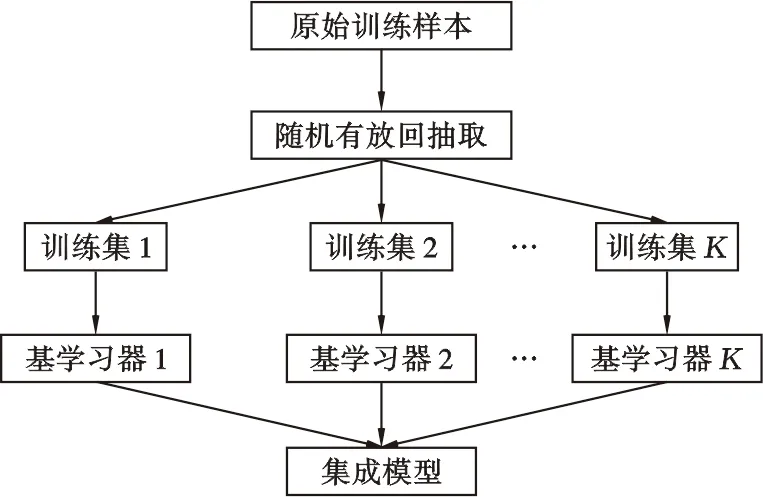
圖2 Bagging算法流程圖

本文評價煤層含氣量的隨機森林回歸模型使用CART樹，隨機森林算法的流程如下：給定原始訓練樣本大小為N，參與建模的特征個數(測井曲線數)為M。

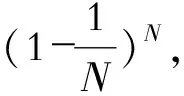
(1)

式(1)中：e為自然常數。可得到當樣本足夠大時，未參與決策樹模型建立的樣本數越趨近于原始訓練樣本數的36.8%，這一部分數據就叫做袋外數據(OOB,out of bag)，一般可用于檢驗決策樹模型效果。

2)基于子訓練集建立決策樹模型，首先從總體特征中隨機選擇m(m≤M)個特征，節點分裂時選取的特征通過計算m個特征的Gini指數。Gini指數越小，代表純度越高，故Gini指數最小的特征即為該節點分裂的最佳特征，Gini指數具體計算公式為：

(2)

式(2)中：pl為樣本屬于第l類的概率；L為目標分裂節點所含樣本的總類別數；A為m個特征中某個特征。通過該公式可以計算得到m個特征中Gini指數最小的特征。而在回歸問題中，通過均方誤差表征純度，均方誤差越小，代表純度越高，故均方誤差最小的特征即為該節點分裂的最佳特征。

通過上述原則，以二叉樹的形式進行分裂至葉子節點，分裂結束的依據由設置的樹的深度以及葉子節點包含最小樣本數所定。

3)重復(1)、(2)步驟K次，即可得到K個子訓練集以及對應的模型，這些相互獨立的模型集成就形成隨機森林模型。

4)利用隨機森林分類模型對測試集進行預測時，每個決策樹模型都會給出一個預測結果。對于回歸類型問題，隨機森林預測結果采取平均值方式，即K個基分類器預測結果的均值為隨機森林預測結果。

可見，隨機森林的“隨機”體現在兩方面：基分類器的訓練數據的隨機性及節點分裂特征選擇的隨機性，因此當基分類器較多時能實現原始訓練數據的有效利用，且Bootstrap的思想能一定程度上解決樣本數據分布不均衡的問題，這也使隨機森林方法成為一種高效且實用性強的非線性算法。

2.2 含氣量原始測試數據采集

針對目標區塊，共收集到38口參數井，對參數井進行了井壁取心，各參數井在3號層采集的巖心樣品個數為6～13組，收集對應參數井測井資料，包括井徑測井、自然伽馬測井、自然電位測井，電阻率系列測井(深、淺側向)與三孔隙度系列測井(補償密度、聲波時差與補償中子)等。以SZN1井為例，展示其含氣量數據來源，該樣品含氣量測定遵照GB/T 19559-2004《煤層氣含量測定方法》。SZN-1井中3號層共采集13個巖心樣本用于解吸實驗，巖心樣本從取心密閉罐中送至實驗室，結合實驗測量了各關鍵參數，最終通過校正得到各井取心樣品在空氣干燥基狀態下的含氣量數值。

2.3 含氣量參數樣本數據庫

1)基于2.2中收集到的目標區塊3號煤層含氣量實驗數據，結合對應巖心樣品的實驗參數值，即實驗室視密度值與實驗室空氣干燥基狀態下的工業組分灰分值，通過比對上述值與實際補償密度測井資料的響應變化趨勢對巖心樣本進行深度歸位。

2)對各參數井間地球物理測井資料進行標準化處理，旨在消除因測井儀器與環境差異導致的測井曲線響應異常，具體做法為將參數井3號煤層上端的致密層視作標準層，以其中一口參數井為標準井，通過對比其他參數井致密層地球物理測井資料響應值與標準井之間的差異，確定加法因子后對地球物理測井資料響應值進行標準化處理，整個工作流程于CIFLOG軟件中完成。

3)對測井資料進行擴徑校正處理，由于煤層機械強度差易碎，使得鉆井過程中易出現井壁垮塌即擴徑現象，這一現象會使得地球物理測井資料響應值出現異常，本文對受擴徑影響嚴重的測井系列進行擴徑校正，利用多元回歸模型完成了三孔隙度系列測井曲線及電阻率測井曲線的擴徑校正。

4)根據深度歸位后巖心樣品的深度段提取對應的地球物理測井資料響應值，由于巖心樣本并非為一深度點而是對應一深度段，因此對測井曲線響應值預處理時結合測井儀器實際采樣間隔進行了多組數據提取以覆蓋整個實驗巖心段，并對樣本數據組進行清洗，清洗目標可分為三類：①深度段對應測井曲線響應不全處，即由于部分巖心樣本位于3號煤層起始段附近與終止段附近，這類樣本點對應的測井曲線響應值往往只有理論響應值的一半(“半幅點”)，不利于后續煤層含氣量模型構建；②夾矸段，在3號煤層下半段中存在非煤巖段，多為泥巖或炭質泥巖，這類巖心樣本對應的地球物理測井資料中自然伽馬測井系列與補償密度測井系列響應值為異常高值，電阻率測井系列響應值為異常低值，故對這類巖心樣本進行清洗；③對本就不符合實驗規范的巖心樣品進行清洗。

綜上，針對目標區塊3號煤層含氣量研究共獲得689組煤層含氣量與測井曲線響應數據用于煤層含氣量模型構建。

2.4 煤層含氣量模型構建與實例效果分析

結合本文實際研究內容，構建目標區塊3號煤層含氣量評價模型的實際步驟為：

1)將實際收集到的地球物理測井曲線響應與煤層含氣量進行相關性分析，已有成果也表明測井曲線與煤層含氣量的變化存在密切關系[5-7]。基于實際測井系列，選取自然伽馬測井曲線，補償密度測井曲線，聲波時差測井曲線，補償中子測井曲線和深、淺側向電阻率曲線為敏感測井曲線，作為特征向量參與建立煤層含氣量評價模型。

2)利用選取出的測井序列按照隨機森林算法建模步驟進行模型構建，通過網格尋優與交叉驗證的方法尋找最優的決策樹個數與分裂特征數，同時測試模型的有效性。

3)根據探究得到的特征個數與回歸子樹個數進行建模，并用未參與建模的數據進行預測驗證，以確保模型的泛化性。

在煤層含氣量模型的構建中，受制于樣本數量的限制，使得這一問題屬小樣本問題，隨機森林算法中對小樣本數據敏感的超參數為決策樹個數與分裂特征數，樹的深度在小樣本數據中作用與決策樹個數差異小，葉子節點數無須參與網格尋優[8]。因此本文對隨機森林中分裂特征數與分裂特征數進行網格尋優，將分裂特征數的尋優步長設為1，決策樹個數尋優步長設置為10，并同時引入交叉驗證用于模型正確性判斷，交叉驗證是指將訓練集數據等分成數份，每次留有一份數據作為驗證，其余數據用于訓練，利用驗證部分的誤差來判斷模型的正確性，最終每一份數據都會得到一份誤差結果，若每一份數據誤差結果差距不大且穩定，則表明方法的正確性與有效性，本文使用的為十折交叉驗證。將現有的樣本數據組中隨機抽取70%的數據作為訓練集，剩余30%的數據作為測試集[18]，訓練集用于訓練構建煤層含氣量模型，測試集用于檢驗煤層含氣量模型的正確性，并在此基礎上，引入同工區中的其他新井作為驗證數據來檢驗模型的泛化性與實用性。首先利用訓練集對模型進行訓練構造，圖3a為隨機森林方法的超參數網格尋優過程，經計算表明，分裂特征數為4且決策樹個數為421時均方誤差最低，并對這一參數配置進行交叉驗證結果檢查，如圖3b所示，結合交叉驗證結果誤差表明，等分的十份數據各作為驗證部分時誤差低且無明顯波動，即構建的模型效果展示無偶然性，也表明了該組超參數尋優結果的正確性。

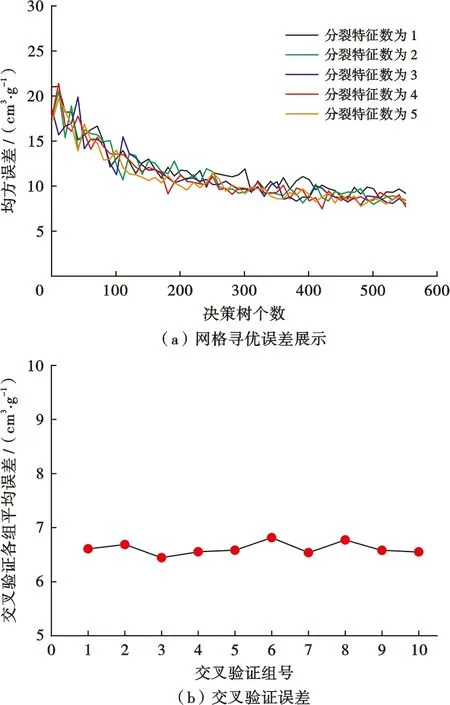
圖3 隨機森林構建煤層含氣量尋優過程

將模型分別應用至測試集與驗證集新井中，效果如圖4所示，圖4a為模型訓練集回判結果，通過繪制交會圖分析得到訓練集數據準確性高，平均相對誤差為4.51%，且所有樣本點均在15%誤差線內；圖4b為模型對數據測試集的應用效果，樣本點中2%的數據落在15%誤差線外，無誤差異常高值點，整體樣本數據均勻分布在零誤差線兩側，平均相對誤差為8.77%；圖4c為對新井數據進行處理后與實驗數據繪制的交會圖，通過誤差分析分析，驗證集數據分布于零誤差線兩側，分析結果表明各組數據相對誤差小于15%，平均相對誤差為9.86%，使用效果與測試集上的表現相吻合。通過上述分析，訓練集的結果表明了模型建立的有效性，表明模型對數據學習利用的完整性，測試集的結果表明了模型的正確性，驗證集的結果表明了模型具有泛化性與實用性。

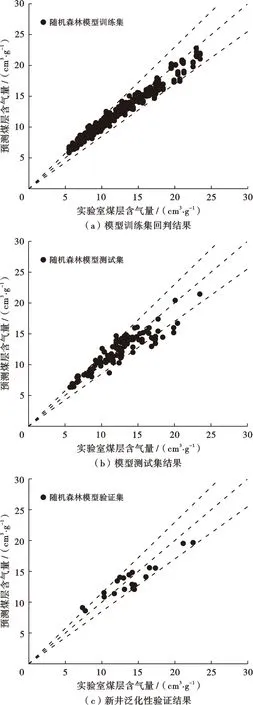
圖4 隨機森林構建煤層含氣量模型效果展示

此外，圖5展示了一口驗證集新井的評價結果，隨機森林方法計算得到的含氣量曲線與對應深度的巖心樣本實驗含氣量結果在數值上吻合程度高。這說明了隨機森林方法在煤層含氣量模型構建的可行性與正確性，也表明了利用隨機森林方法結合地球物理測井資料評價得到的煤層含氣量模型可被推廣應用于煤層含氣量三維精細建模。

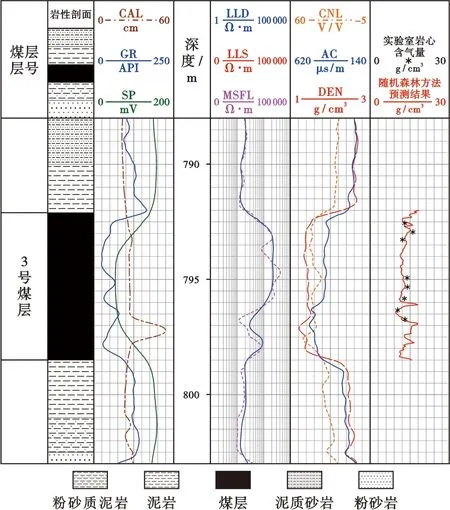
圖5 隨機森林方法構建的煤層含氣量模型在驗證集新井上的應用效果

3 含氣量精細三維模型

煤儲層含氣量三維建模將煤儲層含氣量測試技術、計算機算法和測井學等多門學科有機結合，最大程度精細刻畫含氣量空間分布特征，有效支撐區塊煤層氣滾動勘探和整體開發[19]。

筆者依托參數井巖心含氣量測試數據和隨機森林算法含氣量預測曲線，利用常規油氣成熟三維建模軟件，在3號煤層層序建模的基礎上構建含氣量三維模型，精細刻畫3號煤層含氣量空間分布特征。

3.1 三維地質模型網格設計

依據研究區面積和參與本次建模的煤層氣井平面分布情況，對3號煤層三維地質建模做網格化處理，平面網格設置為100 m×100 m；根據研究區3號煤層厚度大小及穩定性情況，垂向網格控制在0.5 m，三維地質模型的網格為：X方向為111個網格，Y方向為146個網格，Z方向為19個網格，網格總數為111×146×19=307 914個。

3.2 構造模型建立

構造模型是實現煤儲層屬性精細建模的前提。本次研究區勘探開發程度較高，參與此次建模的井數多且分布均勻，為實現精細建模提供資料基礎。將參與建模煤層氣井基礎信息、含氣量測井曲線、煤層頂、底面海拔數據導入，生成3號煤層頂面和底面構造兩個層面，構建煤層結構體和層序建模，實現3號煤層構造建模。結果顯示，山西組3號煤層厚度在2.5～14.0 m，平均6.0 m；區塊具有東西分帶的構造特征，整體呈東南高、西北低的構造格局(圖6)。

圖6 山西組3號煤層三維構造模型

3.3 含氣量屬性建模

在三維構造模型基礎上，利用基于隨機森林算法含氣量預測曲線，構建3號煤層含氣量三維模型。具體步驟為：①將隨機森林算法計算得出的含氣量曲線導入數據庫；②選擇隨機森林算法計算的含氣量曲線，在指定研究區內進行煤層氣井篩選，確定參與建模的煤層氣井和含氣量曲線；③采用序貫高斯算法，利用高斯模型構建含氣量屬性三維模型；④利用變差函數分析對含氣量在空間上的連續性及各方向異性進行評價。模型結果顯示：區內3號煤層含氣量分布在6.4～25.4 m3/t；高含氣區分布在區塊西部和北部，縱向上在距頂面1.0 m和底面2.0 m范圍內發育兩個高含氣層段(圖7)。煤層含氣性對煤層氣勘探開發、儲量評估和產能建設具有決定性指導作用，該模型將對煤層氣精準選區、水平井軌跡設計、射孔層段優選以及低產低效井綜合治理具有重要的指導意義。

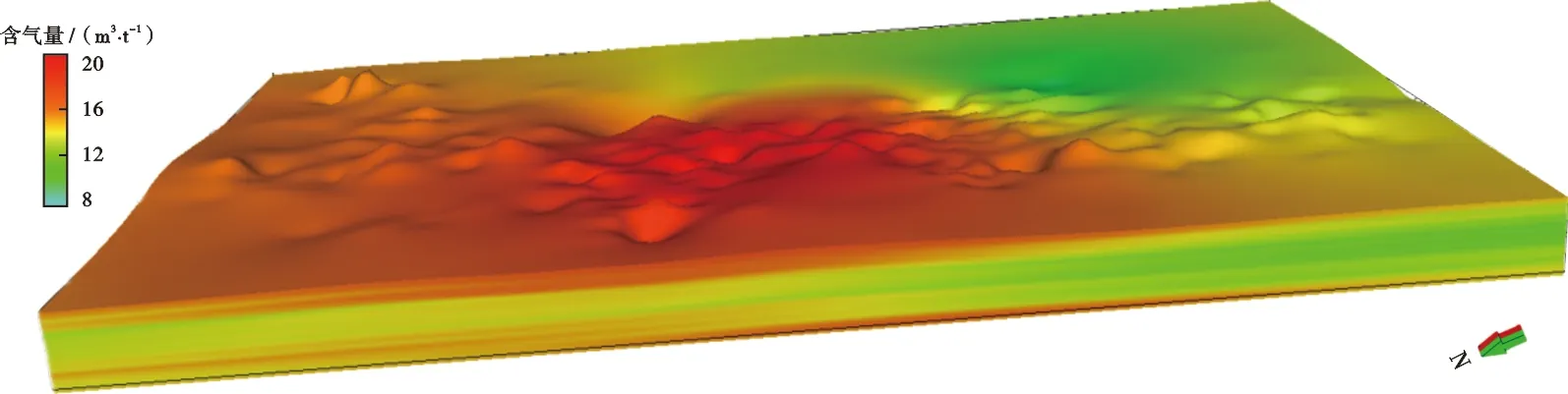
圖7 山西組3號煤層含氣量三維模型

4 結論

1)利用隨機森林方法結合地球物理測井資料可以有效評價煤層含氣量，隨機森林方法因Bagging思想能平衡數據樣本分布不均的問題使得這一模型針對含氣量的評價效果無偏差，且利用網格尋優與交叉驗證相結合的超參數尋優方式能保證模型的正確性與有效性，構建的煤層含氣量模型具有泛化性與實用性，為含氣量精細三維模型的構建打下堅實的數據基礎。

2)機器學習與三維地質建模技術高度融合是實現含氣性空間表征的有效途徑之一。隨機森林算法在含氣量計算中的應用能有效克服樣本數少且非均質性強等問題。對于不同類型煤層氣田適用的機器學習方法會有所不同，需根據具體情況來確定。含氣性空間表征的準確程度取決于含氣量機器學習曲線的數量和參與計算井分布情況，隨著樣本數和參與計算井數的增加以及分布相對均勻，含氣量三維地質模型愈發精確。該方法對于煤層氣精準選區、水平井軌跡設計及鉆探、壓裂射孔優選具有較好指導意義。