強基計劃數學備考系列講座(7)
——集合與函數(下)

王雪芹 王慧興

(1.北京師范大學第二附屬中學 2.清華大學附屬中學)

3.9 方程與不等式

強基校考命題注重考查函數觀點支撐下的解不等式及其應用.

例14(清華大學)定義在R 上的函數f:R→R滿足:f(x3)＝[f(x)]3(?x∈R),f(x1)≠f(x2)(?x1≠x2),則f(0)＋f(－1)＋f(1)的 值是_________.

解析由題設得f(－1)＝[f(－1)]3,f(0)＝[f(0)]3,f(1)＝[f(1)]3,所以f(0),f(－1),f(1)是方程x3－x＝0的三個根,故

例 15(復旦大學)已 知g(x)＝,解不等式0＜g(f(x))＜1.

解析按題意,不等式的解集W?(0,＋∞),所以先作劃分:

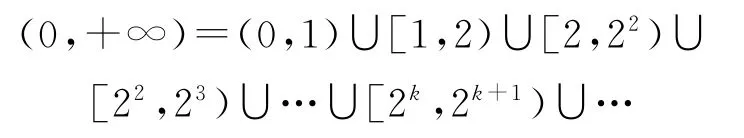
當x∈(0,1)時,f(x)＝log2x＜0,所以[f(x)＋|f(x)|－2]＝－2,且f(x)＋[f(x)]＜0,從而

所以只需f(x)＋[f(x)]＋4＞0,因為h(t)＝t＋[t]＋4(t＝f(x)＜0)不減,而且當時,t＝,則h(－2)＝0,所以滿足g(f(x))＞0的x取值范圍是

任取x∈[2k,2k＋1)(k∈N),則f(x)∈[k,k＋1),[f(x)]＝k,2f(x)－2∈[2k－2,2k),故

當2f(x)－2∈[2k－2,2k－1)時,有[2f(x)－2]＝2k－2,所以所以滿足2f(x)－2＜2k－1的x∈[2k,2k＋1)(k∈N)都不滿足題意.

3.10 復合與迭代

函數復合與迭代運算蘊含遞推等豐富的數學方法,抓住復雜函數關系中的迭代結構,能夠化繁為簡,出奇制勝.

例16解方程

解析把原方程化為

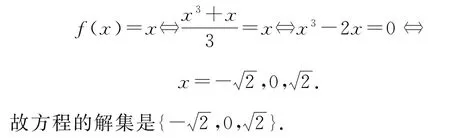
例17(復旦大學)已知函數f(x)＝x2－1,則函數y＝f(f(x))的圖像大致為_________(填圖).

解析由迭代運算y＝f(f(x))＝[f(x)]2－1.如圖4所示,先由函數f(x)＝x2－1的圖像,作出函數y＝|f(x)|的圖像,再作出函數y＝[f(x)]2－1的圖像,經向下平移1個單位即得函數y＝[f(x)]2－1 的圖像,此即復合函數y＝f(f(x))的圖像.

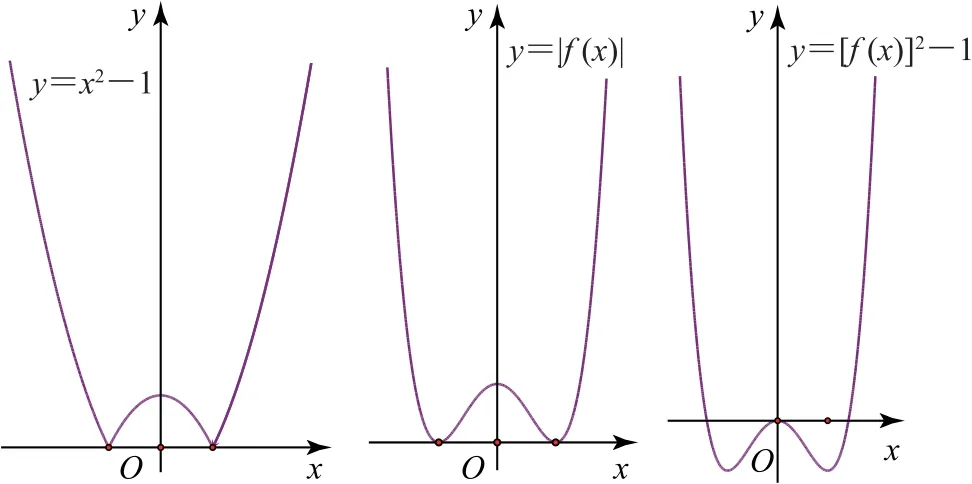
圖4

3.11 最值探究

最值探究包含探求單變量函數最值、多元函數最值以及復合最值,當然,導數是最值探究的重要工具,但我們這里主觀上限制不用導數,注重變形路徑.

例19對一切x∈[a,b],|x2－kx－m|≤1成立,求δ＝b－a的最大值.

解析探究含參數恒成立問題中的參數條件以及帶參數最值都是高校特招試題立意的亮點.

例20(北京大學)對一切x,y＞0,都有5x＋,求實數a的最小值.

對題設不等式調結構——分離參數,得a≥?x,y＞0.

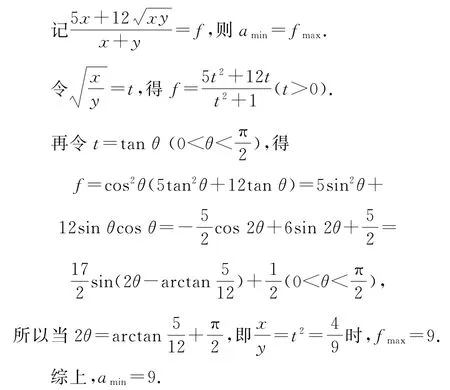
點評本題基于換元和減元,把多元情境轉換為單變量情境,進而應用一元函數求解多元最值.但利用均值不等式求最值,計算過程要簡捷一些.由,得5x＋,等號成立的條件是,故fmax＝9.

例21(上海交大)函數f(x)＝|x2－a|在閉區間[－1,1]上的最大值記作m(a),則m(a)的最小值是_________.

點評本例屬“含參函數復合最值”,另一類形如例22,屬于“多函數復合最值”.

例22(北京大學)求函數f(x)＝max{1－x,

解析,x2}(x∈R)的最小值.

任取x∈R,比較三個數,x2的大小,取其最大的與x相對應,由此建立一個定義在R上的函數,進而利用數形結合思想求其最小值可以分段或畫圖處理,當然也可合理減元、適度放縮求解.

一方面,因為

所以fmin(x)≥1.

另一方面,由f(0)＝max{1,1,0}＝1,可得fmin(x)≤1.

綜上,fmin(x)＝1.

3.12 抽象函數

抽象函數情境能夠有效培育學生數學抽象素養,提升數學理解與綜合分析能力,同時歷練抽象函數問題能為深入分析、求解函數方程做好鋪墊.

例23(北京大學)定義在(－1,1)上的函數f(x)滿足兩個條件:①f(x)＞0,?x∈(－1,0);②,x,y∈(－1,1).則f(x)為( ).

解析?x∈(－1,1),取y＝－x,代入②得

在②中,取x＝y＝0,得f(0)＝0,代入③,得f(－x)＝－f(x),?x∈(－1,1),故f(x)是奇函數,選項A 正確,結合條件①可知選項B不正確.

?x∈(0,1),有－x∈(－1,0),所以

任取－1＜x1＜x2＜1,代入條件②,得

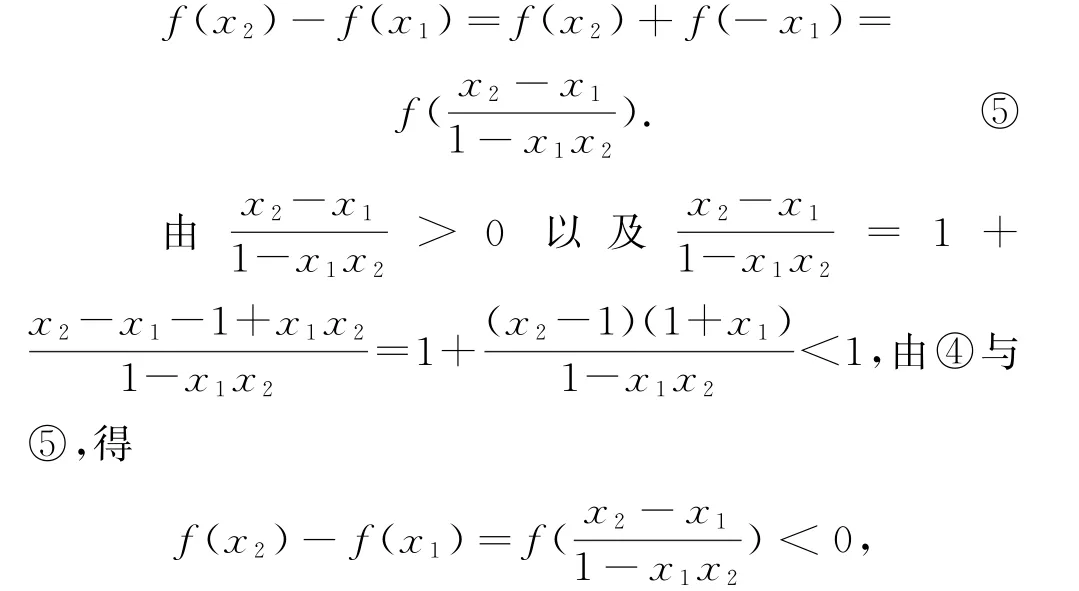
即f(x2)＜f(x1),故f(x)是減函數,選項C正確,B不正確.

綜上,選AC.

3.13 函數方程

在強基計劃數學測試中,立意柯西方程及其變式的函數方程問題比較常見.

例24求所有函數f:Z→Z,使得?a,b∈Z,都有f(2a)＋2f(b)＝f(f(a＋b)).

解析f(x)＝0是平凡解,以下設f(x)不為常數.因為

令F(x)＝f(x)－f(0),則式③可以轉化為如下柯西方程:

代入題設函數方程得

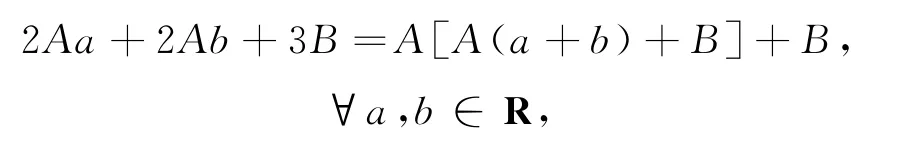
綜上,f(x)＝0(x∈Z)或f(x)＝2x＋B(x∈Z),其中B是任一整數.

例25(清華大學)給定a∈R,函數f:R→R 滿足,f(x＋y)＝f(x)f(a－y)＋f(y)f(a－x)(?x,y∈R),則( ).

解析在題設函數方程中,取x＝y＝0,由f(0)＝,得f(0)＝f(0)f(a)＋f(0)f(a)＝f(a),所以選項A 正確.

在題設函數方程中,取y＝0,?x∈R,得

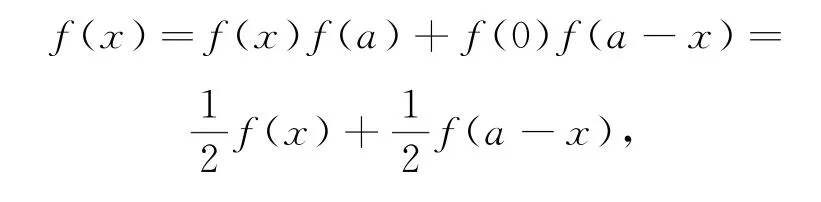
所以f(a－x)＝f(x)(?x∈R),則題設函數方程為

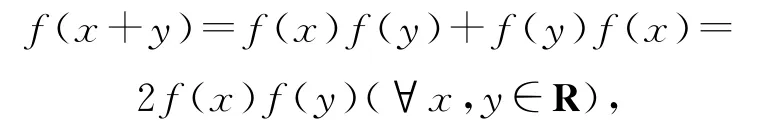
故選項C正確.

任取x∈R,以分別替換題設函數方程中的x,y,得

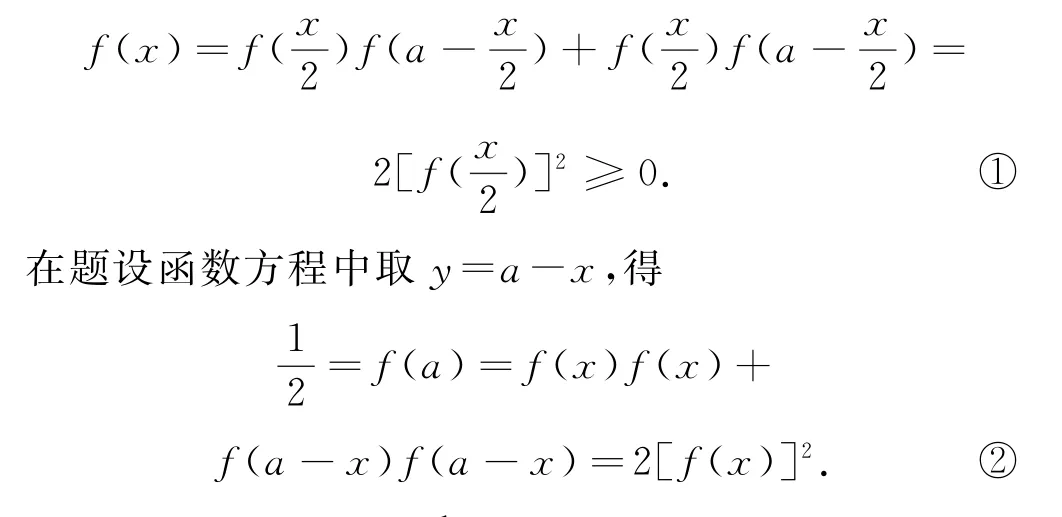
綜上,故選ABC.

點評由已得等式f(x＋y)＝2f(x)f(y)(?x,y∈R),得,則,從而(?x∈R).進而可以化為柯西方程

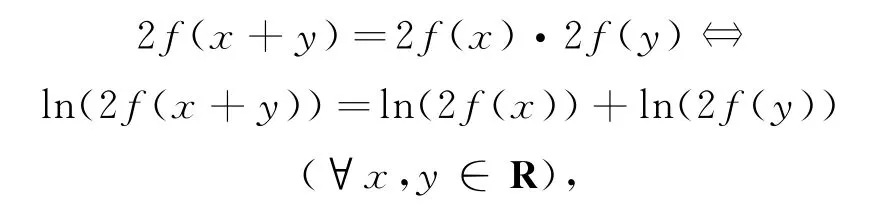
令ln(2f(x))＝g(x)(x∈R),得g:R→R 滿足柯西方程g(x＋y)＝g(x)＋g(y)(x,y∈R),由柯西方程得其連續解g(x)＝kx,所以,其中常數c＝g(1)＝ln(2f(1)).

但已得到的性質f(a－x)＝f(x)(?x∈R),表明函數f:R→R的圖像關于直線對稱,所以必有c＝1,即

遺憾的是命題者可能是受學生常態知識所限,沒有給出連續性條件,這樣應用柯西方程就不夠嚴謹.

例26(中國科學技術大學)求所有函數f:R→R,使得對一切x,y∈R都有

解析按題意,有f(0)＝f(f(x)－f(x))＝f(f(x))＋2f(x)f(x)＋f(f(x))－1＝2f(f(x))＋2[f(x)]2－1,所以

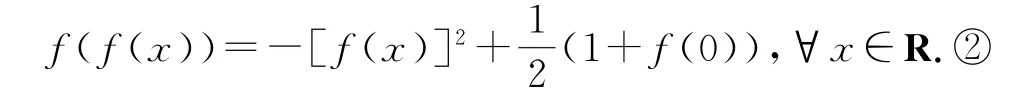
再由①和②,可得?x,y∈R,都有

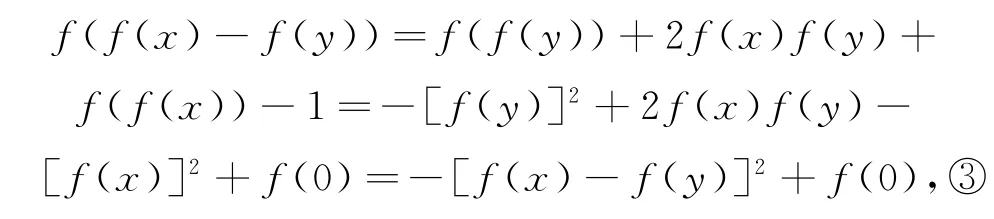
再由①,可得f(x－f(y))－f(x)＋1＝2xf(y)＋f(f(y)),所以?x,y∈R,都有

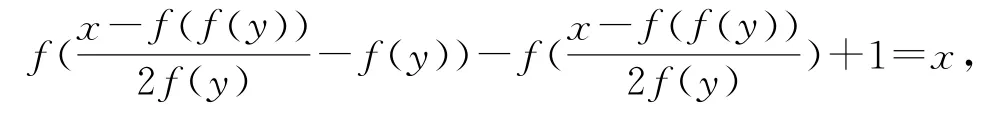
故?x∈R,都存在u,v∈R,使得x＝f(u)－f(v)＋1,故對一切u,v∈R,有

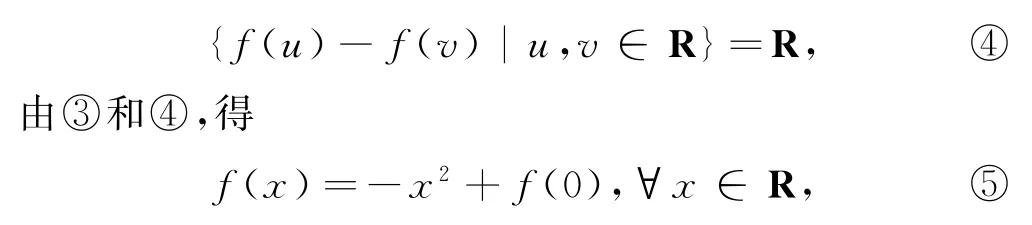
代回式①,得?x,y∈R,都有

所以,滿足題設條件的函數f:R→R為f(x)＝1－x2(x∈R).

點評本例體現求解函數方程的基本方法——替換、減元、對稱、同構、任意性、必要性與充分性.

3.14 綜合應用

強基校考重視函數應用,應用型函數問題多種多樣,多以處理帶參數不等關系問題表現函數應用.

例27(中國科學技術大學)若函數f(x)＝(x－1)2＋k2,并且?a,b,c∈(0,1),都存在以f(a),f(b),f(c)為邊的三角形,求k的范圍.

解析把定義域拓展到[0,1],按題意,其等價條件是2k2＝2f(1)＝2fmin(x)≥fmax(x)＝f(0)＝1＋k2?k2≥1?k≤－1或k≥1,故實數k的取值范圍是(－∞,－1]∪[1,＋∞).

例28(復旦大學)給定5個函數,其中3個奇函數,2個偶函數,則在這5個函數中任意取3個,其中既有奇函數又有偶函數的概率是.

4 實戰演練

1.(上海交通大學)若集合M中任意兩個元素的和、差、積、商(分母不為零)都還在M內,則稱集合M是封閉的.在集合R,Q,?RQ,n∈Z中,封閉的集合個數是_________.

2.(上海交通大學)已知集合M＝{(x,y)|x(x－1)≤y(1－y)},N＝{(x,y)|x2＋y2≤k}滿足M?N,則實數k的最小值是_________.

3.(浙江大學)設M＝{x∈R|f(x)＝x},N＝{x∈R|f(f(x))＝x}.

(1)求證:M?N;

(2)當f:R→R 是增函數,是否有M＝N? 證明你的結論.

4.(上海交通大學)已知二次函數f(x)＝ax2＋bx＋c(a≠0)沒有不動點,則它是否有穩定點? 證明你的結論.

5.(上海交通大學)證明:若f(f(x))有唯一不動點,則f(x)也有唯一不動點.

6.(上海交通大學)求集合A＝{a1,a2,…,an}?N*(n≥2),滿足a1＋a2＋…＋an＝a1·a2·…·an.

7.(復旦大學)命題p:“△ABC的內心與外心重合”是命題q:“△ABC是正三角形”的什么條件?

8.(清華大學)《紅樓夢》《三國演義》《水滸傳》和《西游記》四部書陳列在四層架子書柜的不同層上,小趙、小錢、小孫、小李分別借閱了四部書中的一部.現已知:小錢借閱了第一層的書籍,小趙借閱了第二層的書籍,小孫借閱的是《紅樓夢》,《三國演義》在第四層,則( ).

A.《水滸傳》一定陳列在第二層

B.《西游記》一定陳列在第一層

C.小孫借閱的一定是第三層上的書籍

D.小李借閱的一定是第四層上的書籍

9.(上海交通大學)設常數c∈(0,1),函數f(x)的定義域為(0,1),則函數g(x)＝f(x＋c)＋f(xc)的定義域為________.

10.(清華大學)給定三次函數p(x)＝x3－3x＋1.

(1)證明:函數p(x)有三個零點a＜b＜c;

(2)證明:若x＝t是p(x)的一個零點,則x＝t2－2也是p(x)的一個零點;

(3)定義映射f:{a,b,c}→{a,b,c},x|→x2－2,求f(a),f(b),f(c).

11.設x,y∈R.

(1)若x,y∈(－2,1),求證:2(x2＋xy＋y2)＋3xy＜12;

(2)求證:x2＋xy＋y2＋3(x＋y)＋6＞0;

(3)求證:x2＋xy＋y2－3(x＋y)＋3≥0.

12.(南京大學)已知0≤a＋b,b＋c,c＋a≤1,求的最值.

13.(中國科學技術大學)已知a＞0,二次函數f(x)＝ax2－x＋1,若在任意長度為1的區間上,存在兩點函數值之差不小于1,則a的最小值為_________.

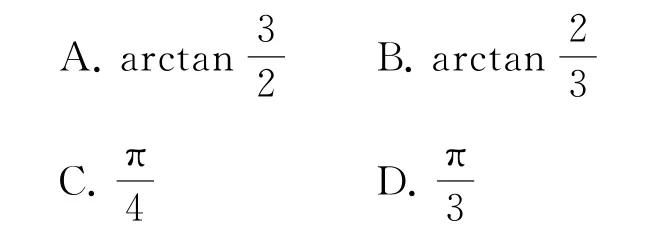
15.(上海交通大學)已知方程2x－sinx＝1,則下列判斷:

①方程沒有正數解;

②方程有無窮多個解;

③方程有一個正數解;

④方程的實根小于1.

其中錯誤的判斷有________.

A.f(x,y,z)既有最大值也有最小值

B.f(x,y,z)有最大值但無最小值

C.f(x,y,z)有最小值但無最大值

D.前三個答案都不對

A.1 B.2 C.3 D.前三個答案都不對

18.(中國科學技術大學)求所有a∈R,使得f(x)＝x3＋ax2－x＋1－a,滿足|f(x)|≥|x|,?x∈[－1,1].

19.(南京大學)求函數f:R→R,使得f(f(x＋y))＝f(x＋y)＋f(x)f(y)－xy(?x,y∈R).

20.設實數a,b,c＞0,若一元二次方程ax2＋bx＋c＝0有實根,則( ).

(完)