從2022年高考試題再看函數圖像的雙對稱問題
孫丕訓(特級教師) 王麗君
(北京陳經綸中學)
函數的性質是高中數學重要的學習內容,也是高考的必考內容.函數的對稱性是函數的重要性質,也是高考的考查熱點.從歷年高考試題來看,對函數對稱性的考查,題目越來越新穎,對思維能力的要求也越來越高.在2022年新高考Ⅰ卷和全國乙卷中,選擇題的最后一題都是函數對稱性問題,而這兩道題都可以轉化成函數圖像的雙對稱問題(即函數圖像關于兩條直線對稱,或關于兩個點對稱,或關于一條直線及一個點對稱).
首先,關于函數圖像的對稱性,有性質1、性質2.
性質1如果對于函數f(x)在定義域R 內的任意一個x,都有f(a+x)=f(a-x),則函數f(x)的圖像關于直線x=a對稱;反之,若函數f(x)的圖像關于直線x=a對稱,則有f(a+x)=f(a-x)(如圖1).
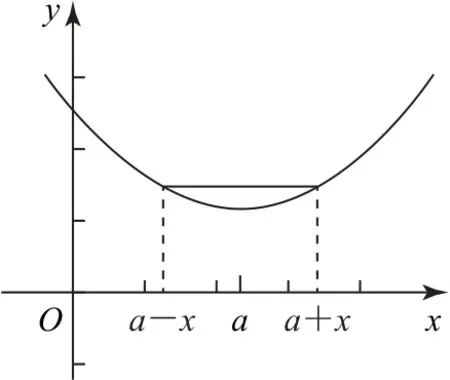
圖1
特別地,當a=0時,函數f(x)為偶函數.
性質2如果對于函數f(x)在定義域R內的任意一個x,都有f(a+x)+f(a-x)=2b,則函數f(x)的圖像關于點(a,b)對稱;反之,若函數f(x)的圖像關于點(a,b)對稱,則有f(a+x)+f(a-x)=2b(如圖2).
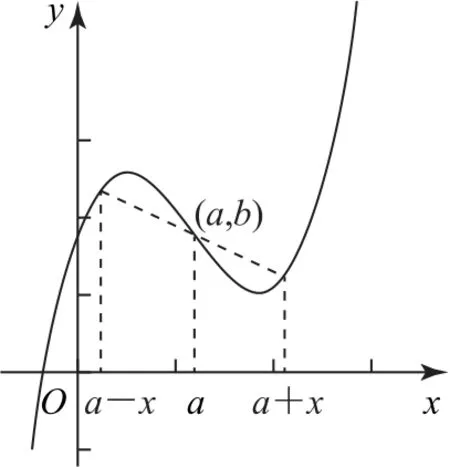
圖2
特別地,當a=0,b=0時,函數f(x)為奇函數.
函數圖像的雙對稱問題,往往隱含著周期性,如性質3、性質4、性質5.
性質3如果函數f(x)的定義域為R,且函數f(x)的圖像既關于直線x=a對稱,又關于直線x=b對稱(a≠b),那么函數f(x)必為周期函數,其中一個周期為
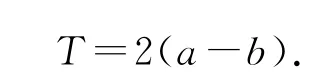
證明因為函數f(x)的圖像關于直線x=a對稱,所以f(a+x)=f(a-x),即
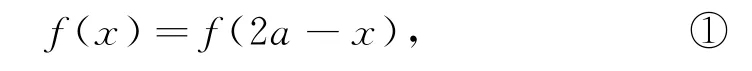
又因為f(x)的圖像關于直線x=b對稱,所以f(b+x)=f(b-x),即
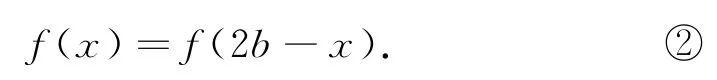
由①和②得f(2a-x)=f(2b-x),將x換為2bx,則f(x+2a-2b)=f(x),所以f(x)為周期函數,其中一個周期為T=2(a-b).
性質4如果函數f(x)的定義域為R,且函數f(x)的圖像既關于點(a,t)對稱,又關于點(b,t)對稱(a≠b),那么函數f(x)必為周期函數,其中一個周期為T=2(a-b).
證明過程與性質3類似,在此不再贅述.
性質5如果函數f(x)的定義域為R,且函數f(x)的圖像既關于直線x=a對稱,又關于點(b,t)(a≠b)對稱,那么函數f(x)必為周期函數,其中一個周期為T=4(a-b).
證明因為函數f(x)的圖像關于直線x=a對稱,所以f(a+x)=f(a-x),即
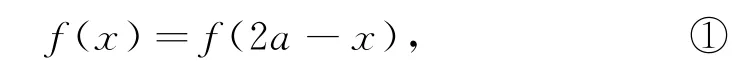
又因為函數f(x)的圖像關于點(b,t)(a≠b)對稱,所以f(b+x)+f(b-x)=2t,即
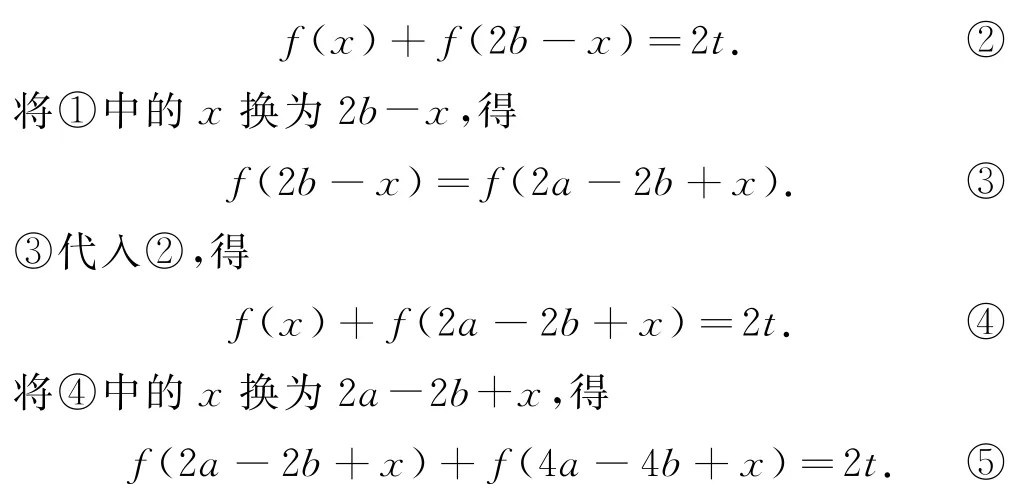
由④和⑤得f(x)=f(4a-4b+x),所以函數f(x)為周期函數,其中一個周期為T=4(a-b).
下面我們應用以上性質解決2022年高考中選擇題的壓軸題.
例1(2022年新高考Ⅰ卷12,多選題)已知函數f(x)及其導函數f′(x)的定義域為R,記g(x)=f′(x).若,g(2+x)均為偶函數,則( ).
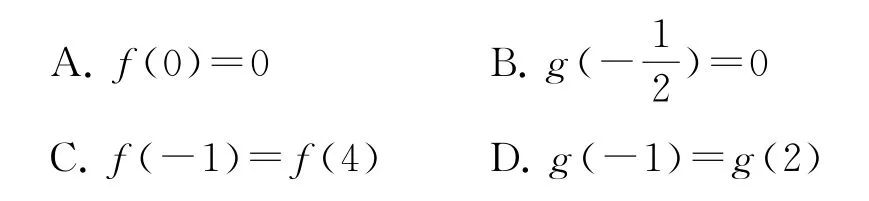
由g(2+x)為偶函數得g(2+x)=g(2-x),所以g(x)關于直線x=2對稱.
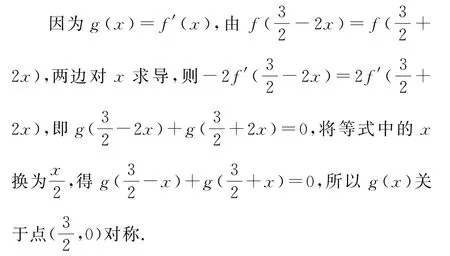
由性質5,可知函數g(x)的一個周期為
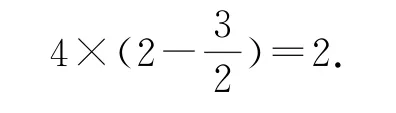
由g(2+x)為偶函數,則g(2+x)=g(2-x),所以f′(2+x)=f′(2-x),即(f(2+x)+f(2-x))′=0,所以f(2+x)+f(2-x)=t(t為常數),所以f(x)關于點對稱.同理可得,函數f(x)的一個周期為
綜上,函數f(x)與g(x)均是周期為2的周期函數,所以,常數t可取任意實數,A不正確.另外,對于選項A 的排除,也可根據已知條件知:若函數f(x)滿足已知條件,則函數f(x)+C(C為常數)也滿足條件,所以無法確定f(0),故A 不正確.

綜上,故選BC.
不可否認,傳統報紙在讀者的心中權威性很高,得到大家的一致認可,現在雖然我們利用網絡能夠獲得各種各樣的新聞,但是網上新聞的質量參差不齊,有好有壞,碎片化的現象非常明顯。而且,有時候為了博得人們眼球,會散布虛假信息。報紙可以和互聯網結合起來,找到切入點,尋找適合報紙刊登的新聞選題,不斷挖掘新聞的價值,利用報紙媒體優勢圍繞選題進行全方位的報道,利用報紙媒體的影響力優化網絡上的熱門話題,不斷擴展報紙媒體的空間,讓報紙媒體和互聯網共贏。
點評求解本題的關鍵是通過g(x)=f′(x)的關系,對關于f(x)的等式兩邊求導、對g(x)的等式積分(導數的逆運算),得到f(x)與g(x)的另一組體現對稱性的關系式,進而得出函數的周期性,從而解決問題.
本題為多選題,正確的選項需推理得到,錯誤的選項可用排除法.在得到g(-1)+g(2)=0時,并不能排除選項D,這是因為當g(-1)=g(2)=0時,D仍可能正確,要排除D,需說明g(-1)不一定為0,根據函數f(x)的對稱性,不難舉出滿足條件的一個函數f(x)=sinπx,此時,g(-1)≠g(2),故排除選項D.另外,f(x)=sinπx+C(C為常數)均符合條件,可迅速排除A 和D.
例2(2022年全國乙卷理12)已知函數f(x),g(x)的定義域均為R,且f(x)+g(2-x)=5,g(x)-f(x-4)=7,若y=g(x)的圖像關于直線x=2對稱,g(2)=4,則

解析因為g(x)關于直線x=2對稱,所以g(2+x)=g(2-x).因為
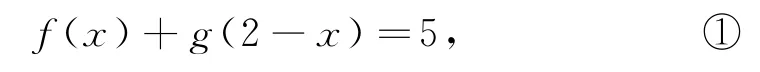
將①中的x換成-x,得
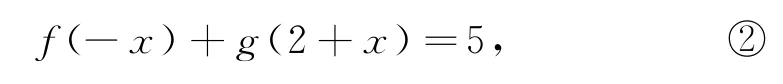
①-②,得f(x)=f(-x),即f(x)為偶函數,f(x)關于直線x=0對稱;在g(x)-f(x-4)=7中,將x換成x+2,得
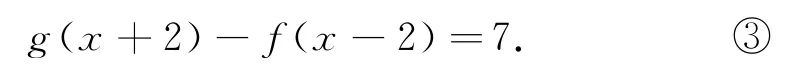
②-③,得f(-x)+f(x-2)=-2,即f(x)關于點(-1,-1)對稱,應用性質5,f(x)的一個周期為4.
在式①中,令x=0,得f(0)+g(2)=5,又因為g(2)=4,所以f(0)=1,在f(-x)+f(x-2)=-2中,令x=1,則f(-1)=-1,再由f(x)=f(-x),可得f(1)=f(-1)=-1,因為f(x)的周期為4,所以f(2)=f(-2)=-2-f(0)=-3,f(3)=f(-1)=-1,f(4)=f(0)=1,所以
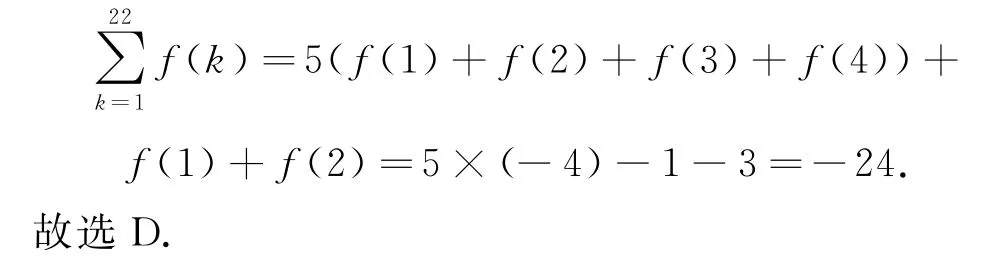
點評求解本題的關鍵是利用方程的思想,由g(2+x)=g(2-x)這個關系式,結合已知條件中的兩個等式,運用消元法得到f(x)的對稱軸和對稱中心,進而得出函數的周期,問題得以解決.
函數圖像的雙對稱性質能得出函數的周期性,把握這個本質在解決問題過程中能起到事半功倍的作用.最后,給出4個練習,均選自近幾年高考真題,都是抽象函數的雙對稱問題,題干簡潔,內容豐富,讀者可以利用以上性質試一試.
鏈接練習
1.(2021年新高考Ⅱ卷8)已知函數f(x)的定義域為R,f(x+2)為偶函數,f(2x+1)為奇函數,則( ).
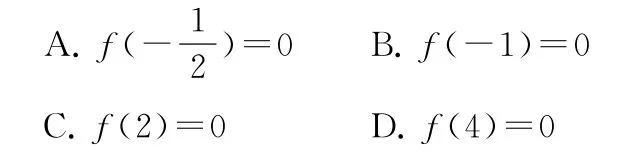
2.(2021 年全國甲卷理12)設函數f(x)的定義域為R,f(x+1)為奇函數,f(x+2)為偶函數,當x∈[1,2]時,f(x)=ax2+b,若f(0)+f(3)=6,則
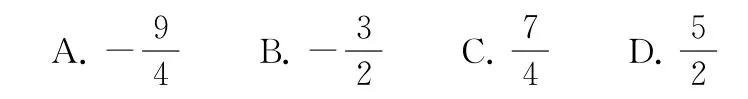
3.(2021年全國甲卷文12)設f(x)是定義域為R 的奇函數,且f(1+x)=f(-x).若
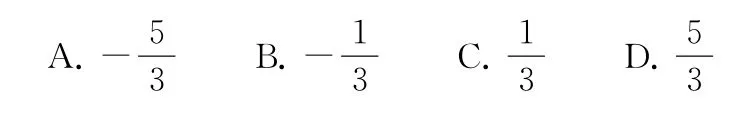
4.(2018年全國Ⅱ卷理11)已知f(x)是定義域為(-∞,+∞)的奇函數,滿足f(1-x)=f(1+x).若f(1)=2,則f(1)+f(2)+f(3)+…+f(50)=( ).
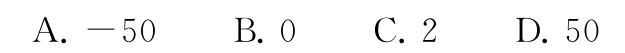
鏈接練習參考答案
1.B. 2.D. 3.C. 4.C.
(完)

