利用構造函數法求解導數不等式問題

魏立向

(甘肅省定西市安定區交通路中學)

不等式求解問題是高考的重點內容,利用函數單調性證明不等式問題是近幾年高考的熱點和難點.若在一個不等式中同時含有f(x)與f′(x),常通過構造輔助函數來求解,即構造一個含有f(x)與另一函數g(x)的積或商的新函數F(x)來解題.

根據函數的求導法則,構造輔助函數經常要用到以下幾種常見的數學模型.

構造差函數對于不等式f′(x)－g′(x)≥0,構造函數F(x)＝f(x)－g(x).特別地,對于不等式f′(x)≥k,構造函數F(x)＝f(x)－kx.

構造積函數1)對于不等式f′(x)g(x)＋f(x)g′(x)≥0,構造函數F(x)＝f(x)g(x).

2)對于不等式xf′(x)＋nf(x)≥0,構造函數F(x)＝xnf(x).

3)對于不等式f′(x)＋f(x)≥0,構造函數F(x)＝exf(x).

4)對于不等式f′(x)＋kf(x)≥0,構造函數F(x)＝ekxf(x).

構造商函數1)對于不等式f′(x)g(x)－f(x)g′(x)≥0,構造函數,則

1 構造差函數F(x)=f(x)-g(x)

例1已知函數f(x)為R上的偶函數,f′(x)是f(x)的導函數,且當x∈[0,＋∞)時,f′(x)＞2x.若f(a－1)－f(a)≥1－2a,求實數a的取值范圍.

令F(x)＝f(x)－x2,因為f(x)為R 上的偶函數,所以F(x)為R 上的偶函數,且F′(x)＝f′(x)－2x.又因為當x∈[0,＋∞)時,F′(x)＝f′(x)－2x＞0,所以F(x)在[0,＋∞)上是增函數.又因為F(x)為R 上的偶函數,所以F(x)在(－∞,0)上是減函數.

f(a－1)－f(a)≥1－2a等價于f(a－1)－1＋2a－a2≥f(a)－a2,即f(a－1)－(a－1)2≥f(a)－a2,則F(a－1)≥F(a),所以|a－1|≥|a|,解得a≤,故a的取值范圍是

2 構造積函數F(x)=xnf(x)

例2已知y＝f(x)是定義在R上的奇函數,且當x＜0時,不等式f(x)＋xf′(x)＜0成立,若a＝20.3·f(20.3),b＝logπ3·f(logπ3),,試判斷a,b,c的大小關系.

設F(x)＝xf(x),則F′(x)＝f(x)＋xf′(x),結合已知可得當x＜0時,F′(x)＜0,故F(x)在(－∞,0)上單調遞減.

由y＝f(x)為R 上的奇函數知F(x)＝xf(x)為R上的偶函數,所以F(x)在(0,＋∞)上單調遞增,所以

又0＜logπ3＜1＜20.3＜3,所 以F(logπ3)＜F(20.3)＜F(3),即b＜a＜c.

3 構造商函數

例3已知函數f(x)是定義在(－∞,0)∪(0,＋∞)上的偶函數,f′(x)是函數f(x)的導函數,若?x＞0,都有xf′(x)－2f(x)＞0 成立,試比較9f(－2)與4f(3)的大小.

又因為函數f(x)是定義在(－∞,0)∪(0,＋∞)上的偶函數,則F(x)為(－∞,0)∪(0,＋∞)上的偶函數,故F(－2)＝F(2),結合F(2)＜F(3),則F(－2)＜F(3),故即9f(－2)＜4f(3).

4 取對數法構造形似函數

例4求證:當m＞n＞0時,有(e＋m)e＋n＜(e＋n)e＋m成立.

證明當m＞n＞0時,要證不等式(e＋m)e＋n＜(e＋n)e＋m成立,只需證(e＋n)ln(e＋m)＜(e＋m)·ln(e＋n)成立,即證成立.

5 移項法構造二階導函數

例5已知函數f(x)＝2aex－x2.

(1)若f(x)為R 上的增函數,求實數a的取值范圍;

(2)若a＝1,求證:?x＞0,f(x)＞2x＋2成立.

(1)由f(x)＝2aex－x2(x∈R),得f′(x)＝2aex－2x(x∈R),因為f(x)為R 上的增函數,所以f′(x)≥0在R上恒成立,即2aex－2x≥0在R上恒成立,即

綜上,a的取值范圍是

(2)當a＝1,x＞0時,f(x)＝2ex－x2(x＞0),要證當a＝1 時,?x＞0,f(x)＞2x＋2 成立,只需證f(x)－(2x＋2)＞0(x＞0)恒成立,即證2ex－x2－2x－2＞0(x＞0)恒成立.

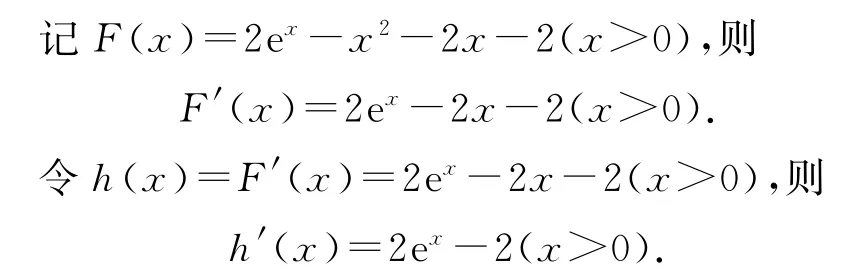
顯然,當x＞0時,h′(x)＞0,h(x)在(0,＋∞)上單調遞增.又h(x)在x＝0處連續,h(x)＞h(0)＝0,即F′(x)＞0,F(x)在(0,＋∞)上單調遞增.

又F(x)在x＝0處連續,F(x)＞F(0)＝0,即

綜上,當a＝1時,?x＞0,f(x)＞2x＋2成立.

總而言之,利用構造函數法求解導數不等式問題的關鍵在于充分挖掘題中的條件,構造合適的輔助函數,與題設形成解題鏈條,再將不等式的求解問題轉化為研究輔助函數的單調性和最值問題,進而可解原不等式.

鏈接練習

1.定義在R 上的函數f(x)滿足f′(x)＋f(x)＞1,f(0)＝3,則不等式exf(x)＞ex＋2的解集為( ).

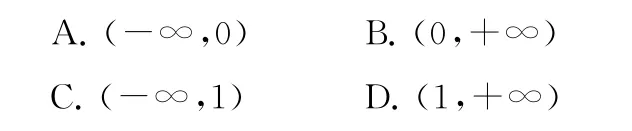
2.定義在R 上的函數f(x)滿足f(1)＝2,且對任意的x∈R有f′(x)＜1,則不等式f(x2)＞x2＋1的解集是( ).

3.設f′(x)是奇函數f(x)(x∈R)的導函數,且f(2)＝0,當x＞0時,xf′(x)－f(x)＜0,使得f(x)＞0成立的x的取值范圍是( ).

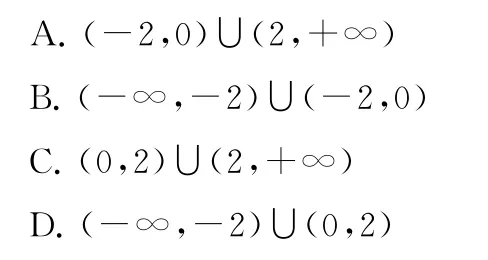
鏈接練習參考答案

1.B. 2.C. 3.D.

(完)